直线和平面垂直的判定
图片预览




文档简介
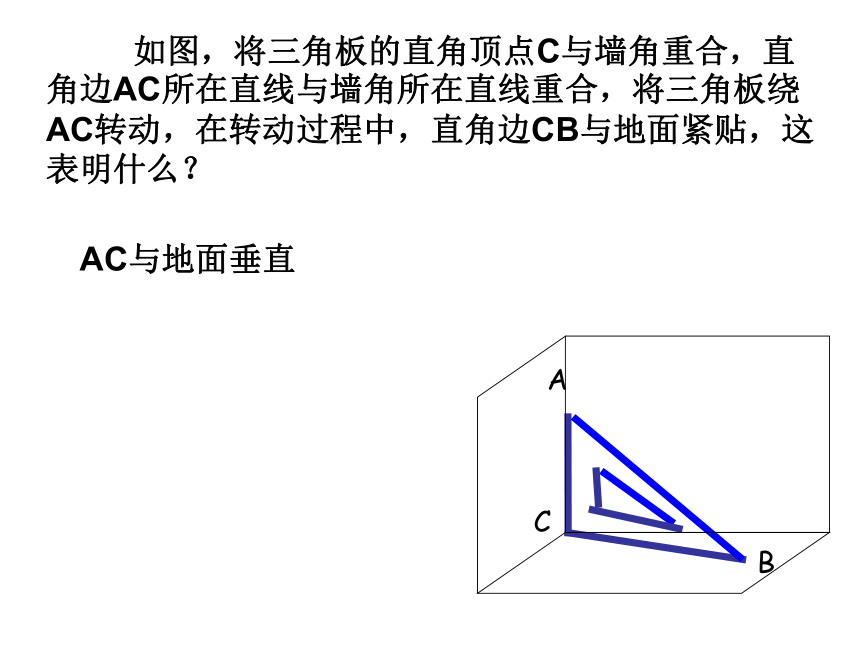
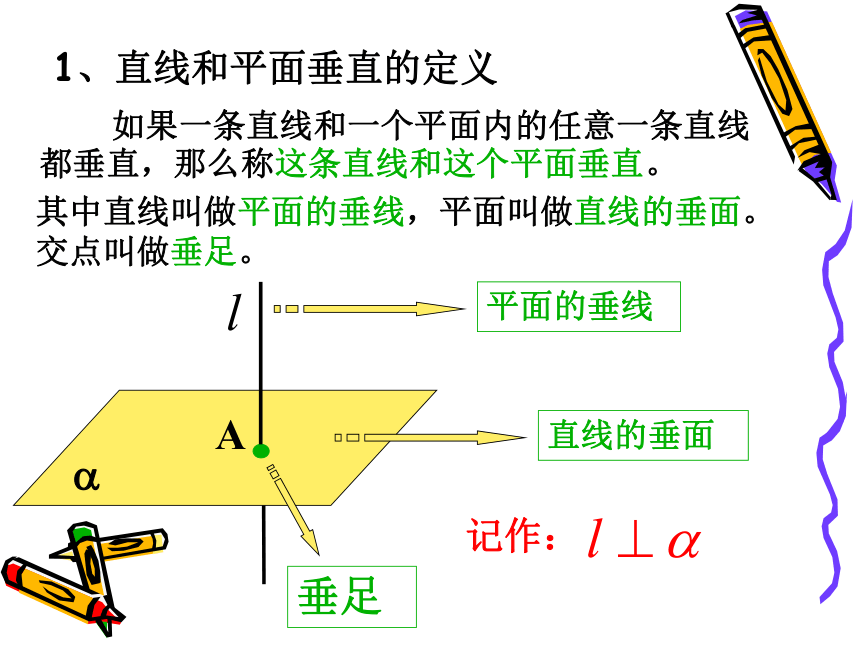
课件21张PPT。直线与平面垂直的判定大漠孤烟直ABC 如图,将三角板的直角顶点C与墙角重合,直角边AC所在直线与墙角所在直线重合,将三角板绕AC转动,在转动过程中,直角边CB与地面紧贴,这表明什么?AC与地面垂直1、直线和平面垂直的定义 如果一条直线和一个平面内的任意一条直线
都垂直,那么称这条直线和这个平面垂直。平面的垂线直线的垂面垂足其中直线叫做平面的垂线,平面叫做直线的垂面。
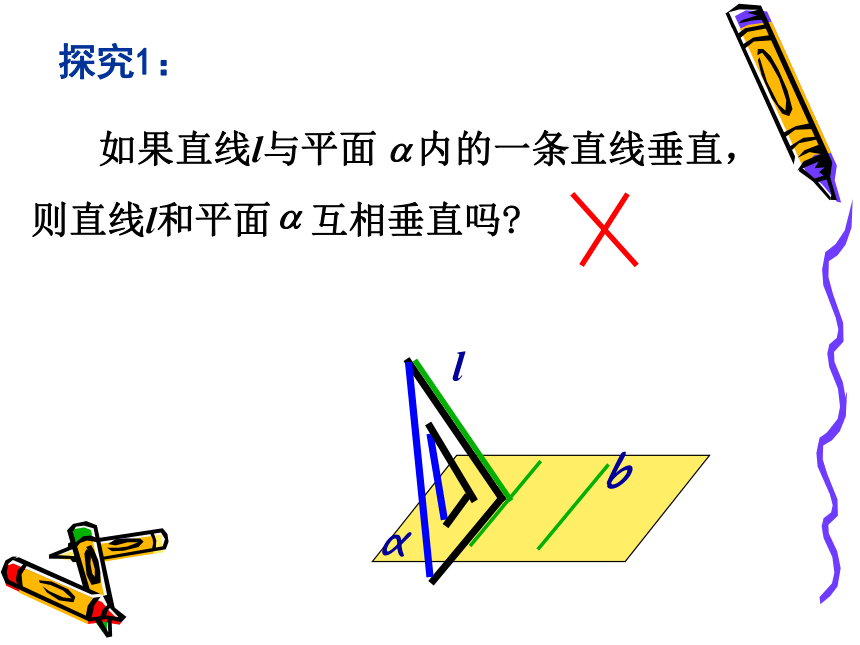
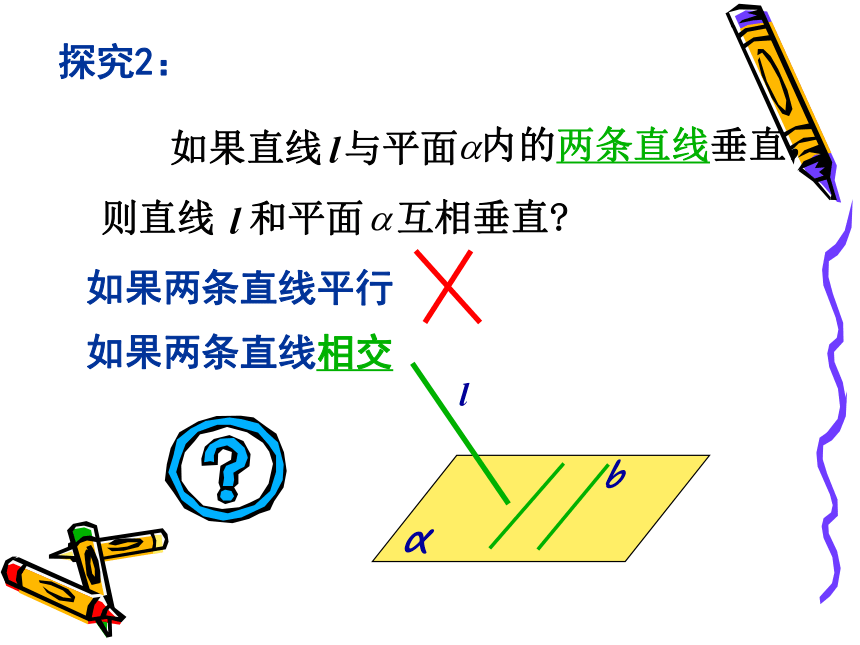
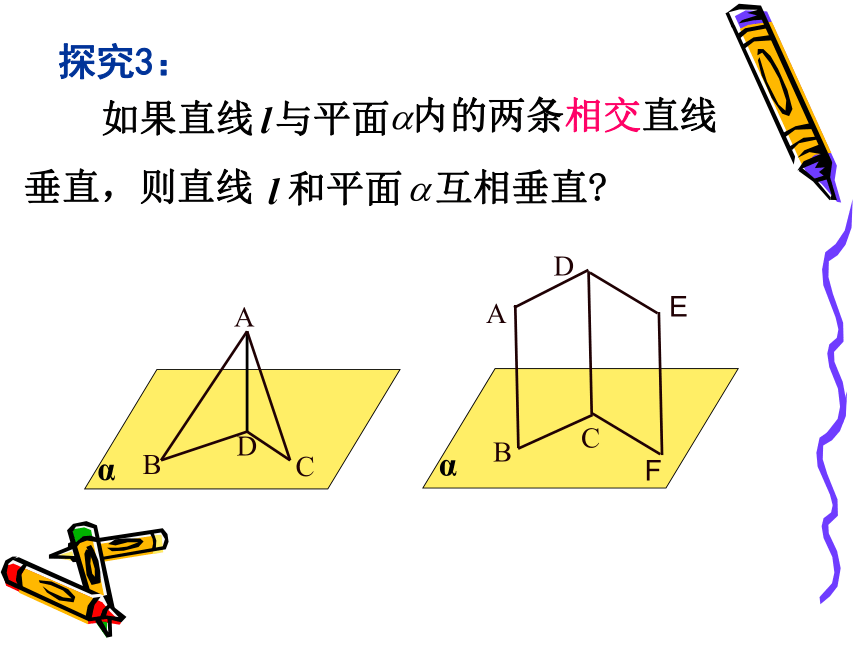
交点叫做垂足。显然用定义一般是不可行的.是否有简单实用的判定方法,下来我们探究一下如何判定一条直线与一个平面垂直呢?探究1:探究2:如果两条直线平行如果两条直线相交探究3:探究3:l如果直线与平面内的两条相交直线垂直,则直线l和平面互相垂直?再比如,观察以下长方体,易知:
直线a不在平面 内,直线b,c在平面 内,
b ∥c这时,a与 不垂直abc如果一条直线和一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 关键:线不在多 相交则行2、直线与平面垂直的判定定理符号表示:线面垂直的画法通常把表示直线的线段画成和表示平面的平行四边形的横边垂直(4)如果一条直线垂直于平面内的无数条直线,
那么这条直线垂直这个平面 ( )( )( )练习1:判断题
(5)如果一条直线垂直于平面内的任意两条直线,
那么这条直线垂直这个平面 ( )( )( )练习1:判断题
(6)如果一条直线垂直于平面内的两条相交直线,
那么这条直线垂直这个平面 ( )(7)过一点引已知平面的垂线有且仅有一条(8)过一点引已知直线的垂面有且仅有一条( )例1:如图所示,PA⊥平面ABC,BC⊥AB,
写出图中所有的直角三角形;解:图中共有四个直角三角形。Rt△ABC
Rt△PAB
Rt△PAC
Rt△PBC线面垂直的定义 线面垂直的判定定理线线垂直线面垂直关键:线不在多 相交则行线面垂直的定义3、课堂小结作业练习2: 如图: 在空间四边形ABCD中,
AB = AD, CB = CD,
求证: AC BD
证明:取 BD 中点E因为 AB=AD,E 是 BD 的中点
所以 AE BD 同理 EC BD 所以 BD 平面AEC 因为 AC 在平面AEC内所以 AC BDE
都垂直,那么称这条直线和这个平面垂直。平面的垂线直线的垂面垂足其中直线叫做平面的垂线,平面叫做直线的垂面。
交点叫做垂足。显然用定义一般是不可行的.是否有简单实用的判定方法,下来我们探究一下如何判定一条直线与一个平面垂直呢?探究1:探究2:如果两条直线平行如果两条直线相交探究3:探究3:l如果直线与平面内的两条相交直线垂直,则直线l和平面互相垂直?再比如,观察以下长方体,易知:
直线a不在平面 内,直线b,c在平面 内,
b ∥c这时,a与 不垂直abc如果一条直线和一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 关键:线不在多 相交则行2、直线与平面垂直的判定定理符号表示:线面垂直的画法通常把表示直线的线段画成和表示平面的平行四边形的横边垂直(4)如果一条直线垂直于平面内的无数条直线,
那么这条直线垂直这个平面 ( )( )( )练习1:判断题
(5)如果一条直线垂直于平面内的任意两条直线,
那么这条直线垂直这个平面 ( )( )( )练习1:判断题
(6)如果一条直线垂直于平面内的两条相交直线,
那么这条直线垂直这个平面 ( )(7)过一点引已知平面的垂线有且仅有一条(8)过一点引已知直线的垂面有且仅有一条( )例1:如图所示,PA⊥平面ABC,BC⊥AB,
写出图中所有的直角三角形;解:图中共有四个直角三角形。Rt△ABC
Rt△PAB
Rt△PAC
Rt△PBC线面垂直的定义 线面垂直的判定定理线线垂直线面垂直关键:线不在多 相交则行线面垂直的定义3、课堂小结作业练习2: 如图: 在空间四边形ABCD中,
AB = AD, CB = CD,
求证: AC BD
证明:取 BD 中点E因为 AB=AD,E 是 BD 的中点
所以 AE BD 同理 EC BD 所以 BD 平面AEC 因为 AC 在平面AEC内所以 AC BDE
