比例 单元练习卷 人教版数学 六年级下册 (含答案)
文档属性
| 名称 | 比例 单元练习卷 人教版数学 六年级下册 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 373.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 11:07:35 | ||
图片预览



文档简介
比例 单元练习卷 人教版数学 六年级下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.a和b是两个相关联的量,且3a=5b,则a∶b=( ),a与b成( )比例关系。
2.在一个比例中,两个外项的积是12,其中一个内项是15,另一个内项是( )。
3.a与b的比是3∶4,b是c的,则( ),a比c少。
4.丽丽去北京动物园游玩,回家后把一张照片(如下图所示)在电脑上按一定的比例放大,放大后的照片长是14.4cm,放大后的宽是( )cm。
5.下图是从一幅地图上描下来的公路图,如果A站到货运总站的实际距离是120km,则这幅地图的比例尺是( ),A站到B站的实际距离是( )km。
6.如图,三角形BEF的面积比三角形ADF的面积少12平方厘米,三角形ABD的面积与三角形CDE的面积比是3∶5,求平行四边形ABCD的面积等于( )。
二、判断题
7.由两个比组成的式子叫做比例。( )
8.15∶5和1.2∶0.4能组成比例。( )
9.两个相关联的量不是正比例关系就是反比例关系。( )
10.在一个比例中,两个外项的积是4,一个内项是,另一个内项是9。( )
11.一个正方形按3∶1放大后,周长和面积都扩大到原来的3倍。( )
三、选择题
12.长方形的面积一定,它的长和宽( )。
A.不成比例 B.成正比例 C.成反比例
13.甲数的等于乙数的(甲数、乙数不为0),那么甲数与乙数的比是( )。
A. B.8∶15 C.15︰8
14.把一个边长2cm的正方形按4∶1放大后,面积是( )cm2。
A.8 B.32 C.64
15.一个圆柱侧面展开是正方形,这个圆柱底面直径与高的比是( )。
A.1∶ B.1∶1 C.
16.如图,灯塔在轮船( )。
A.北偏西50°方向75千米处
B.北偏东50°方向25千米处
C.北偏西50°方向25千米处
四、计算题
17.判断下面哪组中的两个比可以组成比例,把组成的比例写出来。
和 和 和 和
18.解比例。
五、解答题
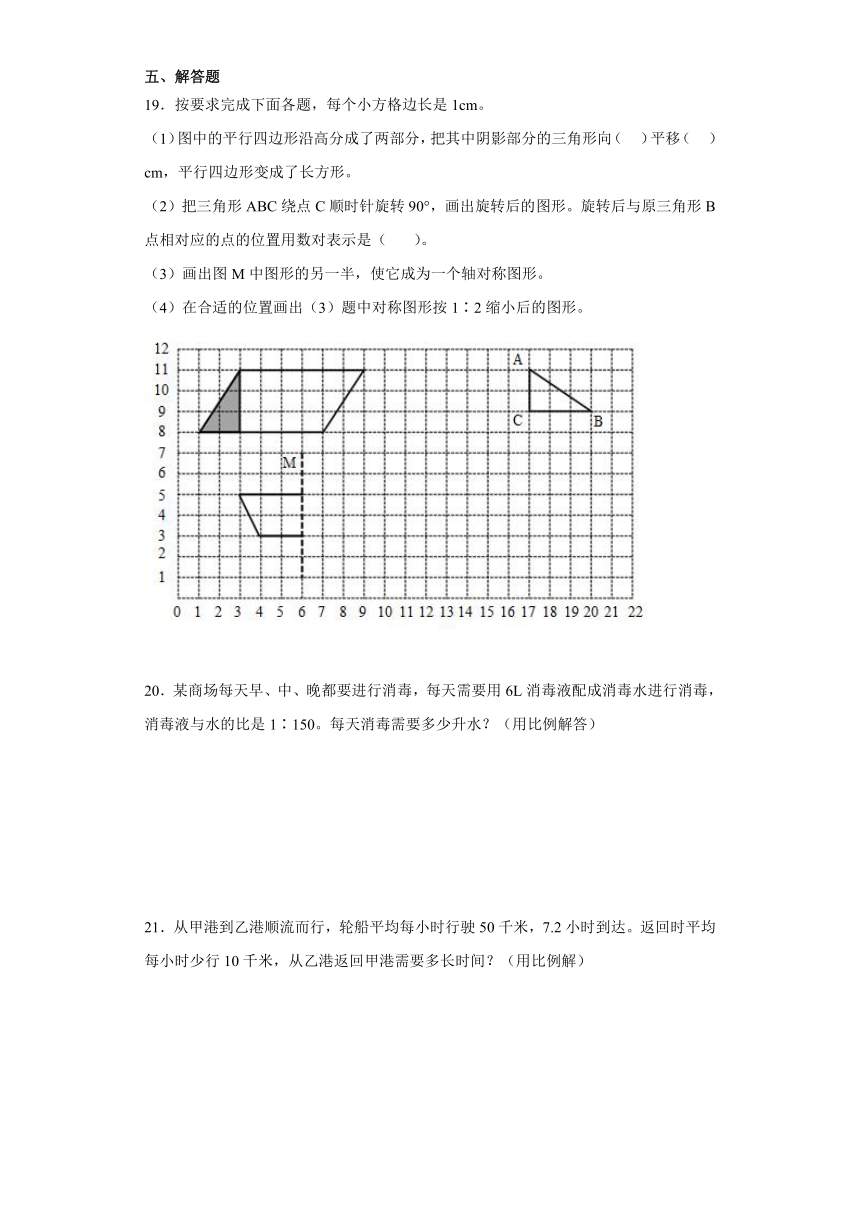
19.按要求完成下面各题,每个小方格边长是1cm。
(1)图中的平行四边形沿高分成了两部分,把其中阴影部分的三角形向( )平移( )cm,平行四边形变成了长方形。
(2)把三角形ABC绕点C顺时针旋转90°,画出旋转后的图形。旋转后与原三角形B点相对应的点的位置用数对表示是( )。
(3)画出图M中图形的另一半,使它成为一个轴对称图形。
(4)在合适的位置画出(3)题中对称图形按1∶2缩小后的图形。
20.某商场每天早、中、晚都要进行消毒,每天需要用6L消毒液配成消毒水进行消毒,消毒液与水的比是1∶150。每天消毒需要多少升水?(用比例解答)
21.从甲港到乙港顺流而行,轮船平均每小时行驶50千米,7.2小时到达。返回时平均每小时少行10千米,从乙港返回甲港需要多长时间?(用比例解)
22.在一幅比例尺为1∶20000000地图中,量得昆明到重庆之间的铁路长度是3.4cm,一辆高铁和一辆火车同时从两地相对开出,2.5小时相遇,高铁每小时行184千米,火车每小时行驶多少千米?(忽略车长)
23.一名考生步行前往考场,10分钟走了总路程的,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示,则他剩下的路程还要行驶多少分钟?
参考答案:
1. 5∶3 正
【分析】根据比例的基本性质,先将等积式改写成比例式,求出比值后再确定a和b是成正比例关系还是成反比例关系。
【详解】3a=5b,则a∶b=5∶3
a∶b=5∶3=
a∶b的比值一定,所以a和b成正比例关系。
【点睛】本题考查了比例的基本性质以及正比例关系,两个相关联的量,若其比值一定,这两个量成正比例关系;若其乘积一定,这两个量成反比例关系。
2.0.8
【分析】比例的基本性质:两个外项的积等于两个内项的积。
【详解】12÷15=0.8。
【点睛】本题考查比例的基本性质的应用。
3.3∶10;
【分析】b是c的,即b=c,又a与b的比是3∶4,将b用c进行等量代换,所以a∶c=3∶4,化简即可得a∶c的值;求a比c少几分之几,先求出(c-a),再除以c即可。
【详解】因为b=c,a∶b=3∶4,所以
a∶c=3∶4
c=4a
a∶c=3∶10
a为3份,c为10份
则a比c少几分之几列式为:
(10-3)÷10
=7÷10
=
【点睛】本题属于求多个数的连比和一个数比另一个数少几分之几的问题,要掌握等量代换的方法。
4.9.6
【分析】按照一定的比例进行图形放缩时,每条边是按照相同的比例放大的,这里长从6cm变成14.4cm,扩大了2.4倍,那么宽也要扩大2.4倍。
【详解】
(cm)
【点睛】本题考查的是图形的放缩,如果按照a∶1的比例进行放大,那么每条边都要扩大到原来的a倍,面积扩大到原来的a2倍。
5. 1∶6000000 360
【分析】从图中可知,A站到货运总站的图上距离是2cm,根据“比例尺=图上距离∶实际距离”,代入数据计算即可求出这幅地图的比例尺;从图中可知,A站到B站的图上距离是(2+4)cm,根据“实际距离=图上距离÷比例尺”,求出A站到B站的实际距离;注意单位的换算:1km=100000cm。
【详解】这幅地图的比例尺是:
2cm∶120km
=2cm∶(120×100000)cm
=2∶12000000
=(2÷2)∶(12000000÷2)
=1∶6000000
A站到B站的图上距离是:
2+4=6(cm)
A站到B站的实际距离是:
6÷=36000000(cm)
36000000cm=360km
【点睛】掌握图上距离、实际距离、比例尺之间的关系以及长度单位的换算是解题的关键。
6.72平方厘米
【分析】四边形ABCD是平行四边形,三角形ABD的面积等于三角形BCD的面积,都是平行四边形的一半;三角形CDE与三角形BCD的高相等,面积比等于底边长度比,那么BC∶CE=3∶5,可以求出EB∶BC=2∶3,而BC等于AD,那么EB∶AD=2∶3,再根据EB平行AD,得到三角形BEF与三角形ADF相似,然后利用相似求解。
【详解】三角形CDE与三角形BCD的高相等,面积比等于底边长度比,那么BC∶CE=3∶5;
可以求出EB∶BC=2∶3,而BC等于AD,那么EB∶AD=2∶3;
三角形BEF与三角形ADF的面积比是4∶9;
(平方厘米)
EF∶FD=2∶3
三角形BDF的面积:(平方厘米)
(平方厘米)
所以平行四边形ABCD的面积等于72平方厘米。
【点睛】本题用到了等高模型和相似模型,两个三角形高相等时,面积比等于对应的底边长度比。
7.×
【分析】根据比例的意义,表示两个比相等的式子叫做比例,来判断。
【详解】由分析可知,组成比例的两个比的比值是相等的,而不是任意两个比,故原题说法错误。
故答案为:×
【点睛】此题考查了比例的意义,掌握其中的关键点组成比例的两个比的比值是相等的。
8.√
【分析】分别算出15∶5和1.2∶0.4的比值,进行比较判断。
【详解】15∶5
=15÷5
=3
1.2∶0.4
=1.2÷0.4
=3
15∶5和1.2∶0.4能组成比例,原题说法正确。
故答案为:√
【点睛】本题考查成比例的意义,可以通过计算内项积与外项积进行比较,也可以分别算出比值进行比较判断。
9.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】两个相关联的量可能是正比例关系,也可能是反比例关系,也可能既不是正比例关系也不是反比例关系;例如:去超市购物,带的钱数和花的钱数是两个相关联的量,但既不是正比例关系也不是反比例关系。原题说法错误。
故答案为:×
【点睛】本题主要考查了正比例、反比例的意义和辨识。
10.√
【分析】根据比例的基本性质“在比例中,两外项之积等于两内项之积”,两外项之积是4,计算出两内项之积,是4就正确,否则错误。
【详解】解:两个外项的积是4;
×9=4,两内项之积是4,所以原题说法正确。
故答案为:√
【点睛】本题可根据比例的基本性质,比较两内项之积和两外项之积,得出答案。
11.×
【分析】图形放大或缩小后,对应边长的比相等,周长的比也相等,但面积比不相等,原图形按3∶1放大后,面积扩大到原来的32倍,据此解答。
【详解】一个正方形按3∶1放大后,现在周长∶原来的周长=3∶1=3,现在的面积∶原来的面积=32∶12=9∶1=9,所以周长扩大到原来的3倍,面积扩大到原来的9倍。
故答案为:×
【点睛】原图形按n∶1放大后,周长扩大到原来的n倍,面积扩大到原来的n2倍。
12.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答。
【详解】根据长方形的面积=长×宽,面积一定,即长和宽的乘积一定,符合反比例的定义,即长方形的长和宽成反比例。
故答案为:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
13.C
【分析】由题意可知:甲数×=乙数×,再逆运用比例的基本性质,即两内项之积等于两外项之积,即可求出二者的比。
【详解】由题意可知:甲数×=乙数×,根据比例的基本性质得:甲数∶乙数=∶=15∶8。
故答案为:C
【点睛】本题主要考查比例的基本性质。
14.C
【分析】把一个边长是2cm的正方形按4∶1放大后,也就是把这个正方形的边长扩大到原来的4倍,即边长乘4,我们知道正方形面积是边长×边长,即可求出放大后的正方形的面积。
【详解】(2×4)×(2×4)
=8×8
=64(cm2)
故答案为:C
【点睛】本题的解题关键是掌握图形放大与缩小后面积的计算方法。
15.A
【分析】根据一个圆柱体的侧面展开图是正方形,可得圆柱体的底面周长等于圆柱的高h;根据圆的周长等于圆的直径d乘,可得d=h;再根据比例的基本性质(两个外项的积等于两个内项的积),计算出底面直径与高的比。
【详解】设圆柱体的底面直径与高分别是d、h,则d=h。
因为d=h×1
所以d∶h=1∶
故答案为:A
【点睛】解决此题的关键是明确把圆柱沿高展开后得到的长方形(或正方形)的长等于圆柱的底面周长,长方形(或正方形)的宽等于圆柱的高。
16.C
【分析】指北针箭头指向上,根据实际方向与图上方向的关系“上北、下南、左西、右东”,按照图上方向确定实际方向。
【详解】图上灯塔在轮船的上偏左50°方向5个单位长度处,
由比例尺所示,一个单位长度是5千米,
5个单位长度是5×5=25(千米),
实际灯塔在轮船的北偏西50°方向25千米处。
故选:C。
【点睛】本题考查根据方向和距离确定物体的位置,熟练掌握实际方向与图上方向的关系,灵活运用图中比例尺解决问题。
17.不可以;可以;;
可以;;不可以
【分析】根据比例的基本性质可知,在比例中,两个外项的积等于两个内项的积。如果每一组中两个数的积等于另两个数的积,就存在比例关系。据此解答。
【详解】8×24=192,16×4=64,192≠64,所以和不能组成比例;
0.2×6.4=1.28,3.2×0.4=1.28,1.28=1.28,所以和能组成比例,组成的比例是;
,,2=2,所以和能组成比例,组成的比列是;
,,,所以和不能组成比例。
18.;;;
【分析】,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.2即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.4即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×8即可。
【详解】
解:
解:
解:
解:
19.(1)右;6
(2)见详解;(17,6)
(3)见详解
(4)见详解
【分析】第(1)问,以阴影三角形的顶点作为参考,向右平移6格可以拼成长方形;
第(2)问,绕点C顺时针旋转90°,AC边将变成水平的,BC边将变成竖直的;
第(3)问,找出左半部分各个顶点关于对称轴的对称点,然后依次连接顶点有半部分;
第(4)问,按1∶2缩小,需要将每条边的长度都变成原来的一半。;
【详解】如图所示:
(1)阴影部分的三角形向右平移6cm,平行四边形变成了长方形;
(2)旋转后与原三角形B点相对应的点的位置用数对表示是(17,6);
(3)、(4)如图所示。
【点睛】再进行图形放缩时,如果每条边都扩大到原来的a倍,那么面积将变成原来的a2倍。
20.900升
【分析】由题意可知:消毒液与水的比是1∶150,即消毒液与水的比值是一定的,则消毒液与水成正比例,据此即可列比例求解。
【详解】解:设每天消毒需要x升水,
6∶x=1∶150
x=150×6
x=900
答:每天消毒需要900升水。
【点睛】此题的解题关键是判定两种相关联的量是否成正、反比例,再采用相应的方法列比例,求解即可。
21.9小时
【分析】轮船从甲港到乙港,再返回,这两段的路程是相等的。路程(一定)=速度×时间,所以轮船的速度和时间成反比,据此将返回时间设为未知数,从而列比例解比例即可。
【详解】解:设从乙港返回甲港需要x小时。
(50-10)x=50×7.2
40x=360
x=360÷40
x=9
答:从乙港返回甲港需要9小时。
【点睛】本题考查了反比例的应用,能根据题意找出比例关系并列比例是解题的关键。
22.88千米
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出北京到洛阳的实际距离。再根据“相遇时间=路程÷速度之和”即可求出两车的速度和,再用速度和减高铁的速度,就得火车的速度。
【详解】实际距离:3.4÷=3.4×20000000=68000000(cm)=680km
680÷2.5-184
=272-184
=88(km)
答:火车每小时行驶88千米。
【点睛】此题主要考查图上距离、实际距离和比例尺之间的关系,以及相遇问题中的基本数量关系“相遇时间=路程÷速度之和”的灵活应用。
23.6分钟
【分析】从图中可以看出行驶10分钟之后的图像成正比例关键,这里出租车的速度一定,所以先算出剩下的路程=1-10分钟已经行走的路程,再算出租车的速度,用剩下的路程÷出租车的速度=剩下的路程需要的时间
【详解】÷2=
(1-)÷
=÷
=6(分钟)
答:他剩下的路程还要行驶6分钟。
【点睛】本题需要明确改乘出租车的速度一定,即路程和时间成正比例关系。
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.a和b是两个相关联的量,且3a=5b,则a∶b=( ),a与b成( )比例关系。
2.在一个比例中,两个外项的积是12,其中一个内项是15,另一个内项是( )。
3.a与b的比是3∶4,b是c的,则( ),a比c少。
4.丽丽去北京动物园游玩,回家后把一张照片(如下图所示)在电脑上按一定的比例放大,放大后的照片长是14.4cm,放大后的宽是( )cm。
5.下图是从一幅地图上描下来的公路图,如果A站到货运总站的实际距离是120km,则这幅地图的比例尺是( ),A站到B站的实际距离是( )km。
6.如图,三角形BEF的面积比三角形ADF的面积少12平方厘米,三角形ABD的面积与三角形CDE的面积比是3∶5,求平行四边形ABCD的面积等于( )。
二、判断题
7.由两个比组成的式子叫做比例。( )
8.15∶5和1.2∶0.4能组成比例。( )
9.两个相关联的量不是正比例关系就是反比例关系。( )
10.在一个比例中,两个外项的积是4,一个内项是,另一个内项是9。( )
11.一个正方形按3∶1放大后,周长和面积都扩大到原来的3倍。( )
三、选择题
12.长方形的面积一定,它的长和宽( )。
A.不成比例 B.成正比例 C.成反比例
13.甲数的等于乙数的(甲数、乙数不为0),那么甲数与乙数的比是( )。
A. B.8∶15 C.15︰8
14.把一个边长2cm的正方形按4∶1放大后,面积是( )cm2。
A.8 B.32 C.64
15.一个圆柱侧面展开是正方形,这个圆柱底面直径与高的比是( )。
A.1∶ B.1∶1 C.
16.如图,灯塔在轮船( )。
A.北偏西50°方向75千米处
B.北偏东50°方向25千米处
C.北偏西50°方向25千米处
四、计算题
17.判断下面哪组中的两个比可以组成比例,把组成的比例写出来。
和 和 和 和
18.解比例。
五、解答题
19.按要求完成下面各题,每个小方格边长是1cm。
(1)图中的平行四边形沿高分成了两部分,把其中阴影部分的三角形向( )平移( )cm,平行四边形变成了长方形。
(2)把三角形ABC绕点C顺时针旋转90°,画出旋转后的图形。旋转后与原三角形B点相对应的点的位置用数对表示是( )。
(3)画出图M中图形的另一半,使它成为一个轴对称图形。
(4)在合适的位置画出(3)题中对称图形按1∶2缩小后的图形。
20.某商场每天早、中、晚都要进行消毒,每天需要用6L消毒液配成消毒水进行消毒,消毒液与水的比是1∶150。每天消毒需要多少升水?(用比例解答)
21.从甲港到乙港顺流而行,轮船平均每小时行驶50千米,7.2小时到达。返回时平均每小时少行10千米,从乙港返回甲港需要多长时间?(用比例解)
22.在一幅比例尺为1∶20000000地图中,量得昆明到重庆之间的铁路长度是3.4cm,一辆高铁和一辆火车同时从两地相对开出,2.5小时相遇,高铁每小时行184千米,火车每小时行驶多少千米?(忽略车长)
23.一名考生步行前往考场,10分钟走了总路程的,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示,则他剩下的路程还要行驶多少分钟?
参考答案:
1. 5∶3 正
【分析】根据比例的基本性质,先将等积式改写成比例式,求出比值后再确定a和b是成正比例关系还是成反比例关系。
【详解】3a=5b,则a∶b=5∶3
a∶b=5∶3=
a∶b的比值一定,所以a和b成正比例关系。
【点睛】本题考查了比例的基本性质以及正比例关系,两个相关联的量,若其比值一定,这两个量成正比例关系;若其乘积一定,这两个量成反比例关系。
2.0.8
【分析】比例的基本性质:两个外项的积等于两个内项的积。
【详解】12÷15=0.8。
【点睛】本题考查比例的基本性质的应用。
3.3∶10;
【分析】b是c的,即b=c,又a与b的比是3∶4,将b用c进行等量代换,所以a∶c=3∶4,化简即可得a∶c的值;求a比c少几分之几,先求出(c-a),再除以c即可。
【详解】因为b=c,a∶b=3∶4,所以
a∶c=3∶4
c=4a
a∶c=3∶10
a为3份,c为10份
则a比c少几分之几列式为:
(10-3)÷10
=7÷10
=
【点睛】本题属于求多个数的连比和一个数比另一个数少几分之几的问题,要掌握等量代换的方法。
4.9.6
【分析】按照一定的比例进行图形放缩时,每条边是按照相同的比例放大的,这里长从6cm变成14.4cm,扩大了2.4倍,那么宽也要扩大2.4倍。
【详解】
(cm)
【点睛】本题考查的是图形的放缩,如果按照a∶1的比例进行放大,那么每条边都要扩大到原来的a倍,面积扩大到原来的a2倍。
5. 1∶6000000 360
【分析】从图中可知,A站到货运总站的图上距离是2cm,根据“比例尺=图上距离∶实际距离”,代入数据计算即可求出这幅地图的比例尺;从图中可知,A站到B站的图上距离是(2+4)cm,根据“实际距离=图上距离÷比例尺”,求出A站到B站的实际距离;注意单位的换算:1km=100000cm。
【详解】这幅地图的比例尺是:
2cm∶120km
=2cm∶(120×100000)cm
=2∶12000000
=(2÷2)∶(12000000÷2)
=1∶6000000
A站到B站的图上距离是:
2+4=6(cm)
A站到B站的实际距离是:
6÷=36000000(cm)
36000000cm=360km
【点睛】掌握图上距离、实际距离、比例尺之间的关系以及长度单位的换算是解题的关键。
6.72平方厘米
【分析】四边形ABCD是平行四边形,三角形ABD的面积等于三角形BCD的面积,都是平行四边形的一半;三角形CDE与三角形BCD的高相等,面积比等于底边长度比,那么BC∶CE=3∶5,可以求出EB∶BC=2∶3,而BC等于AD,那么EB∶AD=2∶3,再根据EB平行AD,得到三角形BEF与三角形ADF相似,然后利用相似求解。
【详解】三角形CDE与三角形BCD的高相等,面积比等于底边长度比,那么BC∶CE=3∶5;
可以求出EB∶BC=2∶3,而BC等于AD,那么EB∶AD=2∶3;
三角形BEF与三角形ADF的面积比是4∶9;
(平方厘米)
EF∶FD=2∶3
三角形BDF的面积:(平方厘米)
(平方厘米)
所以平行四边形ABCD的面积等于72平方厘米。
【点睛】本题用到了等高模型和相似模型,两个三角形高相等时,面积比等于对应的底边长度比。
7.×
【分析】根据比例的意义,表示两个比相等的式子叫做比例,来判断。
【详解】由分析可知,组成比例的两个比的比值是相等的,而不是任意两个比,故原题说法错误。
故答案为:×
【点睛】此题考查了比例的意义,掌握其中的关键点组成比例的两个比的比值是相等的。
8.√
【分析】分别算出15∶5和1.2∶0.4的比值,进行比较判断。
【详解】15∶5
=15÷5
=3
1.2∶0.4
=1.2÷0.4
=3
15∶5和1.2∶0.4能组成比例,原题说法正确。
故答案为:√
【点睛】本题考查成比例的意义,可以通过计算内项积与外项积进行比较,也可以分别算出比值进行比较判断。
9.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】两个相关联的量可能是正比例关系,也可能是反比例关系,也可能既不是正比例关系也不是反比例关系;例如:去超市购物,带的钱数和花的钱数是两个相关联的量,但既不是正比例关系也不是反比例关系。原题说法错误。
故答案为:×
【点睛】本题主要考查了正比例、反比例的意义和辨识。
10.√
【分析】根据比例的基本性质“在比例中,两外项之积等于两内项之积”,两外项之积是4,计算出两内项之积,是4就正确,否则错误。
【详解】解:两个外项的积是4;
×9=4,两内项之积是4,所以原题说法正确。
故答案为:√
【点睛】本题可根据比例的基本性质,比较两内项之积和两外项之积,得出答案。
11.×
【分析】图形放大或缩小后,对应边长的比相等,周长的比也相等,但面积比不相等,原图形按3∶1放大后,面积扩大到原来的32倍,据此解答。
【详解】一个正方形按3∶1放大后,现在周长∶原来的周长=3∶1=3,现在的面积∶原来的面积=32∶12=9∶1=9,所以周长扩大到原来的3倍,面积扩大到原来的9倍。
故答案为:×
【点睛】原图形按n∶1放大后,周长扩大到原来的n倍,面积扩大到原来的n2倍。
12.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答。
【详解】根据长方形的面积=长×宽,面积一定,即长和宽的乘积一定,符合反比例的定义,即长方形的长和宽成反比例。
故答案为:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
13.C
【分析】由题意可知:甲数×=乙数×,再逆运用比例的基本性质,即两内项之积等于两外项之积,即可求出二者的比。
【详解】由题意可知:甲数×=乙数×,根据比例的基本性质得:甲数∶乙数=∶=15∶8。
故答案为:C
【点睛】本题主要考查比例的基本性质。
14.C
【分析】把一个边长是2cm的正方形按4∶1放大后,也就是把这个正方形的边长扩大到原来的4倍,即边长乘4,我们知道正方形面积是边长×边长,即可求出放大后的正方形的面积。
【详解】(2×4)×(2×4)
=8×8
=64(cm2)
故答案为:C
【点睛】本题的解题关键是掌握图形放大与缩小后面积的计算方法。
15.A
【分析】根据一个圆柱体的侧面展开图是正方形,可得圆柱体的底面周长等于圆柱的高h;根据圆的周长等于圆的直径d乘,可得d=h;再根据比例的基本性质(两个外项的积等于两个内项的积),计算出底面直径与高的比。
【详解】设圆柱体的底面直径与高分别是d、h,则d=h。
因为d=h×1
所以d∶h=1∶
故答案为:A
【点睛】解决此题的关键是明确把圆柱沿高展开后得到的长方形(或正方形)的长等于圆柱的底面周长,长方形(或正方形)的宽等于圆柱的高。
16.C
【分析】指北针箭头指向上,根据实际方向与图上方向的关系“上北、下南、左西、右东”,按照图上方向确定实际方向。
【详解】图上灯塔在轮船的上偏左50°方向5个单位长度处,
由比例尺所示,一个单位长度是5千米,
5个单位长度是5×5=25(千米),
实际灯塔在轮船的北偏西50°方向25千米处。
故选:C。
【点睛】本题考查根据方向和距离确定物体的位置,熟练掌握实际方向与图上方向的关系,灵活运用图中比例尺解决问题。
17.不可以;可以;;
可以;;不可以
【分析】根据比例的基本性质可知,在比例中,两个外项的积等于两个内项的积。如果每一组中两个数的积等于另两个数的积,就存在比例关系。据此解答。
【详解】8×24=192,16×4=64,192≠64,所以和不能组成比例;
0.2×6.4=1.28,3.2×0.4=1.28,1.28=1.28,所以和能组成比例,组成的比例是;
,,2=2,所以和能组成比例,组成的比列是;
,,,所以和不能组成比例。
18.;;;
【分析】,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.2即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.4即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×8即可。
【详解】
解:
解:
解:
解:
19.(1)右;6
(2)见详解;(17,6)
(3)见详解
(4)见详解
【分析】第(1)问,以阴影三角形的顶点作为参考,向右平移6格可以拼成长方形;
第(2)问,绕点C顺时针旋转90°,AC边将变成水平的,BC边将变成竖直的;
第(3)问,找出左半部分各个顶点关于对称轴的对称点,然后依次连接顶点有半部分;
第(4)问,按1∶2缩小,需要将每条边的长度都变成原来的一半。;
【详解】如图所示:
(1)阴影部分的三角形向右平移6cm,平行四边形变成了长方形;
(2)旋转后与原三角形B点相对应的点的位置用数对表示是(17,6);
(3)、(4)如图所示。
【点睛】再进行图形放缩时,如果每条边都扩大到原来的a倍,那么面积将变成原来的a2倍。
20.900升
【分析】由题意可知:消毒液与水的比是1∶150,即消毒液与水的比值是一定的,则消毒液与水成正比例,据此即可列比例求解。
【详解】解:设每天消毒需要x升水,
6∶x=1∶150
x=150×6
x=900
答:每天消毒需要900升水。
【点睛】此题的解题关键是判定两种相关联的量是否成正、反比例,再采用相应的方法列比例,求解即可。
21.9小时
【分析】轮船从甲港到乙港,再返回,这两段的路程是相等的。路程(一定)=速度×时间,所以轮船的速度和时间成反比,据此将返回时间设为未知数,从而列比例解比例即可。
【详解】解:设从乙港返回甲港需要x小时。
(50-10)x=50×7.2
40x=360
x=360÷40
x=9
答:从乙港返回甲港需要9小时。
【点睛】本题考查了反比例的应用,能根据题意找出比例关系并列比例是解题的关键。
22.88千米
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出北京到洛阳的实际距离。再根据“相遇时间=路程÷速度之和”即可求出两车的速度和,再用速度和减高铁的速度,就得火车的速度。
【详解】实际距离:3.4÷=3.4×20000000=68000000(cm)=680km
680÷2.5-184
=272-184
=88(km)
答:火车每小时行驶88千米。
【点睛】此题主要考查图上距离、实际距离和比例尺之间的关系,以及相遇问题中的基本数量关系“相遇时间=路程÷速度之和”的灵活应用。
23.6分钟
【分析】从图中可以看出行驶10分钟之后的图像成正比例关键,这里出租车的速度一定,所以先算出剩下的路程=1-10分钟已经行走的路程,再算出租车的速度,用剩下的路程÷出租车的速度=剩下的路程需要的时间
【详解】÷2=
(1-)÷
=÷
=6(分钟)
答:他剩下的路程还要行驶6分钟。
【点睛】本题需要明确改乘出租车的速度一定,即路程和时间成正比例关系。
