人教版五年级上册数学巧借梯形和三角形面积公式探索规律课件(25张PPT)
文档属性
| 名称 | 人教版五年级上册数学巧借梯形和三角形面积公式探索规律课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 305.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 11:08:39 | ||
图片预览






文档简介
(共25张PPT)
巧借梯形和三角形面积公式探索规律
一点一滴的努力,
一尺一寸的收获。
巧借梯形和三角形面积公式
梯形的面积=(上底+下底)×高÷2
当梯形的上底为0时,它就变成了一个三角形。
三角形的面积=底×高÷2
圆木根数=(顶层根数+底层根数)×层数÷2
横截面是梯形形状的一堆有规律摆放的物体(只计横截面)的个数可以用如下的公式表示:
总个数=(顶层数+底层数)×层数÷2
(或 总个数=底层数×层数÷2)(0也算一层)
田忌赛马
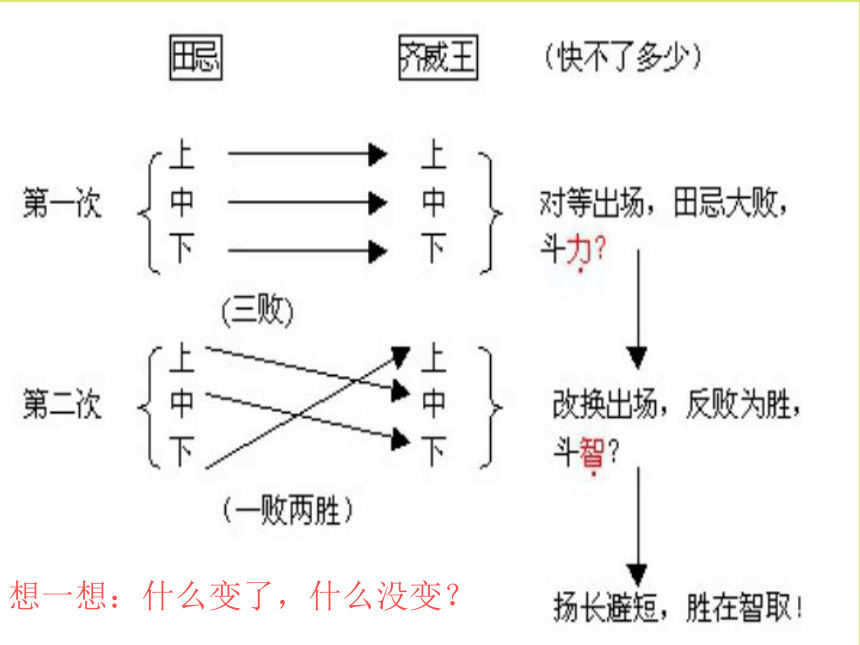
想一想:什么变了,什么没变?
田忌的马还是那三匹马,只是改变了马匹出场的顺序,便反败为胜。
我们的整数和小数四则混合运算中同样蕴含着这样的智慧。我们可以运用计算法则和运算定律适当改变一个算式的运算顺序或结构,就可以使计算简便。
用简便算法计算
11 × 9.9 - 3.6 - 6.3
98 × 99 ÷ 2
孙膑的智慧
四两拨千斤
例.1(小组合作,说一说,摆一摆,算一算)
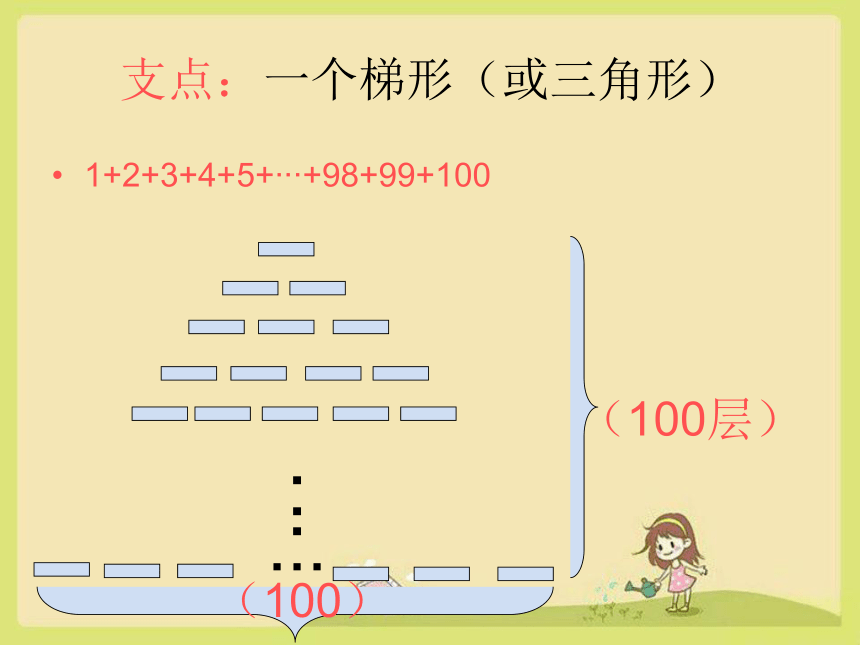
1+2+3+4+5+ +98+99+100
先找到撬动千斤大石的杠杆和支点
杠杆:总个数=(顶层数+底层数)×层数÷2
1+2+3+4+5+ +98+99+100
支点:一个梯形(或三角形)
(100层)
(100)
总数=(顶层数+底层数)×层数÷2
(1+100)×100÷2
=101×100÷2
=10100÷2
=5050
从1开始的n个连续自然数的和可以用如下的式子表示:
(1+n)×n÷2
100以内所有奇数的和是多少?
1+3+5+ +95+97+99
=(1+99)×50÷2
=100×50÷2
=5000÷2
=2500
从2到100的所有偶数的和是多少?
2+4+6+ +96+98+100
=(2+100)×50÷2
=102×50÷2
=5100÷2
=2550
从0到100的所有偶数的和是多?
0+2+4+6+ +96+98+100
=(0+100)×51÷2
=100×51÷2
=5100÷2
=2550
例2. 在同一平面内,任意三点都不在同一条
直线上的99个点,能确定多少条直线?
经过一点可以画无数条直线,但不能确定一条直线。
两点确定一条直线
三点确定三条直线
0条
0+1=1(条)
0+1+2=3(条)
那四点呢?五点呢?
四个点确定6条直线
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
五个点确定10条直线
●
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
5个点 0+1+2+3+4=10(条)
讨论:你发现了什么?
每次增加的直线条数比对应的点数少1
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
5个点 0+1+2+3+4=10(条)
6个点 0+1+2+3+4+5=15(条)
100个点 0+1+2+3+4+5+ +98+99=?(条)
0+1+2+3+4+5+ +98+99 (转化成图形)
(100层)
(99条)
0
1
2
3
4
5
6
100
0+1+2+3+4+5+ +98+99=?(条)
直线总数=底层数×层数÷2
=99×100÷2
=9900÷2
=4950(条)
在同一平面内,任意三点都不在同一条直线上的n个点,能确定多少条直线?
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
5个点 0+1+2+3+4=10(条)
6个点 0+1+2+3+4+5=15(条)
n个点 0+1+2+3+4+5+ +(n-1)=?(条)
0+1+2+3+4+5+ +(n-2)+(n-1)
(n层)
(n-1条)
0
1
2
3
4
5
6
n
n表示点数
在同一平面内,任意三点都不在同一条直线上的n个点,能确定多少条直线的公式
直线总数=底层数×层数÷2
C总数=(n-1)×n÷2
在同一平面内,任意三点都不在同一条直线上的99个点,能确定多少条直线
0+1+2+3+4+5+ +97+98=?(条)
(99层)
(98条)
0
1
2
3
4
5
6
99
在同一平面内,任意三点都不在同一条直线上的99个点,能确定多少条直线?
直线总数=底层数×层数÷2
C总数=(n-1)×n÷2
=(99-1)×99÷2
=98×99÷2
=98×(100-1)÷2
=(9800-98)÷2
=9702÷2
=4851(条)
在同一平面内,任意三点都不在同一条直线上的101个点,能确定多少条直线?
直线总数=底层数×层数÷2
C总数=(n-1)×n÷2
=(101-1)×101÷2
=100×101÷2
=10100÷2
=5050(条)
抢答:
恭喜你答对了!
课堂小结
1、这节课我们学习了哪些知识?
2、你有什么收获?
巧借梯形和三角形面积公式探索规律
一点一滴的努力,
一尺一寸的收获。
巧借梯形和三角形面积公式
梯形的面积=(上底+下底)×高÷2
当梯形的上底为0时,它就变成了一个三角形。
三角形的面积=底×高÷2
圆木根数=(顶层根数+底层根数)×层数÷2
横截面是梯形形状的一堆有规律摆放的物体(只计横截面)的个数可以用如下的公式表示:
总个数=(顶层数+底层数)×层数÷2
(或 总个数=底层数×层数÷2)(0也算一层)
田忌赛马
想一想:什么变了,什么没变?
田忌的马还是那三匹马,只是改变了马匹出场的顺序,便反败为胜。
我们的整数和小数四则混合运算中同样蕴含着这样的智慧。我们可以运用计算法则和运算定律适当改变一个算式的运算顺序或结构,就可以使计算简便。
用简便算法计算
11 × 9.9 - 3.6 - 6.3
98 × 99 ÷ 2
孙膑的智慧
四两拨千斤
例.1(小组合作,说一说,摆一摆,算一算)
1+2+3+4+5+ +98+99+100
先找到撬动千斤大石的杠杆和支点
杠杆:总个数=(顶层数+底层数)×层数÷2
1+2+3+4+5+ +98+99+100
支点:一个梯形(或三角形)
(100层)
(100)
总数=(顶层数+底层数)×层数÷2
(1+100)×100÷2
=101×100÷2
=10100÷2
=5050
从1开始的n个连续自然数的和可以用如下的式子表示:
(1+n)×n÷2
100以内所有奇数的和是多少?
1+3+5+ +95+97+99
=(1+99)×50÷2
=100×50÷2
=5000÷2
=2500
从2到100的所有偶数的和是多少?
2+4+6+ +96+98+100
=(2+100)×50÷2
=102×50÷2
=5100÷2
=2550
从0到100的所有偶数的和是多?
0+2+4+6+ +96+98+100
=(0+100)×51÷2
=100×51÷2
=5100÷2
=2550
例2. 在同一平面内,任意三点都不在同一条
直线上的99个点,能确定多少条直线?
经过一点可以画无数条直线,但不能确定一条直线。
两点确定一条直线
三点确定三条直线
0条
0+1=1(条)
0+1+2=3(条)
那四点呢?五点呢?
四个点确定6条直线
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
五个点确定10条直线
●
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
5个点 0+1+2+3+4=10(条)
讨论:你发现了什么?
每次增加的直线条数比对应的点数少1
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
5个点 0+1+2+3+4=10(条)
6个点 0+1+2+3+4+5=15(条)
100个点 0+1+2+3+4+5+ +98+99=?(条)
0+1+2+3+4+5+ +98+99 (转化成图形)
(100层)
(99条)
0
1
2
3
4
5
6
100
0+1+2+3+4+5+ +98+99=?(条)
直线总数=底层数×层数÷2
=99×100÷2
=9900÷2
=4950(条)
在同一平面内,任意三点都不在同一条直线上的n个点,能确定多少条直线?
1个点 0条
2个点 0+1=1(条)
3个点 0+1+2=3(条)
4个点 0+1+2+3=6(条)
5个点 0+1+2+3+4=10(条)
6个点 0+1+2+3+4+5=15(条)
n个点 0+1+2+3+4+5+ +(n-1)=?(条)
0+1+2+3+4+5+ +(n-2)+(n-1)
(n层)
(n-1条)
0
1
2
3
4
5
6
n
n表示点数
在同一平面内,任意三点都不在同一条直线上的n个点,能确定多少条直线的公式
直线总数=底层数×层数÷2
C总数=(n-1)×n÷2
在同一平面内,任意三点都不在同一条直线上的99个点,能确定多少条直线
0+1+2+3+4+5+ +97+98=?(条)
(99层)
(98条)
0
1
2
3
4
5
6
99
在同一平面内,任意三点都不在同一条直线上的99个点,能确定多少条直线?
直线总数=底层数×层数÷2
C总数=(n-1)×n÷2
=(99-1)×99÷2
=98×99÷2
=98×(100-1)÷2
=(9800-98)÷2
=9702÷2
=4851(条)
在同一平面内,任意三点都不在同一条直线上的101个点,能确定多少条直线?
直线总数=底层数×层数÷2
C总数=(n-1)×n÷2
=(101-1)×101÷2
=100×101÷2
=10100÷2
=5050(条)
抢答:
恭喜你答对了!
课堂小结
1、这节课我们学习了哪些知识?
2、你有什么收获?
