人教版六年级下册数学第四单元单元专项训练——应用题(含答案)
文档属性
| 名称 | 人教版六年级下册数学第四单元单元专项训练——应用题(含答案) | 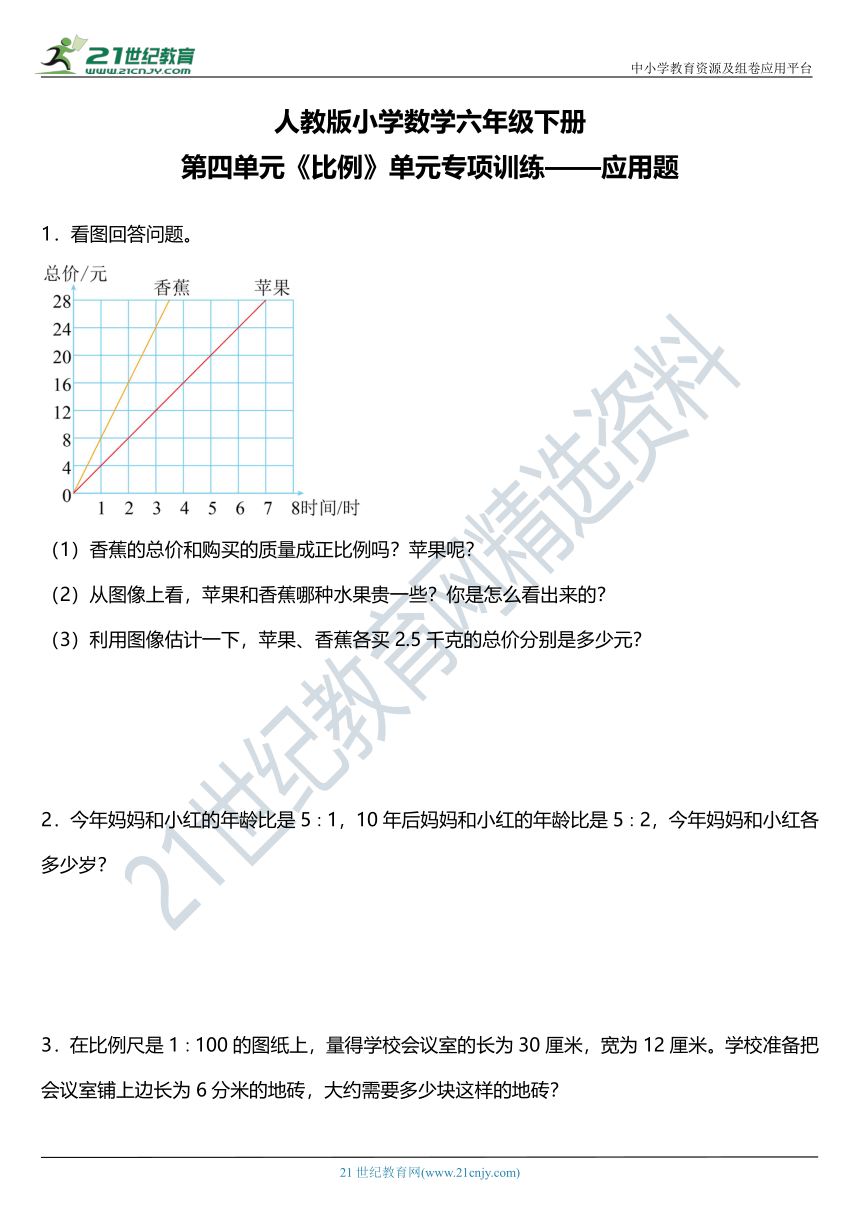 | |
| 格式 | doc | ||
| 文件大小 | 840.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 08:15:25 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
人教版小学数学六年级下册
第四单元《比例》单元专项训练——应用题
1.看图回答问题。
(1)香蕉的总价和购买的质量成正比例吗?苹果呢?
(2)从图像上看,苹果和香蕉哪种水果贵一些?你是怎么看出来的?
(3)利用图像估计一下,苹果、香蕉各买2.5千克的总价分别是多少元?
2.今年妈妈和小红的年龄比是5∶1,10年后妈妈和小红的年龄比是5∶2,今年妈妈和小红各多少岁?
3.在比例尺是1∶100的图纸上,量得学校会议室的长为30厘米,宽为12厘米。学校准备把会议室铺上边长为6分米的地砖,大约需要多少块这样的地砖?
4.王叔叔用180厘米长的铁丝围成一个长和宽的比是3∶2的长方形,然后用1∶9的比例尺,把这个长方形画到图纸上,这个长方形在图纸上的面积是多少平方厘米?
5.国家游泳中心“水立方”改造成“冰立方”,成为冬奥会历史上体量最大的冰壶场馆。冰壶场地是由长50米、宽25米、深约3米的泳池改造而成的,如果将这个泳池的平面图画在比例尺是1∶200的图纸上,长和宽各应画多少厘米?
6.按3∶1画出平行四边形A放大后得到的平行四边形B,再画出把平行四边形B按1∶2缩小后得到的平行四边形C。
(1)哪些图形是由平行四边形A放大后得到的?哪些图形是由平行四边形B缩小后得到的?
(2)观察平行四边形A和B,它们的面积有什么变化?面积与边长是按相同的比变化的吗?
7.一瓶消毒液的标签上写着:“将原液和清水按1∶400配置使用”,倒出原液4克,应加多少克清水?(用比例解答)
8.在比例尺为1∶5000000的地图上量的甲、乙两地的距离是12.6厘米,客车和货车分别从两地同时出发相向而行,5小时后两车相遇。已知客车的速度是每小时70千米,货车的速度是每小时多少千米?
9.在一幅地图上,用6厘米的距离表示实际距离1200千米。在这幅地图上量得A、B两地的距离是4.5厘米,A、B两地的实际距离是多少千米?一条560千米的高速公路,在这幅地图上是多少厘米?
10.一批桃子,如果每箱装30个,那么可以装12箱。如果每个箱子多装10个桃子,那么可以装多少箱?(用比例知识解答)
11.如图是比例尺为1∶100的圆形水池平面图,工人要在圆形水池的周围修一条宽是1米的环形小路,请画出这条小路,并计算环形小路的面积。
12.下面是某市人民路路段的部分平面图。
(1)超市在公园( )面,距离公园( )米处。
(2)小艺家在公园( )偏( )( )°方向,距离公园( )米处。
(3)公园东面1500米处,有一条与人民路垂直且长度差不多的共和路,在图中画线段表示共和路。
(4)小艺乘出租车沿图中所示的路线从家到超市,按以下收费标准她需要支付多少车费?
某市出租车收费标准
里程 收费
2km及以下 9元
2km以上每增加1km(不足1km按1km计算) 1.9元
13.在一幅比例尺是1∶9000000的地图上,量得京沪高速公路的全长是14厘米,两辆汽车分别同时从北京和上海出发相向而行,6小时后两车在距两地中点60千米处相遇。已知慢车的速度是95千米/时,快车的速度是多少?
14.在一幅比例尺是1∶4000000的地图上,量得亮亮家到某景点的距离是10.5厘米。如果他们7:00自驾从家出发,以80千米/时的平均速度行驶,12:00能赶到景点吗?
15.下图是洛阳地铁1号线,它覆盖洛北地区东西方向主要客流,连接涧西、西工、老城、瀍河4个城市区。下图比例尺是1∶300000,地铁1号线的图上距离约为8.4厘米。
(1)请计算出地铁1号线实际距离约为多少千米?
(2)计划开建的洛阳地铁4号线全长17.4公里,地铁4号线在这张地图上约多少厘米?
16.洛阳地铁2号线整条线路全长约18.3千米,地铁列车10分钟大约可运行6.1千米,照这样计算,跑完2号线全程大约需多少分钟?(用比例解)
17.一辆客车和一辆货车同时从A、B两地相对开出,它们的速度之比是6∶5,相遇时客车行驶了96千米,货车行驶了多少千米?(用比例解答)
18.在比例尺是1∶500000的地图上,量得甲、乙两城之间的距离是6厘米。一辆汽车从甲城到乙城,每小时行60千米,需要几小时到达?
19.在一幅比例尺是1∶10000000的地图上,量得榆林到延安的图上距离是2.7厘米,榆林到延安的实际距离是多少?
20.琪琪身高1.5米,阳光下她的影长为2米,此时测得一个水塔在同一地面的影长为60米,水塔的高度是几米?
21.在比例尺是1∶5000000的地图上,量得甲地到乙地的距离是3.6厘米。一辆汽车上午8时以每小时60千米的速度从甲地出发,这辆汽车到达乙地是几时?
22.为庆祝六一儿童节,实验小学举行团体操表演,如果每行站25人,那么正好站24行;如果每行站30人,那么可以站多少行?(用比例知识解答)
23.甲、乙两地相距520千米。一辆汽车从甲地出发开往乙地,前3小时行驶了240千米。照这样的速度,到达乙地一共需要多少小时?(用比例解)
24.某工程队铺一条管道,前6天铺了240米,照这样计算,还要8天才能把管道铺完,这条管道一共长多少米?(用比例知识解答)
25.学校要挖一个长方体泳池,在比例尺是1∶200的设计图上,水池的长为5厘米,宽为3厘米,深为1厘米。
(1)按图施工,这个水池的长、宽、深各应挖多少米?
(2)沿泳池内壁距池口0.6米处用红漆画一条警戒水位线,警戒水位线全长多少米?
(3)池底有根排水管,内直径2分米,放水时,水流速度平均每秒4.5米。放完池中警戒水位以下的水大约需要多少分钟?(结果保留整数)
参考答案:
1.(1)香蕉的总价和购买的质量成正比例;苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;由图像可知,1千克香蕉8元,1千克苹果4元,所以香蕉贵一些。
(3)苹果总价10元;香蕉总价20元。
【分析】(1)总价÷数量=单价,选择几组数据计算香蕉和苹果的单价 ,如果单价一定,则总价和购买的质量成正比例;
(2)有2种方法:①观察同样的质量,对比总价,哪种的总价更高,则哪种水果更贵;②同样的总价,对比质量,哪种的质量更少,则哪种水果更贵;(合理即可,答案不唯一)
(3)观察图像可知,1千克苹果4元,1千克香蕉8元,总价=单价×数量,代入数据计算即可。
【详解】(1)香蕉:(元)
(元)
(元)
香蕉的单价为每千克8元(一定),所以香蕉的总价和购买的质量成正比例。
苹果:(元)
(元)
(元)
苹果的单价为每千克4元(一定),所以苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;观察图像可知,1千克苹果4元,1千克香蕉8元,所以香蕉贵一些。(合理即可,答案不唯一)
(3)苹果:(元)
香蕉:(元)
答:2.5千克苹果的总价为10元,2.5千克香蕉的总价为20元。
2.30岁;6岁
【分析】
由题意可知,设小红今年的年龄是x岁,则妈妈今年的年龄是5x岁,10年后小红的年龄为(x+10)岁,妈妈的年龄为(5x+10)岁,再结合10年后妈妈和小红的年龄比是5∶2,据此列比例解答即可。
【详解】
解:设小红今年的年龄是x岁,则妈妈今年的年龄是5x岁。
(5x+10)∶(x+10)=5∶2
5×(x+10)=2×(5x+10)
5x+50=10x+20
5x+50-5x=10x+20-5x
5x+20=50
5x+20-20=50-20
5x=30
x=30÷5
x=6
5×6=30(岁)
答:今年妈妈30岁,小红6岁。
3.1000块
【分析】
根据实际距离=图上距离÷比例尺,代入数据分别求出该会议室的长和宽的实际厘米数,由低级单位厘米转换成高级单位分米,除以进率10,据此将长和宽的实际厘米数转换成以分米为单位;
根据长方形面积=长×宽,代入数据求出会议室的面积,再根据正方形面积=边长×边长,代入数据求出地砖的面积,最后用会议室的面积除以地砖的面积即可求出需要几块这样的地砖。
【详解】
由分析可得:
30×100=3000(厘米)
3000厘米=3000÷10=300(分米)
12×100=1200(厘米)
1200厘米=1200÷10=120(分米)
300×120÷(6×6)
=300×120÷36
=36000÷36
=1000(块)
答:大约需要1000块这样的地砖。
4.24平方厘米
【分析】
长方形的周长等于两条长和两条宽的和,用180除以2,可得该长方形一条长和一条宽的和,因为长和宽的比是3∶2,将一条长和一条宽的和看作单位“1”,根据分数乘法的意义,求一个数的几分之几是多少用乘法,即分别用单位“1”乘和可求出长方形实际的长和宽各是多少厘米;
再根据图上距离=实际距离×比例尺,用求出的长和宽分别乘比例尺,即可求出长方形在图纸上的长和宽分别是多少厘米;
最后根据长方形面积=长×宽,代入数据求出长方形图上的面积即可。
【详解】
由分析可得:
180÷2=90(厘米)
长:(厘米)
宽:(厘米)
(厘米)
(厘米)
6×4=24(平方厘米)
答:这个长方形在图纸上的面积是24平方厘米。
5.25厘米;12.5厘米
【分析】将这个泳池的平面图画在比例尺是1∶200的图纸上,也就是将实际长度缩短到原来的,用实际长度乘,就是图纸上的长度。据此解答。
【详解】
50米=5000厘米
25米=2500厘米
5000×=25(厘米)
2500×=12.5(厘米)
答:长应画25厘米,宽应画12.5厘米。
6.
见详解
【分析】按3∶1放大,就是放大到原图面积的3倍,将平行四边形A的底放大到6,高放大到6,就是放大的图形B;
按1∶2缩小就是缩小到原来的,将图形B的底缩小到 3、高缩小到3就得到图形C。
【详解】
(1)图形B和C是图形A放大后得到的;图形A和图形C是图形B缩小后得到的。
(2)图形A:2×2=4;图形B:6×6=36;36÷4=9
图形B面积是图形A面积的9倍,面积与边长不是按相同的比变化的。
7.1600克
【分析】根据题意可知,原液的质量∶清水的质量=1∶400,据此列出比例方程,并求解。
【详解】解:设应加克清水。
4∶=1∶400
×1=4×400
=1600
答:应加1600克清水。
8.56千米
【分析】根据实际距离=图上距离÷比例尺,据此求出甲、乙两地的实际距离;然后设货车的速度是每小时x千米,再根据相遇问题中的等量关系:速度和×相遇时间=路程和,据此列方程解答即可。
【详解】解:设货车的速度是每小时x千米。
12.6÷=12.6×5000000=63000000(厘米)
63000000厘米=630千米
(70+x)×5=630
(70+x)×5÷5=630÷5
70+x=126
70+x-70=126-70
x=56
答:货车的速度是每小时56千米。
9.900千米;2.8厘米
【分析】根据比例尺=图上距离∶实际距离,据此求出这幅地图的比例尺,再根据实际距离=图上距离÷比例尺,据此计算可求出A、B两地的实际距离;根据图上距离=实际距离×比例尺,据此可求出一条560千米的高速公路,在这幅地图上是多少厘米。
【详解】6厘米∶1200千米
=6厘米∶120000000厘米
=6∶120000000
=(6÷6)∶(120000000÷6)
=1∶20000000
4.5÷=4.5×20000000=90000000(厘米)
90000000厘米=900千米
560千米=56000000厘米
56000000×=2.8(厘米)
答:A、B两地的实际距离是900千米,一条560千米的高速公路,在这幅地图上是2.8厘米。
10.9箱
【分析】由题意可知,设可以装x箱,这批桃子的数量一定,则每箱装的个数与箱数成反比例关系,据此列比例解答即可。
【详解】解:设可以装x箱。
30×12=(30+10)x
40x=360
40x÷40=360÷40
x=9
答:可以装9箱。
11.画图见详解;9.42平方米
【分析】画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
根据图上距离=实际距离×比例尺,求出小路图上宽,测量出水池图上半径,小路宽+水池半径=大圆半径,据此根据画圆的方法画出小路。
根据实际距离=图上距离÷比例尺,确定大圆和小圆半径,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】测量可知,一格长1厘米,即圆形水池半径图上1厘米。
1米=100厘米
100×=1(厘米)
1+1=2(厘米)
1÷=1×100=100(厘米)=1(米)
2÷=2×100=200(厘米)=2(米)
3.14×(22-12)
=3.14×(4-1)
=3.14×3
=9.42(平方米)
答:环形小路的面积是9.42平方米。
12.(1)东;2700
(2)北;西;30;1800
(3)见详解
(4)14.7元
【分析】(1)经过测量得到,公园到超市的图上距离是2.7厘米,根据“实际距离=图上距离÷比例尺”可以计算出实际距离,图上的方向是上北下南,左西右东,据此得到超市在公园东面;
(2)应用方位角表示位置,要确定方向和距离。首先根据公园到小艺家的图上距离是1.8厘米,计算出实际距离,再用“方向+偏移角度”表示即可;
(3)计算出实际距离是1500米的图上距离,也就确定了共和路与人民路的交点,再在交点处画出垂直于人民路的共和路(长度与人民路差不多)即可;
(4)根据(1)、(2)计算出从家到超市的实际距离,对照收费标准,看看计费里程约是多少,按照收费标准计算车费。
【详解】(1)(厘米)=2700(米)
超市在公园东面,距离公园2700米处。
(2)(厘米)=1800(米)
小艺家在公园北偏西30°(西偏北60°)方向,距离公园1800米处。
(3)(米)=1.5(厘米)
(4)(米)=4.5(千米)
(千米)
(元)
答:她需要支付14.7元车费。
13.115千米/时
【分析】两车在距两地中点60千米处相遇,说明相遇时,快车比慢车多行驶(60×2)千米,设快车的速度是x千米/时,根据快车速度×时间-慢车速度×时间=快车多行驶的距离,列出方程解答即可。
【详解】解:设快车的速度是x千米/时。
6x-95×6=60×2
6x-570=120
6x-570+570=120+570
6x=690
6x÷6=690÷6
x=115
答:快车的速度是115千米/时。
14.不能
【分析】根据实际距离=图上距离÷比例尺,据此求出亮亮家到某景点的实际距离,再根据路程÷速度=时间,据此求出亮亮家到某景点需要的时间,用7:00加上需要的时间即可求出到达景点的时间,最后与12:00对比即可。
【详解】10.5÷=10.5×4000000=42000000(厘米)
42000000厘米=420千米
420÷80=5.25(小时)=5时15分
7:00+5时15分=12时15分
答:12时15分到达景点,所以12:00不能赶到景点。
15.(1)25.2千米
(2)5.8厘米
【分析】(1)实际距离=图上距离÷比例尺,据此解答即可;
(2)图上距离=实际距离×比例尺,据此解答即可。
【详解】(1)8.4÷=2520000(厘米)
2520000厘米=25.2千米
答: 地铁1号线实际距离约25.2千米。
(2)17.4公里=17.4千米
17.4千米=1740000厘米
1740000×=5.8(厘米)
答:地铁4号线在这张地图上约5.8厘米。
【点睛】熟练掌握图上距离、实际距离、比例尺三者之间的关系是解答此题的关键。
16.30分钟
【分析】设跑完2号线全程大约需x分钟,根据路程∶时间=速度,列出正比例算式解答即可。
【详解】解:设跑完2号线全程大约需x分钟。
18.3∶x=6.1∶10
6.1x=18.3×10
6.1x=183
6.1x÷6.1=183÷6.1
x=30
答:跑完2号线全程大约需30分钟。
【点睛】关键是确定比例关系,比值一定是正比例关系。
17.80千米
【分析】根据路程÷速度=时间可知,相遇时间相同时,路程和速度成正比例关系,即客车与货车的路程之比等于它们的速度之比,据此列出比例方程,并求解。
【详解】解:设货车行驶了千米。
96∶=6∶5
6=96×5
6=480
6÷6=480÷6
=80
答:货车行驶了80千米。
【点睛】本题考查列比例方程解决问题,根据速度、时间、路程之间的关系,分析出路程和速度成正比例关系是解题的关键。
18.0.5小时
【分析】
根据实际距离=图上距离÷比例尺,将数据代入求出甲、乙两城之间的实际距离;
由低级单位厘米转化成高级单位千米,除以进率100000,将两地的实际距离转化成以千米为单位;
再根据时间=路程÷速度,将数据代入求出从甲城到乙城需要几小时。
【详解】由分析可得:
6÷=6×500000=3000000(厘米)
3000000厘米=3000000÷100000=30(千米)
30÷60=0.5(小时)
答:需要0.5小时到达。
19.270千米
【分析】根据实际距离=图上距离÷比例尺,用2.7÷即可求出榆林到延安的实际距离,再将单位换算成千米即可。
【详解】2.7÷
=2.7×10000000
=27000000(厘米)
27000000厘米=270千米
答:榆林到延安的实际距离是270千米。
20.45米
【分析】由题意可知,设水塔的高度是x米,根据同一时间,同一地点物体高度与它的影长成正比例,据此列比例解答即可。
【详解】解:设水塔的高度是x米。
1.5∶2=x∶60
2x=1.5×60
2x=90
2x÷2=90÷2
x=45
答:水塔的高度是45米。
21.11时
【分析】先根据“实际距离=图上距离÷比例尺”,用3.6÷求出实际距离是18000000厘米,即180千米。再根据“路程÷速度=时间”,用180÷60求出这辆汽车从甲地到乙地所用的时间;最后用出发的时间加上经过的时间求出到达的时间。
【详解】3.6÷
=3.6×5000000
=18000000(厘米)
18000000厘米=180千米
180÷60=3(小时)
8时+3小时=11时
答:这辆汽车到达乙地是11时。
22.20行
【分析】由题意可知,学生的总人数一定,则每行的人数和行数成反比例,据此解答即可。
【详解】解:设可以站x行,
30x=24×25
30x=600
30x÷30=600÷30
x=20
答:可以站20行。
23.6.5小时
【分析】根据速度=路程÷时间;根据题意,由于汽车的速度不变,前3小时行驶的速度与从甲地到乙地行驶的速度相等,设到达乙地一共需要x小时,列比例:240∶3=520∶x,解比例,即可解答。
【详解】解:设到达乙地一共需要x小时。
240∶3=520∶x
240x=520×3
240x=1560
x=1560÷240
x=6.5
答:到达乙地一共需要6.5小时。
24.560米
【分析】根据题意可知,铺路的长度∶天数=每天铺路的长度(一定),比值一定,则铺路的长度与天数成正比例关系,据此列出正比例方程,并求解。
【详解】解:设这条管道一共长米。
240∶6=∶(6+8)
6=240×(6+8)
6=240×14
6=3360
=3360÷6
=560
答:这条管道一共长560米。
25.(1)10米、6米和2米
(2)32米
(3)10分钟
【分析】(1)根据实际距离=图上距离÷比例尺,据此进行计算即可;
(2)由题意可知,警戒水位线的长度就是长方体的底面周长,根据长方形的周长公式:C=(a+b)×2,据此进行计算即可;
(3)根据题意,可依据长方体的体积公式:V=abh计算出这个水的体积,再依据圆柱的体积公式:V=πr2h计算出这根放水管的每秒钟放水的体积,再用水管的每秒钟放水的体积乘60即可得到水管每分钟放水的体积,用水的体积除以出水管每分钟放水的体积,注意结果要保留整数即可。
【详解】(1)5÷=5×200=1000(厘米)
1000厘米=10米
3÷=3×200=600(厘米)
600厘米=6米
1÷=1×200=200(厘米)
200厘米=2米
答:这个水池的长、宽、深各应挖10米、6米和2米。
(2)(10+6)×2
=16×2
=32(米)
答:警戒水位线全长32米。
(3)10×6×(2-0.6)
=10×6×1.4
=60×1.4
=84(立方米)
2分米=0.2米
3.14×(0.2÷2)2×4.5
=3.14×0.12×4.5
=3.14×0.01×4.5
=0.0314×4.5
=0.1413(立方米)
0.1413×60=8.478(立方米/分)
84÷8.478≈10(分钟)
答:放完池中警戒水位以下的水大约需要10分钟。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版小学数学六年级下册
第四单元《比例》单元专项训练——应用题
1.看图回答问题。
(1)香蕉的总价和购买的质量成正比例吗?苹果呢?
(2)从图像上看,苹果和香蕉哪种水果贵一些?你是怎么看出来的?
(3)利用图像估计一下,苹果、香蕉各买2.5千克的总价分别是多少元?
2.今年妈妈和小红的年龄比是5∶1,10年后妈妈和小红的年龄比是5∶2,今年妈妈和小红各多少岁?
3.在比例尺是1∶100的图纸上,量得学校会议室的长为30厘米,宽为12厘米。学校准备把会议室铺上边长为6分米的地砖,大约需要多少块这样的地砖?
4.王叔叔用180厘米长的铁丝围成一个长和宽的比是3∶2的长方形,然后用1∶9的比例尺,把这个长方形画到图纸上,这个长方形在图纸上的面积是多少平方厘米?
5.国家游泳中心“水立方”改造成“冰立方”,成为冬奥会历史上体量最大的冰壶场馆。冰壶场地是由长50米、宽25米、深约3米的泳池改造而成的,如果将这个泳池的平面图画在比例尺是1∶200的图纸上,长和宽各应画多少厘米?
6.按3∶1画出平行四边形A放大后得到的平行四边形B,再画出把平行四边形B按1∶2缩小后得到的平行四边形C。
(1)哪些图形是由平行四边形A放大后得到的?哪些图形是由平行四边形B缩小后得到的?
(2)观察平行四边形A和B,它们的面积有什么变化?面积与边长是按相同的比变化的吗?
7.一瓶消毒液的标签上写着:“将原液和清水按1∶400配置使用”,倒出原液4克,应加多少克清水?(用比例解答)
8.在比例尺为1∶5000000的地图上量的甲、乙两地的距离是12.6厘米,客车和货车分别从两地同时出发相向而行,5小时后两车相遇。已知客车的速度是每小时70千米,货车的速度是每小时多少千米?
9.在一幅地图上,用6厘米的距离表示实际距离1200千米。在这幅地图上量得A、B两地的距离是4.5厘米,A、B两地的实际距离是多少千米?一条560千米的高速公路,在这幅地图上是多少厘米?
10.一批桃子,如果每箱装30个,那么可以装12箱。如果每个箱子多装10个桃子,那么可以装多少箱?(用比例知识解答)
11.如图是比例尺为1∶100的圆形水池平面图,工人要在圆形水池的周围修一条宽是1米的环形小路,请画出这条小路,并计算环形小路的面积。
12.下面是某市人民路路段的部分平面图。
(1)超市在公园( )面,距离公园( )米处。
(2)小艺家在公园( )偏( )( )°方向,距离公园( )米处。
(3)公园东面1500米处,有一条与人民路垂直且长度差不多的共和路,在图中画线段表示共和路。
(4)小艺乘出租车沿图中所示的路线从家到超市,按以下收费标准她需要支付多少车费?
某市出租车收费标准
里程 收费
2km及以下 9元
2km以上每增加1km(不足1km按1km计算) 1.9元
13.在一幅比例尺是1∶9000000的地图上,量得京沪高速公路的全长是14厘米,两辆汽车分别同时从北京和上海出发相向而行,6小时后两车在距两地中点60千米处相遇。已知慢车的速度是95千米/时,快车的速度是多少?
14.在一幅比例尺是1∶4000000的地图上,量得亮亮家到某景点的距离是10.5厘米。如果他们7:00自驾从家出发,以80千米/时的平均速度行驶,12:00能赶到景点吗?
15.下图是洛阳地铁1号线,它覆盖洛北地区东西方向主要客流,连接涧西、西工、老城、瀍河4个城市区。下图比例尺是1∶300000,地铁1号线的图上距离约为8.4厘米。
(1)请计算出地铁1号线实际距离约为多少千米?
(2)计划开建的洛阳地铁4号线全长17.4公里,地铁4号线在这张地图上约多少厘米?
16.洛阳地铁2号线整条线路全长约18.3千米,地铁列车10分钟大约可运行6.1千米,照这样计算,跑完2号线全程大约需多少分钟?(用比例解)
17.一辆客车和一辆货车同时从A、B两地相对开出,它们的速度之比是6∶5,相遇时客车行驶了96千米,货车行驶了多少千米?(用比例解答)
18.在比例尺是1∶500000的地图上,量得甲、乙两城之间的距离是6厘米。一辆汽车从甲城到乙城,每小时行60千米,需要几小时到达?
19.在一幅比例尺是1∶10000000的地图上,量得榆林到延安的图上距离是2.7厘米,榆林到延安的实际距离是多少?
20.琪琪身高1.5米,阳光下她的影长为2米,此时测得一个水塔在同一地面的影长为60米,水塔的高度是几米?
21.在比例尺是1∶5000000的地图上,量得甲地到乙地的距离是3.6厘米。一辆汽车上午8时以每小时60千米的速度从甲地出发,这辆汽车到达乙地是几时?
22.为庆祝六一儿童节,实验小学举行团体操表演,如果每行站25人,那么正好站24行;如果每行站30人,那么可以站多少行?(用比例知识解答)
23.甲、乙两地相距520千米。一辆汽车从甲地出发开往乙地,前3小时行驶了240千米。照这样的速度,到达乙地一共需要多少小时?(用比例解)
24.某工程队铺一条管道,前6天铺了240米,照这样计算,还要8天才能把管道铺完,这条管道一共长多少米?(用比例知识解答)
25.学校要挖一个长方体泳池,在比例尺是1∶200的设计图上,水池的长为5厘米,宽为3厘米,深为1厘米。
(1)按图施工,这个水池的长、宽、深各应挖多少米?
(2)沿泳池内壁距池口0.6米处用红漆画一条警戒水位线,警戒水位线全长多少米?
(3)池底有根排水管,内直径2分米,放水时,水流速度平均每秒4.5米。放完池中警戒水位以下的水大约需要多少分钟?(结果保留整数)
参考答案:
1.(1)香蕉的总价和购买的质量成正比例;苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;由图像可知,1千克香蕉8元,1千克苹果4元,所以香蕉贵一些。
(3)苹果总价10元;香蕉总价20元。
【分析】(1)总价÷数量=单价,选择几组数据计算香蕉和苹果的单价 ,如果单价一定,则总价和购买的质量成正比例;
(2)有2种方法:①观察同样的质量,对比总价,哪种的总价更高,则哪种水果更贵;②同样的总价,对比质量,哪种的质量更少,则哪种水果更贵;(合理即可,答案不唯一)
(3)观察图像可知,1千克苹果4元,1千克香蕉8元,总价=单价×数量,代入数据计算即可。
【详解】(1)香蕉:(元)
(元)
(元)
香蕉的单价为每千克8元(一定),所以香蕉的总价和购买的质量成正比例。
苹果:(元)
(元)
(元)
苹果的单价为每千克4元(一定),所以苹果的总价和购买的质量成正比例。
(2)香蕉贵一些;观察图像可知,1千克苹果4元,1千克香蕉8元,所以香蕉贵一些。(合理即可,答案不唯一)
(3)苹果:(元)
香蕉:(元)
答:2.5千克苹果的总价为10元,2.5千克香蕉的总价为20元。
2.30岁;6岁
【分析】
由题意可知,设小红今年的年龄是x岁,则妈妈今年的年龄是5x岁,10年后小红的年龄为(x+10)岁,妈妈的年龄为(5x+10)岁,再结合10年后妈妈和小红的年龄比是5∶2,据此列比例解答即可。
【详解】
解:设小红今年的年龄是x岁,则妈妈今年的年龄是5x岁。
(5x+10)∶(x+10)=5∶2
5×(x+10)=2×(5x+10)
5x+50=10x+20
5x+50-5x=10x+20-5x
5x+20=50
5x+20-20=50-20
5x=30
x=30÷5
x=6
5×6=30(岁)
答:今年妈妈30岁,小红6岁。
3.1000块
【分析】
根据实际距离=图上距离÷比例尺,代入数据分别求出该会议室的长和宽的实际厘米数,由低级单位厘米转换成高级单位分米,除以进率10,据此将长和宽的实际厘米数转换成以分米为单位;
根据长方形面积=长×宽,代入数据求出会议室的面积,再根据正方形面积=边长×边长,代入数据求出地砖的面积,最后用会议室的面积除以地砖的面积即可求出需要几块这样的地砖。
【详解】
由分析可得:
30×100=3000(厘米)
3000厘米=3000÷10=300(分米)
12×100=1200(厘米)
1200厘米=1200÷10=120(分米)
300×120÷(6×6)
=300×120÷36
=36000÷36
=1000(块)
答:大约需要1000块这样的地砖。
4.24平方厘米
【分析】
长方形的周长等于两条长和两条宽的和,用180除以2,可得该长方形一条长和一条宽的和,因为长和宽的比是3∶2,将一条长和一条宽的和看作单位“1”,根据分数乘法的意义,求一个数的几分之几是多少用乘法,即分别用单位“1”乘和可求出长方形实际的长和宽各是多少厘米;
再根据图上距离=实际距离×比例尺,用求出的长和宽分别乘比例尺,即可求出长方形在图纸上的长和宽分别是多少厘米;
最后根据长方形面积=长×宽,代入数据求出长方形图上的面积即可。
【详解】
由分析可得:
180÷2=90(厘米)
长:(厘米)
宽:(厘米)
(厘米)
(厘米)
6×4=24(平方厘米)
答:这个长方形在图纸上的面积是24平方厘米。
5.25厘米;12.5厘米
【分析】将这个泳池的平面图画在比例尺是1∶200的图纸上,也就是将实际长度缩短到原来的,用实际长度乘,就是图纸上的长度。据此解答。
【详解】
50米=5000厘米
25米=2500厘米
5000×=25(厘米)
2500×=12.5(厘米)
答:长应画25厘米,宽应画12.5厘米。
6.
见详解
【分析】按3∶1放大,就是放大到原图面积的3倍,将平行四边形A的底放大到6,高放大到6,就是放大的图形B;
按1∶2缩小就是缩小到原来的,将图形B的底缩小到 3、高缩小到3就得到图形C。
【详解】
(1)图形B和C是图形A放大后得到的;图形A和图形C是图形B缩小后得到的。
(2)图形A:2×2=4;图形B:6×6=36;36÷4=9
图形B面积是图形A面积的9倍,面积与边长不是按相同的比变化的。
7.1600克
【分析】根据题意可知,原液的质量∶清水的质量=1∶400,据此列出比例方程,并求解。
【详解】解:设应加克清水。
4∶=1∶400
×1=4×400
=1600
答:应加1600克清水。
8.56千米
【分析】根据实际距离=图上距离÷比例尺,据此求出甲、乙两地的实际距离;然后设货车的速度是每小时x千米,再根据相遇问题中的等量关系:速度和×相遇时间=路程和,据此列方程解答即可。
【详解】解:设货车的速度是每小时x千米。
12.6÷=12.6×5000000=63000000(厘米)
63000000厘米=630千米
(70+x)×5=630
(70+x)×5÷5=630÷5
70+x=126
70+x-70=126-70
x=56
答:货车的速度是每小时56千米。
9.900千米;2.8厘米
【分析】根据比例尺=图上距离∶实际距离,据此求出这幅地图的比例尺,再根据实际距离=图上距离÷比例尺,据此计算可求出A、B两地的实际距离;根据图上距离=实际距离×比例尺,据此可求出一条560千米的高速公路,在这幅地图上是多少厘米。
【详解】6厘米∶1200千米
=6厘米∶120000000厘米
=6∶120000000
=(6÷6)∶(120000000÷6)
=1∶20000000
4.5÷=4.5×20000000=90000000(厘米)
90000000厘米=900千米
560千米=56000000厘米
56000000×=2.8(厘米)
答:A、B两地的实际距离是900千米,一条560千米的高速公路,在这幅地图上是2.8厘米。
10.9箱
【分析】由题意可知,设可以装x箱,这批桃子的数量一定,则每箱装的个数与箱数成反比例关系,据此列比例解答即可。
【详解】解:设可以装x箱。
30×12=(30+10)x
40x=360
40x÷40=360÷40
x=9
答:可以装9箱。
11.画图见详解;9.42平方米
【分析】画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
根据图上距离=实际距离×比例尺,求出小路图上宽,测量出水池图上半径,小路宽+水池半径=大圆半径,据此根据画圆的方法画出小路。
根据实际距离=图上距离÷比例尺,确定大圆和小圆半径,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】测量可知,一格长1厘米,即圆形水池半径图上1厘米。
1米=100厘米
100×=1(厘米)
1+1=2(厘米)
1÷=1×100=100(厘米)=1(米)
2÷=2×100=200(厘米)=2(米)
3.14×(22-12)
=3.14×(4-1)
=3.14×3
=9.42(平方米)
答:环形小路的面积是9.42平方米。
12.(1)东;2700
(2)北;西;30;1800
(3)见详解
(4)14.7元
【分析】(1)经过测量得到,公园到超市的图上距离是2.7厘米,根据“实际距离=图上距离÷比例尺”可以计算出实际距离,图上的方向是上北下南,左西右东,据此得到超市在公园东面;
(2)应用方位角表示位置,要确定方向和距离。首先根据公园到小艺家的图上距离是1.8厘米,计算出实际距离,再用“方向+偏移角度”表示即可;
(3)计算出实际距离是1500米的图上距离,也就确定了共和路与人民路的交点,再在交点处画出垂直于人民路的共和路(长度与人民路差不多)即可;
(4)根据(1)、(2)计算出从家到超市的实际距离,对照收费标准,看看计费里程约是多少,按照收费标准计算车费。
【详解】(1)(厘米)=2700(米)
超市在公园东面,距离公园2700米处。
(2)(厘米)=1800(米)
小艺家在公园北偏西30°(西偏北60°)方向,距离公园1800米处。
(3)(米)=1.5(厘米)
(4)(米)=4.5(千米)
(千米)
(元)
答:她需要支付14.7元车费。
13.115千米/时
【分析】两车在距两地中点60千米处相遇,说明相遇时,快车比慢车多行驶(60×2)千米,设快车的速度是x千米/时,根据快车速度×时间-慢车速度×时间=快车多行驶的距离,列出方程解答即可。
【详解】解:设快车的速度是x千米/时。
6x-95×6=60×2
6x-570=120
6x-570+570=120+570
6x=690
6x÷6=690÷6
x=115
答:快车的速度是115千米/时。
14.不能
【分析】根据实际距离=图上距离÷比例尺,据此求出亮亮家到某景点的实际距离,再根据路程÷速度=时间,据此求出亮亮家到某景点需要的时间,用7:00加上需要的时间即可求出到达景点的时间,最后与12:00对比即可。
【详解】10.5÷=10.5×4000000=42000000(厘米)
42000000厘米=420千米
420÷80=5.25(小时)=5时15分
7:00+5时15分=12时15分
答:12时15分到达景点,所以12:00不能赶到景点。
15.(1)25.2千米
(2)5.8厘米
【分析】(1)实际距离=图上距离÷比例尺,据此解答即可;
(2)图上距离=实际距离×比例尺,据此解答即可。
【详解】(1)8.4÷=2520000(厘米)
2520000厘米=25.2千米
答: 地铁1号线实际距离约25.2千米。
(2)17.4公里=17.4千米
17.4千米=1740000厘米
1740000×=5.8(厘米)
答:地铁4号线在这张地图上约5.8厘米。
【点睛】熟练掌握图上距离、实际距离、比例尺三者之间的关系是解答此题的关键。
16.30分钟
【分析】设跑完2号线全程大约需x分钟,根据路程∶时间=速度,列出正比例算式解答即可。
【详解】解:设跑完2号线全程大约需x分钟。
18.3∶x=6.1∶10
6.1x=18.3×10
6.1x=183
6.1x÷6.1=183÷6.1
x=30
答:跑完2号线全程大约需30分钟。
【点睛】关键是确定比例关系,比值一定是正比例关系。
17.80千米
【分析】根据路程÷速度=时间可知,相遇时间相同时,路程和速度成正比例关系,即客车与货车的路程之比等于它们的速度之比,据此列出比例方程,并求解。
【详解】解:设货车行驶了千米。
96∶=6∶5
6=96×5
6=480
6÷6=480÷6
=80
答:货车行驶了80千米。
【点睛】本题考查列比例方程解决问题,根据速度、时间、路程之间的关系,分析出路程和速度成正比例关系是解题的关键。
18.0.5小时
【分析】
根据实际距离=图上距离÷比例尺,将数据代入求出甲、乙两城之间的实际距离;
由低级单位厘米转化成高级单位千米,除以进率100000,将两地的实际距离转化成以千米为单位;
再根据时间=路程÷速度,将数据代入求出从甲城到乙城需要几小时。
【详解】由分析可得:
6÷=6×500000=3000000(厘米)
3000000厘米=3000000÷100000=30(千米)
30÷60=0.5(小时)
答:需要0.5小时到达。
19.270千米
【分析】根据实际距离=图上距离÷比例尺,用2.7÷即可求出榆林到延安的实际距离,再将单位换算成千米即可。
【详解】2.7÷
=2.7×10000000
=27000000(厘米)
27000000厘米=270千米
答:榆林到延安的实际距离是270千米。
20.45米
【分析】由题意可知,设水塔的高度是x米,根据同一时间,同一地点物体高度与它的影长成正比例,据此列比例解答即可。
【详解】解:设水塔的高度是x米。
1.5∶2=x∶60
2x=1.5×60
2x=90
2x÷2=90÷2
x=45
答:水塔的高度是45米。
21.11时
【分析】先根据“实际距离=图上距离÷比例尺”,用3.6÷求出实际距离是18000000厘米,即180千米。再根据“路程÷速度=时间”,用180÷60求出这辆汽车从甲地到乙地所用的时间;最后用出发的时间加上经过的时间求出到达的时间。
【详解】3.6÷
=3.6×5000000
=18000000(厘米)
18000000厘米=180千米
180÷60=3(小时)
8时+3小时=11时
答:这辆汽车到达乙地是11时。
22.20行
【分析】由题意可知,学生的总人数一定,则每行的人数和行数成反比例,据此解答即可。
【详解】解:设可以站x行,
30x=24×25
30x=600
30x÷30=600÷30
x=20
答:可以站20行。
23.6.5小时
【分析】根据速度=路程÷时间;根据题意,由于汽车的速度不变,前3小时行驶的速度与从甲地到乙地行驶的速度相等,设到达乙地一共需要x小时,列比例:240∶3=520∶x,解比例,即可解答。
【详解】解:设到达乙地一共需要x小时。
240∶3=520∶x
240x=520×3
240x=1560
x=1560÷240
x=6.5
答:到达乙地一共需要6.5小时。
24.560米
【分析】根据题意可知,铺路的长度∶天数=每天铺路的长度(一定),比值一定,则铺路的长度与天数成正比例关系,据此列出正比例方程,并求解。
【详解】解:设这条管道一共长米。
240∶6=∶(6+8)
6=240×(6+8)
6=240×14
6=3360
=3360÷6
=560
答:这条管道一共长560米。
25.(1)10米、6米和2米
(2)32米
(3)10分钟
【分析】(1)根据实际距离=图上距离÷比例尺,据此进行计算即可;
(2)由题意可知,警戒水位线的长度就是长方体的底面周长,根据长方形的周长公式:C=(a+b)×2,据此进行计算即可;
(3)根据题意,可依据长方体的体积公式:V=abh计算出这个水的体积,再依据圆柱的体积公式:V=πr2h计算出这根放水管的每秒钟放水的体积,再用水管的每秒钟放水的体积乘60即可得到水管每分钟放水的体积,用水的体积除以出水管每分钟放水的体积,注意结果要保留整数即可。
【详解】(1)5÷=5×200=1000(厘米)
1000厘米=10米
3÷=3×200=600(厘米)
600厘米=6米
1÷=1×200=200(厘米)
200厘米=2米
答:这个水池的长、宽、深各应挖10米、6米和2米。
(2)(10+6)×2
=16×2
=32(米)
答:警戒水位线全长32米。
(3)10×6×(2-0.6)
=10×6×1.4
=60×1.4
=84(立方米)
2分米=0.2米
3.14×(0.2÷2)2×4.5
=3.14×0.12×4.5
=3.14×0.01×4.5
=0.0314×4.5
=0.1413(立方米)
0.1413×60=8.478(立方米/分)
84÷8.478≈10(分钟)
答:放完池中警戒水位以下的水大约需要10分钟。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
