18.2.2.1 菱形的性质同步练习(含答案)
文档属性
| 名称 | 18.2.2.1 菱形的性质同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 17:26:58 | ||
图片预览

文档简介
18.1 平行四边形
18.2.2 菱形
第1课时 菱形的性质
一、选择题
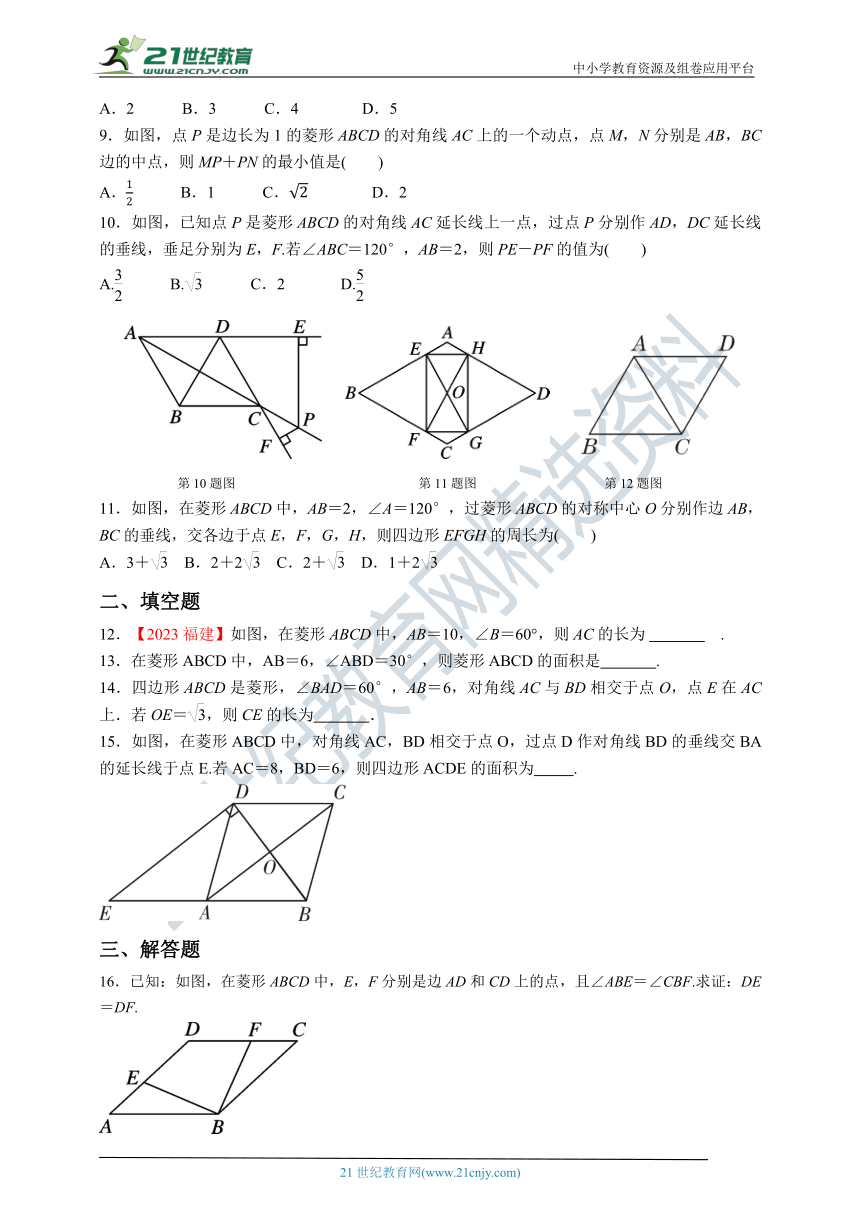
1.【2023大庆】将两个完全相同的菱形按如图方式放置,若∠BAD=α,∠CBE=β,则β=( )
A.45°+α B.45°+α C.90°-α D.90°-α
第1题图 第2题图 第4题图
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.若OE=3,则AB的长是( )
A.6 B.5 C.4 D.3
3.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等 C.对角线互相垂直 D.是轴对称图形
4.如图,在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE=( )
A.70° B.40° C.75° D.30°
5.菱形ABCD的对角线AC=10,BD=8,则菱形ABCD的面积是( )
A.80 B.60 C.40 D.30
6.若菱形的周长为16,高为2,则菱形的面积为( )
A.4 B.6 C.8 D.32
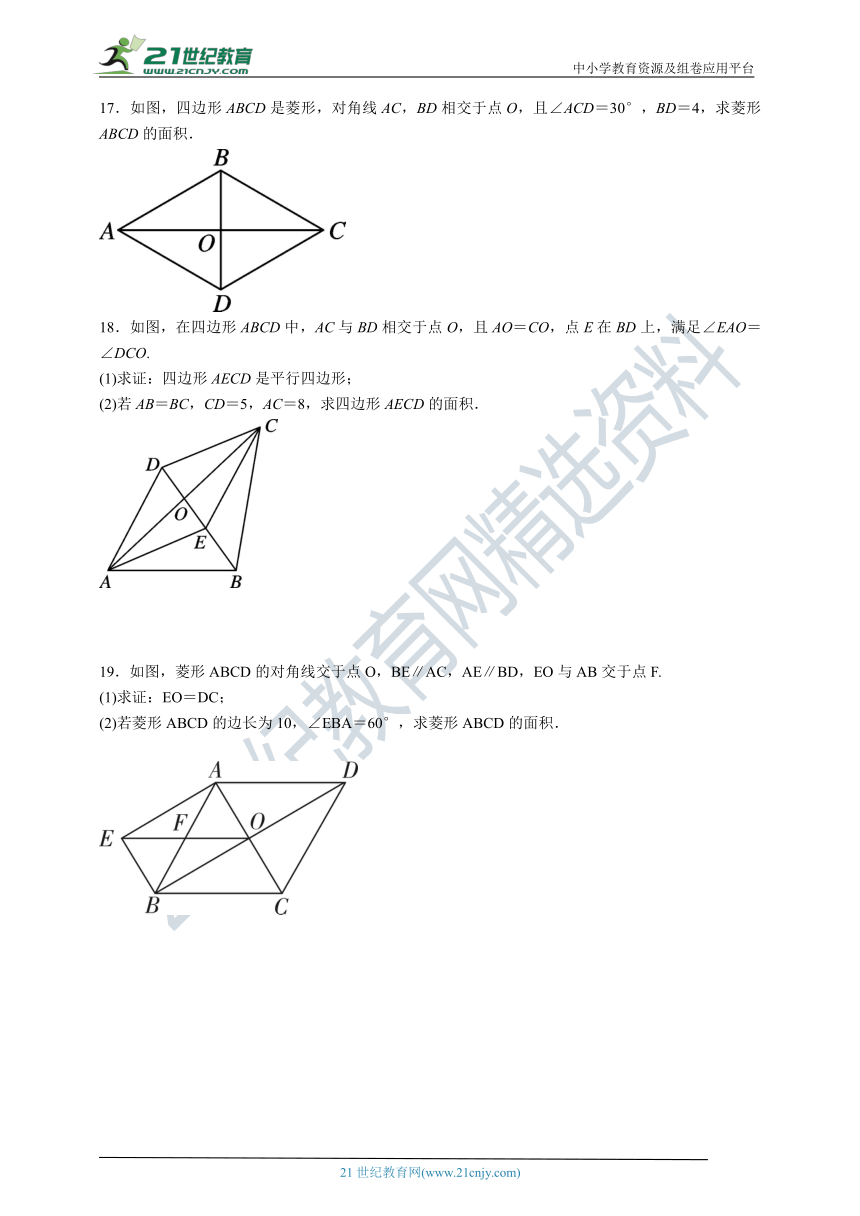
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
第7题图 第8题图 第9题图
8.如图,在菱形ABCD中,点E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )
A.2 B.3 C.4 D.5
9.如图,点P是边长为1的菱形ABCD的对角线AC上的一个动点,点M,N分别是AB,BC边的中点,则MP+PN的最小值是( )
A. B.1 C. D.2
10.如图,已知点P是菱形ABCD的对角线AC延长线上一点,过点P分别作AD,DC延长线的垂线,垂足分别为E,F.若∠ABC=120°,AB=2,则PE-PF的值为( )
A. B. C.2 D.
第10题图 第11题图 第12题图
11.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A.3+ B.2+2 C.2+ D.1+2
二、填空题
12.【2023福建】如图,在菱形ABCD中,AB=10,∠B=60°,则AC的长为 .
13.在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是 .
14.四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上.若OE=,则CE的长为 .
15.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.若AC=8,BD=6,则四边形ACDE的面积为 .
三、解答题
16.已知:如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
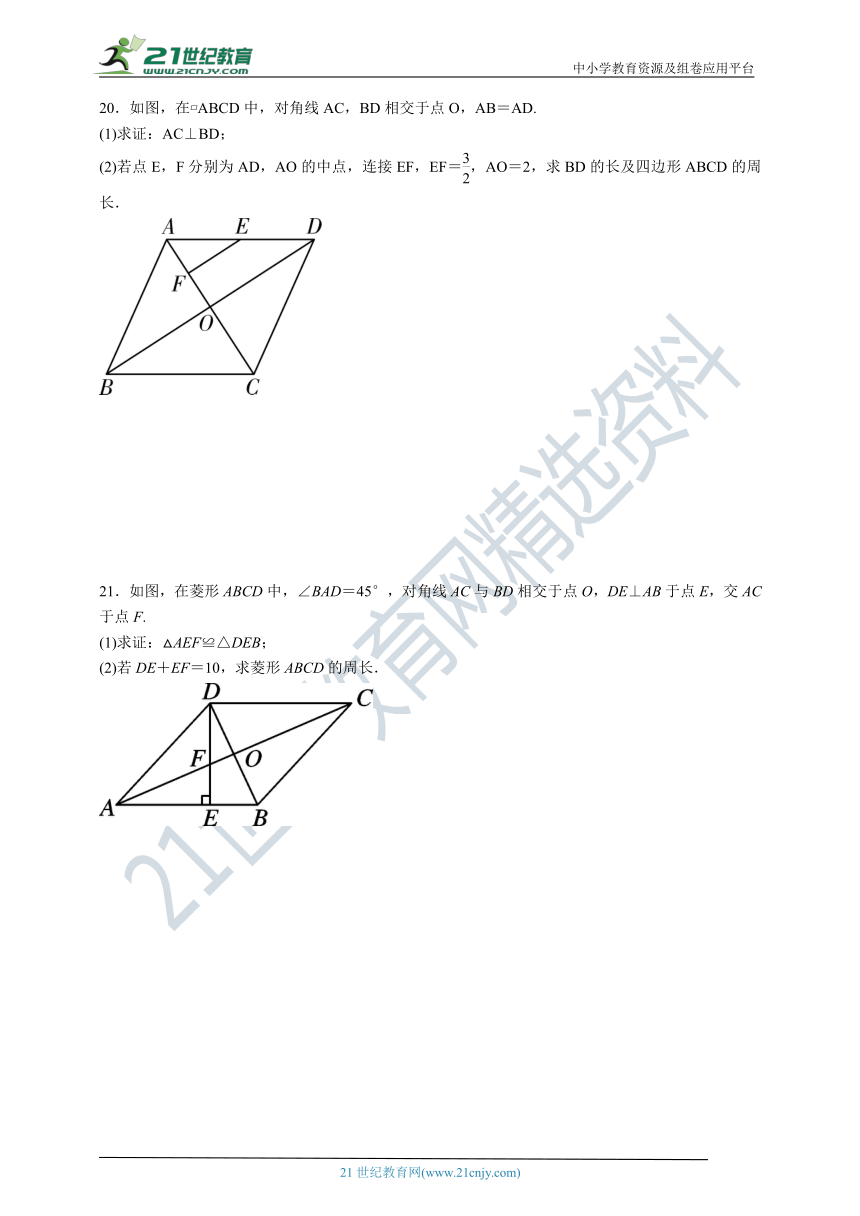
17.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
18.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
19.如图,菱形ABCD的对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.
20.如图,在 ABCD中,对角线AC,BD相交于点O,AB=AD.
(1)求证:AC⊥BD;
(2)若点E,F分别为AD,AO的中点,连接EF,EF=,AO=2,求BD的长及四边形ABCD的周长.
21.如图,在菱形ABCD中,∠BAD=45°,对角线AC与BD相交于点O,DE⊥AB于点E,交AC于点F.
(1)求证:△AEF≌△DEB;
(2)若DE+EF=10,求菱形ABCD的周长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
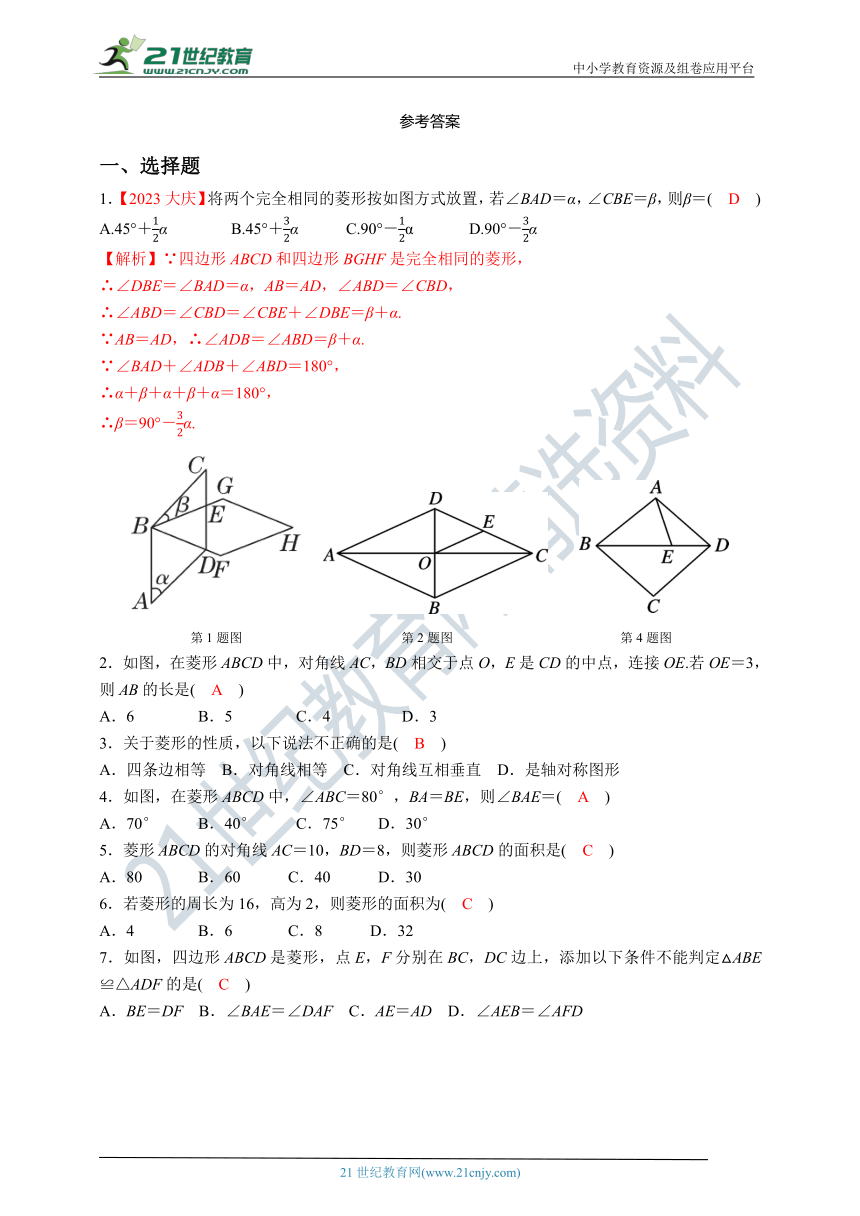
1.【2023大庆】将两个完全相同的菱形按如图方式放置,若∠BAD=α,∠CBE=β,则β=( D )
A.45°+α B.45°+α C.90°-α D.90°-α
【解析】∵四边形ABCD和四边形BGHF是完全相同的菱形,
∴∠DBE=∠BAD=α,AB=AD,∠ABD=∠CBD,
∴∠ABD=∠CBD=∠CBE+∠DBE=β+α.
∵AB=AD,∴∠ADB=∠ABD=β+α.
∵∠BAD+∠ADB+∠ABD=180°,
∴α+β+α+β+α=180°,
∴β=90°-α.
第1题图 第2题图 第4题图
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.若OE=3,则AB的长是( A )
A.6 B.5 C.4 D.3
3.关于菱形的性质,以下说法不正确的是( B )
A.四条边相等 B.对角线相等 C.对角线互相垂直 D.是轴对称图形
4.如图,在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE=( A )
A.70° B.40° C.75° D.30°
5.菱形ABCD的对角线AC=10,BD=8,则菱形ABCD的面积是( C )
A.80 B.60 C.40 D.30
6.若菱形的周长为16,高为2,则菱形的面积为( C )
A.4 B.6 C.8 D.32
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( C )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
第7题图 第8题图 第9题图
8.如图,在菱形ABCD中,点E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( B )
A.2 B.3 C.4 D.5
9.如图,点P是边长为1的菱形ABCD的对角线AC上的一个动点,点M,N分别是AB,BC边的中点,则MP+PN的最小值是( B )
A. B.1 C. D.2
【解析】如图,取AD的中点M ',连接M'N,M'P,则有MP=M'P.所以MP+PN的最小值为线段M'N的长,即菱形的边长.
10.如图,已知点P是菱形ABCD的对角线AC延长线上一点,过点P分别作AD,DC延长线的垂线,垂足分别为E,F.若∠ABC=120°,AB=2,则PE-PF的值为( B )
A. B. C.2 D.
第10题图 第11题图 第12题图
11.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( A )
A.3+ B.2+2 C.2+ D.1+2
【解析】如图,连接BD,AC.由题意及菱形的性质证得△BEF,
△DHG,△OEH和△OFG均为等边三角形,由AB=2,∠A=120°,可求得BE=EF=GH=,EH=FG=,∴四边形EFGH的周长为3+.
二、填空题
12.【2023福建】如图,在菱形ABCD中,AB=10,∠B=60°,则AC的长为 .
【答案】10
【解析】由菱形的性质得到AB=BC,又∠B=60°,∴△ABC是等边三角形,∴AC=AB=10.
13.在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是 .
【答案】18
14.四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上.若OE=,则CE的长为 .
【答案】4或2
15.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.若AC=8,BD=6,则四边形ACDE的面积为 .
【答案】24
三、解答题
16.已知:如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
证明:∵四边形ABCD是菱形,
∴AD=CD=AB=BC,∠A=∠C,
又∵∠ABE=∠CBF,
∴△ABE≌△CBF(ASA),
∴AE=CF,
∴AD-AE=CD-CF,
∴DE=DF.
17.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
解:由题意,得OD=2,CD=4,
∴OC==2 ,
∴AC=4,
∴S菱形ABCD=×4×4=8.
18.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
解:(1)证明:在△AOE和△COD中,
∴△AOE≌△COD(ASA),∴OD=OE,
又∵AO=CO,∴四边形AECD是平行四边形.
(2)∵AB=BC,AO=CO,∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,∴CO=AC=4,
在Rt△COD中,由勾股定理,得
OD==3,∴DE=2OD=6,
∴菱形AECD的面积为AC·DE=×8×6=24.
19.如图,菱形ABCD的对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.
(1)证明:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O,∴AC⊥BD,即∠AOB=90°,
∴四边形AEBO是矩形,∴EO=AB.
在菱形ABCD中,AB=DC,∴EO=DC.
(2)解:由(1)知四边形AEBO是矩形.
∴∠EBO=90°.∵∠EBA=60°,∴∠ABO=30°.
在Rt△ABO中,AB=10,∠ABO=30°,
∴AO=5,BO==5,∴BD=10,
∴菱形ABCD的面积
=△ABD的面积+△BCD的面积
=2×△ABD的面积=2××10×5=50.
20.如图,在 ABCD中,对角线AC,BD相交于点O,AB=AD.
(1)求证:AC⊥BD;
(2)若点E,F分别为AD,AO的中点,连接EF,EF=,AO=2,求BD的长及四边形ABCD的周长.
(1)证明:∵四边形ABCD是平行四边,AB=AD,
∴四边形ABCD是菱形,
∴AC⊥BD.
(2)解:∵点E,F分别为AD,AO的中点,
∴EF是△AOD的中位线,∴EF=OD,∵EF=,∴OD=3,
∵四边形ABCD是菱形,∴BD=2OD=6,
由(1)知AC⊥BD,在Rt△AOD中,AO=2,OD=3,
∴AD===,
∴菱形ABCD的周长为4.
21.如图,在菱形ABCD中,∠BAD=45°,对角线AC与BD相交于点O,DE⊥AB于点E,交AC于点F.
(1)求证:△AEF≌△DEB;
(2)若DE+EF=10,求菱形ABCD的周长.
解:(1)证明:∵DE⊥AB,
∴∠AED=∠DEB=90°,
∵∠BAD=45°,∴∠ADE=∠BAD=45°,
∴AE=DE,
∵四边形ABCD是菱形,∴AC⊥BD,
∴∠OAB+∠ABD=∠BDE+∠ABD=90°,
∴∠OAB=∠BDE,
在△AEF和△DEB中,
∴△AEF≌△DEB(ASA).
(2)由(1)知,△AEF≌△DEB,∴EF=EB,
∴AB=AE+EB=DE+EF=10,
∵四边形ABCD是菱形,
∴菱形ABCD的周长为4AB=4×10=40.
18.2.2 菱形
第1课时 菱形的性质
一、选择题
1.【2023大庆】将两个完全相同的菱形按如图方式放置,若∠BAD=α,∠CBE=β,则β=( )
A.45°+α B.45°+α C.90°-α D.90°-α
第1题图 第2题图 第4题图
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.若OE=3,则AB的长是( )
A.6 B.5 C.4 D.3
3.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等 C.对角线互相垂直 D.是轴对称图形
4.如图,在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE=( )
A.70° B.40° C.75° D.30°
5.菱形ABCD的对角线AC=10,BD=8,则菱形ABCD的面积是( )
A.80 B.60 C.40 D.30
6.若菱形的周长为16,高为2,则菱形的面积为( )
A.4 B.6 C.8 D.32
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
第7题图 第8题图 第9题图
8.如图,在菱形ABCD中,点E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )
A.2 B.3 C.4 D.5
9.如图,点P是边长为1的菱形ABCD的对角线AC上的一个动点,点M,N分别是AB,BC边的中点,则MP+PN的最小值是( )
A. B.1 C. D.2
10.如图,已知点P是菱形ABCD的对角线AC延长线上一点,过点P分别作AD,DC延长线的垂线,垂足分别为E,F.若∠ABC=120°,AB=2,则PE-PF的值为( )
A. B. C.2 D.
第10题图 第11题图 第12题图
11.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A.3+ B.2+2 C.2+ D.1+2
二、填空题
12.【2023福建】如图,在菱形ABCD中,AB=10,∠B=60°,则AC的长为 .
13.在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是 .
14.四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上.若OE=,则CE的长为 .
15.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.若AC=8,BD=6,则四边形ACDE的面积为 .
三、解答题
16.已知:如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
17.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
18.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
19.如图,菱形ABCD的对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.
20.如图,在 ABCD中,对角线AC,BD相交于点O,AB=AD.
(1)求证:AC⊥BD;
(2)若点E,F分别为AD,AO的中点,连接EF,EF=,AO=2,求BD的长及四边形ABCD的周长.
21.如图,在菱形ABCD中,∠BAD=45°,对角线AC与BD相交于点O,DE⊥AB于点E,交AC于点F.
(1)求证:△AEF≌△DEB;
(2)若DE+EF=10,求菱形ABCD的周长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2023大庆】将两个完全相同的菱形按如图方式放置,若∠BAD=α,∠CBE=β,则β=( D )
A.45°+α B.45°+α C.90°-α D.90°-α
【解析】∵四边形ABCD和四边形BGHF是完全相同的菱形,
∴∠DBE=∠BAD=α,AB=AD,∠ABD=∠CBD,
∴∠ABD=∠CBD=∠CBE+∠DBE=β+α.
∵AB=AD,∴∠ADB=∠ABD=β+α.
∵∠BAD+∠ADB+∠ABD=180°,
∴α+β+α+β+α=180°,
∴β=90°-α.
第1题图 第2题图 第4题图
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.若OE=3,则AB的长是( A )
A.6 B.5 C.4 D.3
3.关于菱形的性质,以下说法不正确的是( B )
A.四条边相等 B.对角线相等 C.对角线互相垂直 D.是轴对称图形
4.如图,在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE=( A )
A.70° B.40° C.75° D.30°
5.菱形ABCD的对角线AC=10,BD=8,则菱形ABCD的面积是( C )
A.80 B.60 C.40 D.30
6.若菱形的周长为16,高为2,则菱形的面积为( C )
A.4 B.6 C.8 D.32
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( C )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
第7题图 第8题图 第9题图
8.如图,在菱形ABCD中,点E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( B )
A.2 B.3 C.4 D.5
9.如图,点P是边长为1的菱形ABCD的对角线AC上的一个动点,点M,N分别是AB,BC边的中点,则MP+PN的最小值是( B )
A. B.1 C. D.2
【解析】如图,取AD的中点M ',连接M'N,M'P,则有MP=M'P.所以MP+PN的最小值为线段M'N的长,即菱形的边长.
10.如图,已知点P是菱形ABCD的对角线AC延长线上一点,过点P分别作AD,DC延长线的垂线,垂足分别为E,F.若∠ABC=120°,AB=2,则PE-PF的值为( B )
A. B. C.2 D.
第10题图 第11题图 第12题图
11.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( A )
A.3+ B.2+2 C.2+ D.1+2
【解析】如图,连接BD,AC.由题意及菱形的性质证得△BEF,
△DHG,△OEH和△OFG均为等边三角形,由AB=2,∠A=120°,可求得BE=EF=GH=,EH=FG=,∴四边形EFGH的周长为3+.
二、填空题
12.【2023福建】如图,在菱形ABCD中,AB=10,∠B=60°,则AC的长为 .
【答案】10
【解析】由菱形的性质得到AB=BC,又∠B=60°,∴△ABC是等边三角形,∴AC=AB=10.
13.在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是 .
【答案】18
14.四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上.若OE=,则CE的长为 .
【答案】4或2
15.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.若AC=8,BD=6,则四边形ACDE的面积为 .
【答案】24
三、解答题
16.已知:如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
证明:∵四边形ABCD是菱形,
∴AD=CD=AB=BC,∠A=∠C,
又∵∠ABE=∠CBF,
∴△ABE≌△CBF(ASA),
∴AE=CF,
∴AD-AE=CD-CF,
∴DE=DF.
17.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
解:由题意,得OD=2,CD=4,
∴OC==2 ,
∴AC=4,
∴S菱形ABCD=×4×4=8.
18.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
解:(1)证明:在△AOE和△COD中,
∴△AOE≌△COD(ASA),∴OD=OE,
又∵AO=CO,∴四边形AECD是平行四边形.
(2)∵AB=BC,AO=CO,∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,∴CO=AC=4,
在Rt△COD中,由勾股定理,得
OD==3,∴DE=2OD=6,
∴菱形AECD的面积为AC·DE=×8×6=24.
19.如图,菱形ABCD的对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.
(1)证明:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O,∴AC⊥BD,即∠AOB=90°,
∴四边形AEBO是矩形,∴EO=AB.
在菱形ABCD中,AB=DC,∴EO=DC.
(2)解:由(1)知四边形AEBO是矩形.
∴∠EBO=90°.∵∠EBA=60°,∴∠ABO=30°.
在Rt△ABO中,AB=10,∠ABO=30°,
∴AO=5,BO==5,∴BD=10,
∴菱形ABCD的面积
=△ABD的面积+△BCD的面积
=2×△ABD的面积=2××10×5=50.
20.如图,在 ABCD中,对角线AC,BD相交于点O,AB=AD.
(1)求证:AC⊥BD;
(2)若点E,F分别为AD,AO的中点,连接EF,EF=,AO=2,求BD的长及四边形ABCD的周长.
(1)证明:∵四边形ABCD是平行四边,AB=AD,
∴四边形ABCD是菱形,
∴AC⊥BD.
(2)解:∵点E,F分别为AD,AO的中点,
∴EF是△AOD的中位线,∴EF=OD,∵EF=,∴OD=3,
∵四边形ABCD是菱形,∴BD=2OD=6,
由(1)知AC⊥BD,在Rt△AOD中,AO=2,OD=3,
∴AD===,
∴菱形ABCD的周长为4.
21.如图,在菱形ABCD中,∠BAD=45°,对角线AC与BD相交于点O,DE⊥AB于点E,交AC于点F.
(1)求证:△AEF≌△DEB;
(2)若DE+EF=10,求菱形ABCD的周长.
解:(1)证明:∵DE⊥AB,
∴∠AED=∠DEB=90°,
∵∠BAD=45°,∴∠ADE=∠BAD=45°,
∴AE=DE,
∵四边形ABCD是菱形,∴AC⊥BD,
∴∠OAB+∠ABD=∠BDE+∠ABD=90°,
∴∠OAB=∠BDE,
在△AEF和△DEB中,
∴△AEF≌△DEB(ASA).
(2)由(1)知,△AEF≌△DEB,∴EF=EB,
∴AB=AE+EB=DE+EF=10,
∵四边形ABCD是菱形,
∴菱形ABCD的周长为4AB=4×10=40.
