18.2.2.2 菱形的判定同步练习(含答案)
文档属性
| 名称 | 18.2.2.2 菱形的判定同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 17:28:13 | ||
图片预览


文档简介
18.1 平行四边形
18.2.2 菱形
第2课时 菱形的判定
一、选择题
1.下列选项中能使 ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
2.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
3.如图, ABCD的对角线AC,BD相交于点O,那么下列条件中,能判定 ABCD是菱形的为( )
A.AO=CO B.AO=BO C.∠AOB=90° D.∠BAD=∠ABC
第3题图 第4题图 第5题图
4.如图,在 ABCD中,对角线AC,BD相交于点O,下列条件能判定 ABCD为菱形的是( )
A.∠ABC=90° B.AC=BD C.AC⊥BD D.OA=OC,OB=OD
5.【2023深圳】如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形,则a的值为( )
A.1 B.2 C.3 D.4
6.如图,小红在作线段AB的垂直平分线时,操作如下:分别以点A,B为圆心,大于AB的长为半径,在线段AB的两侧画弧,分别相交于点C,D,则直线CD即为所求,连接AC,BC,AD,BD,根据她的作法可知四边形ADBC一定是( )
A.菱形 B.矩形 C.正方形 D.梯形
第6题图 第9题图 第10题图
7.已知平行四边形ABCD,下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.其中能使平行四边形ABCD是菱形的有( )
A.①③ B.②③ C.③④ D.①②③
8.在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.梯形
9.如图,两个长为9、宽为3的全等矩形叠合得到四边形ABCD,则四边形ABCD面积的最大值是( )
A.15 B.16 C.19 D.20
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形EFGH是菱形时,四边形ABCD的边至少满足条件( )
A.AB=AD B.AB=BC C.AB=CD D.BC=CD
二、填空题
11.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ABDC是菱形的依据是 .
第11题图 第13题图 第14题图
12.下列命题:
①四边都相等的四边形是菱形;
②两组邻边分别相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形;
④对角线相等的四边形是菱形;
⑤一条对角线平分一组对角的平行四边形是菱形.
其中正确的是 .(填序号)
13.如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (填序号).
14.如图,A(0,4),B(8,0),点C是x轴正半轴上一点,D是平面内任意一点,若以A,B,C,D为顶点的四边形是菱形,则点D的坐标为 .
三、解答题
15.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
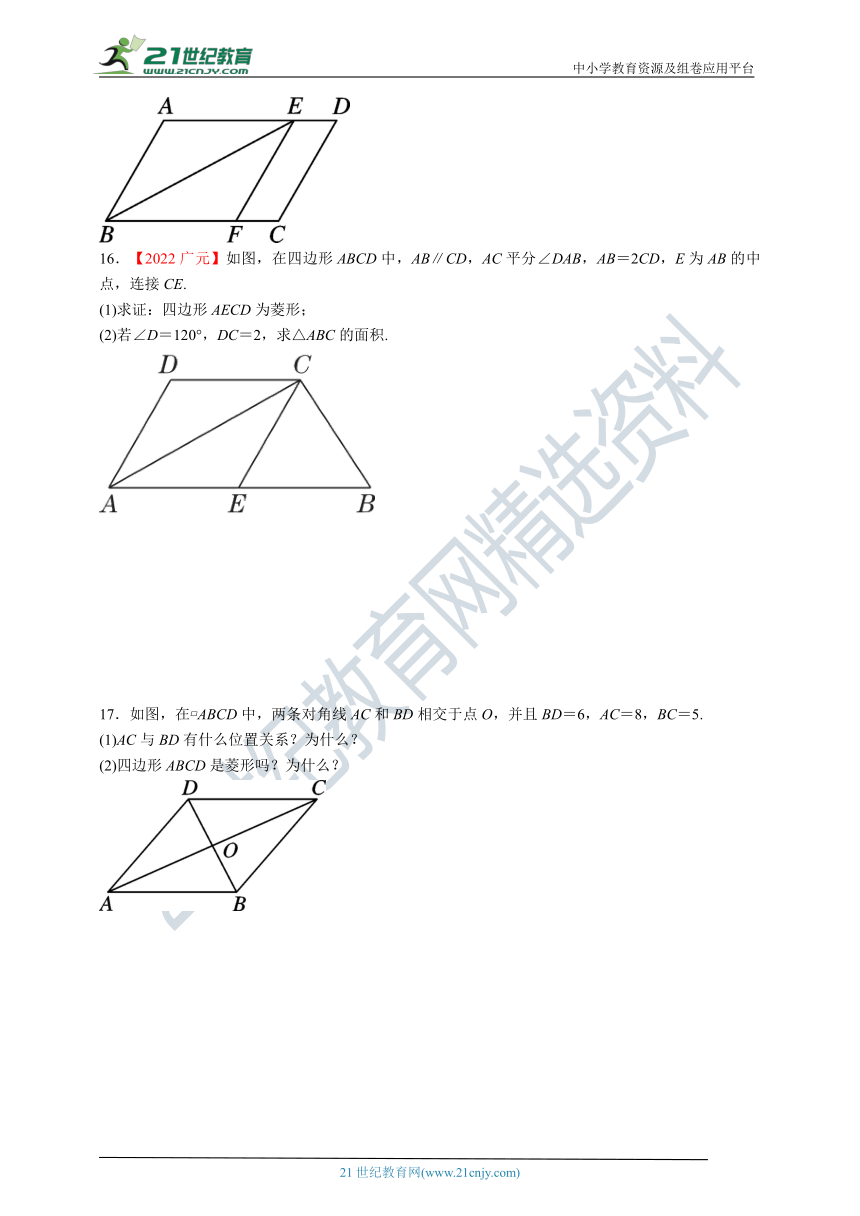
16.【2022广元】如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连接CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积.
17.如图,在 ABCD中,两条对角线AC和BD相交于点O,并且BD=6,AC=8,BC=5.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?
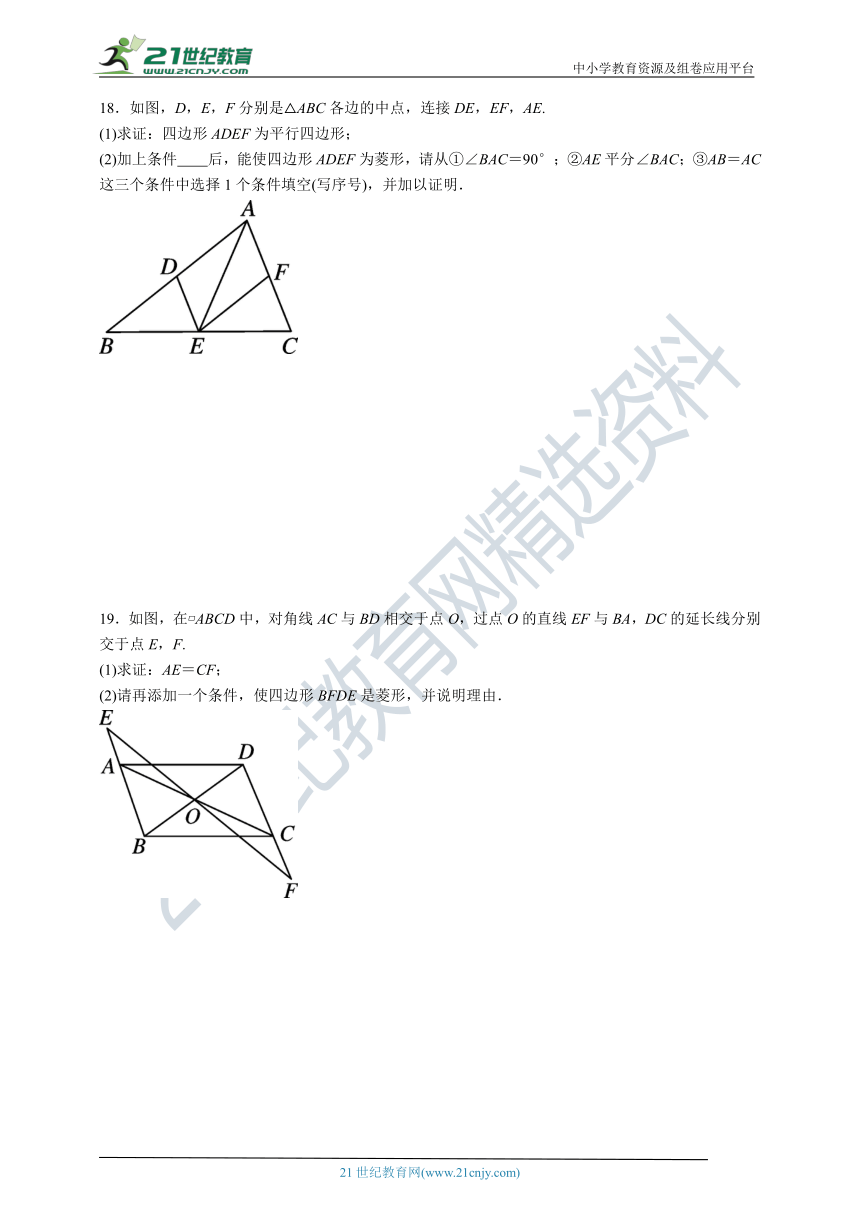
18.如图,D,E,F分别是△ABC各边的中点,连接DE,EF,AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
19.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
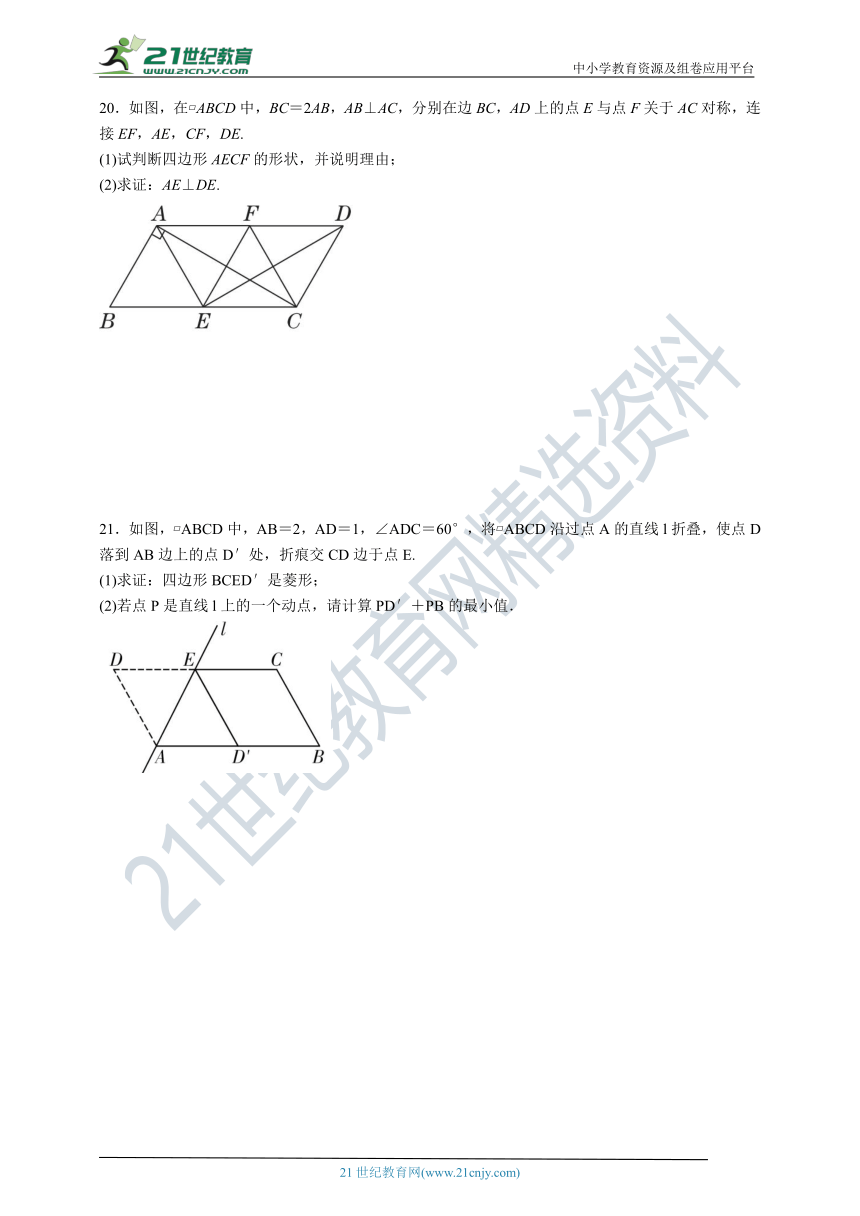
20.如图,在 ABCD中,BC=2AB,AB⊥AC,分别在边BC,AD上的点E与点F关于AC对称,连接EF,AE,CF,DE.
(1)试判断四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
21.如图, ABCD中,AB=2,AD=1,∠ADC=60°,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列选项中能使 ABCD成为菱形的是( B )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
2.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( A )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
3.如图, ABCD的对角线AC,BD相交于点O,那么下列条件中,能判定 ABCD是菱形的为( C )
A.AO=CO B.AO=BO C.∠AOB=90° D.∠BAD=∠ABC
第3题图 第4题图 第5题图
4.如图,在 ABCD中,对角线AC,BD相交于点O,下列条件能判定 ABCD为菱形的是( C )
A.∠ABC=90° B.AC=BD C.AC⊥BD D.OA=OC,OB=OD
5.【2023深圳】如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形,则a的值为( B )
A.1 B.2 C.3 D.4
6.如图,小红在作线段AB的垂直平分线时,操作如下:分别以点A,B为圆心,大于AB的长为半径,在线段AB的两侧画弧,分别相交于点C,D,则直线CD即为所求,连接AC,BC,AD,BD,根据她的作法可知四边形ADBC一定是( A )
A.菱形 B.矩形 C.正方形 D.梯形
第6题图 第9题图 第10题图
7.已知平行四边形ABCD,下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.其中能使平行四边形ABCD是菱形的有( A )
A.①③ B.②③ C.③④ D.①②③
8.在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( B )
A.矩形 B.菱形 C.正方形 D.梯形
9.如图,两个长为9、宽为3的全等矩形叠合得到四边形ABCD,则四边形ABCD面积的最大值是( A )
A.15 B.16 C.19 D.20
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形EFGH是菱形时,四边形ABCD的边至少满足条件( C )
A.AB=AD B.AB=BC C.AB=CD D.BC=CD
二、填空题
11.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ABDC是菱形的依据是 .
【答案】四条边相等的四边形是菱形
第11题图 第13题图 第14题图
12.下列命题:
①四边都相等的四边形是菱形;
②两组邻边分别相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形;
④对角线相等的四边形是菱形;
⑤一条对角线平分一组对角的平行四边形是菱形.
其中正确的是 .(填序号)
【答案】①③⑤
13.如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (填序号).
【答案】①
14.如图,A(0,4),B(8,0),点C是x轴正半轴上一点,D是平面内任意一点,若以A,B,C,D为顶点的四边形是菱形,则点D的坐标为 .
【答案】(5,4)或(4,4)
【解析】当AB为菱形的对角线时,如图①,设菱形的边长为m,∵A(0,4),B(8,0),∴OA=4,OB=8,∵四边形ACBD为菱形,∴CA=AD=BC,AD∥BC,∴CA=CB=m,OC=8-m,在Rt△AOC中,42+(8-m)2=m2,解得m=5,∴D(5,4);当AB为菱形的边时,如图②,AB==4,∵四边形ABCD为菱形,∴BC=AB=AD=4,AD∥BC,∴D(4,4).综上所述,D点坐标为(5,4)或(4,4).
图① 图②
三、解答题
15.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,
又∵EF∥AB,∴四边形ABFE是平行四边形,
∵BE平分∠ABC,∴∠ABE=∠FBE,
∵AD∥BC,∴∠AEB=∠EBF,
∴∠ABE=∠AEB,∴AB=AE,
∴平行四边形ABFE是菱形.
16.【2022广元】如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连接CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积.
(1)【证明】∵E为AB的中点,∴AB=2AE=2BE.
∵AB=2CD,∴CD=AE.
又∵AE∥CD,∴四边形AECD是平行四边形.
∵AC平分∠DAB,∴∠DAC=∠EAC.
∵AB∥CD,∴∠DCA=∠EAC.
∴∠DCA=∠DAC. ∴AD=CD.∴四边形AECD是菱形.
(2)【解】由四边形AECD是菱形,∠D=120°,DC=2,
可得△CEB是等边三角形.
∴BC=EC=2,∠B=60°.
∵∠CAE+∠ACE=∠CEB=60°,
∴∠CAE=∠ACE=30°.∴∠ACB=90°.
∵AB=2CD=4,∴AC=2.∴S△ABC=2.
17.如图,在 ABCD中,两条对角线AC和BD相交于点O,并且BD=6,AC=8,BC=5.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?
解:(1)AC⊥BD.
理由如下:∵四边形ABCD是平行四边形,
∴BO=DO=3,
AO=CO=4,
∵BC=5,∴BO2+CO2=CB2,
∴∠BOC=90°,
∴BD⊥AC.
(2)四边形ABCD是菱形.理由如下:
∵BD⊥AC,四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
18.如图,D,E,F分别是△ABC各边的中点,连接DE,EF,AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
解:(1)证明:∵D,E,F为AB,BC,AC的中点,
∴DE为△ABC的中位线,
∴DE∥AC,且DE=AC=AF.
即DE∥AF,DE=AF,
∴四边形ADEF为平行四边形.
(2)证明:选②,AE平分∠BAC.
∵AE平分∠BAC,∴∠DAE=∠FAE,
又∵ADEF为平行四边形,∴EF∥DA,
∴∠DAE=∠AEF,∴∠FAE=∠AEF,
∴AF=EF,
∴平行四边形ADEF为菱形.
选③,AB=AC.
∵EF∥AB且EF=AB,
DE∥AC且DE=AC,
又∵AB=AC,∴EF=DE,
∴平行四边形ADEF为菱形.
19.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,BE∥DF,∴∠E=∠F,
在△AOE和△COF中,
∴△AOE≌△COF(AAS),
∴AE=CF.
(2)当EF⊥BD时,四边形BFDE是菱形.理由如下:
如图,连接BF,DE,
∵四边形ABCD是平行四边形,
∴OB=OD,
∵△AOE≌△COF,∴OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,∴四边形BFDE是菱形.
20.如图,在 ABCD中,BC=2AB,AB⊥AC,分别在边BC,AD上的点E与点F关于AC对称,连接EF,AE,CF,DE.
(1)试判断四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
(1)【解】四边形AECF是菱形.理由如下:
设AC,EF交于点O,如图所示.
∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠OAF=∠OCE.
∵点E与点F关于AC对称,
∴AE=AF,CE=CF,OE=OF.
在△AOF和△COE中,
∴△AOF≌△COE(AAS).
∴AF=CE.
∴AE=AF=CE=CF.
∴四边形AECF是菱形.
(2)【证明】∵AB⊥AC,∴∠BAC=90°.
∴∠BAE+∠EAC=∠B+∠ACB=90°.由(1)知AE=EC,
∴∠EAC=∠ACB.∴∠BAE=∠B.∴AE=BE.∴BE=EC=BC.又∵BC=2AB,∴AB=BE=EC=AE.
∴△ABE是等边三角形.∴∠B=∠AEB=60°.
∴∠AEC=120°.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠DCE=180°-∠B=120°,CD=EC.
∴∠CED=∠CDE=(180°-120°)=30°.
∴∠AED=120°-30°=90°.∴AE⊥DE.
21.如图, ABCD中,AB=2,AD=1,∠ADC=60°,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
(1)证明:在 ABCD中,∵∠D=60°,
∴∠DAB=∠1+∠2=120°.
由题意知△ADE≌△AD′E,
∴∠1=∠2=∠D=60°,
∴△DEA和△AD′E是等边三角形,
∴DE=AD′=AD=ED′=1.
∵AB=2,∴D′B=1,同理EC=1,
∴EC=D′B=ED′=BC=1.
∴四边形BCED′是菱形.
(2)解:连接BD交AE于点P,连接PD′,BD的长即为所求,作DG⊥BA的延长线于点G.
∵∠DAB=120°,∴∠DAG=60°.
∵∠G=90°,∴∠ADG=30°.在Rt△ADG中,
∵AD=1,∴AG=,DG==.
∵AB=2,∴BG=.在Rt△BDG中,BD2=BG2+DG2=7,
∴BD=,即PD′+PB的最小值为.
18.2.2 菱形
第2课时 菱形的判定
一、选择题
1.下列选项中能使 ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
2.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
3.如图, ABCD的对角线AC,BD相交于点O,那么下列条件中,能判定 ABCD是菱形的为( )
A.AO=CO B.AO=BO C.∠AOB=90° D.∠BAD=∠ABC
第3题图 第4题图 第5题图
4.如图,在 ABCD中,对角线AC,BD相交于点O,下列条件能判定 ABCD为菱形的是( )
A.∠ABC=90° B.AC=BD C.AC⊥BD D.OA=OC,OB=OD
5.【2023深圳】如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形,则a的值为( )
A.1 B.2 C.3 D.4
6.如图,小红在作线段AB的垂直平分线时,操作如下:分别以点A,B为圆心,大于AB的长为半径,在线段AB的两侧画弧,分别相交于点C,D,则直线CD即为所求,连接AC,BC,AD,BD,根据她的作法可知四边形ADBC一定是( )
A.菱形 B.矩形 C.正方形 D.梯形
第6题图 第9题图 第10题图
7.已知平行四边形ABCD,下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.其中能使平行四边形ABCD是菱形的有( )
A.①③ B.②③ C.③④ D.①②③
8.在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.梯形
9.如图,两个长为9、宽为3的全等矩形叠合得到四边形ABCD,则四边形ABCD面积的最大值是( )
A.15 B.16 C.19 D.20
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形EFGH是菱形时,四边形ABCD的边至少满足条件( )
A.AB=AD B.AB=BC C.AB=CD D.BC=CD
二、填空题
11.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ABDC是菱形的依据是 .
第11题图 第13题图 第14题图
12.下列命题:
①四边都相等的四边形是菱形;
②两组邻边分别相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形;
④对角线相等的四边形是菱形;
⑤一条对角线平分一组对角的平行四边形是菱形.
其中正确的是 .(填序号)
13.如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (填序号).
14.如图,A(0,4),B(8,0),点C是x轴正半轴上一点,D是平面内任意一点,若以A,B,C,D为顶点的四边形是菱形,则点D的坐标为 .
三、解答题
15.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
16.【2022广元】如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连接CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积.
17.如图,在 ABCD中,两条对角线AC和BD相交于点O,并且BD=6,AC=8,BC=5.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?
18.如图,D,E,F分别是△ABC各边的中点,连接DE,EF,AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
19.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
20.如图,在 ABCD中,BC=2AB,AB⊥AC,分别在边BC,AD上的点E与点F关于AC对称,连接EF,AE,CF,DE.
(1)试判断四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
21.如图, ABCD中,AB=2,AD=1,∠ADC=60°,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列选项中能使 ABCD成为菱形的是( B )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
2.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( A )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
3.如图, ABCD的对角线AC,BD相交于点O,那么下列条件中,能判定 ABCD是菱形的为( C )
A.AO=CO B.AO=BO C.∠AOB=90° D.∠BAD=∠ABC
第3题图 第4题图 第5题图
4.如图,在 ABCD中,对角线AC,BD相交于点O,下列条件能判定 ABCD为菱形的是( C )
A.∠ABC=90° B.AC=BD C.AC⊥BD D.OA=OC,OB=OD
5.【2023深圳】如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形,则a的值为( B )
A.1 B.2 C.3 D.4
6.如图,小红在作线段AB的垂直平分线时,操作如下:分别以点A,B为圆心,大于AB的长为半径,在线段AB的两侧画弧,分别相交于点C,D,则直线CD即为所求,连接AC,BC,AD,BD,根据她的作法可知四边形ADBC一定是( A )
A.菱形 B.矩形 C.正方形 D.梯形
第6题图 第9题图 第10题图
7.已知平行四边形ABCD,下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.其中能使平行四边形ABCD是菱形的有( A )
A.①③ B.②③ C.③④ D.①②③
8.在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( B )
A.矩形 B.菱形 C.正方形 D.梯形
9.如图,两个长为9、宽为3的全等矩形叠合得到四边形ABCD,则四边形ABCD面积的最大值是( A )
A.15 B.16 C.19 D.20
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形EFGH是菱形时,四边形ABCD的边至少满足条件( C )
A.AB=AD B.AB=BC C.AB=CD D.BC=CD
二、填空题
11.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ABDC是菱形的依据是 .
【答案】四条边相等的四边形是菱形
第11题图 第13题图 第14题图
12.下列命题:
①四边都相等的四边形是菱形;
②两组邻边分别相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形;
④对角线相等的四边形是菱形;
⑤一条对角线平分一组对角的平行四边形是菱形.
其中正确的是 .(填序号)
【答案】①③⑤
13.如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (填序号).
【答案】①
14.如图,A(0,4),B(8,0),点C是x轴正半轴上一点,D是平面内任意一点,若以A,B,C,D为顶点的四边形是菱形,则点D的坐标为 .
【答案】(5,4)或(4,4)
【解析】当AB为菱形的对角线时,如图①,设菱形的边长为m,∵A(0,4),B(8,0),∴OA=4,OB=8,∵四边形ACBD为菱形,∴CA=AD=BC,AD∥BC,∴CA=CB=m,OC=8-m,在Rt△AOC中,42+(8-m)2=m2,解得m=5,∴D(5,4);当AB为菱形的边时,如图②,AB==4,∵四边形ABCD为菱形,∴BC=AB=AD=4,AD∥BC,∴D(4,4).综上所述,D点坐标为(5,4)或(4,4).
图① 图②
三、解答题
15.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,
又∵EF∥AB,∴四边形ABFE是平行四边形,
∵BE平分∠ABC,∴∠ABE=∠FBE,
∵AD∥BC,∴∠AEB=∠EBF,
∴∠ABE=∠AEB,∴AB=AE,
∴平行四边形ABFE是菱形.
16.【2022广元】如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连接CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积.
(1)【证明】∵E为AB的中点,∴AB=2AE=2BE.
∵AB=2CD,∴CD=AE.
又∵AE∥CD,∴四边形AECD是平行四边形.
∵AC平分∠DAB,∴∠DAC=∠EAC.
∵AB∥CD,∴∠DCA=∠EAC.
∴∠DCA=∠DAC. ∴AD=CD.∴四边形AECD是菱形.
(2)【解】由四边形AECD是菱形,∠D=120°,DC=2,
可得△CEB是等边三角形.
∴BC=EC=2,∠B=60°.
∵∠CAE+∠ACE=∠CEB=60°,
∴∠CAE=∠ACE=30°.∴∠ACB=90°.
∵AB=2CD=4,∴AC=2.∴S△ABC=2.
17.如图,在 ABCD中,两条对角线AC和BD相交于点O,并且BD=6,AC=8,BC=5.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?
解:(1)AC⊥BD.
理由如下:∵四边形ABCD是平行四边形,
∴BO=DO=3,
AO=CO=4,
∵BC=5,∴BO2+CO2=CB2,
∴∠BOC=90°,
∴BD⊥AC.
(2)四边形ABCD是菱形.理由如下:
∵BD⊥AC,四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
18.如图,D,E,F分别是△ABC各边的中点,连接DE,EF,AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
解:(1)证明:∵D,E,F为AB,BC,AC的中点,
∴DE为△ABC的中位线,
∴DE∥AC,且DE=AC=AF.
即DE∥AF,DE=AF,
∴四边形ADEF为平行四边形.
(2)证明:选②,AE平分∠BAC.
∵AE平分∠BAC,∴∠DAE=∠FAE,
又∵ADEF为平行四边形,∴EF∥DA,
∴∠DAE=∠AEF,∴∠FAE=∠AEF,
∴AF=EF,
∴平行四边形ADEF为菱形.
选③,AB=AC.
∵EF∥AB且EF=AB,
DE∥AC且DE=AC,
又∵AB=AC,∴EF=DE,
∴平行四边形ADEF为菱形.
19.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,BE∥DF,∴∠E=∠F,
在△AOE和△COF中,
∴△AOE≌△COF(AAS),
∴AE=CF.
(2)当EF⊥BD时,四边形BFDE是菱形.理由如下:
如图,连接BF,DE,
∵四边形ABCD是平行四边形,
∴OB=OD,
∵△AOE≌△COF,∴OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,∴四边形BFDE是菱形.
20.如图,在 ABCD中,BC=2AB,AB⊥AC,分别在边BC,AD上的点E与点F关于AC对称,连接EF,AE,CF,DE.
(1)试判断四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
(1)【解】四边形AECF是菱形.理由如下:
设AC,EF交于点O,如图所示.
∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠OAF=∠OCE.
∵点E与点F关于AC对称,
∴AE=AF,CE=CF,OE=OF.
在△AOF和△COE中,
∴△AOF≌△COE(AAS).
∴AF=CE.
∴AE=AF=CE=CF.
∴四边形AECF是菱形.
(2)【证明】∵AB⊥AC,∴∠BAC=90°.
∴∠BAE+∠EAC=∠B+∠ACB=90°.由(1)知AE=EC,
∴∠EAC=∠ACB.∴∠BAE=∠B.∴AE=BE.∴BE=EC=BC.又∵BC=2AB,∴AB=BE=EC=AE.
∴△ABE是等边三角形.∴∠B=∠AEB=60°.
∴∠AEC=120°.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠DCE=180°-∠B=120°,CD=EC.
∴∠CED=∠CDE=(180°-120°)=30°.
∴∠AED=120°-30°=90°.∴AE⊥DE.
21.如图, ABCD中,AB=2,AD=1,∠ADC=60°,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
(1)证明:在 ABCD中,∵∠D=60°,
∴∠DAB=∠1+∠2=120°.
由题意知△ADE≌△AD′E,
∴∠1=∠2=∠D=60°,
∴△DEA和△AD′E是等边三角形,
∴DE=AD′=AD=ED′=1.
∵AB=2,∴D′B=1,同理EC=1,
∴EC=D′B=ED′=BC=1.
∴四边形BCED′是菱形.
(2)解:连接BD交AE于点P,连接PD′,BD的长即为所求,作DG⊥BA的延长线于点G.
∵∠DAB=120°,∴∠DAG=60°.
∵∠G=90°,∴∠ADG=30°.在Rt△ADG中,
∵AD=1,∴AG=,DG==.
∵AB=2,∴BG=.在Rt△BDG中,BD2=BG2+DG2=7,
∴BD=,即PD′+PB的最小值为.
