2024辽宁中考数学二轮专题复习 微专题 遇到角平分线如何添加辅助线 课件(共26张PPT)
文档属性
| 名称 | 2024辽宁中考数学二轮专题复习 微专题 遇到角平分线如何添加辅助线 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 13:54:37 | ||
图片预览


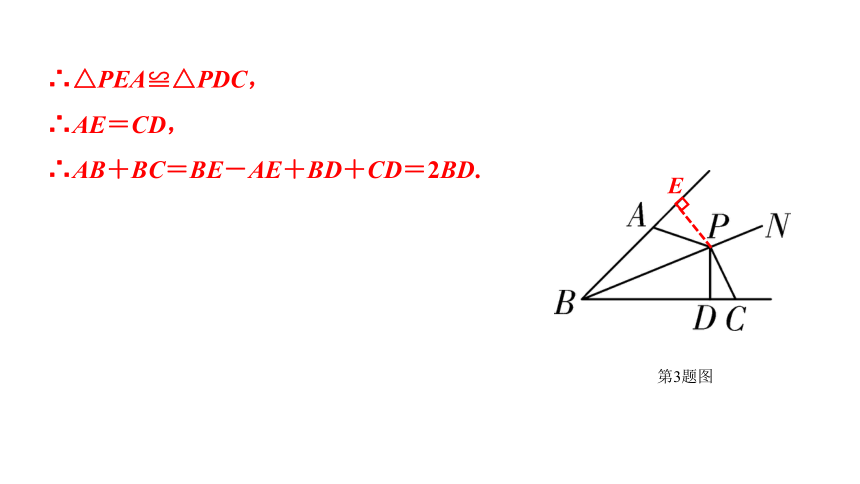


文档简介
(共26张PPT)
微专题 遇到角平分线如何添加辅助线
方法一 过角平分线上一点向角两边作垂线
方法解读
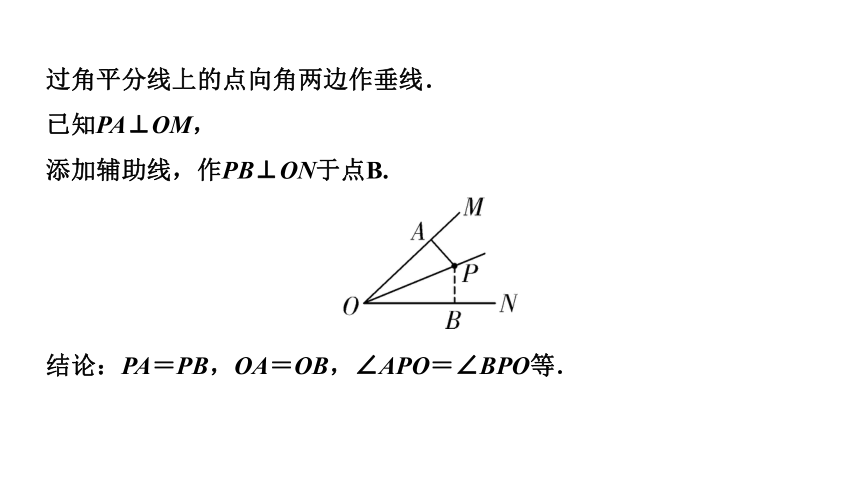
如图,已知∠MON,点P是∠MON平分线上一点.
过角平分线上的点向角两边作垂线.
已知PA⊥OM,
添加辅助线,作PB⊥ON于点B.
结论:PA=PB,OA=OB,∠APO=∠BPO等.
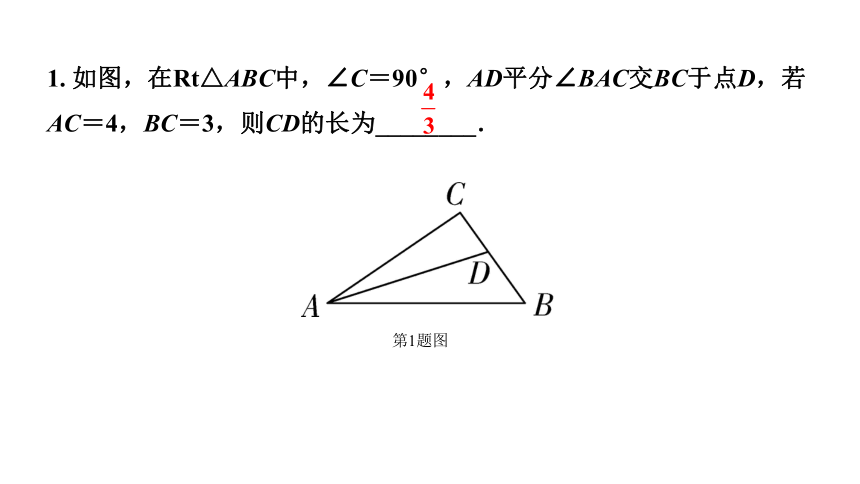
1. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AC=4,BC=3,则CD的长为________.
第1题图
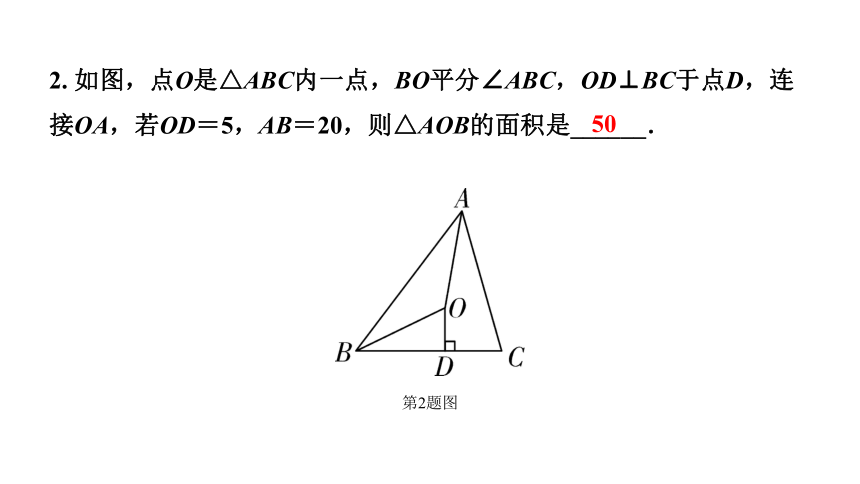
2. 如图,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=5,AB=20,则△AOB的面积是______.
第2题图
50
3. 如图,∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.
第3题图
证明:如解图,过点P作PE⊥BA于点E,
E
∴∠PEA=∠PDC=90°,
又∵∠BAP+∠BCP=180°,
∴∠PAE=∠PCD.
又∵∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,
∴BE=BD,PE=PD,
∴△PEA≌△PDC,
∴AE=CD,
∴AB+BC=BE-AE+BD+CD=2BD.
第3题图
E
方法二 角平分线遇平行线,构造等腰三角形
方法解读
角平分线+平行线=等腰三角形
1.过点P作PQ∥ON.
2.若∠MON 为钝角,过点P作PQ∥ON.
结论:△OPQ为等腰三角形.
知二推三:①点P为∠AOB(或其外角)平分线上一点;②PQ∥OB;③△POQ为等腰三角形.知道其中任意两个条件,均可推出第三条结论.
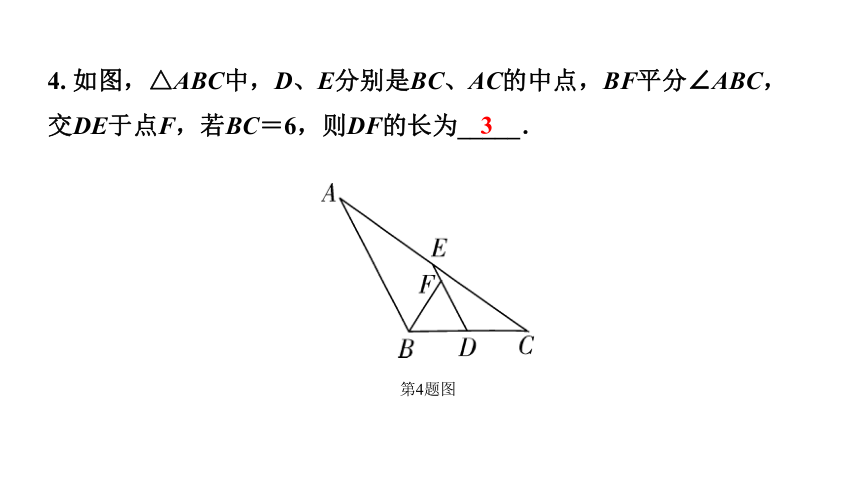
4. 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长为_____.
第4题图
3
5. 如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于点E,连接CE并延长交AP于点D.求证:AB=AD+BC.
第5题图
证明:如解图,延长AE交BC的延长线于点M,
M
∵AE平分∠PAB,BE平分∠CBA,
∴∠1=∠2,∠3=∠4,
∵AD∥BC,
∴∠1=∠M=∠2,∠1+∠2+∠3+∠4=180°,
∴BM=BA,∠3+∠2=90°,
∴BE⊥AM,
在△ABE和△MBE中,
∴△ABE≌△MBE,∴AE=ME,
在△ADE和△MCE中,
∴△ADE≌△MCE,∴AD=CM,
∴AB=BM=BC+CM=BC+AD
第5题图
M
方法三 利用角平分线,构造对称图形
方法解读
图中有角平分线,可将图形对折看,对折以后关系现.
已知A为OM上任意一点,O为∠MON平分线上一点,连接AP.在ON上截取OB=OA,连接PB.
结论:________________________________
△AOP≌△BOP,AP=BP
6. 如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,若AC=16,AD=8,则线段BC的长为______.
第6题图
24
7. 如图,四边形ABCD中,AC平分∠BAD,∠B+∠ADC=180°,若BC=2,则DC的长为_____.
第7题图
2
方法四 作角平分线的垂线,构造等腰三角形
方法解读
过角平分线上的点作角平分线的垂线,三线合一试试看.
已知AP⊥OP,延长AP交ON于点B.
结论:_________________________________________
Rt△AOP≌Rt△BOP,OA=OB,AP=BP.
8. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD.若BD=1,BC=3,则AC的长为_____.
第8题图
5
9. 如图,在平行四边形ABCD中,BD为对角线,∠BAD的平分线交BC于点E,过点B作BF⊥AE于点F,连接DF.已知S△ADF=14,S△ABF=10,则平行四边形ABCD的面积为______.
第9题图
56
综合训练
1. 如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A. 2 B. 2.5 C. 3 D. 4
第1题图
A
2. 如图,AB∥CD,∠ABC的平分线与∠BCD的平分线相交于点E,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,则PE的最小值为______.
第2题图
4
3. 如图,∠MON=30°,OP平分∠MON,过点P作PQ∥OM交ON于点Q.若OQ=4,则点P到OM的距离为_____.
第3题图
2
4. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,BF是∠CBA的平分线,过点A作AD⊥BF,交BF延长线于点D,若AD=6,则BF的长为______.
第4题图
12
5. 如图,OC是∠AOB的平分线,P是OC上的一点,过点P作PD⊥OA,PE⊥OB,垂足分别为点D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
第5题图
证明:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE,
在Rt△OPD和Rt△OPE中,
∴Rt△OPD≌Rt△OPE(HL),
∴OD=OE,
∵OC是∠AOB的平分线,
∴∠DOF=∠EOF,
在△ODF和△OEF中,
∴△ODF≌△OEF(SAS),
∴DF=EF.
第5题图
6. 如图,在△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,延长BD至点E,连接EC,DE=AD,试求∠ECA的度数.
第6题图
解:如解图,在BC上截取BF=AB,连接DF,
F
∵BD是∠ABC的平分线,
∴∠ABD=∠FBD,
在△ABD和△FBD中,
∴△ABD≌△FBD(SAS),∴∠BFD=∠A,AD=DF,
∵AD=DE,
∴DE=DF,
∴∠DFC=180°-∠A=80°,
又∵∠ABC=∠ACB=40°,
∴∠FDC=60°,
∵∠EDC=∠ADB=180°-∠ABD-∠A=60°,
∴∠EDC=∠FDC,
第6题图
F
在△DCE和△DCF中,
∴△DCE≌△DCF(SAS),
∴∠ECA=∠DCB=40°.
第6题图
F
微专题 遇到角平分线如何添加辅助线
方法一 过角平分线上一点向角两边作垂线
方法解读
如图,已知∠MON,点P是∠MON平分线上一点.
过角平分线上的点向角两边作垂线.
已知PA⊥OM,
添加辅助线,作PB⊥ON于点B.
结论:PA=PB,OA=OB,∠APO=∠BPO等.
1. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AC=4,BC=3,则CD的长为________.
第1题图
2. 如图,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=5,AB=20,则△AOB的面积是______.
第2题图
50
3. 如图,∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.
第3题图
证明:如解图,过点P作PE⊥BA于点E,
E
∴∠PEA=∠PDC=90°,
又∵∠BAP+∠BCP=180°,
∴∠PAE=∠PCD.
又∵∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,
∴BE=BD,PE=PD,
∴△PEA≌△PDC,
∴AE=CD,
∴AB+BC=BE-AE+BD+CD=2BD.
第3题图
E
方法二 角平分线遇平行线,构造等腰三角形
方法解读
角平分线+平行线=等腰三角形
1.过点P作PQ∥ON.
2.若∠MON 为钝角,过点P作PQ∥ON.
结论:△OPQ为等腰三角形.
知二推三:①点P为∠AOB(或其外角)平分线上一点;②PQ∥OB;③△POQ为等腰三角形.知道其中任意两个条件,均可推出第三条结论.
4. 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长为_____.
第4题图
3
5. 如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于点E,连接CE并延长交AP于点D.求证:AB=AD+BC.
第5题图
证明:如解图,延长AE交BC的延长线于点M,
M
∵AE平分∠PAB,BE平分∠CBA,
∴∠1=∠2,∠3=∠4,
∵AD∥BC,
∴∠1=∠M=∠2,∠1+∠2+∠3+∠4=180°,
∴BM=BA,∠3+∠2=90°,
∴BE⊥AM,
在△ABE和△MBE中,
∴△ABE≌△MBE,∴AE=ME,
在△ADE和△MCE中,
∴△ADE≌△MCE,∴AD=CM,
∴AB=BM=BC+CM=BC+AD
第5题图
M
方法三 利用角平分线,构造对称图形
方法解读
图中有角平分线,可将图形对折看,对折以后关系现.
已知A为OM上任意一点,O为∠MON平分线上一点,连接AP.在ON上截取OB=OA,连接PB.
结论:________________________________
△AOP≌△BOP,AP=BP
6. 如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,若AC=16,AD=8,则线段BC的长为______.
第6题图
24
7. 如图,四边形ABCD中,AC平分∠BAD,∠B+∠ADC=180°,若BC=2,则DC的长为_____.
第7题图
2
方法四 作角平分线的垂线,构造等腰三角形
方法解读
过角平分线上的点作角平分线的垂线,三线合一试试看.
已知AP⊥OP,延长AP交ON于点B.
结论:_________________________________________
Rt△AOP≌Rt△BOP,OA=OB,AP=BP.
8. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD.若BD=1,BC=3,则AC的长为_____.
第8题图
5
9. 如图,在平行四边形ABCD中,BD为对角线,∠BAD的平分线交BC于点E,过点B作BF⊥AE于点F,连接DF.已知S△ADF=14,S△ABF=10,则平行四边形ABCD的面积为______.
第9题图
56
综合训练
1. 如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A. 2 B. 2.5 C. 3 D. 4
第1题图
A
2. 如图,AB∥CD,∠ABC的平分线与∠BCD的平分线相交于点E,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,则PE的最小值为______.
第2题图
4
3. 如图,∠MON=30°,OP平分∠MON,过点P作PQ∥OM交ON于点Q.若OQ=4,则点P到OM的距离为_____.
第3题图
2
4. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,BF是∠CBA的平分线,过点A作AD⊥BF,交BF延长线于点D,若AD=6,则BF的长为______.
第4题图
12
5. 如图,OC是∠AOB的平分线,P是OC上的一点,过点P作PD⊥OA,PE⊥OB,垂足分别为点D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
第5题图
证明:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE,
在Rt△OPD和Rt△OPE中,
∴Rt△OPD≌Rt△OPE(HL),
∴OD=OE,
∵OC是∠AOB的平分线,
∴∠DOF=∠EOF,
在△ODF和△OEF中,
∴△ODF≌△OEF(SAS),
∴DF=EF.
第5题图
6. 如图,在△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,延长BD至点E,连接EC,DE=AD,试求∠ECA的度数.
第6题图
解:如解图,在BC上截取BF=AB,连接DF,
F
∵BD是∠ABC的平分线,
∴∠ABD=∠FBD,
在△ABD和△FBD中,
∴△ABD≌△FBD(SAS),∴∠BFD=∠A,AD=DF,
∵AD=DE,
∴DE=DF,
∴∠DFC=180°-∠A=80°,
又∵∠ABC=∠ACB=40°,
∴∠FDC=60°,
∵∠EDC=∠ADB=180°-∠ABD-∠A=60°,
∴∠EDC=∠FDC,
第6题图
F
在△DCE和△DCF中,
∴△DCE≌△DCF(SAS),
∴∠ECA=∠DCB=40°.
第6题图
F
同课章节目录
