2024辽宁中考数学二轮专题复习 微专题 常考相似模型 课件(共35张PPT)
文档属性
| 名称 | 2024辽宁中考数学二轮专题复习 微专题 常考相似模型 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 365.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 13:54:11 | ||
图片预览





文档简介
(共35张PPT)
微专题 常考相似模型
模型分析
模型一 A字型
模型展示 正A字型 斜A字型
模型特点 有一个公共角∠A 模型分析 DE∥BC, 则∠ADE=∠B,∠AED=∠C ∠ADE=∠ACB,
∠AED=∠B
结论 △ADE∽△ABC △ADE∽△ACB
模型应用
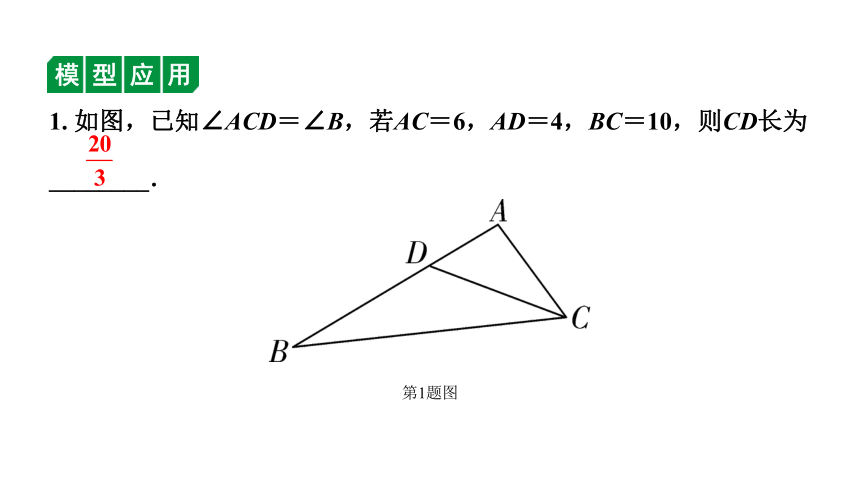
第1题图
1. 如图,已知∠ACD=∠B,若AC=6,AD=4,BC=10,则CD长为
________.
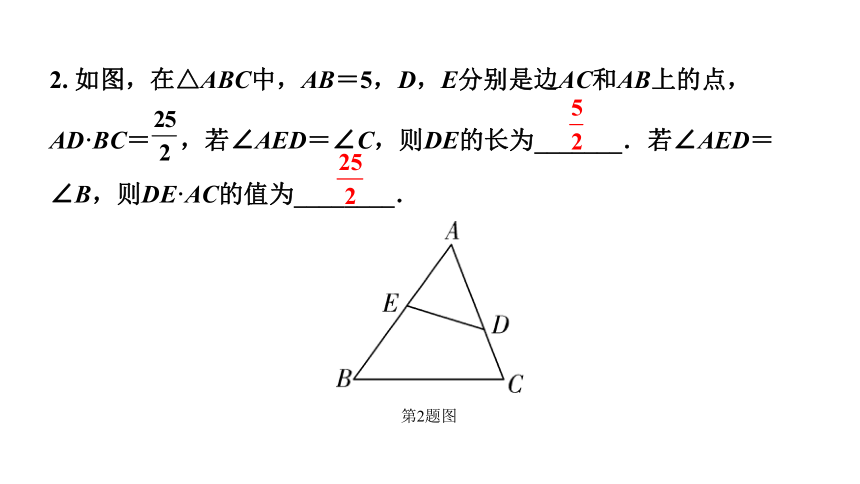
2. 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,
AD·BC= ,若∠AED=∠C,则DE的长为_______.若∠AED=
∠B,则DE·AC的值为________.
第2题图
模型二 8字型
模型分析
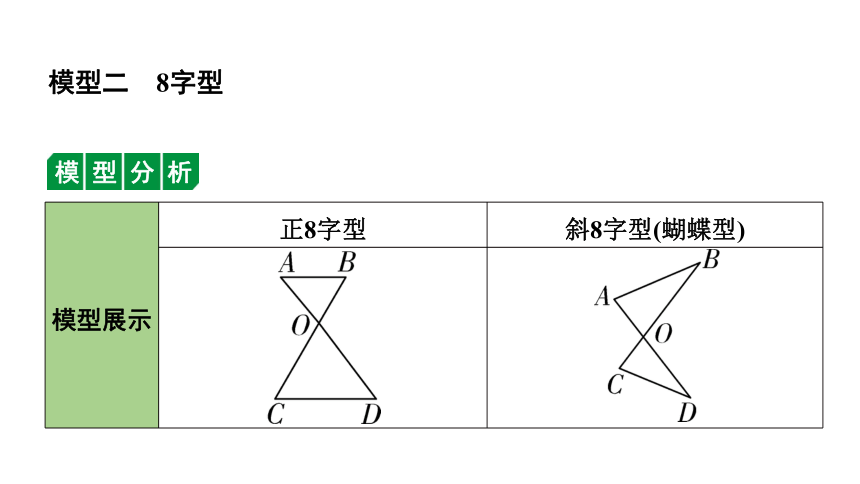
模型展示 正8字型 斜8字型(蝴蝶型)
模型特点 有一组对顶角 模型分析 AB∥CD, 则∠A=∠D,∠B=∠C ∠A=∠C,∠B=∠D
结论 △AOB∽△DOC △AOB∽△COD
模型应用
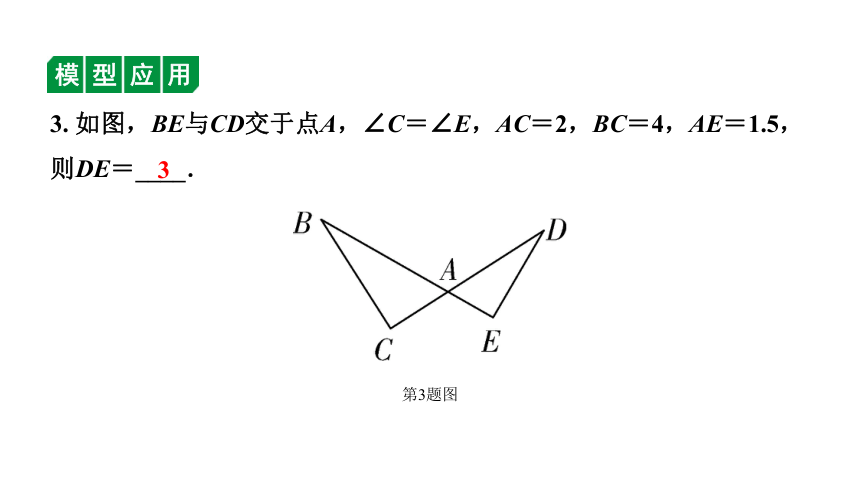
3. 如图,BE与CD交于点A,∠C=∠E,AC=2,BC=4,AE=1.5,则DE=____.
第3题图
3
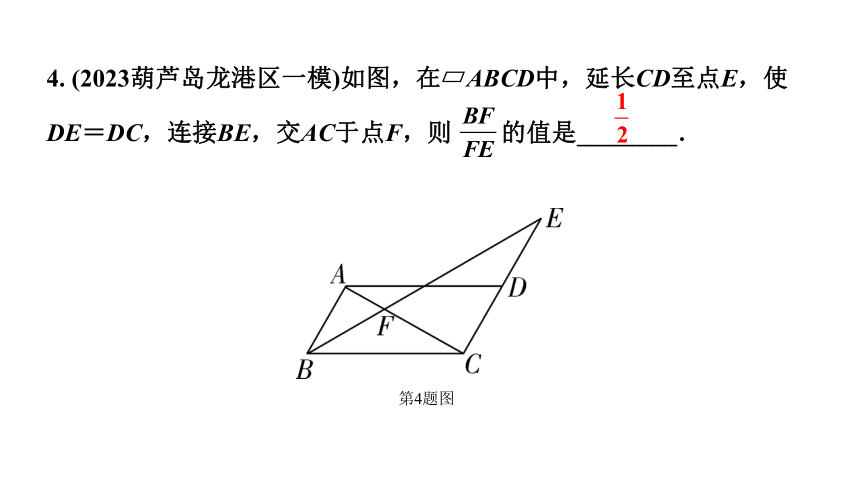
4. (2023葫芦岛龙港区一模)如图,在 ABCD中,延长CD至点E,使
DE=DC,连接BE,交AC于点F,则 的值是________.
第4题图
5. 如图,△ABC是等腰直角三角形,∠C=90°,D为边BC上一点,连接AD,过点B作BE⊥AD,交AD的延长线于点E.若 ,则
的值为________.
第5题图
模型分析
模型三 三垂直型
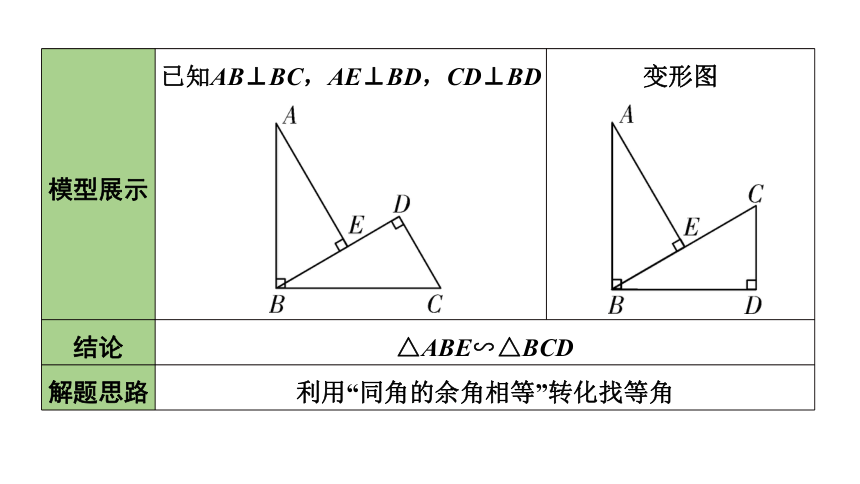
模型展示 已知AB⊥BC,DE⊥CE,AC⊥CD 变形图
结论:△ABC∽△CED 模型展示 已知AB⊥BC,AE⊥BD,CD⊥BD 变形图
结论 △ABE∽△BCD 解题思路 利用“同角的余角相等”转化找等角 模型应用
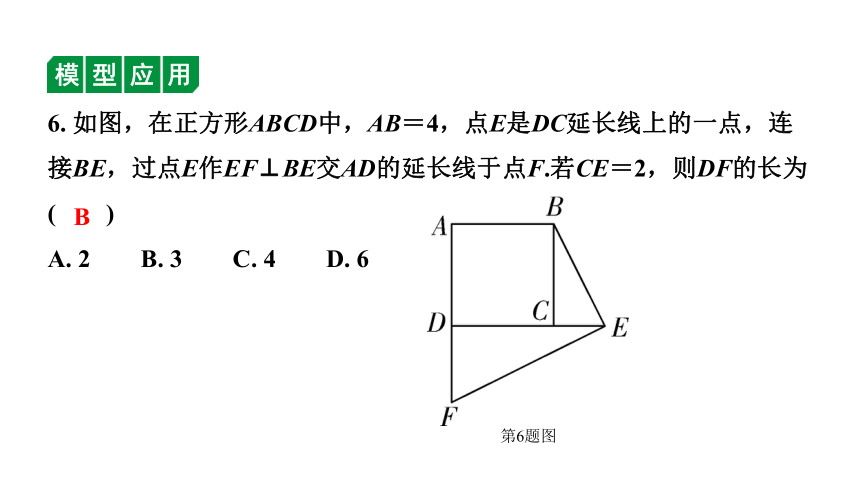
6. 如图,在正方形ABCD中,AB=4,点E是DC延长线上的一点,连接BE,过点E作EF⊥BE交AD的延长线于点F.若CE=2,则DF的长为( )
A. 2 B. 3 C. 4 D. 6
第6题图
B
模型四 手拉手型
模型分析
模型展示
模型特点 等顶角(∠DAE=∠BAC),非等线段(AD≠AE,AB≠AC),共顶点
模型分析 ∠BAD=∠CAE,∠ADE=∠ABC
解题思路 证明三角形相似的关键
(1)共顶点:加(减)共顶点的公共角得到∠BAD=∠CAE
(2)利用 证明相等角的两边成比例
结论 △ADE∽△ABC,△ABD∽△ACE
拓展 当线段AD=AE,AB=AC时,△ABD≌△ACE
模型应用
第7题图
7. 如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,若AC∶BC=3∶4,则BD∶CE为( )
A. 5∶3 B. 4∶3 C. ∶2 D. 2∶
A
模型五 对角互补型
模型分析
模型展示 (OE≠OF)
(OA≠OM)∠ACB+∠EOF=180°
模型特点 对角互补 模型分析 过点O作OD⊥AC,OH⊥BC,则∠EDO=∠FHO 作∠MOF=∠AOE
结论 △ODE∽△OHF △OAE∽△OMF
拓展 当OE=OF时,△ODE≌△OHF 当OE=OF时,△OAE≌△OMF
模型应用
8. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,在Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=______.
第8题图
6
9. 如图,已知△ABC是等边三角形,点D,E,F分别是AB,AC,BC边上的点,∠EDF=120°,设 =n.若 ,求n的值.
第9题图
解:如解图,作DG∥BC交AC于点G,
G
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵DG∥BC,
∴∠B=∠ADG=∠C=∠AGD=60°,∠BDG=120°,
∴△ADG是等边三角形,∴AD=DG,
∵∠BGD=120°,∠EDF=120°,
∴∠BDF+∠GDF=∠EDG+∠GDF=120°,
∴∠BDF=∠GDE,
∵∠B=∠AGD=60°,
∴△DGE∽△DBF,
∴ ,
∴ ,
第9题图
G
∵ ,
∴n+ =3,化简得,n2-3n+1=0,
解得n1= ,n2= ,
∴n的值为 或 .
第9题图
G
综合训练
第1题图
1. 如图,点O为平行四边形ABCD的对角线AC和BD的交点,点E为边
BC的中点,连接AE交BD于点F,则 的值为________.
第2题图
2. 如图,△ABC为锐角三角形,AD是BC边上的高,矩形PQMN的顶点P,N分别在AB,AC上,Q、M在BC上,若BC=12,AD=8,QM
=x,矩形PQMN的面积是__________.(用含x的代数式表示)
第3题图
3. 如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,E为AB上一点,ED,BC的延长线交于点F,∠F=30°,ED=2,DF=6,BE= ,则BC的长为_______.
第4题图
4. 如图,矩形ABCD中,AB=4,AD=6,点E是边CD上一点,
EF⊥AE交BC于点F,则CF长的取值范围是____________.
第5题图
5. 如图,在△ABC中,AB=2,AC= ,D为△ABC内部的一点,且CD⊥BD,在BD的延长线上取一点E,使得∠CAE=∠BAD.若∠ADE
=∠ABC,且∠DBC=30°,则AD的长为________.
第6题图
6. 如图,在Rt△ABC中,∠C=90°,AC=BC,AP、BP分别平分∠CAB、∠CBA,过点P作DE∥AB交AC于点D,交BC于点E.
(1)求证:点P是线段DE的中点;
证明:(1)∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵DE∥AB,
∴∠ABP=∠EPB,∴∠CBP=∠EPB,
∴BE=PE,
同理可证DP=DA,
∵DE∥AB,
∴ ,
∵CA=CB,
∴CE=CD,
∴BE=AD,
∴PE=PD,
∴点P是DE的中点;
第6题图
(2)求证:BP2=BE·BA.
(2)由(1)得∠ABP=∠EBP=∠EPB= ∠CBA,
∵AP平分∠CAB,
∴∠PAB= ∠CAB,
∵CA=CB,
∴∠CBA=∠CAB,
∴∠ABP=∠EBP=∠EPB=∠PAB,
∴△ABP∽△PBE,
∴ ,∴BP2=BA·BE.
第6题图
第7题图①
7. 已知△ABC和△DCE中,AB=AC,DC=DE,BF=EF,点B,C,E都在同一直线上,且△ABC和△DCE在该直线同侧.
(1)如图①,若∠BAC=∠CDE=90°,请猜想线段AF与DF之间的数量关系和位置关系,并证明你的猜想;
解:(1)猜想:AF=DF,AF⊥DF.
证明:如解图,过点A作AH⊥BC于点H,过点D作DJ⊥EC于点J.
H
J
∵AB=AC,DC=DE,∠BAC=∠CDE=90°,
∴BH=CH,CJ=EJ,
∴AH=BH=CH,DJ=CJ=EJ,
∵BF=EF,
∴HJ=BF=EF,
∴BH=FJ=AH,FH=JE=DJ,
∵∠AHF=∠FJD=90°,
∴△AHF≌△FJD(SAS),
∴AF=FD,∠HAF=∠JFD,
第7题图①
H
J
∵∠FAH+∠AFH=90°,
∴∠AFH+∠DFJ=90°,
∴∠AFD=90°,即AF⊥DF;
第7题图①
H
J
(2)如图②,若∠BAC=60°,∠CDE=120°,请直接写出线段AF与DF之间的数量关系和位置关系.
第7题图②
【解法提示】如解图②,过点A作AH⊥BC于点H,过点D作DJ⊥EC于点J.
H
J
∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴BH=CH,AH= BH,
∵DC=DE,∠CDE=120°,
∴CJ=JE,∠DEC=∠DCE=30°,∴JE= DJ,
∵BF=FE,
∴HJ=BF=EF,∴BH=FJ,HF=JE,
∴AH= FJ,FH= DJ,∴ ,
∵∠AHF=∠FJD=90°,
∴△AHF∽△FJD,
∴ ,∠HAF=∠DFJ,
第7题图②
H
J
∵∠FAH+∠AFH=90°,
∴∠AFH+∠DFJ=90°,
∴∠AFD=90°,即AF⊥DF,
∴AF= DF,AF⊥DF.
(2)AF= DF,AF⊥DF.
第7题图②
H
J
微专题 常考相似模型
模型分析
模型一 A字型
模型展示 正A字型 斜A字型
模型特点 有一个公共角∠A 模型分析 DE∥BC, 则∠ADE=∠B,∠AED=∠C ∠ADE=∠ACB,
∠AED=∠B
结论 △ADE∽△ABC △ADE∽△ACB
模型应用
第1题图
1. 如图,已知∠ACD=∠B,若AC=6,AD=4,BC=10,则CD长为
________.
2. 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,
AD·BC= ,若∠AED=∠C,则DE的长为_______.若∠AED=
∠B,则DE·AC的值为________.
第2题图
模型二 8字型
模型分析
模型展示 正8字型 斜8字型(蝴蝶型)
模型特点 有一组对顶角 模型分析 AB∥CD, 则∠A=∠D,∠B=∠C ∠A=∠C,∠B=∠D
结论 △AOB∽△DOC △AOB∽△COD
模型应用
3. 如图,BE与CD交于点A,∠C=∠E,AC=2,BC=4,AE=1.5,则DE=____.
第3题图
3
4. (2023葫芦岛龙港区一模)如图,在 ABCD中,延长CD至点E,使
DE=DC,连接BE,交AC于点F,则 的值是________.
第4题图
5. 如图,△ABC是等腰直角三角形,∠C=90°,D为边BC上一点,连接AD,过点B作BE⊥AD,交AD的延长线于点E.若 ,则
的值为________.
第5题图
模型分析
模型三 三垂直型
模型展示 已知AB⊥BC,DE⊥CE,AC⊥CD 变形图
结论:△ABC∽△CED 模型展示 已知AB⊥BC,AE⊥BD,CD⊥BD 变形图
结论 △ABE∽△BCD 解题思路 利用“同角的余角相等”转化找等角 模型应用
6. 如图,在正方形ABCD中,AB=4,点E是DC延长线上的一点,连接BE,过点E作EF⊥BE交AD的延长线于点F.若CE=2,则DF的长为( )
A. 2 B. 3 C. 4 D. 6
第6题图
B
模型四 手拉手型
模型分析
模型展示
模型特点 等顶角(∠DAE=∠BAC),非等线段(AD≠AE,AB≠AC),共顶点
模型分析 ∠BAD=∠CAE,∠ADE=∠ABC
解题思路 证明三角形相似的关键
(1)共顶点:加(减)共顶点的公共角得到∠BAD=∠CAE
(2)利用 证明相等角的两边成比例
结论 △ADE∽△ABC,△ABD∽△ACE
拓展 当线段AD=AE,AB=AC时,△ABD≌△ACE
模型应用
第7题图
7. 如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,若AC∶BC=3∶4,则BD∶CE为( )
A. 5∶3 B. 4∶3 C. ∶2 D. 2∶
A
模型五 对角互补型
模型分析
模型展示 (OE≠OF)
(OA≠OM)∠ACB+∠EOF=180°
模型特点 对角互补 模型分析 过点O作OD⊥AC,OH⊥BC,则∠EDO=∠FHO 作∠MOF=∠AOE
结论 △ODE∽△OHF △OAE∽△OMF
拓展 当OE=OF时,△ODE≌△OHF 当OE=OF时,△OAE≌△OMF
模型应用
8. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,在Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=______.
第8题图
6
9. 如图,已知△ABC是等边三角形,点D,E,F分别是AB,AC,BC边上的点,∠EDF=120°,设 =n.若 ,求n的值.
第9题图
解:如解图,作DG∥BC交AC于点G,
G
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵DG∥BC,
∴∠B=∠ADG=∠C=∠AGD=60°,∠BDG=120°,
∴△ADG是等边三角形,∴AD=DG,
∵∠BGD=120°,∠EDF=120°,
∴∠BDF+∠GDF=∠EDG+∠GDF=120°,
∴∠BDF=∠GDE,
∵∠B=∠AGD=60°,
∴△DGE∽△DBF,
∴ ,
∴ ,
第9题图
G
∵ ,
∴n+ =3,化简得,n2-3n+1=0,
解得n1= ,n2= ,
∴n的值为 或 .
第9题图
G
综合训练
第1题图
1. 如图,点O为平行四边形ABCD的对角线AC和BD的交点,点E为边
BC的中点,连接AE交BD于点F,则 的值为________.
第2题图
2. 如图,△ABC为锐角三角形,AD是BC边上的高,矩形PQMN的顶点P,N分别在AB,AC上,Q、M在BC上,若BC=12,AD=8,QM
=x,矩形PQMN的面积是__________.(用含x的代数式表示)
第3题图
3. 如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,E为AB上一点,ED,BC的延长线交于点F,∠F=30°,ED=2,DF=6,BE= ,则BC的长为_______.
第4题图
4. 如图,矩形ABCD中,AB=4,AD=6,点E是边CD上一点,
EF⊥AE交BC于点F,则CF长的取值范围是____________.
第5题图
5. 如图,在△ABC中,AB=2,AC= ,D为△ABC内部的一点,且CD⊥BD,在BD的延长线上取一点E,使得∠CAE=∠BAD.若∠ADE
=∠ABC,且∠DBC=30°,则AD的长为________.
第6题图
6. 如图,在Rt△ABC中,∠C=90°,AC=BC,AP、BP分别平分∠CAB、∠CBA,过点P作DE∥AB交AC于点D,交BC于点E.
(1)求证:点P是线段DE的中点;
证明:(1)∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵DE∥AB,
∴∠ABP=∠EPB,∴∠CBP=∠EPB,
∴BE=PE,
同理可证DP=DA,
∵DE∥AB,
∴ ,
∵CA=CB,
∴CE=CD,
∴BE=AD,
∴PE=PD,
∴点P是DE的中点;
第6题图
(2)求证:BP2=BE·BA.
(2)由(1)得∠ABP=∠EBP=∠EPB= ∠CBA,
∵AP平分∠CAB,
∴∠PAB= ∠CAB,
∵CA=CB,
∴∠CBA=∠CAB,
∴∠ABP=∠EBP=∠EPB=∠PAB,
∴△ABP∽△PBE,
∴ ,∴BP2=BA·BE.
第6题图
第7题图①
7. 已知△ABC和△DCE中,AB=AC,DC=DE,BF=EF,点B,C,E都在同一直线上,且△ABC和△DCE在该直线同侧.
(1)如图①,若∠BAC=∠CDE=90°,请猜想线段AF与DF之间的数量关系和位置关系,并证明你的猜想;
解:(1)猜想:AF=DF,AF⊥DF.
证明:如解图,过点A作AH⊥BC于点H,过点D作DJ⊥EC于点J.
H
J
∵AB=AC,DC=DE,∠BAC=∠CDE=90°,
∴BH=CH,CJ=EJ,
∴AH=BH=CH,DJ=CJ=EJ,
∵BF=EF,
∴HJ=BF=EF,
∴BH=FJ=AH,FH=JE=DJ,
∵∠AHF=∠FJD=90°,
∴△AHF≌△FJD(SAS),
∴AF=FD,∠HAF=∠JFD,
第7题图①
H
J
∵∠FAH+∠AFH=90°,
∴∠AFH+∠DFJ=90°,
∴∠AFD=90°,即AF⊥DF;
第7题图①
H
J
(2)如图②,若∠BAC=60°,∠CDE=120°,请直接写出线段AF与DF之间的数量关系和位置关系.
第7题图②
【解法提示】如解图②,过点A作AH⊥BC于点H,过点D作DJ⊥EC于点J.
H
J
∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴BH=CH,AH= BH,
∵DC=DE,∠CDE=120°,
∴CJ=JE,∠DEC=∠DCE=30°,∴JE= DJ,
∵BF=FE,
∴HJ=BF=EF,∴BH=FJ,HF=JE,
∴AH= FJ,FH= DJ,∴ ,
∵∠AHF=∠FJD=90°,
∴△AHF∽△FJD,
∴ ,∠HAF=∠DFJ,
第7题图②
H
J
∵∠FAH+∠AFH=90°,
∴∠AFH+∠DFJ=90°,
∴∠AFD=90°,即AF⊥DF,
∴AF= DF,AF⊥DF.
(2)AF= DF,AF⊥DF.
第7题图②
H
J
同课章节目录
