2024北京中考数学二轮专题复习 微专题 三大常考相似模型 课件(共18张PPT)
文档属性
| 名称 | 2024北京中考数学二轮专题复习 微专题 三大常考相似模型 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
微专题 三大常考相似模型
模型一 A 字型
满分技法
一图多变
例1
(1)如图①,当DE∥BC时,请写出图中的相似三角形______________;
例1题图
△ADE∽△ABC
模型分析
在△ABC中,点D、E分别是AB、AC边上的点.
(3)如图③,当点E与点C重合时,且△ADC∽△ACB,则AC2=______;
AD·AB
例1题图
(2)如图②,当DE与BC不平行时,请添加一个条件________________
_________________,使得△ADE∽△ACB;
∠ADE=∠ACB
或∠AED=∠ABC;
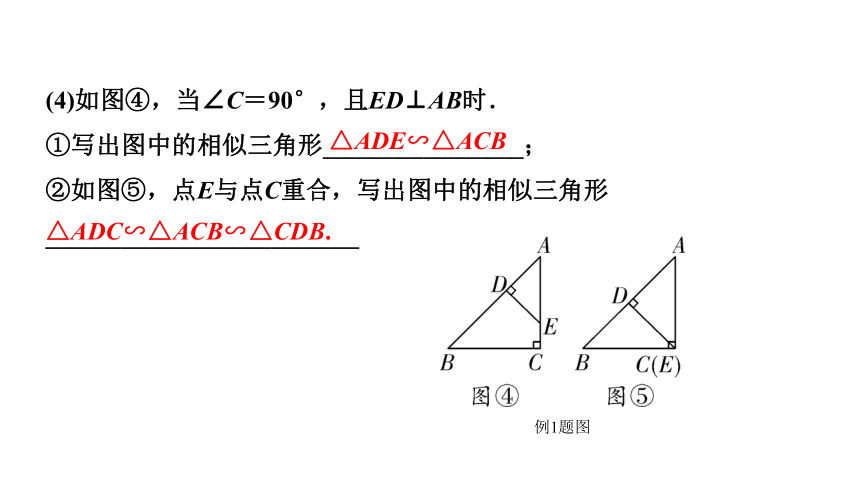
(4)如图④,当∠C=90°,且ED⊥AB时.
①写出图中的相似三角形________________;
②如图⑤,点E与点C重合,写出图中的相似三角形_________________________
△ADC∽△ACB∽△CDB.
△ADE∽△ACB
例1题图
当DE与BC不平行时,该模型叫做斜A字型,
正A字型和斜A字型的特点就是有一组公共角∠A.若要两个三角形相似,需再找一组对应角相等或公共角的两边对应成比例.
当DE∥BC时,该模型叫做正A字型.
第1题图
模型应用
1. 我国古代数学著作《九章算术》中有一道“井深几何”问题,原文如下:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?其大意如图所示(1尺=10寸),则井深为( )
A. 20尺 B. 25尺
C. 57.5尺 D. 62.5尺
C
第2题图
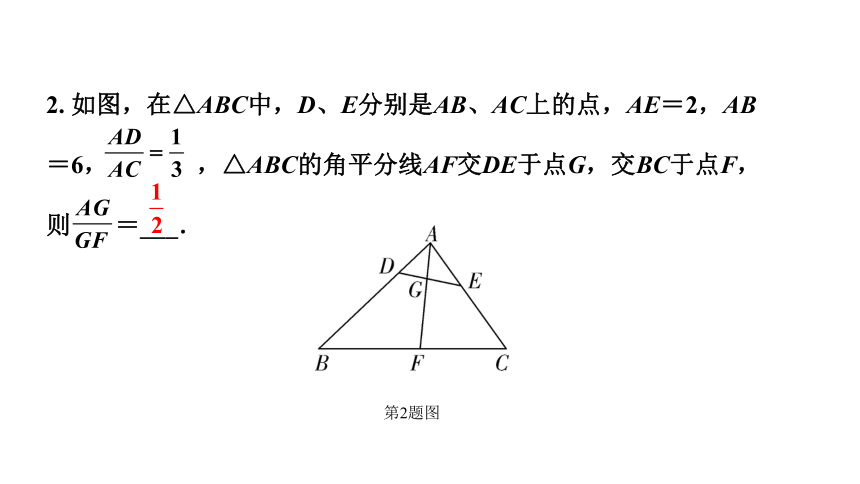
2. 如图,在△ABC中,D、E分别是AB、AC上的点,AE=2,AB=6, ,△ABC的角平分线AF交DE于点G,交BC于点F,则 =___.
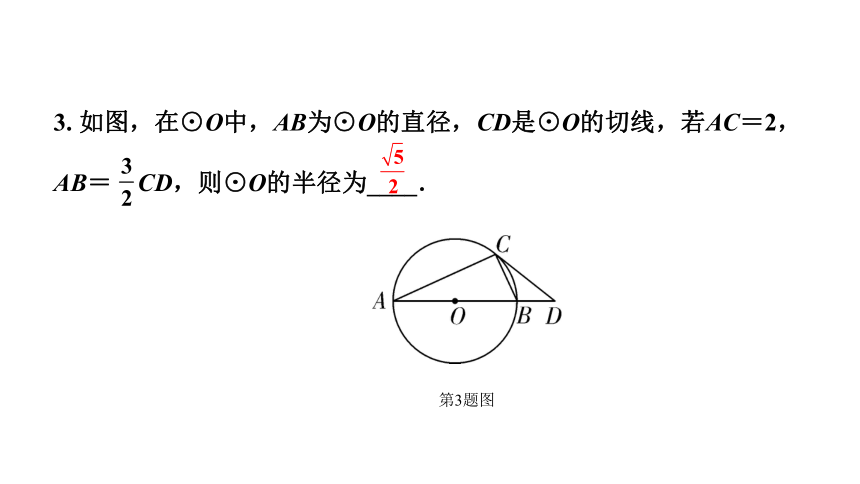
3. 如图,在⊙O中,AB为⊙O的直径,CD是⊙O的切线,若AC=2,AB= CD,则⊙O的半径为____.
第3题图
模型二 8字型
例2 如图,已知AB∥CD,连接AD、BC交于点O,写出图中的相似三角形________________.
例2题图
△ABO∽△DCO
模型分析
例3题图
例3 如图,相交线AD、BC交于点O,连接AB、CD,请添加一个条件________________________________,使得△AOB∽△COD.
∠A=∠C或∠B=∠D或
8字型模型的特点是有一组角为对顶角.若要两个三角形相似,需再找一组对应角相等或对顶角的两边对应成比例.
4. 在 ABCD中,点E是边AD上一点,且AD=3ED,EC交对角线BD于点F,则 的值为_____.
模型应用
5. 如图,AC与BE交于点D,∠A=∠E=90°,若点D是线段AC的中点,且AB=AC=10,则BE的长为______.
第4题图
第5题图
例4 如图,已知△ACP和△BPD,点P在线段AB上,当∠1=∠2=∠3时,求证:△ACP∽△BPD.
例4题图
证明:∵∠1=∠2,∠1+∠C=∠2+∠BPD,
∴∠C=∠BPD.
∵∠1=∠3,
∴△ACP∽△BPD.
模型三 一线三等角型
模型分析
例5 如图,已知Rt△DAB和Rt△BCE,∠A=∠C=90°,点A、B、C在一条直线上,且∠DBE=90°,写出图中的相似三角形_________________
例5题图
△DAB∽△BCE
模型应用
6. 如图,在矩形ABCD中,AB=2,BC=3,若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF的长为________.
第6题图
7. 如图,在△AEC中,B为EC上一点,且满足∠ABD=∠C=∠E.
(1)求证:△AEB∽△BCD;
第7题图
(1)证明:∵∠ABC=∠ABD+∠DBC=∠E+∠EAB,且∠ABD=∠E,
∴∠CBD=∠EAB.
∵∠C=∠E,
∴△AEB∽△BCD;
(2)若 ,AE=2BE=2,求AD的长.
(2)解:∵ ,AE=2BE=2,
∴BC=3,BE=1.
由(1)得△AEB∽△BCD,
∴ ,即 ,
解得CD= .
∵∠C=∠E,∴AC=AE=2,
∴AD=AC-CD=2- = .
第7题图
当点P在AB的延长线上,且满足∠1=∠2=∠3时,
有△ACP∽△BPD.
当∠1、∠2、∠3为钝角时,其基本图形如下:
当一线三等角的角度为90°时,也叫一线三垂直模型(K型),常利用等角的余角相等转换角度证明相似.衍变图形有以下几种:
微专题 三大常考相似模型
模型一 A 字型
满分技法
一图多变
例1
(1)如图①,当DE∥BC时,请写出图中的相似三角形______________;
例1题图
△ADE∽△ABC
模型分析
在△ABC中,点D、E分别是AB、AC边上的点.
(3)如图③,当点E与点C重合时,且△ADC∽△ACB,则AC2=______;
AD·AB
例1题图
(2)如图②,当DE与BC不平行时,请添加一个条件________________
_________________,使得△ADE∽△ACB;
∠ADE=∠ACB
或∠AED=∠ABC;
(4)如图④,当∠C=90°,且ED⊥AB时.
①写出图中的相似三角形________________;
②如图⑤,点E与点C重合,写出图中的相似三角形_________________________
△ADC∽△ACB∽△CDB.
△ADE∽△ACB
例1题图
当DE与BC不平行时,该模型叫做斜A字型,
正A字型和斜A字型的特点就是有一组公共角∠A.若要两个三角形相似,需再找一组对应角相等或公共角的两边对应成比例.
当DE∥BC时,该模型叫做正A字型.
第1题图
模型应用
1. 我国古代数学著作《九章算术》中有一道“井深几何”问题,原文如下:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?其大意如图所示(1尺=10寸),则井深为( )
A. 20尺 B. 25尺
C. 57.5尺 D. 62.5尺
C
第2题图
2. 如图,在△ABC中,D、E分别是AB、AC上的点,AE=2,AB=6, ,△ABC的角平分线AF交DE于点G,交BC于点F,则 =___.
3. 如图,在⊙O中,AB为⊙O的直径,CD是⊙O的切线,若AC=2,AB= CD,则⊙O的半径为____.
第3题图
模型二 8字型
例2 如图,已知AB∥CD,连接AD、BC交于点O,写出图中的相似三角形________________.
例2题图
△ABO∽△DCO
模型分析
例3题图
例3 如图,相交线AD、BC交于点O,连接AB、CD,请添加一个条件________________________________,使得△AOB∽△COD.
∠A=∠C或∠B=∠D或
8字型模型的特点是有一组角为对顶角.若要两个三角形相似,需再找一组对应角相等或对顶角的两边对应成比例.
4. 在 ABCD中,点E是边AD上一点,且AD=3ED,EC交对角线BD于点F,则 的值为_____.
模型应用
5. 如图,AC与BE交于点D,∠A=∠E=90°,若点D是线段AC的中点,且AB=AC=10,则BE的长为______.
第4题图
第5题图
例4 如图,已知△ACP和△BPD,点P在线段AB上,当∠1=∠2=∠3时,求证:△ACP∽△BPD.
例4题图
证明:∵∠1=∠2,∠1+∠C=∠2+∠BPD,
∴∠C=∠BPD.
∵∠1=∠3,
∴△ACP∽△BPD.
模型三 一线三等角型
模型分析
例5 如图,已知Rt△DAB和Rt△BCE,∠A=∠C=90°,点A、B、C在一条直线上,且∠DBE=90°,写出图中的相似三角形_________________
例5题图
△DAB∽△BCE
模型应用
6. 如图,在矩形ABCD中,AB=2,BC=3,若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF的长为________.
第6题图
7. 如图,在△AEC中,B为EC上一点,且满足∠ABD=∠C=∠E.
(1)求证:△AEB∽△BCD;
第7题图
(1)证明:∵∠ABC=∠ABD+∠DBC=∠E+∠EAB,且∠ABD=∠E,
∴∠CBD=∠EAB.
∵∠C=∠E,
∴△AEB∽△BCD;
(2)若 ,AE=2BE=2,求AD的长.
(2)解:∵ ,AE=2BE=2,
∴BC=3,BE=1.
由(1)得△AEB∽△BCD,
∴ ,即 ,
解得CD= .
∵∠C=∠E,∴AC=AE=2,
∴AD=AC-CD=2- = .
第7题图
当点P在AB的延长线上,且满足∠1=∠2=∠3时,
有△ACP∽△BPD.
当∠1、∠2、∠3为钝角时,其基本图形如下:
当一线三等角的角度为90°时,也叫一线三垂直模型(K型),常利用等角的余角相等转换角度证明相似.衍变图形有以下几种:
同课章节目录
