2024年辽宁中考数学二轮专题复习 微专题 常考全等模型 课件(共47张PPT)
文档属性
| 名称 | 2024年辽宁中考数学二轮专题复习 微专题 常考全等模型 课件(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 425.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 15:58:08 | ||
图片预览




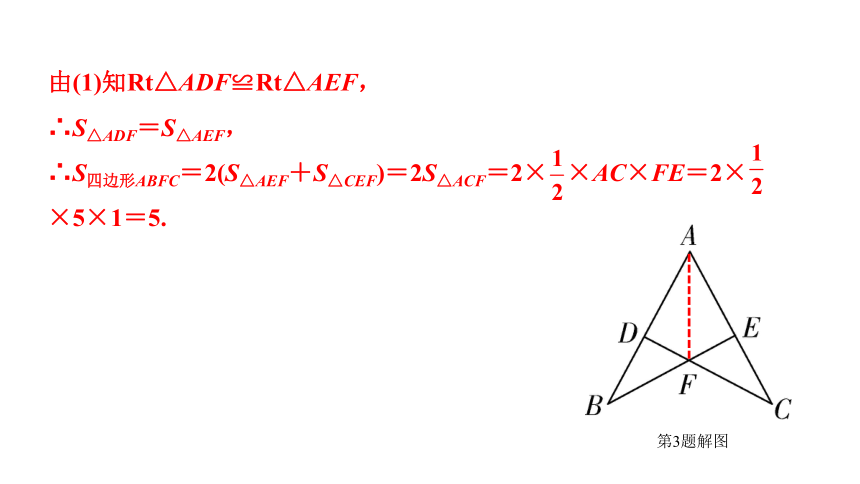

文档简介
(共47张PPT)
微专题 常考全等模型
模型一 平移型
模型分析
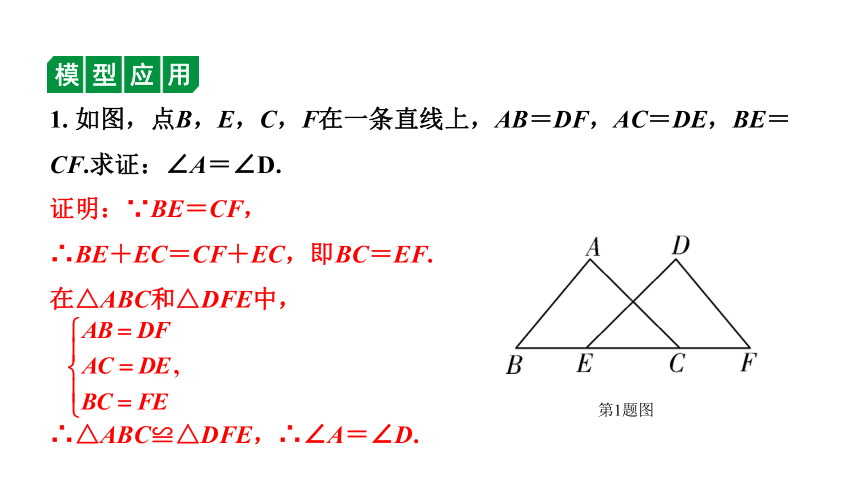
模型展示 已知BE=CF,AB∥DE,AC∥DF.
模型特点 沿同一直线(BC)平移可得两个三角形重合
解题思路 证明三角形全等的关键:(1)加(减)CE,得BC=EF;(2)利用平行线性质找对应角相等
模型应用
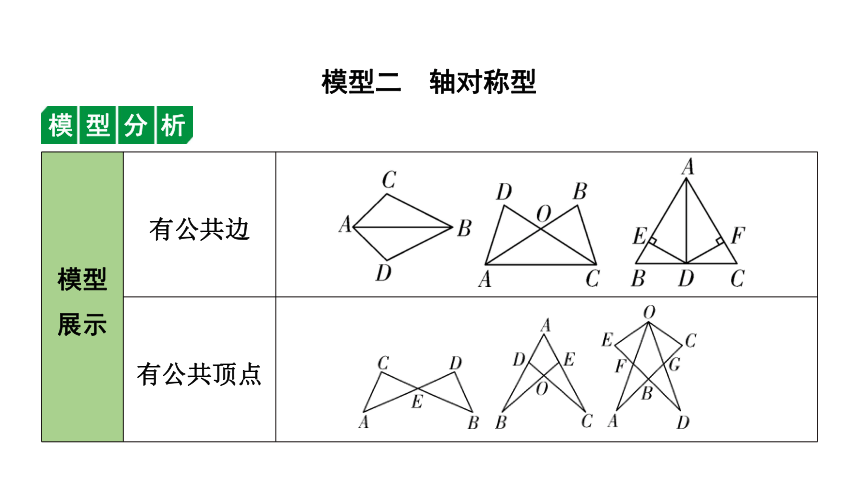
1. 如图,点B,E,C,F在一条直线上,AB=DF,AC=DE,BE=CF.求证:∠A=∠D.
第1题图
证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DFE中,
∴△ABC≌△DFE,∴∠A=∠D.
模型二 轴对称型
模型分析
模型展示 有公共边
有公共顶点
模型特点 所给图形沿公共边所在直线或者经过公共顶点的某条直线折叠,两个三角形完全重合
解题思路 证明三角形全等的关键:(1)找公共角、垂直、对顶角、等腰等条件得对应角相等;(2)找公共边、中点、等底角、相等边、线段的和差等条件得对应边相等
模型应用
2. 如图,四边形ABCD中,AB=AD,AC、BD是对角线,∠1=∠2.求证:△BCD是等腰三角形.
第2题图
证明:在△ABC与△ADC中,
∴△ABC≌△ADC;
∴BC=DC,
∴△BCD是等腰三角形.
3. 如图,已知BE⊥AC,CD⊥AB,垂足分别为E,D,BE与CD相交于点F,FD=FE.
(1)求证:AD=AE;
第3题解图
(1)证明:如解图,连接AF,
∵BE⊥AC,CD⊥AB,FD=FE,
∴∠AEF=∠ADF=90°,
在Rt△ADF和Rt△AEF中,
∴Rt△ADF≌Rt△AEF,∴AD=AE;
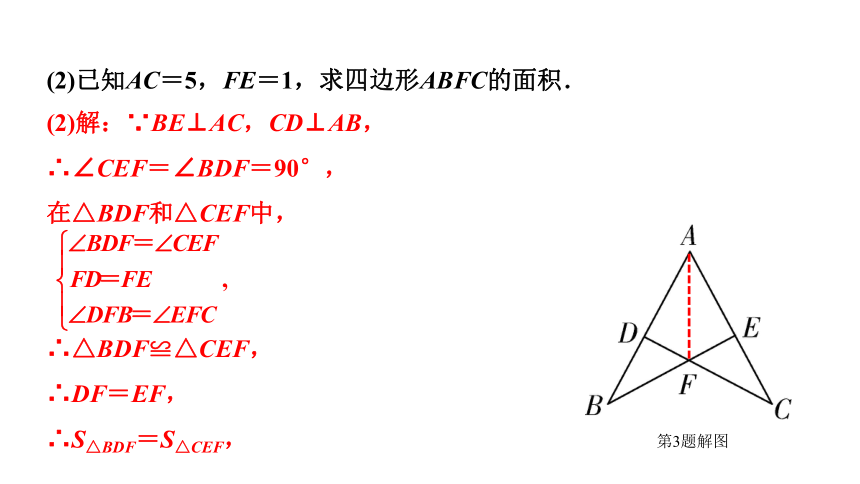
(2)已知AC=5,FE=1,求四边形ABFC的面积.
(2)解:∵BE⊥AC,CD⊥AB,
∴∠CEF=∠BDF=90°,
在△BDF和△CEF中,
∴△BDF≌△CEF,
∴DF=EF,
∴S△BDF=S△CEF,
第3题解图
由(1)知Rt△ADF≌Rt△AEF,
∴S△ADF=S△AEF,
∴S四边形ABFC=2(S△AEF+S△CEF)=2S△ACF=2× ×AC×FE=2× ×5×1=5.
第3题解图
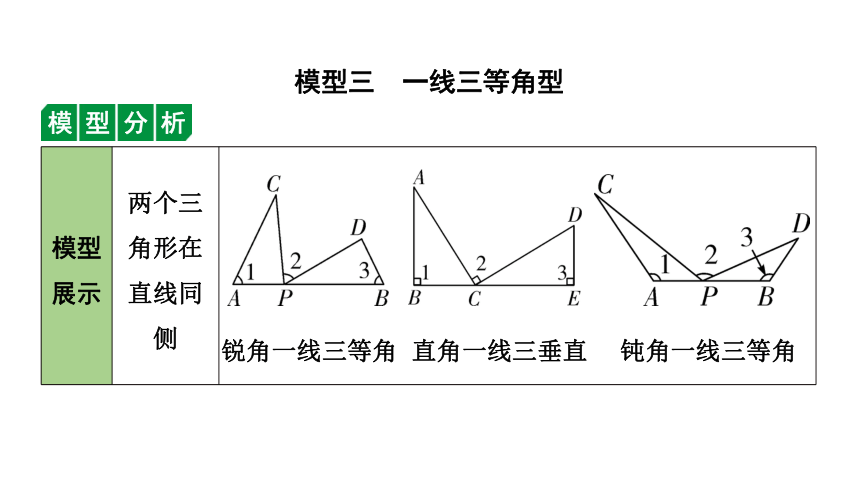
模型三 一线三等角型
模型分析
模型展示 两个三角形在直线同侧
锐角一线三等角
直角一线三垂直
钝角一线三等角
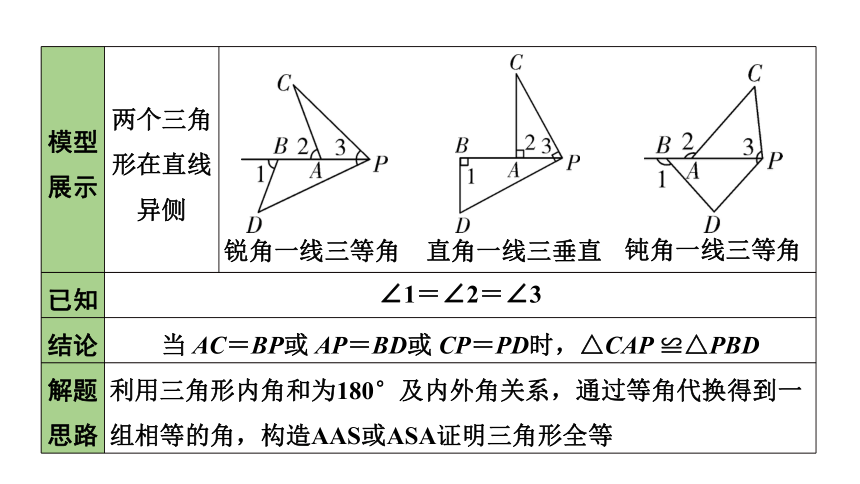
模型展示 两个三角形在直线异侧
已知 ∠1=∠2=∠3 结论 当 AC=BP或 AP=BD或 CP=PD时,△CAP ≌△PBD 解题 思路 利用三角形内角和为180°及内外角关系,通过等角代换得到一组相等的角,构造AAS或ASA证明三角形全等 锐角一线三等角
直角一线三垂直
钝角一线三等角
模型应用
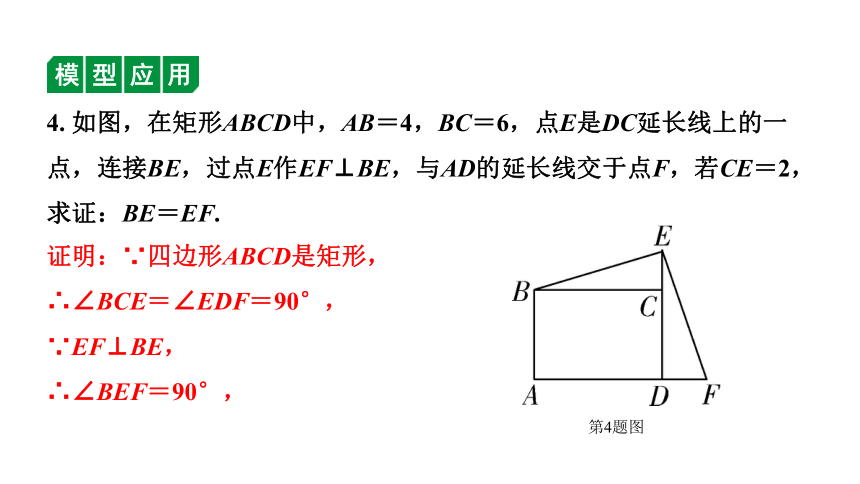
4. 如图,在矩形ABCD中,AB=4,BC=6,点E是DC延长线上的一点,连接BE,过点E作EF⊥BE,与AD的延长线交于点F,若CE=2,求证:BE=EF.
第4题图
证明:∵四边形ABCD是矩形,
∴∠BCE=∠EDF=90°,
∵EF⊥BE,
∴∠BEF=90°,
∵∠CBE+∠BEC=90°,
∠BEC+∠DEF=90°,
∴∠CBE=∠DEF,
∵AB=4,BC=6,CE=2,
∴BC=DE,
在△BCE和△EDF中,
∴△BCE≌△EDF,∴BE=EF.
第4题图
5. 如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.求证:DE=EF.
第5题图
证明:∵∠B+∠BDE+∠BED=180°,∠DEF+∠FEC+∠BED=180°,∠B=∠DEF=60°,
∴∠BDE=∠CEF;
在△BDE和△CEF中,
∴△BDE≌△CEF,∴DE=EF.
模型四 不共顶点旋转型(沈阳4考;抚本铁辽葫5年5考)
模型分析
模型展示 已知BF=CE,AB∥DE,AC∥DF.不共顶点
模型特点 (1)不共顶点旋转问题,绕某一点旋转,再平移可得两三角形重合;(2)共顶点旋转问题(手拉手模型)
解题思路 证明三角形全等的关键:①由BF=CE→BF+CF=CE+CF→BC=EF;②利用平行线性质找对应角相等
模型应用
6. 如图,点B,C,E,F在同一直线上,点A,D在BC的异侧,AB=CD,BF=CE,∠B=∠C.
(1)求证:AE∥DF.
第6题图
(1)证明:∵BF=CE,
∴BF+EF=CE+EF,
即BE=CF,
在△ABE和△DCF中,
∴△ABE≌△DCF,
∴∠AEB=∠DFC,
∴AE∥DF;
第6题图
(2)若∠A+∠D=144°,∠C=30°,求∠AEC的度数.
(2)解:∵△ABE≌△DCF,
∴∠A=∠D,∠B=∠C=30°,
∵∠A+∠D=144°,
∴∠A=72°,
∴∠AEC=∠A+∠B=72°+30°=102°.
第6题图
模型五 共顶点旋转型(手拉手型)
模型分析
模型特点 共顶点:点A;等线段:AB=AC,AD=AE;等角度:∠BAC=∠DAE 模型展示
解题思路 证明三角形全等的关键:(1)共顶点:加(减)共顶点的公共角∠BAE得一组对应角相等;(2)利用已知两组边相等或者等腰、等边、正方形、菱形等得到两组对应边相等
结论 △CAE≌△BAD(SAS),BD=CE,∠BPC=∠BAC(“8字型”证角相等)
模型应用
7. 如图,两个等腰直角△ADC与△EDG,∠ADC=∠EDG=90°,连接AG,CE交于点H.求证:AG=CE.
第7题图
证明:∵△ADC与△EDG是等腰直角三角形,
∴AD=CD,DG=DE,且∠ADC=∠GDE=90°,
∴∠ADG=∠CDE,
在△ADG与△CDE中,
∴△ADG≌△CDE,
∴AG=CE.
第7题图
8. 如图,点P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°,且BQ=BP,连接PQ,CQ.试观察猜想AP与CQ的大小关系,并加以证明.
第8题图
证明如下:∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=60°;
又∵∠PBQ=60°,
∴∠ABC=∠PBQ,
∴∠ABP=∠CBQ;
解:猜想:AP=CQ;
在△ABP和△CBQ中,
∴△ABP≌△CBQ,
∴AP=CQ.
第8题图
模型六 旋转半角型
模型分析
模型特点 AB=AC, ∠BAC=90°, ∠DAE=45° ∠BAD=90°, ∠EAF=45° ∠BDC=120°,
∠EDF=60°
模型展示
解题思路 通过旋转一定角度将另外两个角拼接在一起,构造的三角形与半角所在的三角形全等,得出线段的数量关系 结论 ①△AED≌△AEF; ②△CEF为直角三角形; ③BD2+CE2=DE2 ①△AEF≌△AEG; ②△AGF为等腰直角三角形; ③EF=BE+DF ①△DEF≌△DGF;
②EF=BE+CF
模型应用
9. 在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
第9题图
解:EF=FC+BE,
理由:如解图,过点D作∠CDG=∠BDE,交AN于点G,
G
在△BDE和△CDG中,
∴△BDE≌△CDG,
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
第9题图
G
在△EDF和△GDF中,
∴△EDF≌△GDF.
∴EF=GF,
∴EF=FC+CG=FC+BE.
第9题图
G
模型七 对角互补型
模型分析
模型特点 ∠ABC=∠ADC=90°, AD=CD,BD平分∠ABC ∠ABC=120°,∠ADC=60°,
AD=CD,BD平分∠ABC
模型展示
解题思路 常过顶点作角两边的垂线,构造全等三角形 结论 AB+BC=2BF= AB+BC=2BF=BD
模型应用
10. 在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.点M在AD的延长线上,点N在AC上,连接BM,MN,且∠BMN=90°,求证:AB+AN= AM.
第10题图
证明:如解图,过点M作ME∥BC交AB的延长线于点E,
E
∴∠AME=90°,
∵∠BAC=90°,AB=AC,
∵∠ABC=∠AEM=45°,
则AE= AM,∠E=45°,∴ME=MA,
∵∠AME=90°,∠BMN=90°,
∴∠BME=∠AMN,
在△BME和△NMA中,
∴△BME≌△NMA,
∴BE=NA,
∴AB+AN=AB+BE=AE= AM.
第10题图
E
综合训练
第1题图
1. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,AE=3,BC=5,则DE的长为( )
A. 3 B. 4 C. 5 D. 8
B
第2题图
2. [条件开放性试题]如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF,你添加的条件是_______
_____________________(不再添加辅助线和字母).
∠B=
∠C或∠BED=∠CFD
3. 如图,在△ABC和△CDE中,∠ACB=∠CED=90°,AC=CE,点B是EC的中点,若AB⊥CD于点F,DE=10,则AE的长为______.
第3题图
第4题图
4. 如图,在四边形ABCD中,∠A=∠B=90°,P是AB上一点,连接PC,PD,且PC=PD,∠DPC=90°.
求证:AD+BC=AB.
证明:∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠ADP=∠BPC,
在△ADP与△BPC中,
∴△ADP≌△BPC(AAS),
∴AD=BP,AP=BC,
∴AD+BC=BP+AP=AB,
即AD+BC=AB.
第4题图
第5题图①
5. 在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥BC,交BC延长线于点F.
(1)如图①,当点D为线段AB的上任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;
解:(1)结论:AC=EF+FC,
证明:如解图①,过点D作DH⊥CB于点H,
H
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
在△FEC和△HDC中,
∴△FEC≌△HDC,∴FC=HC,EF=DH,
∵∠DHB=90°,∠B=45°,
∴DH=HB=EF,
∴AC=BC=CH+BH=FC+EF;
第5题图①
H
(2)如图②,当点D为线段BA的延长线上一点时,依题意补全图②,猜想线段EF、CF、AC的数量关系是否发生改变,并证明.
(2)依题意补全图形如解图②,结论:EF=FC+AC,
理由如下:如解图②,过点D作DH⊥CB交BC的延长线于点H,
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
第5题图
解图②
在△FEC和△HDC中,
∴△EFC≌△DHC,
∴FC=HC,EF=DH,
∵∠DHB=90°,∠B=45°,
∴DH=HB=EF,
∴EF=CH+BC=FC+AC.
解图②
6. 如图,点C为线段BD上一点,△ABC、△CDE都是等边三角形.AD与CE交于点F,BE与AC交于点G.
(1)求证:△ACD≌△BCE;
(1)证明:∵△ABC,△CDE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
∴△ACD≌△BCE;
第6题图
(2)若CF+CG=8,BD=18,求△ACD的面积.
(2)解:由(1)得△ACD≌△BCE,
∴∠CBG=∠CAF,
又∵∠ACF=∠BCG=60°,BC=AC,
∴△BCG≌△ACF,
∴S△ACF=S△BCG,CG=CF,而CF+CG=8,
∴CG=CF=4,
第6题图
第6题图
M
N
如解图,过点G作GM⊥BD于点M,过点F作FN⊥BD于点N,
又∵∠ACB=∠DCE=60°,
∴GM= CG= ,FN= CF= ,
∴S△ACD=S△ACF+S△CDF
=S△BCG+S△CDF
= BC·GM+ CD·FN
= × ×(BC+CD)
= BD=18 .
第7题图
7. 如图,在△ABC中,AB=AC,AB>BC.点D在边BC上,点E、F在线段AD上,∠1=∠2=∠BAC.
(1)求证:BE=AF;
(1)证明:∵∠1=∠BAE+∠ABE,∠1=∠BAC,
∴∠BAC=∠BAE+∠ABE,
∵∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF,
∵∠1=∠BAE+∠ABE,∠2=∠CAF+∠ACF,∠1=∠2,
∴∠BAE=∠ACF,
∵AB=AC,
在△BAE和△ACF中,
∴△BAE≌△ACF,
∴BE=AF;
第7题图
(2)若CD=2BD,△ABC的面积为15,求△ACF与△BDE的面积之和.
(2)解:由(1)知△BAE≌△ACF,
∴S△BAE=S△ACF,
∵CD=2BD,S△ABC=15,
∴S△ABD= ×15=5,
∴S△ACF+S△BDE=S△BAE+S△BDE=S△ABD=5.
∴△ACF与△BDE的面积之和为5.
第7题图
微专题 常考全等模型
模型一 平移型
模型分析
模型展示 已知BE=CF,AB∥DE,AC∥DF.
模型特点 沿同一直线(BC)平移可得两个三角形重合
解题思路 证明三角形全等的关键:(1)加(减)CE,得BC=EF;(2)利用平行线性质找对应角相等
模型应用
1. 如图,点B,E,C,F在一条直线上,AB=DF,AC=DE,BE=CF.求证:∠A=∠D.
第1题图
证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DFE中,
∴△ABC≌△DFE,∴∠A=∠D.
模型二 轴对称型
模型分析
模型展示 有公共边
有公共顶点
模型特点 所给图形沿公共边所在直线或者经过公共顶点的某条直线折叠,两个三角形完全重合
解题思路 证明三角形全等的关键:(1)找公共角、垂直、对顶角、等腰等条件得对应角相等;(2)找公共边、中点、等底角、相等边、线段的和差等条件得对应边相等
模型应用
2. 如图,四边形ABCD中,AB=AD,AC、BD是对角线,∠1=∠2.求证:△BCD是等腰三角形.
第2题图
证明:在△ABC与△ADC中,
∴△ABC≌△ADC;
∴BC=DC,
∴△BCD是等腰三角形.
3. 如图,已知BE⊥AC,CD⊥AB,垂足分别为E,D,BE与CD相交于点F,FD=FE.
(1)求证:AD=AE;
第3题解图
(1)证明:如解图,连接AF,
∵BE⊥AC,CD⊥AB,FD=FE,
∴∠AEF=∠ADF=90°,
在Rt△ADF和Rt△AEF中,
∴Rt△ADF≌Rt△AEF,∴AD=AE;
(2)已知AC=5,FE=1,求四边形ABFC的面积.
(2)解:∵BE⊥AC,CD⊥AB,
∴∠CEF=∠BDF=90°,
在△BDF和△CEF中,
∴△BDF≌△CEF,
∴DF=EF,
∴S△BDF=S△CEF,
第3题解图
由(1)知Rt△ADF≌Rt△AEF,
∴S△ADF=S△AEF,
∴S四边形ABFC=2(S△AEF+S△CEF)=2S△ACF=2× ×AC×FE=2× ×5×1=5.
第3题解图
模型三 一线三等角型
模型分析
模型展示 两个三角形在直线同侧
锐角一线三等角
直角一线三垂直
钝角一线三等角
模型展示 两个三角形在直线异侧
已知 ∠1=∠2=∠3 结论 当 AC=BP或 AP=BD或 CP=PD时,△CAP ≌△PBD 解题 思路 利用三角形内角和为180°及内外角关系,通过等角代换得到一组相等的角,构造AAS或ASA证明三角形全等 锐角一线三等角
直角一线三垂直
钝角一线三等角
模型应用
4. 如图,在矩形ABCD中,AB=4,BC=6,点E是DC延长线上的一点,连接BE,过点E作EF⊥BE,与AD的延长线交于点F,若CE=2,求证:BE=EF.
第4题图
证明:∵四边形ABCD是矩形,
∴∠BCE=∠EDF=90°,
∵EF⊥BE,
∴∠BEF=90°,
∵∠CBE+∠BEC=90°,
∠BEC+∠DEF=90°,
∴∠CBE=∠DEF,
∵AB=4,BC=6,CE=2,
∴BC=DE,
在△BCE和△EDF中,
∴△BCE≌△EDF,∴BE=EF.
第4题图
5. 如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.求证:DE=EF.
第5题图
证明:∵∠B+∠BDE+∠BED=180°,∠DEF+∠FEC+∠BED=180°,∠B=∠DEF=60°,
∴∠BDE=∠CEF;
在△BDE和△CEF中,
∴△BDE≌△CEF,∴DE=EF.
模型四 不共顶点旋转型(沈阳4考;抚本铁辽葫5年5考)
模型分析
模型展示 已知BF=CE,AB∥DE,AC∥DF.不共顶点
模型特点 (1)不共顶点旋转问题,绕某一点旋转,再平移可得两三角形重合;(2)共顶点旋转问题(手拉手模型)
解题思路 证明三角形全等的关键:①由BF=CE→BF+CF=CE+CF→BC=EF;②利用平行线性质找对应角相等
模型应用
6. 如图,点B,C,E,F在同一直线上,点A,D在BC的异侧,AB=CD,BF=CE,∠B=∠C.
(1)求证:AE∥DF.
第6题图
(1)证明:∵BF=CE,
∴BF+EF=CE+EF,
即BE=CF,
在△ABE和△DCF中,
∴△ABE≌△DCF,
∴∠AEB=∠DFC,
∴AE∥DF;
第6题图
(2)若∠A+∠D=144°,∠C=30°,求∠AEC的度数.
(2)解:∵△ABE≌△DCF,
∴∠A=∠D,∠B=∠C=30°,
∵∠A+∠D=144°,
∴∠A=72°,
∴∠AEC=∠A+∠B=72°+30°=102°.
第6题图
模型五 共顶点旋转型(手拉手型)
模型分析
模型特点 共顶点:点A;等线段:AB=AC,AD=AE;等角度:∠BAC=∠DAE 模型展示
解题思路 证明三角形全等的关键:(1)共顶点:加(减)共顶点的公共角∠BAE得一组对应角相等;(2)利用已知两组边相等或者等腰、等边、正方形、菱形等得到两组对应边相等
结论 △CAE≌△BAD(SAS),BD=CE,∠BPC=∠BAC(“8字型”证角相等)
模型应用
7. 如图,两个等腰直角△ADC与△EDG,∠ADC=∠EDG=90°,连接AG,CE交于点H.求证:AG=CE.
第7题图
证明:∵△ADC与△EDG是等腰直角三角形,
∴AD=CD,DG=DE,且∠ADC=∠GDE=90°,
∴∠ADG=∠CDE,
在△ADG与△CDE中,
∴△ADG≌△CDE,
∴AG=CE.
第7题图
8. 如图,点P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°,且BQ=BP,连接PQ,CQ.试观察猜想AP与CQ的大小关系,并加以证明.
第8题图
证明如下:∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=60°;
又∵∠PBQ=60°,
∴∠ABC=∠PBQ,
∴∠ABP=∠CBQ;
解:猜想:AP=CQ;
在△ABP和△CBQ中,
∴△ABP≌△CBQ,
∴AP=CQ.
第8题图
模型六 旋转半角型
模型分析
模型特点 AB=AC, ∠BAC=90°, ∠DAE=45° ∠BAD=90°, ∠EAF=45° ∠BDC=120°,
∠EDF=60°
模型展示
解题思路 通过旋转一定角度将另外两个角拼接在一起,构造的三角形与半角所在的三角形全等,得出线段的数量关系 结论 ①△AED≌△AEF; ②△CEF为直角三角形; ③BD2+CE2=DE2 ①△AEF≌△AEG; ②△AGF为等腰直角三角形; ③EF=BE+DF ①△DEF≌△DGF;
②EF=BE+CF
模型应用
9. 在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
第9题图
解:EF=FC+BE,
理由:如解图,过点D作∠CDG=∠BDE,交AN于点G,
G
在△BDE和△CDG中,
∴△BDE≌△CDG,
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
第9题图
G
在△EDF和△GDF中,
∴△EDF≌△GDF.
∴EF=GF,
∴EF=FC+CG=FC+BE.
第9题图
G
模型七 对角互补型
模型分析
模型特点 ∠ABC=∠ADC=90°, AD=CD,BD平分∠ABC ∠ABC=120°,∠ADC=60°,
AD=CD,BD平分∠ABC
模型展示
解题思路 常过顶点作角两边的垂线,构造全等三角形 结论 AB+BC=2BF= AB+BC=2BF=BD
模型应用
10. 在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.点M在AD的延长线上,点N在AC上,连接BM,MN,且∠BMN=90°,求证:AB+AN= AM.
第10题图
证明:如解图,过点M作ME∥BC交AB的延长线于点E,
E
∴∠AME=90°,
∵∠BAC=90°,AB=AC,
∵∠ABC=∠AEM=45°,
则AE= AM,∠E=45°,∴ME=MA,
∵∠AME=90°,∠BMN=90°,
∴∠BME=∠AMN,
在△BME和△NMA中,
∴△BME≌△NMA,
∴BE=NA,
∴AB+AN=AB+BE=AE= AM.
第10题图
E
综合训练
第1题图
1. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,AE=3,BC=5,则DE的长为( )
A. 3 B. 4 C. 5 D. 8
B
第2题图
2. [条件开放性试题]如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF,你添加的条件是_______
_____________________(不再添加辅助线和字母).
∠B=
∠C或∠BED=∠CFD
3. 如图,在△ABC和△CDE中,∠ACB=∠CED=90°,AC=CE,点B是EC的中点,若AB⊥CD于点F,DE=10,则AE的长为______.
第3题图
第4题图
4. 如图,在四边形ABCD中,∠A=∠B=90°,P是AB上一点,连接PC,PD,且PC=PD,∠DPC=90°.
求证:AD+BC=AB.
证明:∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠ADP=∠BPC,
在△ADP与△BPC中,
∴△ADP≌△BPC(AAS),
∴AD=BP,AP=BC,
∴AD+BC=BP+AP=AB,
即AD+BC=AB.
第4题图
第5题图①
5. 在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥BC,交BC延长线于点F.
(1)如图①,当点D为线段AB的上任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;
解:(1)结论:AC=EF+FC,
证明:如解图①,过点D作DH⊥CB于点H,
H
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
在△FEC和△HDC中,
∴△FEC≌△HDC,∴FC=HC,EF=DH,
∵∠DHB=90°,∠B=45°,
∴DH=HB=EF,
∴AC=BC=CH+BH=FC+EF;
第5题图①
H
(2)如图②,当点D为线段BA的延长线上一点时,依题意补全图②,猜想线段EF、CF、AC的数量关系是否发生改变,并证明.
(2)依题意补全图形如解图②,结论:EF=FC+AC,
理由如下:如解图②,过点D作DH⊥CB交BC的延长线于点H,
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
第5题图
解图②
在△FEC和△HDC中,
∴△EFC≌△DHC,
∴FC=HC,EF=DH,
∵∠DHB=90°,∠B=45°,
∴DH=HB=EF,
∴EF=CH+BC=FC+AC.
解图②
6. 如图,点C为线段BD上一点,△ABC、△CDE都是等边三角形.AD与CE交于点F,BE与AC交于点G.
(1)求证:△ACD≌△BCE;
(1)证明:∵△ABC,△CDE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
∴△ACD≌△BCE;
第6题图
(2)若CF+CG=8,BD=18,求△ACD的面积.
(2)解:由(1)得△ACD≌△BCE,
∴∠CBG=∠CAF,
又∵∠ACF=∠BCG=60°,BC=AC,
∴△BCG≌△ACF,
∴S△ACF=S△BCG,CG=CF,而CF+CG=8,
∴CG=CF=4,
第6题图
第6题图
M
N
如解图,过点G作GM⊥BD于点M,过点F作FN⊥BD于点N,
又∵∠ACB=∠DCE=60°,
∴GM= CG= ,FN= CF= ,
∴S△ACD=S△ACF+S△CDF
=S△BCG+S△CDF
= BC·GM+ CD·FN
= × ×(BC+CD)
= BD=18 .
第7题图
7. 如图,在△ABC中,AB=AC,AB>BC.点D在边BC上,点E、F在线段AD上,∠1=∠2=∠BAC.
(1)求证:BE=AF;
(1)证明:∵∠1=∠BAE+∠ABE,∠1=∠BAC,
∴∠BAC=∠BAE+∠ABE,
∵∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF,
∵∠1=∠BAE+∠ABE,∠2=∠CAF+∠ACF,∠1=∠2,
∴∠BAE=∠ACF,
∵AB=AC,
在△BAE和△ACF中,
∴△BAE≌△ACF,
∴BE=AF;
第7题图
(2)若CD=2BD,△ABC的面积为15,求△ACF与△BDE的面积之和.
(2)解:由(1)知△BAE≌△ACF,
∴S△BAE=S△ACF,
∵CD=2BD,S△ABC=15,
∴S△ABD= ×15=5,
∴S△ACF+S△BDE=S△BAE+S△BDE=S△ABD=5.
∴△ACF与△BDE的面积之和为5.
第7题图
同课章节目录
