14.4用样本估计总体 同步练习(含解析)2023——2024学年苏教版(2019)高中数学必修第二册
文档属性
| 名称 | 14.4用样本估计总体 同步练习(含解析)2023——2024学年苏教版(2019)高中数学必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 16:32:46 | ||
图片预览




文档简介
14.4用样本估计总体 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某同学一学期七次模拟考试数学成绩(满分150分)依次为88,98,112,106,122,118,110,则这名同学七次数学成绩的分位数为( )
A.110 B.112 C.115 D.118
2.研究人员测量了某种药物服用8小时后在人体血液中所占的百分比,并将所得数据统计如下图所示,据此可以估计,这种药物服用8小时后在人体血液中所占百分比的中位数为( )
A.6 B.5.5 C.5.2 D.6.5
3.2023年10月4日,在杭州亚运会跳水男子10米台决赛中,中国选手杨昊夺得金牌.中国跳水队包揽杭州亚运会跳水项目全部10枚金牌.跳水比赛的评分规则如下,7位裁判同时给分,去掉两个最高分,去掉两个最低分,剩下的3个分数求和再乘以难度系数,就是该选手本轮的得分,下表就是杨昊比赛中的第一轮得分表,则( )
1号 裁判 2号 裁判 3号 裁判 4号 裁判 5号 裁判 6号 裁判 7号 裁判 难度 系数 本轮 得分
a 9.5 9.0 10.0 9.5 10.0 10.0 3.2 92.80
A.这7个数据的众数只能是10.0
B.这7个数据的中位数只能是9.0
C.a可能是10.0
D.a可能是9.5
4.某机构统计了中国2018—2022年全部工业增加值(单位:万亿元)及增长率数据如图所示,则下列结论错误的是( )
A.2018—2022年中国的全部工业增加值逐年增加
B.2018—2022年中国全部工业增加值的增长率的极差为
C.与上一年相比,2022年中国增加的全部工业增加值是2019年增加的全部工业增加值的2倍
D.2018年中国全部工业增加值的增长率比2018—2022年中国全部工业增加值的增长率的最小值高
5.某机构统计的我国2018-2022年工业增加值及其增长率数据如图所示,则下列结论错误的是( )
2018-2022年工业增加值及其增长率
A.2018-2022年我国的工业增加值逐年增加
B.2018-2022年我国工业增加值的增长率的极差为
C.我国2022年比上一年增加的工业增加值是2019年比上一年增加的工业增加值的2倍
D.我国2018年工业增加值的增长率比2018-2022年工业增加值的最低增长率高
6.某10人的射击小组,在一次射击训练中射击成绩数据如下表,则这组数据的中位数为( )
成绩(单位:环) 6 7 8 9 10
人数 1 2 2 4 1
A.2 B.8 C.8.2 D.8.5
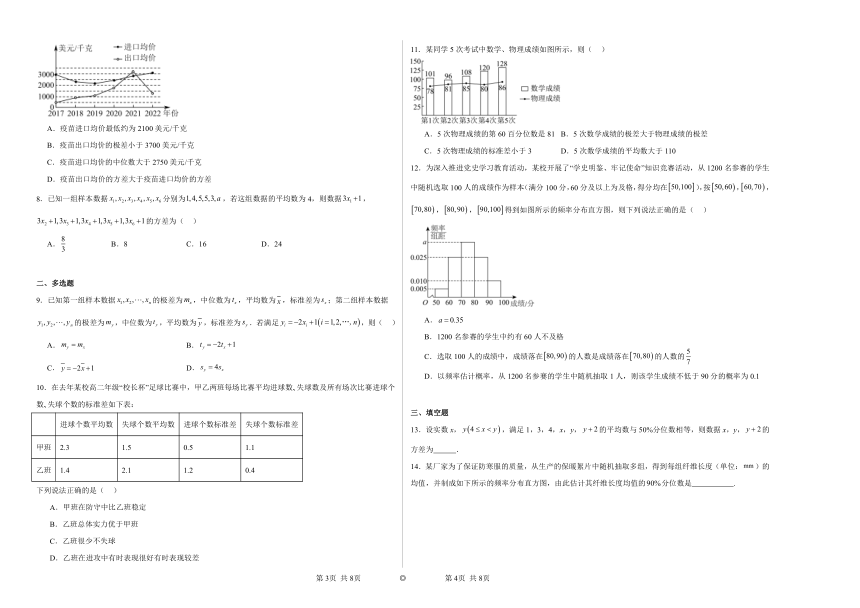
7.如图是我国2017~2022年人用疫苗进出口均价,下列结论不正确的是( )
A.疫苗进口均价最低约为2100美元/千克
B.疫苗出口均价的极差小于3700美元/千克
C.疫苗进口均价的中位数大于2750美元/千克
D.疫苗出口均价的方差大于疫苗进口均价的方差
8.已知一组样本数据分别为,若这组数据的平均数为4,则数据,的方差为( )
A. B.8 C.16 D.24
二、多选题
9.已知第一组样本数据的极差为,中位数为,平均数为,标准差为;第二组样本数据的极差为,中位数为,平均数为,标准差为.若满足,则( )
A. B.
C. D.
10.在去年某校高二年级“校长杯”足球比赛中,甲乙两班每场比赛平均进球数 失球数及所有场次比赛进球个数 失球个数的标准差如下表:
进球个数平均数 失球个数平均数 进球个数标准差 失球个数标准差
甲班 2.3 1.5 0.5 1.1
乙班 1.4 2.1 1.2 0.4
下列说法正确的是( )
A.甲班在防守中比乙班稳定
B.乙班总体实力优于甲班
C.乙班很少不失球
D.乙班在进攻中有时表现很好有时表现较差
11.某同学5次考试中数学、物理成绩如图所示,则( )
A.5次物理成绩的第60百分位数是81 B.5次数学成绩的极差大于物理成绩的极差
C.5次物理成绩的标准差小于3 D.5次数学成绩的平均数大于110
12.为深入推进党史学习教育活动,某校开展了“学史明鉴、牢记使命”知识竞赛活动,从1200名参赛的学生中随机选取100人的成绩作为样本(满分100分,60分及以上为及格,得分均在),按,,,,得到如图所示的频率分布直方图,则下列说法正确的是( )
A.
B.1200名参赛的学生中约有60人不及格
C.选取100人的成绩中,成绩落在的人数是成绩落在的人数的
D.以频率估计概率,从1200名参赛的学生中随机抽取1人,则该学生成绩不低于90分的概率为0.1
三、填空题
13.设实数x,,满足1,3,4,x,y,的平均数与50%分位数相等,则数据x,y,的方差为 .
14.某厂家为了保证防寒服的质量,从生产的保暖絮片中随机抽取多组,得到每组纤维长度(单位:)的均值,并制成如下所示的频率分布直方图,由此估计其纤维长度均值的分位数是 .
15.某班成立了两个数学兴趣小组,组人,组人,经过一周的补习后进行了一次测试,在该测试中,组的平均成绩为分,方差为,组的平均成绩为分,方差为.则在这次测试中全班学生方差为 .
16.已知统计某校1 000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数a的值是 .
四、解答题
17.2023年7月底,受台风杜苏芮影响,京津冀多地出现了特大暴雨,给当地群众的生命和财产造成了重大损失.某村为了了解该村受灾村民的经济损失情况,以便制定合理的帮扶方案,抽调人员进行调查并将该村所有受灾村民的经济损失情况统计如下图所示.
(1)求的值;
(2)求该村所有受灾村民的经济损失的平均值;
(3)现按照分层随机抽样的方法从经济损失在的村民中随机抽取8人,则经济损失在的村民有多少人?
18.随着人们生活水平的提高,对零食的需求也在增加,特别是在年轻人群中,零食已经成为他们日常消费的一部分,新兴的消费群体和消费观念为零食集合店的发展提供了巨大的机会和包容性某公司为了了解青少年消费者对甲、乙两个品牌零食集合店的满意程度,统计了10名青少年消费者对这两个品牌零食集合店的打分(满分10分),结果如下:
甲品牌零食集合店 6 10 7 9 6 5 6 8 8 5
乙品牌零食集合店 5 9 5 4 5 7 10 9 8 8
(1)求样本平均数和方差;
(2)判断青少年消费者对甲、乙两个品牌零食集合店的满意度是否有明显差异(若,则认为青少年消费者对甲、乙两个品牌零食集合店的满意度无明显差异,否则认为有明显差异).
19.某杨梅种植户从购买客户中随机抽取20位客户做质量随访调查,其中购买系列(大棚种植)的10位,购买系列(自然种植)的10位,从杨梅的大小、口感、水分、甜度进行综合打分(满分100分),打分结果记录如下:
系列(大棚种植):84 81 79 76 95 88 93 86 86 92
系列(自然种植):92 95 80 75 83 87 90 80 85 93
(1)分别写出这两个系列综合打分的中位数.
(2)分别求出这两个系列综合打分的平均数与方差,通过上述数据结果进行分析,你认为推广哪种系列种植更合适?
20.某高校共有“机器人”兴趣团队20个,将这20个团队分为甲 乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲 乙两组的成绩如下(单位:分):
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
学校计划从甲、乙两组中选一组参加机器人大赛,从统计学角度分析,若最终选择甲组,理由是什么?若最终选择乙组,理由是什么?
21.随机抽取100名男学生,测得他们的身高(单位:cm),按照区间,,,,分组,得到样本身高的频率分布直方图如图所示
(1)求这100名男学生身高在170cm及以上的学生人数;
(2)估计该校100名学生身高的75%分位数.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】将某同学一学期七次模拟考试数学成绩从低到高排列,根据百分位数的概念,即可求得答案.
【详解】将某同学一学期七次模拟考试数学成绩从低到高排列依次为88,98,106,110,112,118,122,
由于,故这名同学七次数学成绩的分位数为第6个数,即118,
故选:D
2.A
【分析】根据频率分布直方图的特征求出a,结合中位数的定义即可求解.
【详解】依题意,,解得,
则前三块小矩形的面积分别为,,,
所以中位数位于组内,则所求中位数为.
故选:A.
3.D
【分析】根据评分规则,结合众数、中位数的定义进行求解即可.
【详解】当时,由题意可知:,符合题意,此时众数为10或(此时),中位数为9.5,因此选项AB不正确,D正确;
当时,由题意可知:,舍去,因此选项C不正确,
故选:D
4.C
【分析】根据统计图表中的数据,结合每个选项,进行逐一分析,即可判断和选择.
【详解】对A:由条形图知,2018—2022年中国的全部工业增加值逐年增加,故A正确;
对B:由折线图知,2018—2022年中国全部工业增加值的增长率的极差为,故B正确;
对C:由条形图知,与上一年相比,2022年中国增加的全部工业增加值为,
2019年增加的全部工业增加值为,不是2倍关系,故C错误;
对D:由条形图知,2018年中国全部工业增加值的增长率为,
2018—2022年中国全部工业增加值的增长率的最小值为,,故D正确.
故选:C.
5.C
【分析】根据条形图,结合统计相关知识逐项分析判断.
【详解】对于A:由条形图知,2018-2022年我国的工业增加值逐年增加,故A正确;
对于B:由折线图知,2018-2022年我国工业增加值的增长率的极差为,故B正确;
对于C:由条形图知,我国2022年比上一年增加的工业增加值为(万亿元),
2019年比上一年增加的工业增加值为(万亿元),不是2倍关系,故C错误;
对于D:由条形图知,我国2018年工业增加值的增长率为,2018-2022年工业增加值的最低增长率为,
且,故D正确.
故选:C.
6.D
【分析】利用中位数的定义即可得解.
【详解】将射击成绩由小到大排列:,
第个数分别为,因而中位数为.
故选:D.
7.C
【分析】根据图表观察可确定ABD选项,由中位数的定义确定中位数为2019年、2020年的疫苗进口均价的平均数,观察范围即可确定.
【详解】由题图易知选项A,B正确;
对于选项C,疫苗进口均价的中位数是2020年与2021年疫苗进口均价的平均数,2020年的疫苗进口均价小于2500美元/千克,2021年的疫苗进口均价小于3000美元/千克,因此中位数小于2750美元/千克,故选项C不正确;
对于选项D,由题图易知疫苗出口均价波动幅度比疫苗进口均价波动幅度大,所以疫苗出口均价的方差大于疫苗进口均价的方差,故选项D正确.
故选:C.
8.D
【分析】先求出,再结合方差公式可得正确选项.
【详解】由题设有,故,
故,
故数据,的方差为:
,
故选:D.
9.BC
【分析】利用极差的定义可判断A选项;利用中位数的定义可判断B选项;利用平均数公式可判断C选项;利用方差公式可判断D选项.
【详解】解:因为,
对于A,设在数据中最大,最小,则,
则在数据中最大,最小,则,故A错误;
对于B,因为样本数据的中位数为,
当为偶数时,,
又因为,
所以样本数据的中位数为,
当为奇数时,,
又因为,
所以样本数据的中位数为,
所以样本数据的中位数为,故B正确;
对于C,因为样本数据的平均数为 ,
即 ,
所以样本数据的平均数为
,故C正确;
对于D,因为样本数据的标准差为,
样本数据的标准差为 ,
则,
,
,
所以,故D错误.
故选:BC.
10.CD
【分析】由平均数及标准差的大小关系逐一判断各选项.
【详解】由失球个数的标准差可得A错误;
由进球个数和失球个数的平均数可得B错误;
由失球个数的标准差可知C正确;
由进球个数的标准差可知D正确.
故选:CD
11.BD
【分析】根据百分位数,极差,标准差,平均数的计算公式依次得出答案.
【详解】由题知,5次数学成绩从低到高依次排列为:96、101、108、120、128,
5次物理成绩从低到高依次排列为:78、80、81、85、86.
对于A选项,因为,所以5次物理成绩的第60百分位数为,故A选项错误;
对于B选项,5次数学成绩的极差为,5次物理成绩的极差为,数学成绩的极差大于物理成绩的极差,故B选项正确;
对于C选项,5次物理成绩的平均数为,
标准差为,
故C选项错误;
对于D选项,5次数学成绩的平均数为,
平均数大于110,故D选项正确.
故选:BD.
12.BCD
【分析】对于A,利用各小矩形的面积之和为1求解即可;对于B,根据频率分布直方图得到分数小于60的频率,从而求得1200名参赛的学生中不及格的人数;对于C,分别计算出成绩落在的人数和成绩落在的人数,即可判断;对于D,根据频率分布直方图得学生成绩不低于90分的频率,从而得到答案.
【详解】对于A,由,得,故A错误;
对于B,1200名参赛的学生中不及格的人数为,故B正确;
对于C,选取100人的成绩中,成绩落在的人数为,成绩落在的人数为,则成绩落在的人数是成绩落在的人数的,故C正确;
对于D,以频率估计概率,从1200名参赛的学生中随机抽取1人,则该学生成绩不低于90分的概率为,故D正确.
故选:BCD.
13./
【分析】利用平均数与分位数相等,得,代入数据中得方差.
【详解】根据题意,数据的平均数为,
数据的分位数为,
∴ ,即,代入数据,
即为,此组数据的平均数为,
∴ 数据的方差为.
故答案:
14.36
【分析】计算前6个以及前面7个矩形面积之和,确定纤维长度均值的分位数位于第7组内,根据分位数的含义,列式计算,即得答案.
【详解】由频率分布直方图可得从左到右前6个矩形面积之和为:,
前7个矩形面积之和为,
故纤维长度均值的分位数位于第7组内,
设纤维长度均值的分位数为x,则,
解得,
即估计其纤维长度均值的分位数是36,
故答案为:36
15.
【分析】利用各层方差与总体方差之间的关系式可求全班学生方差.
【详解】依题意,,,,
∴(分),
∴全班学生的平均成绩为分.
全班学生成绩的方差为
故答案为:
16.0.020
【详解】
由频率分布直方图的性质,得10(0.005+0.015+a+0.035+0.015+0.010)=1,解得a=0.020.
17.(1)
(2)3360(元)
(3)6人
【分析】(1)由频率分布直方图中各矩形的面积之和为1列方程即可求解;
(2)由频率分布直方图中的平均数计算公式直接运算即可求解;
(3)首先算出经济损失在和在的人数比例,根据分层抽样的抽取方法直接计算即可求解.
【详解】(1)依题意,,
解得.
(2)所有受灾村民经济损失的平均值为3360(元).
(3)由(1)得经济损失在和在的人数比例为,
由分层抽样知,经济损失在的村民抽取人数为人.
18.(1)甲乙平均数分别为7,7,甲乙方差分别为,4
(2)可以认为青少年消费者对甲、乙两个品牌零食集合店的满意度有明显差异
【分析】(1)根据样本平均数、方差的概念及公式可得.
(2)根据题意以及第(1)问的所得数据进行运算判断即可.
【详解】(1)由题意可得:
,
,
,
.
(2)由(1)可得,,
所以,
所以可以认为青少年消费者对甲、乙两个品牌零食集合店的满意度有明显差异.
19.(1)系列,系列
(2)系列平均数,方差,系列平均数,方差,推广系列种植更合适
【分析】(1)将两个系列的数从小到大排列后,根据中位数的定义求解即可;
(2)根据平均数和方差的定义求解即可,再根据方差的大小即可决定要推广的系列.
【详解】(1)解:系列的打分结果从小到大排列为76,79,81,84,86,86,88,92,93,95,
所以系列综合打分的中位数为.
系列的打分结果从小到大排列为75,80,80,83,85,87,90,92,93,95,
所以系列综合打分的中位数为.
(2)解:系列综合打分的平均数,
方差.
系列综合打分的平均数,
方差.
因为两个系列综合打分的中位数相等,平均数相等,方差满足,
所以推广系列种植更合适.
20.答案见解析
【分析】由平均数公式、方程公式可以分别依次求得甲和乙的平均数以及公差,从两个方面比较即可求解.
【详解】甲组成绩的平均数,
乙组成绩的平均数.
甲组数据的方差
,
乙组数据的方差.
选甲组理由:甲、乙两组平均数相差不大,但,甲组成绩波动小.
选乙组理由:,在比赛中,高分团队获胜的概率大.
21.(1)60人
(2)176.25
【分析】(1)根据频率和为1列出方程,可得,进而结合频率公式进行求解即可;
(2)先求出,和,的人数占比,可得该校100名生学身高的分位数落在,,进而列出方程即可求解;
【详解】(1)由频率分布直方图可知,解得,
身高在及以上的学生人数(人;
(2),的人数占比为,,的人数占比为,
所以该校100名生学身高的分位数落在,,
设该校100名生学身高的分位数为,
则,解得,
故该校100名生学身高的分位数为176.25;
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某同学一学期七次模拟考试数学成绩(满分150分)依次为88,98,112,106,122,118,110,则这名同学七次数学成绩的分位数为( )
A.110 B.112 C.115 D.118
2.研究人员测量了某种药物服用8小时后在人体血液中所占的百分比,并将所得数据统计如下图所示,据此可以估计,这种药物服用8小时后在人体血液中所占百分比的中位数为( )
A.6 B.5.5 C.5.2 D.6.5
3.2023年10月4日,在杭州亚运会跳水男子10米台决赛中,中国选手杨昊夺得金牌.中国跳水队包揽杭州亚运会跳水项目全部10枚金牌.跳水比赛的评分规则如下,7位裁判同时给分,去掉两个最高分,去掉两个最低分,剩下的3个分数求和再乘以难度系数,就是该选手本轮的得分,下表就是杨昊比赛中的第一轮得分表,则( )
1号 裁判 2号 裁判 3号 裁判 4号 裁判 5号 裁判 6号 裁判 7号 裁判 难度 系数 本轮 得分
a 9.5 9.0 10.0 9.5 10.0 10.0 3.2 92.80
A.这7个数据的众数只能是10.0
B.这7个数据的中位数只能是9.0
C.a可能是10.0
D.a可能是9.5
4.某机构统计了中国2018—2022年全部工业增加值(单位:万亿元)及增长率数据如图所示,则下列结论错误的是( )
A.2018—2022年中国的全部工业增加值逐年增加
B.2018—2022年中国全部工业增加值的增长率的极差为
C.与上一年相比,2022年中国增加的全部工业增加值是2019年增加的全部工业增加值的2倍
D.2018年中国全部工业增加值的增长率比2018—2022年中国全部工业增加值的增长率的最小值高
5.某机构统计的我国2018-2022年工业增加值及其增长率数据如图所示,则下列结论错误的是( )
2018-2022年工业增加值及其增长率
A.2018-2022年我国的工业增加值逐年增加
B.2018-2022年我国工业增加值的增长率的极差为
C.我国2022年比上一年增加的工业增加值是2019年比上一年增加的工业增加值的2倍
D.我国2018年工业增加值的增长率比2018-2022年工业增加值的最低增长率高
6.某10人的射击小组,在一次射击训练中射击成绩数据如下表,则这组数据的中位数为( )
成绩(单位:环) 6 7 8 9 10
人数 1 2 2 4 1
A.2 B.8 C.8.2 D.8.5
7.如图是我国2017~2022年人用疫苗进出口均价,下列结论不正确的是( )
A.疫苗进口均价最低约为2100美元/千克
B.疫苗出口均价的极差小于3700美元/千克
C.疫苗进口均价的中位数大于2750美元/千克
D.疫苗出口均价的方差大于疫苗进口均价的方差
8.已知一组样本数据分别为,若这组数据的平均数为4,则数据,的方差为( )
A. B.8 C.16 D.24
二、多选题
9.已知第一组样本数据的极差为,中位数为,平均数为,标准差为;第二组样本数据的极差为,中位数为,平均数为,标准差为.若满足,则( )
A. B.
C. D.
10.在去年某校高二年级“校长杯”足球比赛中,甲乙两班每场比赛平均进球数 失球数及所有场次比赛进球个数 失球个数的标准差如下表:
进球个数平均数 失球个数平均数 进球个数标准差 失球个数标准差
甲班 2.3 1.5 0.5 1.1
乙班 1.4 2.1 1.2 0.4
下列说法正确的是( )
A.甲班在防守中比乙班稳定
B.乙班总体实力优于甲班
C.乙班很少不失球
D.乙班在进攻中有时表现很好有时表现较差
11.某同学5次考试中数学、物理成绩如图所示,则( )
A.5次物理成绩的第60百分位数是81 B.5次数学成绩的极差大于物理成绩的极差
C.5次物理成绩的标准差小于3 D.5次数学成绩的平均数大于110
12.为深入推进党史学习教育活动,某校开展了“学史明鉴、牢记使命”知识竞赛活动,从1200名参赛的学生中随机选取100人的成绩作为样本(满分100分,60分及以上为及格,得分均在),按,,,,得到如图所示的频率分布直方图,则下列说法正确的是( )
A.
B.1200名参赛的学生中约有60人不及格
C.选取100人的成绩中,成绩落在的人数是成绩落在的人数的
D.以频率估计概率,从1200名参赛的学生中随机抽取1人,则该学生成绩不低于90分的概率为0.1
三、填空题
13.设实数x,,满足1,3,4,x,y,的平均数与50%分位数相等,则数据x,y,的方差为 .
14.某厂家为了保证防寒服的质量,从生产的保暖絮片中随机抽取多组,得到每组纤维长度(单位:)的均值,并制成如下所示的频率分布直方图,由此估计其纤维长度均值的分位数是 .
15.某班成立了两个数学兴趣小组,组人,组人,经过一周的补习后进行了一次测试,在该测试中,组的平均成绩为分,方差为,组的平均成绩为分,方差为.则在这次测试中全班学生方差为 .
16.已知统计某校1 000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数a的值是 .
四、解答题
17.2023年7月底,受台风杜苏芮影响,京津冀多地出现了特大暴雨,给当地群众的生命和财产造成了重大损失.某村为了了解该村受灾村民的经济损失情况,以便制定合理的帮扶方案,抽调人员进行调查并将该村所有受灾村民的经济损失情况统计如下图所示.
(1)求的值;
(2)求该村所有受灾村民的经济损失的平均值;
(3)现按照分层随机抽样的方法从经济损失在的村民中随机抽取8人,则经济损失在的村民有多少人?
18.随着人们生活水平的提高,对零食的需求也在增加,特别是在年轻人群中,零食已经成为他们日常消费的一部分,新兴的消费群体和消费观念为零食集合店的发展提供了巨大的机会和包容性某公司为了了解青少年消费者对甲、乙两个品牌零食集合店的满意程度,统计了10名青少年消费者对这两个品牌零食集合店的打分(满分10分),结果如下:
甲品牌零食集合店 6 10 7 9 6 5 6 8 8 5
乙品牌零食集合店 5 9 5 4 5 7 10 9 8 8
(1)求样本平均数和方差;
(2)判断青少年消费者对甲、乙两个品牌零食集合店的满意度是否有明显差异(若,则认为青少年消费者对甲、乙两个品牌零食集合店的满意度无明显差异,否则认为有明显差异).
19.某杨梅种植户从购买客户中随机抽取20位客户做质量随访调查,其中购买系列(大棚种植)的10位,购买系列(自然种植)的10位,从杨梅的大小、口感、水分、甜度进行综合打分(满分100分),打分结果记录如下:
系列(大棚种植):84 81 79 76 95 88 93 86 86 92
系列(自然种植):92 95 80 75 83 87 90 80 85 93
(1)分别写出这两个系列综合打分的中位数.
(2)分别求出这两个系列综合打分的平均数与方差,通过上述数据结果进行分析,你认为推广哪种系列种植更合适?
20.某高校共有“机器人”兴趣团队20个,将这20个团队分为甲 乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲 乙两组的成绩如下(单位:分):
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
学校计划从甲、乙两组中选一组参加机器人大赛,从统计学角度分析,若最终选择甲组,理由是什么?若最终选择乙组,理由是什么?
21.随机抽取100名男学生,测得他们的身高(单位:cm),按照区间,,,,分组,得到样本身高的频率分布直方图如图所示
(1)求这100名男学生身高在170cm及以上的学生人数;
(2)估计该校100名学生身高的75%分位数.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】将某同学一学期七次模拟考试数学成绩从低到高排列,根据百分位数的概念,即可求得答案.
【详解】将某同学一学期七次模拟考试数学成绩从低到高排列依次为88,98,106,110,112,118,122,
由于,故这名同学七次数学成绩的分位数为第6个数,即118,
故选:D
2.A
【分析】根据频率分布直方图的特征求出a,结合中位数的定义即可求解.
【详解】依题意,,解得,
则前三块小矩形的面积分别为,,,
所以中位数位于组内,则所求中位数为.
故选:A.
3.D
【分析】根据评分规则,结合众数、中位数的定义进行求解即可.
【详解】当时,由题意可知:,符合题意,此时众数为10或(此时),中位数为9.5,因此选项AB不正确,D正确;
当时,由题意可知:,舍去,因此选项C不正确,
故选:D
4.C
【分析】根据统计图表中的数据,结合每个选项,进行逐一分析,即可判断和选择.
【详解】对A:由条形图知,2018—2022年中国的全部工业增加值逐年增加,故A正确;
对B:由折线图知,2018—2022年中国全部工业增加值的增长率的极差为,故B正确;
对C:由条形图知,与上一年相比,2022年中国增加的全部工业增加值为,
2019年增加的全部工业增加值为,不是2倍关系,故C错误;
对D:由条形图知,2018年中国全部工业增加值的增长率为,
2018—2022年中国全部工业增加值的增长率的最小值为,,故D正确.
故选:C.
5.C
【分析】根据条形图,结合统计相关知识逐项分析判断.
【详解】对于A:由条形图知,2018-2022年我国的工业增加值逐年增加,故A正确;
对于B:由折线图知,2018-2022年我国工业增加值的增长率的极差为,故B正确;
对于C:由条形图知,我国2022年比上一年增加的工业增加值为(万亿元),
2019年比上一年增加的工业增加值为(万亿元),不是2倍关系,故C错误;
对于D:由条形图知,我国2018年工业增加值的增长率为,2018-2022年工业增加值的最低增长率为,
且,故D正确.
故选:C.
6.D
【分析】利用中位数的定义即可得解.
【详解】将射击成绩由小到大排列:,
第个数分别为,因而中位数为.
故选:D.
7.C
【分析】根据图表观察可确定ABD选项,由中位数的定义确定中位数为2019年、2020年的疫苗进口均价的平均数,观察范围即可确定.
【详解】由题图易知选项A,B正确;
对于选项C,疫苗进口均价的中位数是2020年与2021年疫苗进口均价的平均数,2020年的疫苗进口均价小于2500美元/千克,2021年的疫苗进口均价小于3000美元/千克,因此中位数小于2750美元/千克,故选项C不正确;
对于选项D,由题图易知疫苗出口均价波动幅度比疫苗进口均价波动幅度大,所以疫苗出口均价的方差大于疫苗进口均价的方差,故选项D正确.
故选:C.
8.D
【分析】先求出,再结合方差公式可得正确选项.
【详解】由题设有,故,
故,
故数据,的方差为:
,
故选:D.
9.BC
【分析】利用极差的定义可判断A选项;利用中位数的定义可判断B选项;利用平均数公式可判断C选项;利用方差公式可判断D选项.
【详解】解:因为,
对于A,设在数据中最大,最小,则,
则在数据中最大,最小,则,故A错误;
对于B,因为样本数据的中位数为,
当为偶数时,,
又因为,
所以样本数据的中位数为,
当为奇数时,,
又因为,
所以样本数据的中位数为,
所以样本数据的中位数为,故B正确;
对于C,因为样本数据的平均数为 ,
即 ,
所以样本数据的平均数为
,故C正确;
对于D,因为样本数据的标准差为,
样本数据的标准差为 ,
则,
,
,
所以,故D错误.
故选:BC.
10.CD
【分析】由平均数及标准差的大小关系逐一判断各选项.
【详解】由失球个数的标准差可得A错误;
由进球个数和失球个数的平均数可得B错误;
由失球个数的标准差可知C正确;
由进球个数的标准差可知D正确.
故选:CD
11.BD
【分析】根据百分位数,极差,标准差,平均数的计算公式依次得出答案.
【详解】由题知,5次数学成绩从低到高依次排列为:96、101、108、120、128,
5次物理成绩从低到高依次排列为:78、80、81、85、86.
对于A选项,因为,所以5次物理成绩的第60百分位数为,故A选项错误;
对于B选项,5次数学成绩的极差为,5次物理成绩的极差为,数学成绩的极差大于物理成绩的极差,故B选项正确;
对于C选项,5次物理成绩的平均数为,
标准差为,
故C选项错误;
对于D选项,5次数学成绩的平均数为,
平均数大于110,故D选项正确.
故选:BD.
12.BCD
【分析】对于A,利用各小矩形的面积之和为1求解即可;对于B,根据频率分布直方图得到分数小于60的频率,从而求得1200名参赛的学生中不及格的人数;对于C,分别计算出成绩落在的人数和成绩落在的人数,即可判断;对于D,根据频率分布直方图得学生成绩不低于90分的频率,从而得到答案.
【详解】对于A,由,得,故A错误;
对于B,1200名参赛的学生中不及格的人数为,故B正确;
对于C,选取100人的成绩中,成绩落在的人数为,成绩落在的人数为,则成绩落在的人数是成绩落在的人数的,故C正确;
对于D,以频率估计概率,从1200名参赛的学生中随机抽取1人,则该学生成绩不低于90分的概率为,故D正确.
故选:BCD.
13./
【分析】利用平均数与分位数相等,得,代入数据中得方差.
【详解】根据题意,数据的平均数为,
数据的分位数为,
∴ ,即,代入数据,
即为,此组数据的平均数为,
∴ 数据的方差为.
故答案:
14.36
【分析】计算前6个以及前面7个矩形面积之和,确定纤维长度均值的分位数位于第7组内,根据分位数的含义,列式计算,即得答案.
【详解】由频率分布直方图可得从左到右前6个矩形面积之和为:,
前7个矩形面积之和为,
故纤维长度均值的分位数位于第7组内,
设纤维长度均值的分位数为x,则,
解得,
即估计其纤维长度均值的分位数是36,
故答案为:36
15.
【分析】利用各层方差与总体方差之间的关系式可求全班学生方差.
【详解】依题意,,,,
∴(分),
∴全班学生的平均成绩为分.
全班学生成绩的方差为
故答案为:
16.0.020
【详解】
由频率分布直方图的性质,得10(0.005+0.015+a+0.035+0.015+0.010)=1,解得a=0.020.
17.(1)
(2)3360(元)
(3)6人
【分析】(1)由频率分布直方图中各矩形的面积之和为1列方程即可求解;
(2)由频率分布直方图中的平均数计算公式直接运算即可求解;
(3)首先算出经济损失在和在的人数比例,根据分层抽样的抽取方法直接计算即可求解.
【详解】(1)依题意,,
解得.
(2)所有受灾村民经济损失的平均值为3360(元).
(3)由(1)得经济损失在和在的人数比例为,
由分层抽样知,经济损失在的村民抽取人数为人.
18.(1)甲乙平均数分别为7,7,甲乙方差分别为,4
(2)可以认为青少年消费者对甲、乙两个品牌零食集合店的满意度有明显差异
【分析】(1)根据样本平均数、方差的概念及公式可得.
(2)根据题意以及第(1)问的所得数据进行运算判断即可.
【详解】(1)由题意可得:
,
,
,
.
(2)由(1)可得,,
所以,
所以可以认为青少年消费者对甲、乙两个品牌零食集合店的满意度有明显差异.
19.(1)系列,系列
(2)系列平均数,方差,系列平均数,方差,推广系列种植更合适
【分析】(1)将两个系列的数从小到大排列后,根据中位数的定义求解即可;
(2)根据平均数和方差的定义求解即可,再根据方差的大小即可决定要推广的系列.
【详解】(1)解:系列的打分结果从小到大排列为76,79,81,84,86,86,88,92,93,95,
所以系列综合打分的中位数为.
系列的打分结果从小到大排列为75,80,80,83,85,87,90,92,93,95,
所以系列综合打分的中位数为.
(2)解:系列综合打分的平均数,
方差.
系列综合打分的平均数,
方差.
因为两个系列综合打分的中位数相等,平均数相等,方差满足,
所以推广系列种植更合适.
20.答案见解析
【分析】由平均数公式、方程公式可以分别依次求得甲和乙的平均数以及公差,从两个方面比较即可求解.
【详解】甲组成绩的平均数,
乙组成绩的平均数.
甲组数据的方差
,
乙组数据的方差.
选甲组理由:甲、乙两组平均数相差不大,但,甲组成绩波动小.
选乙组理由:,在比赛中,高分团队获胜的概率大.
21.(1)60人
(2)176.25
【分析】(1)根据频率和为1列出方程,可得,进而结合频率公式进行求解即可;
(2)先求出,和,的人数占比,可得该校100名生学身高的分位数落在,,进而列出方程即可求解;
【详解】(1)由频率分布直方图可知,解得,
身高在及以上的学生人数(人;
(2),的人数占比为,,的人数占比为,
所以该校100名生学身高的分位数落在,,
设该校100名生学身高的分位数为,
则,解得,
故该校100名生学身高的分位数为176.25;
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
