2023—2024学年人教版数学八年级下册第十九章 一次函数 单元测试(含答案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级下册第十九章 一次函数 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 397.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 16:15:50 | ||
图片预览


文档简介
第十九章一次函数(单元测试)2023-2024学年八年级下册数学人教版
一、单选题(共10小题,满分40分)
1.若是一次函数图象上的两点,则( )
A. B. C. D.
2.若的函数值随着的增大而增大,则的值可能是( )
A.0 B.1 C.-3 D.-2
3.“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们离家的距离(千米)与汽车行驶时间(小时)之间的函数图像,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A.2小时 B.小时 C.小时 D.小时
4.下列问题中,变量y与x成一次函数关系的是( )
A.长铁丝折成长为,宽为的长方形
B.斜边长为的直角三角形的直角边和
C.圆的面积与它的半径
D.路程一定时,时间和速度的关系
5.已知正比例函数y=(2m-1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m< B.m> C.m<2 D.m>0
6.函数y1=|x|,.当y1>y2时,x的范围是( )
A. B. C.或 D.
7.弹簧挂上物体后会伸长(在允许挂物重量范围内),测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下表的关系:下列说法不正确的是( )
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
A.弹簧不挂重物时的长度为10cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为14cm
8.下列关于一次函数的说法中,错误的是( )
A.其图像经过第一、二、四象限
B.其图像与x轴的交点坐标为(﹣1,0)
C.当时,
D.y随x的增大而减小
9.一次函数与的图象如图所示,下列说法:①对于函数来说,y随x的增大而增大.②函数不经过第二象限.③不等式的解集是. ④,其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
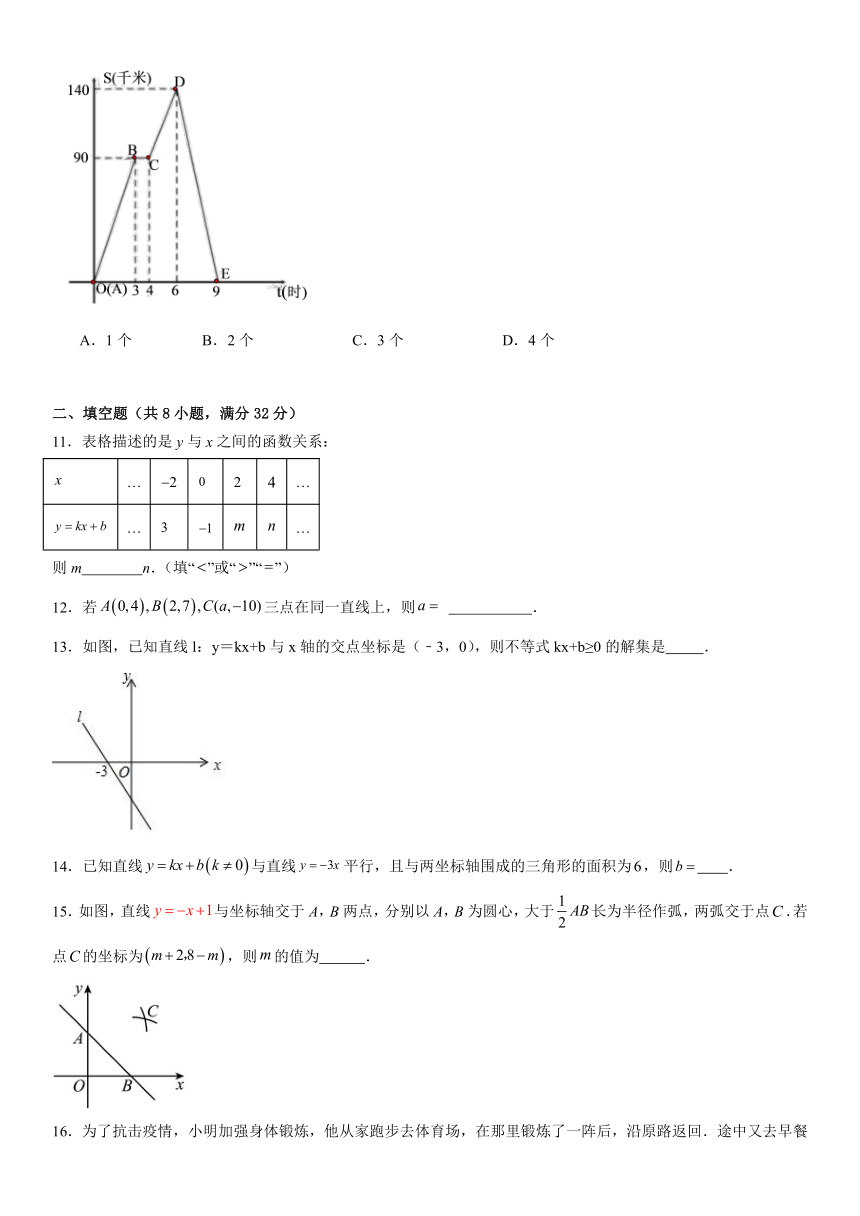
10.如图所示的图象(折线)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离(千米)与行驶时间(时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题,满分32分)
11.表格描述的是y与x之间的函数关系:
… …
… …
则m n.(填“”或“”“”)
12.若三点在同一直线上,则 .
13.如图,已知直线l:y=kx+b与x轴的交点坐标是(﹣3,0),则不等式kx+b≥0的解集是 .
14.已知直线与直线平行,且与两坐标轴围成的三角形的面积为,则 .
15.如图,直线与坐标轴交于A,B两点,分别以A,B为圆心,大于长为半径作弧,两弧交于点.若点的坐标为,则的值为 .
16.为了抗击疫情,小明加强身体锻炼,他从家跑步去体育场,在那里锻炼了一阵后,沿原路返回.途中又去早餐店吃早餐,然后散步走回家,如图,其中x表示时间,y表示小明离家的距离,根据图象提供的信息,有以下四个说法:①体育场离小明家2.5km;②小明在体育场锻炼了15min;③体育场离早餐店1km;④小明从早餐店回家的平均速度是km/h.其中说法正确的有 .
17.某种报纸的价格是每份0.4元,买x份报纸的总价为y元,填写下表.
份数/份 1 2 3 4 …
价钱/元 …
在这个问题中, 是常量; 是变量.
18.一次函数(、为常数,)中的与的部分对应值如下表:
下列结论中一定正确的是 (填序号即可).
①当时,;②当的值随值的增大而增大时,;
③当时,或;④当时,直线与轴相交于点,则.
三、解答题(共6小题,每题8分,满分48分)
19.根据心理学家研究发现,学生对一个新概念的接受能力y与提出概念所用的时间x(分钟)乙间的大水如下数线.
提出概念所用时间 2 5 7 10 12 13 14 17 20
对概念的接受能力 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)根据表格中的数据,提出概念所用时间是多少分钟时,学生的接受能力最强?
(2)学生对一个新概念的接受能力从什么时间开始逐渐减弱?
20.父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,写出t与h的关系式;
(2)你能计算出距离地面8千米的高空温度是多少吗?
21.请根据学习“一次函数”时积累的经验和方法研究函数的图象和性质,并解决问题.
(1)填空:
①当时,______;
②当时,______;
③当时,______;
(2)在平面直角坐标系中作出函数的图象;
(3)观察函数图象,写出关于这个函数的两条结论;
(4)进一步探究函数图象发现:
①函数图象与轴有______个交点;
②方程有______个解;
③若关于的方程无解,则的取值范围是______.
22.直线y=kx+b与直线y=5﹣4x平行,且与直线y=﹣3(x﹣6)相交,交点在y轴上,求直线y=kx+b对应的函数解析式.
23.已知与成正比例,且当时,.
(1)写出与之间的函数表达式;
(2)当时,求的值;
(3)若y的取值范围为,求的取值范围.
24.如图,一次函数y=x+3的图象分别与y轴,x轴交于点A,B,点P从点B出发,沿射线BA以每秒1个单位的速度运动,设点P的运动时间为t秒.
(1)点P在运动过程中,若某一时刻,△OPA的面积为3,求此时P的坐标;
(2)在整个运动过程中,当t为何值时,△AOP为等腰三角形?请直接写出t的值.
试卷第1页,共3页
参考答案:
1.D
2.B
3.C
4.A
5.A
6.C
7.D
8.B
9.B
10.A
11.
12.
13.x≤﹣3
14.或
15.3
16.①②③
17. 0.4;0.8;1.2;1.6;0.4 x,y
18.①②③
19.(1)13分钟
(2)第13分钟
20.(1);
(2).
21.(1);;
(2)略
(3)①函数图象关于轴对称;②当时,有最小值.(答案不唯一)
(4)2;1;
22..
23.(1) ;(2) ;(3) .
24.(1)点P的坐标为(﹣2,)或(2,);(2)当t的值为2、8、和时,△AOP为等腰三角形.
答案第1页,共2页
一、单选题(共10小题,满分40分)
1.若是一次函数图象上的两点,则( )
A. B. C. D.
2.若的函数值随着的增大而增大,则的值可能是( )
A.0 B.1 C.-3 D.-2
3.“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们离家的距离(千米)与汽车行驶时间(小时)之间的函数图像,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A.2小时 B.小时 C.小时 D.小时
4.下列问题中,变量y与x成一次函数关系的是( )
A.长铁丝折成长为,宽为的长方形
B.斜边长为的直角三角形的直角边和
C.圆的面积与它的半径
D.路程一定时,时间和速度的关系
5.已知正比例函数y=(2m-1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m< B.m> C.m<2 D.m>0
6.函数y1=|x|,.当y1>y2时,x的范围是( )
A. B. C.或 D.
7.弹簧挂上物体后会伸长(在允许挂物重量范围内),测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下表的关系:下列说法不正确的是( )
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
A.弹簧不挂重物时的长度为10cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为14cm
8.下列关于一次函数的说法中,错误的是( )
A.其图像经过第一、二、四象限
B.其图像与x轴的交点坐标为(﹣1,0)
C.当时,
D.y随x的增大而减小
9.一次函数与的图象如图所示,下列说法:①对于函数来说,y随x的增大而增大.②函数不经过第二象限.③不等式的解集是. ④,其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
10.如图所示的图象(折线)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离(千米)与行驶时间(时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题,满分32分)
11.表格描述的是y与x之间的函数关系:
… …
… …
则m n.(填“”或“”“”)
12.若三点在同一直线上,则 .
13.如图,已知直线l:y=kx+b与x轴的交点坐标是(﹣3,0),则不等式kx+b≥0的解集是 .
14.已知直线与直线平行,且与两坐标轴围成的三角形的面积为,则 .
15.如图,直线与坐标轴交于A,B两点,分别以A,B为圆心,大于长为半径作弧,两弧交于点.若点的坐标为,则的值为 .
16.为了抗击疫情,小明加强身体锻炼,他从家跑步去体育场,在那里锻炼了一阵后,沿原路返回.途中又去早餐店吃早餐,然后散步走回家,如图,其中x表示时间,y表示小明离家的距离,根据图象提供的信息,有以下四个说法:①体育场离小明家2.5km;②小明在体育场锻炼了15min;③体育场离早餐店1km;④小明从早餐店回家的平均速度是km/h.其中说法正确的有 .
17.某种报纸的价格是每份0.4元,买x份报纸的总价为y元,填写下表.
份数/份 1 2 3 4 …
价钱/元 …
在这个问题中, 是常量; 是变量.
18.一次函数(、为常数,)中的与的部分对应值如下表:
下列结论中一定正确的是 (填序号即可).
①当时,;②当的值随值的增大而增大时,;
③当时,或;④当时,直线与轴相交于点,则.
三、解答题(共6小题,每题8分,满分48分)
19.根据心理学家研究发现,学生对一个新概念的接受能力y与提出概念所用的时间x(分钟)乙间的大水如下数线.
提出概念所用时间 2 5 7 10 12 13 14 17 20
对概念的接受能力 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)根据表格中的数据,提出概念所用时间是多少分钟时,学生的接受能力最强?
(2)学生对一个新概念的接受能力从什么时间开始逐渐减弱?
20.父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,写出t与h的关系式;
(2)你能计算出距离地面8千米的高空温度是多少吗?
21.请根据学习“一次函数”时积累的经验和方法研究函数的图象和性质,并解决问题.
(1)填空:
①当时,______;
②当时,______;
③当时,______;
(2)在平面直角坐标系中作出函数的图象;
(3)观察函数图象,写出关于这个函数的两条结论;
(4)进一步探究函数图象发现:
①函数图象与轴有______个交点;
②方程有______个解;
③若关于的方程无解,则的取值范围是______.
22.直线y=kx+b与直线y=5﹣4x平行,且与直线y=﹣3(x﹣6)相交,交点在y轴上,求直线y=kx+b对应的函数解析式.
23.已知与成正比例,且当时,.
(1)写出与之间的函数表达式;
(2)当时,求的值;
(3)若y的取值范围为,求的取值范围.
24.如图,一次函数y=x+3的图象分别与y轴,x轴交于点A,B,点P从点B出发,沿射线BA以每秒1个单位的速度运动,设点P的运动时间为t秒.
(1)点P在运动过程中,若某一时刻,△OPA的面积为3,求此时P的坐标;
(2)在整个运动过程中,当t为何值时,△AOP为等腰三角形?请直接写出t的值.
试卷第1页,共3页
参考答案:
1.D
2.B
3.C
4.A
5.A
6.C
7.D
8.B
9.B
10.A
11.
12.
13.x≤﹣3
14.或
15.3
16.①②③
17. 0.4;0.8;1.2;1.6;0.4 x,y
18.①②③
19.(1)13分钟
(2)第13分钟
20.(1);
(2).
21.(1);;
(2)略
(3)①函数图象关于轴对称;②当时,有最小值.(答案不唯一)
(4)2;1;
22..
23.(1) ;(2) ;(3) .
24.(1)点P的坐标为(﹣2,)或(2,);(2)当t的值为2、8、和时,△AOP为等腰三角形.
答案第1页,共2页
