15.2随机事件的概率 同步练习(含解析)2023——2024学年苏教版(2019)高中数学必修第二册
文档属性
| 名称 | 15.2随机事件的概率 同步练习(含解析)2023——2024学年苏教版(2019)高中数学必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 16:33:39 | ||
图片预览




文档简介
15.2 随机事件的概率 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知6件产品中有2件次品,从中随机抽取2件,其中恰好有1件正品的概率为( )
A. B. C. D.
2.随着国潮的兴起,消费者对汉服的接受度日渐提高,数据显示,目前中国大众穿汉服的场景主要有汉服活动、艺术拍摄、传统节日、旅游观光、舞台表演、婚庆典礼6类,某自媒体博主准备从这6类场景中选2类拍摄中国大众穿汉服的照片,则汉服活动、旅游观光这2类场景至少有1类场景被选中的概率为( )
A. B. C. D.
3.“142857”这一串数字被称为走马灯数,是世界上著名的几个数之一,当142857与1至6中任意一个数字相乘,乘积中仍然是1,4,2,8,5,7这6个数字轮流出现.若从1,4,2,8,5,7这6个数字中任选2个数字组成无重复数字的两位数,从这些两位数中随机选取1个,这个两位数大于72的概率为( )
A. B. C. D.
4.下列事件中,随机事件的个数是( )个.
①某人购买福利彩票一注,中奖万元;②三角形的内角和为;
③地球上,没有空气和水,人类可以生存下去;④同时抛掷两枚硬币一次,都出现正面向上.
A. B. C. D.
5.近几年随着技术的发展,虚拟人的智能化水平得到极大的提升,虚拟主播逐步走向商用,下图为2014~2022年中国虚拟主播企业注册增加数(较上一年增加的数量)条形图,根据该图,下列说法错误的是( )
A.2014~2022年中国虚拟主播企业注册数量逐年增加
B.2014~2022年中国虚拟主播企业注册年增加数的中位数为410
C.2014~2022年中国虚拟主播企业注册年增加数的极差为915
D.从2018~2022年企业注办增加数字中任取2个数字,这两个数字的平均数不大于300的概率为
6.有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为( )
A. B. C. D.
7.某不透明的袋中有3个红球,2个白球,它们除颜色不同,质地和大小都完全相同.甲、乙两同学先后从中各取一个球,先取的球不放回,则他们取到不同颜色球的概率为( )
A. B. C. D.
8.某学校开展关于“饮食民俗”的选修课程,课程内容分为日常食俗,节日食俗,祭祀食俗,待客食俗,特殊食俗,快速食俗6个模块,甲、乙两名学生准备从中各选择2个模块学习,则甲、乙选修的模块中至少有1个模块相同的概率为( )
A. B. C. D.
二、多选题
9.甲、乙两人做游戏,下列游戏中公平的是( )
A.抛一枚骰子,向上的点数为奇数则甲胜,向上的点数为偶数则乙胜
B.同时抛掷两枚硬币,恰有一枚正面向上则甲胜,两枚都是正面向上则乙胜
C.从一副不含大、小王的扑克牌中抽一张,扑克牌是红色则甲胜,是黑色则乙胜
D.甲、乙两人各写一个数字,若是同奇或同偶则甲胜,否则乙胜
10.如图,从1开始出发,一次移动是指:从某一格开始只能移动到邻近的一格,并且总是向右或右上或右下移动,而一条移动路线由若干次移动构成,如从1移动到9,就是一条移动路线.从1移动到数字的不同路线条数记为,从1移动到9的事件中,跳过数字的概率记为,则下列结论正确的是( )
A. B.
C. D.
11.下列说法正确的是( )
A.一名篮球运动员,号称投篮“百发百中”,则他投篮一次,命中为必然事件
B.随机事件发生的可能性越大,它发生的概率越接近1
C.投掷两枚均匀的骰子,观察出现的点数和,点数和为2是一个样本点
D.试验“连续投掷一枚均匀的骰子直到出现3点停止,观察投掷的次数”的样本空间为
12.同时掷红、蓝两枚质地均匀的正四面体骰子,骰子的面上标有1、2、3、4,记录骰子朝下的面上的点数,事件表示“两枚骰子的点数之和为”,事件表示“红色骰子的点数是偶数”,事件表示“两枚骰子的点数相同”,事件表示“至少一枚骰子的点数是偶数”.则下列说法中正确的是( )
A. B.
C. D.
三、填空题
13.将一枚股子连抛两次,记事件为“第一次得到1点”,事件为“两次得到的点数之和为7”,则 .
14.在区域内任取一点,使点落在区域内的概率为 .
15.设是一个随机试验中的两个事件,且,则 .
16.某班成立了,两个数学兴趣小组,组有5名学生,组有10名学生.在某次测验中,组学生的成绩如图所示,组学生的平均成绩为117分,方差为14.若从组学生中随机抽取2人作为兴趣小组组长,则这2个组长的成绩均在120分以上的概率为 ;若将组学生、组学生该次测验的成绩混合在一起,产生一组新的数据,则这组新数据的方差为 .
四、解答题
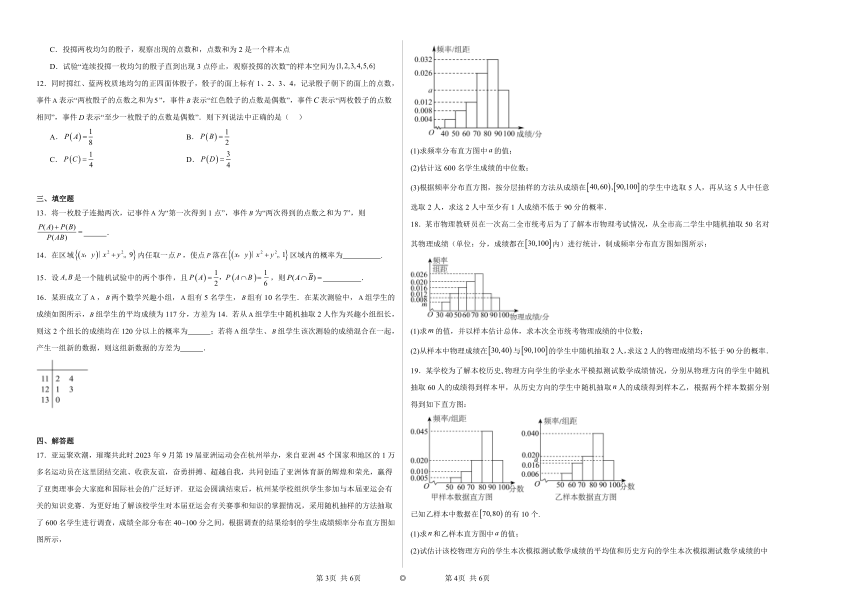
17.亚运聚欢潮,璀璨共此时.2023年9月第19届亚洲运动会在杭州举办,来自亚洲45个国家和地区的1万多名运动员在这里团结交流、收获友谊,奋勇拼搏、超越自我,共同创造了亚洲体育新的辉煌和荣光,赢得了亚奥理事会大家庭和国际社会的广泛好评.亚运会圆满结束后,杭州某学校组织学生参加与本届亚运会有关的知识竞赛.为更好地了解该校学生对本届亚运会有关赛事和知识的掌握情况,采用随机抽样的方法抽取了600名学生进行调查,成绩全部分布在40~100分之间,根据调查的结果绘制的学生成绩频率分布直方图如图所示,
(1)求频率分布直方图中的值;
(2)估计这600名学生成绩的中位数;
(3)根据频率分布直方图,按分层抽样的方法从成绩在的学生中选取5人,再从这5人中任意选取2人,求这2人中至少有1人成绩不低于90分的概率.
18.某市物理教研员在一次高二全市统考后为了了解本市物理考试情况,从全市高二学生中随机抽取50名对其物理成绩(单位:分,成绩都在内)进行统计,制成频率分布直方图如图所示:
(1)求的值,并以样本估计总体,求本次全市统考物理成绩的中位数;
(2)从样本中物理成绩在与的学生中随机抽取2人,求这2人的物理成绩均不低于90分的概率.
19.某学校为了解本校历史 物理方向学生的学业水平模拟测试数学成绩情况,分别从物理方向的学生中随机抽取60人的成绩得到样本甲,从历史方向的学生中随机抽取人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:
已知乙样本中数据在的有10个.
(1)求和乙样本直方图中的值;
(2)试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表).
(3)采用分层抽样的方法从甲样本数据中分数在和的学生中抽取6人,并从这6人中任取2人,求这两人分数都在中的概率.
20.某校对2023年高一上学期期末数学考试成绩(单位:分)进行分析,随机抽取100名学生,将分数按照,,,,,分成6组,绘制成如图所示的频率分布直方图:
(1)求频率分布直方图中的值;
(2)估计该校高一上学期期末数学考试成绩的中位数;
(3)为了进一步了解学生对数学学习的情况,在成绩位于和的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在内的概率.
21.Unidentified Flying Object,简称UFO,俗称飞碟,通常被人们看作是外地文明派到地球的使者.为了调查国内网友对UFO的了解情况,资深UFO爱好者李磊,在网上发起了一项“UFO”有奖问答,共有10000名网友参加,李磊随机抽取了1000名(得分都在60~100分之间),将得分分成4组:,,,,并整理得到如下频率分布直方图:
(1)李磊决定根据得分从高到低,对参与活动的的高分网友发放奖品,试估计这次有奖问答的获奖分数线;(保留一位小数)
(2)用分层随机抽样的方法从,两个分数段共抽取出4名网友,再从这4名网友中随机抽取2名依次分享UFO时间供大家交流,求第一个分享的网友得分在的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】列举出所有情况和满足要求的情况,利用古典概型求概率公式求出答案.
【详解】由题意,设4件正品的编号分别为件次品的编号分别为,
则从这6件产品中随机抽取2件的所有情况为,
,共15种.
设恰好有1件正品为事件,
则事件包含的情况有,共8种,
则.
故选:A.
2.C
【分析】列举出从6类场景中选2类场景进行拍摄的所有基本事件,再列举出汉服活动、旅游观光这2类场景至少有1类场景被选中的基本事件,根据古典概型的概率公式,即可求得答案.
【详解】记汉服活动、艺术拍摄、传统节日、旅游观光、舞台表演、婚庆典礼这6类场景分别为A,B,C,D,E,F,
从6类场景中选2类场景进行拍摄的基本事件有
,,,,,,,,,
,,,,,,共15种,
设事件M为“汉服活动、旅游观光这2类场景至少有1类场景被选中”,
则事件M包含的基本事件有,,,,,
,,,,共9种,
故所求概率,
故选:C.
3.C
【分析】用列举法即可求解古典概型概率问题.
【详解】从1,4,2,8,5,7这6个数字中任选2个,
所有不同的情况为:,,,,,,,,,
,,,,,,共15种,
则组成无重复数字的两位数的个数为.
若选取的两位数大于72,
则十位数字只能是7或8,
符合要求的所有的两位数为74,75,78,81,82,84,85,87,共8个,
故所求概率.
故选:C.
4.B
【分析】利用随机事件的定义逐个判断,可得出结论.
【详解】对于事件①,某人购买福利彩票一注,中奖万元,该事件为随机事件;
对于事件②,三角形的内角和为,该事件为必然事件;
对于事件③,地球上,没有空气和水,人类可以生存下去,该事件为不可能事件;
对于事件④,同时抛掷两枚硬币一次,都出现正面向上,该事件为随机事件.
因此,随机事件的个数为.
故选:B.
5.B
【分析】
根据条形统计图判断A、B、C ,利用古典概型的概率公式判断D.
【详解】由每年注册增加数均为正数,可知2014~2022年中国虚拟主播企业注册数量逐年增加,故A正确;
2014~2022年中国虚拟主播企业注册年增加数从小到大排列为:,,,,,,,,,
所以2014~2022年中国虚拟主播企业注册年增加数的中位数为,故B错误;
2014~2022年中国虚拟主播企业注册年增加数的极差为,故C正确;
从,,,,中任取两个数字,结果有种,
所取两个数字平均数不大于的取法有,共种,
所以所求概率,故D正确.
故选:B.
6.A
【分析】
列出所有情况,再根据古典概率计算公式即可.
【详解】
从袋中一次随机摸出2个球,共有6种基本事件,
其中摸出的2个球的编号之和大于4的事件为,四种基本事件数,因此概率为.
故选:A.
7.C
【分析】
列出所有可能,再找出符合要求的情况即可得.
【详解】设这几个球中,红球分别为、、,白球分别为、,
则甲、乙两同学先后取出的两球可能的情况有:
、、、、、、、、、、
、、、、、、、、、、共二十种,
其中取到不同颜色球的情况有:
、、、、、、、、、、、共十二种,
故其概率为.
故选:C.
8.C
【分析】记6个模块分别为,求出总的基本事件数,然后求出甲、乙选择都不同的基本事件数,利用间接法求概率.
【详解】记6个模块分别为,
则甲从中选择2个共有共种不同的选择,
而甲每种的选择中乙与甲都不同有6种,
所以甲、乙各选2个共有种不同选择,而甲、乙选择都不同有种不同选择,
所以甲、乙选修的模块中至少有1个相同的概率.
故选:C.
9.ACD
【分析】
根据古典概型求解概率即可比较求解.
【详解】
A项,P(点数为奇数) P(点数为偶数);
B, 同时抛掷两枚硬币,共有4种情况:正正;正反;反正;正反.
则 P(恰有一枚正面向上),P(两枚都正面向上)=;概率不相等,故B错误,
C项,P(牌色为红) P(牌色为黑) ;
D项,P(同奇或同偶)=P(奇偶不同) .
故选:ACD.
10.ABC
【分析】画出树状图,结合图形及古典概型逐项分析判断.
【详解】画出树状图,结合图形
结合树状图可知:,
对于选项A:可知,故A正确;
对于选项B: 均有,故B正确;
对于选项C:因为,不经过数字5的路线有9条,所以,故C正确;
对于选项D:因为,所以,故D错误;
故选:ABC.
11.BC
【分析】由随机事件以及它的概率范围即可判断AB,由样本点,样本空间的定义即可判断CD.
【详解】对于A,他投篮一次,命中为随机事件,故A错误;
对于B,随机事件发生的可能性越大,它发生的概率越接近1,故B正确;
对于C,点数和为2当且仅当两枚骰子出现的点数都为1,这是有可能的,故C正确;
对于D,试验“连续投掷一枚均匀的骰子直到出现3点停止,观察投掷的次数”的样本空间为,故D错误.
故选:BC.
12.BCD
【分析】根据题意,列举法找到所有可能情况,由古典概型的概率计算公式分别计算.
【详解】设红骰子朝下的面上的点数为m,蓝骰子朝下的面上的点数为n,样本点为,
则样本空间为,则,
事件表示“两枚骰子的点数之和为”,
,
所以,故A错误;
事件表示“红色骰子的点数是偶数”,
所以,故B正确;
事件表示“两枚骰子的点数相同”,
,
所以,故C正确;
事件表示“至少一枚骰子的点数是偶数”,
,
所以,故D正确.
故选:BCD
13.12
【分析】根据列举法,结合古典概型的概率计算公式求解即可.
【详解】由题意得,一枚股子连抛两次的所有可能情况共36种,
事件A的所有可能情况为,共6种,
事件B的所有可能情况为,共6种,
事件AB的所有可能情况为,共1种,
所以,,,
所以.
故答案为:12
14.
【分析】根据集合意义即可求解.
【详解】区域,表示以圆心,半径为3的圆及其内部,
区域,表示以圆心,半径为1的圆,
结合图形可得所求概率.
故答案为:
15.
【分析】由可得答案.
【详解】因为,
所以.
故答案为:.
16. /0.3 /
【分析】根据给定的茎叶图,结合列举法求出古典概率;求出组学生该次测试成绩的平均成绩及方差,再利用分层抽样的方差公式计算即得.
【详解】由茎叶图知,组5名学生的测试成绩分别为,他们分别记为,
从5名学生任抽2人的样本空间,共10个,
成绩均在以上的事件,共3个,
所以这2个组长的成绩均在120分以上的概率为;
组5名学生测试成绩的平均分为,
方差为,而组学生的平均成绩为,方差为,
因此新数据组的平均分,
方差.
故答案为:;
17.(1)
(2)80
(3)
【分析】(1)根据各矩形面积之和为1,列式计算,即可求得a的值;
(2)根据频率分布直方图,结合中位数的求解方法,即可求得答案;
(3)求出内的人数之比,根据分层抽样可求得两组各抽取的人数,列举出从这5人中任意选取2人的所有可能情况,再列举出这2人中至少有1人成绩不低于90分的情况,根据古典概型的概率公式,即可求得答案.
【详解】(1)由频率分布直方图,得,
解得;
(2)由频率分布直方图,得,
,
则估计这600名学生成绩的中位数为80;
(3)由题意得,成绩在的频率为,
成绩在的频率为,频率之比为,
所以按分层抽样的方法从中选取5人,成绩在的学生有2人,分别记为,
成绩在的学生有3人,分别记为,
从这5人中任意选取2人,有,共10种选法,
其中至少有1人成绩不低于90分的选法有,,共9种,
所以这2人中至少有1人成绩不低于90分的概率.
18.(1),中位数为
(2)
【分析】(1)由概率和为1计算的值,由频率分布直方图中位数的计算公式计算中位数.
(2)根据频率分布直方图计算成绩在与的学生人数,列举法分别求出随机抽取2人总的情况数和中抽取2人的情况数,做比即可求出概率.
【详解】(1)由题知,, 解得.
,
,
故设中位数为,则,则,解得,
所以本次全市统考物理成绩的中位数为68分.
(2)由题知,样本中物理成绩在的学生人数为,设为,
物理成绩在的学生人数为,设为,
从这7人中随机抽取2人的所有情况为,,,,共21种不同情况,
记事件为“这2人的物理成绩均不低于90分”,则事件包含的情况有,共6种不同情况,
,所以这2人的物理成绩均不低于90分的概率为.
19.(1);;
(2)平均值81.5,中位数82;
(3)
【分析】(1)根据频率定义即可求出,再根据小矩形面积和为1即可求出值;
(2)根据平均数和中位数定义计算即可;
(3)列出所有情况和满足题意的情况,再利用古典概率公式即可.
【详解】(1)由直方图可知,乙样本中数据在的频率为,
则,解得;
由乙样本数据直方图可知,,
解得;
(2)甲样本数据的平均值估计值为
,
乙样本数据直方图中前3组的频率之和为,
前4组的频率之和为,
所以乙样本数据的中位数在第4组,设中位数为,
,
解得,所以乙样本数据的中位数为82.
(3)由频率分布直方图可知从分数在和的学生中分别抽取2人和4人,
将从分数在中抽取的2名学生分别记为,从分数在中抽取的4名学生分别记为,
则从这6人中随机抽取2人的基本事件有
,共15个,
所抽取的两人分数都在中的基本事件有6个,所以所求概率为.
20.(1)
(2)97.5
(3)
【分析】(1)根据频率分布直方图中各小矩形的面积之和为1计算即可;
(2)根据频率分布直方图和中位数的定义进行计算即可;
(3)根据题意列出样本空间,根据古典概型概率计算公式求解即可.
【详解】(1)由,
可得.
(2)由(1)知样本数据中数学考试成绩90分以下的所占比例为,
110分以下的所占比例为,
因此,中位数一定位于内,由,
可以估计样本数据的中位数约为97.5分,
据此可以估计该校高一上学期期末数学考试成绩的中位数约为97.5分.
(3)由题意分数段的人数为,
分数段的人数为,
用按比例分配的分层随机抽样的方法抽取5名学生,
则需在分数段内抽取2人,分别记为,,
分数段内抽取3人,分别记为,,.
设“从这5名学生中任取2人,至少有1人成绩在)内”为事件,
则样本空间,共包含10个样本点,
而事件包含7个样本点,所以,
故抽取的这2名学生至少有1人成绩在内的概率为.
21.(1);
(2).
【分析】(1)根据给定的频率分布直方图,利用面积法列式计算即得.
(2)求出两段抽取的人数,再利用列举法求出古典概率.
【详解】(1)分数在的频率为0.3,依题意,有奖问答的获奖分数线,
则,解得,
所以这次有奖问答的获奖分数线约为.
(2)分数在的频率分别为,因此抽取的4人中,分数在内的抽1人,记为,
分数在内的抽3人,依次记为,
抽取2人依次分享的试验样本空间,共12个结果,
第一个分享的得分在的事件,共9个结果,
所以第一个分享的网友得分在的概率.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知6件产品中有2件次品,从中随机抽取2件,其中恰好有1件正品的概率为( )
A. B. C. D.
2.随着国潮的兴起,消费者对汉服的接受度日渐提高,数据显示,目前中国大众穿汉服的场景主要有汉服活动、艺术拍摄、传统节日、旅游观光、舞台表演、婚庆典礼6类,某自媒体博主准备从这6类场景中选2类拍摄中国大众穿汉服的照片,则汉服活动、旅游观光这2类场景至少有1类场景被选中的概率为( )
A. B. C. D.
3.“142857”这一串数字被称为走马灯数,是世界上著名的几个数之一,当142857与1至6中任意一个数字相乘,乘积中仍然是1,4,2,8,5,7这6个数字轮流出现.若从1,4,2,8,5,7这6个数字中任选2个数字组成无重复数字的两位数,从这些两位数中随机选取1个,这个两位数大于72的概率为( )
A. B. C. D.
4.下列事件中,随机事件的个数是( )个.
①某人购买福利彩票一注,中奖万元;②三角形的内角和为;
③地球上,没有空气和水,人类可以生存下去;④同时抛掷两枚硬币一次,都出现正面向上.
A. B. C. D.
5.近几年随着技术的发展,虚拟人的智能化水平得到极大的提升,虚拟主播逐步走向商用,下图为2014~2022年中国虚拟主播企业注册增加数(较上一年增加的数量)条形图,根据该图,下列说法错误的是( )
A.2014~2022年中国虚拟主播企业注册数量逐年增加
B.2014~2022年中国虚拟主播企业注册年增加数的中位数为410
C.2014~2022年中国虚拟主播企业注册年增加数的极差为915
D.从2018~2022年企业注办增加数字中任取2个数字,这两个数字的平均数不大于300的概率为
6.有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为( )
A. B. C. D.
7.某不透明的袋中有3个红球,2个白球,它们除颜色不同,质地和大小都完全相同.甲、乙两同学先后从中各取一个球,先取的球不放回,则他们取到不同颜色球的概率为( )
A. B. C. D.
8.某学校开展关于“饮食民俗”的选修课程,课程内容分为日常食俗,节日食俗,祭祀食俗,待客食俗,特殊食俗,快速食俗6个模块,甲、乙两名学生准备从中各选择2个模块学习,则甲、乙选修的模块中至少有1个模块相同的概率为( )
A. B. C. D.
二、多选题
9.甲、乙两人做游戏,下列游戏中公平的是( )
A.抛一枚骰子,向上的点数为奇数则甲胜,向上的点数为偶数则乙胜
B.同时抛掷两枚硬币,恰有一枚正面向上则甲胜,两枚都是正面向上则乙胜
C.从一副不含大、小王的扑克牌中抽一张,扑克牌是红色则甲胜,是黑色则乙胜
D.甲、乙两人各写一个数字,若是同奇或同偶则甲胜,否则乙胜
10.如图,从1开始出发,一次移动是指:从某一格开始只能移动到邻近的一格,并且总是向右或右上或右下移动,而一条移动路线由若干次移动构成,如从1移动到9,就是一条移动路线.从1移动到数字的不同路线条数记为,从1移动到9的事件中,跳过数字的概率记为,则下列结论正确的是( )
A. B.
C. D.
11.下列说法正确的是( )
A.一名篮球运动员,号称投篮“百发百中”,则他投篮一次,命中为必然事件
B.随机事件发生的可能性越大,它发生的概率越接近1
C.投掷两枚均匀的骰子,观察出现的点数和,点数和为2是一个样本点
D.试验“连续投掷一枚均匀的骰子直到出现3点停止,观察投掷的次数”的样本空间为
12.同时掷红、蓝两枚质地均匀的正四面体骰子,骰子的面上标有1、2、3、4,记录骰子朝下的面上的点数,事件表示“两枚骰子的点数之和为”,事件表示“红色骰子的点数是偶数”,事件表示“两枚骰子的点数相同”,事件表示“至少一枚骰子的点数是偶数”.则下列说法中正确的是( )
A. B.
C. D.
三、填空题
13.将一枚股子连抛两次,记事件为“第一次得到1点”,事件为“两次得到的点数之和为7”,则 .
14.在区域内任取一点,使点落在区域内的概率为 .
15.设是一个随机试验中的两个事件,且,则 .
16.某班成立了,两个数学兴趣小组,组有5名学生,组有10名学生.在某次测验中,组学生的成绩如图所示,组学生的平均成绩为117分,方差为14.若从组学生中随机抽取2人作为兴趣小组组长,则这2个组长的成绩均在120分以上的概率为 ;若将组学生、组学生该次测验的成绩混合在一起,产生一组新的数据,则这组新数据的方差为 .
四、解答题
17.亚运聚欢潮,璀璨共此时.2023年9月第19届亚洲运动会在杭州举办,来自亚洲45个国家和地区的1万多名运动员在这里团结交流、收获友谊,奋勇拼搏、超越自我,共同创造了亚洲体育新的辉煌和荣光,赢得了亚奥理事会大家庭和国际社会的广泛好评.亚运会圆满结束后,杭州某学校组织学生参加与本届亚运会有关的知识竞赛.为更好地了解该校学生对本届亚运会有关赛事和知识的掌握情况,采用随机抽样的方法抽取了600名学生进行调查,成绩全部分布在40~100分之间,根据调查的结果绘制的学生成绩频率分布直方图如图所示,
(1)求频率分布直方图中的值;
(2)估计这600名学生成绩的中位数;
(3)根据频率分布直方图,按分层抽样的方法从成绩在的学生中选取5人,再从这5人中任意选取2人,求这2人中至少有1人成绩不低于90分的概率.
18.某市物理教研员在一次高二全市统考后为了了解本市物理考试情况,从全市高二学生中随机抽取50名对其物理成绩(单位:分,成绩都在内)进行统计,制成频率分布直方图如图所示:
(1)求的值,并以样本估计总体,求本次全市统考物理成绩的中位数;
(2)从样本中物理成绩在与的学生中随机抽取2人,求这2人的物理成绩均不低于90分的概率.
19.某学校为了解本校历史 物理方向学生的学业水平模拟测试数学成绩情况,分别从物理方向的学生中随机抽取60人的成绩得到样本甲,从历史方向的学生中随机抽取人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:
已知乙样本中数据在的有10个.
(1)求和乙样本直方图中的值;
(2)试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表).
(3)采用分层抽样的方法从甲样本数据中分数在和的学生中抽取6人,并从这6人中任取2人,求这两人分数都在中的概率.
20.某校对2023年高一上学期期末数学考试成绩(单位:分)进行分析,随机抽取100名学生,将分数按照,,,,,分成6组,绘制成如图所示的频率分布直方图:
(1)求频率分布直方图中的值;
(2)估计该校高一上学期期末数学考试成绩的中位数;
(3)为了进一步了解学生对数学学习的情况,在成绩位于和的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在内的概率.
21.Unidentified Flying Object,简称UFO,俗称飞碟,通常被人们看作是外地文明派到地球的使者.为了调查国内网友对UFO的了解情况,资深UFO爱好者李磊,在网上发起了一项“UFO”有奖问答,共有10000名网友参加,李磊随机抽取了1000名(得分都在60~100分之间),将得分分成4组:,,,,并整理得到如下频率分布直方图:
(1)李磊决定根据得分从高到低,对参与活动的的高分网友发放奖品,试估计这次有奖问答的获奖分数线;(保留一位小数)
(2)用分层随机抽样的方法从,两个分数段共抽取出4名网友,再从这4名网友中随机抽取2名依次分享UFO时间供大家交流,求第一个分享的网友得分在的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】列举出所有情况和满足要求的情况,利用古典概型求概率公式求出答案.
【详解】由题意,设4件正品的编号分别为件次品的编号分别为,
则从这6件产品中随机抽取2件的所有情况为,
,共15种.
设恰好有1件正品为事件,
则事件包含的情况有,共8种,
则.
故选:A.
2.C
【分析】列举出从6类场景中选2类场景进行拍摄的所有基本事件,再列举出汉服活动、旅游观光这2类场景至少有1类场景被选中的基本事件,根据古典概型的概率公式,即可求得答案.
【详解】记汉服活动、艺术拍摄、传统节日、旅游观光、舞台表演、婚庆典礼这6类场景分别为A,B,C,D,E,F,
从6类场景中选2类场景进行拍摄的基本事件有
,,,,,,,,,
,,,,,,共15种,
设事件M为“汉服活动、旅游观光这2类场景至少有1类场景被选中”,
则事件M包含的基本事件有,,,,,
,,,,共9种,
故所求概率,
故选:C.
3.C
【分析】用列举法即可求解古典概型概率问题.
【详解】从1,4,2,8,5,7这6个数字中任选2个,
所有不同的情况为:,,,,,,,,,
,,,,,,共15种,
则组成无重复数字的两位数的个数为.
若选取的两位数大于72,
则十位数字只能是7或8,
符合要求的所有的两位数为74,75,78,81,82,84,85,87,共8个,
故所求概率.
故选:C.
4.B
【分析】利用随机事件的定义逐个判断,可得出结论.
【详解】对于事件①,某人购买福利彩票一注,中奖万元,该事件为随机事件;
对于事件②,三角形的内角和为,该事件为必然事件;
对于事件③,地球上,没有空气和水,人类可以生存下去,该事件为不可能事件;
对于事件④,同时抛掷两枚硬币一次,都出现正面向上,该事件为随机事件.
因此,随机事件的个数为.
故选:B.
5.B
【分析】
根据条形统计图判断A、B、C ,利用古典概型的概率公式判断D.
【详解】由每年注册增加数均为正数,可知2014~2022年中国虚拟主播企业注册数量逐年增加,故A正确;
2014~2022年中国虚拟主播企业注册年增加数从小到大排列为:,,,,,,,,,
所以2014~2022年中国虚拟主播企业注册年增加数的中位数为,故B错误;
2014~2022年中国虚拟主播企业注册年增加数的极差为,故C正确;
从,,,,中任取两个数字,结果有种,
所取两个数字平均数不大于的取法有,共种,
所以所求概率,故D正确.
故选:B.
6.A
【分析】
列出所有情况,再根据古典概率计算公式即可.
【详解】
从袋中一次随机摸出2个球,共有6种基本事件,
其中摸出的2个球的编号之和大于4的事件为,四种基本事件数,因此概率为.
故选:A.
7.C
【分析】
列出所有可能,再找出符合要求的情况即可得.
【详解】设这几个球中,红球分别为、、,白球分别为、,
则甲、乙两同学先后取出的两球可能的情况有:
、、、、、、、、、、
、、、、、、、、、、共二十种,
其中取到不同颜色球的情况有:
、、、、、、、、、、、共十二种,
故其概率为.
故选:C.
8.C
【分析】记6个模块分别为,求出总的基本事件数,然后求出甲、乙选择都不同的基本事件数,利用间接法求概率.
【详解】记6个模块分别为,
则甲从中选择2个共有共种不同的选择,
而甲每种的选择中乙与甲都不同有6种,
所以甲、乙各选2个共有种不同选择,而甲、乙选择都不同有种不同选择,
所以甲、乙选修的模块中至少有1个相同的概率.
故选:C.
9.ACD
【分析】
根据古典概型求解概率即可比较求解.
【详解】
A项,P(点数为奇数) P(点数为偶数);
B, 同时抛掷两枚硬币,共有4种情况:正正;正反;反正;正反.
则 P(恰有一枚正面向上),P(两枚都正面向上)=;概率不相等,故B错误,
C项,P(牌色为红) P(牌色为黑) ;
D项,P(同奇或同偶)=P(奇偶不同) .
故选:ACD.
10.ABC
【分析】画出树状图,结合图形及古典概型逐项分析判断.
【详解】画出树状图,结合图形
结合树状图可知:,
对于选项A:可知,故A正确;
对于选项B: 均有,故B正确;
对于选项C:因为,不经过数字5的路线有9条,所以,故C正确;
对于选项D:因为,所以,故D错误;
故选:ABC.
11.BC
【分析】由随机事件以及它的概率范围即可判断AB,由样本点,样本空间的定义即可判断CD.
【详解】对于A,他投篮一次,命中为随机事件,故A错误;
对于B,随机事件发生的可能性越大,它发生的概率越接近1,故B正确;
对于C,点数和为2当且仅当两枚骰子出现的点数都为1,这是有可能的,故C正确;
对于D,试验“连续投掷一枚均匀的骰子直到出现3点停止,观察投掷的次数”的样本空间为,故D错误.
故选:BC.
12.BCD
【分析】根据题意,列举法找到所有可能情况,由古典概型的概率计算公式分别计算.
【详解】设红骰子朝下的面上的点数为m,蓝骰子朝下的面上的点数为n,样本点为,
则样本空间为,则,
事件表示“两枚骰子的点数之和为”,
,
所以,故A错误;
事件表示“红色骰子的点数是偶数”,
所以,故B正确;
事件表示“两枚骰子的点数相同”,
,
所以,故C正确;
事件表示“至少一枚骰子的点数是偶数”,
,
所以,故D正确.
故选:BCD
13.12
【分析】根据列举法,结合古典概型的概率计算公式求解即可.
【详解】由题意得,一枚股子连抛两次的所有可能情况共36种,
事件A的所有可能情况为,共6种,
事件B的所有可能情况为,共6种,
事件AB的所有可能情况为,共1种,
所以,,,
所以.
故答案为:12
14.
【分析】根据集合意义即可求解.
【详解】区域,表示以圆心,半径为3的圆及其内部,
区域,表示以圆心,半径为1的圆,
结合图形可得所求概率.
故答案为:
15.
【分析】由可得答案.
【详解】因为,
所以.
故答案为:.
16. /0.3 /
【分析】根据给定的茎叶图,结合列举法求出古典概率;求出组学生该次测试成绩的平均成绩及方差,再利用分层抽样的方差公式计算即得.
【详解】由茎叶图知,组5名学生的测试成绩分别为,他们分别记为,
从5名学生任抽2人的样本空间,共10个,
成绩均在以上的事件,共3个,
所以这2个组长的成绩均在120分以上的概率为;
组5名学生测试成绩的平均分为,
方差为,而组学生的平均成绩为,方差为,
因此新数据组的平均分,
方差.
故答案为:;
17.(1)
(2)80
(3)
【分析】(1)根据各矩形面积之和为1,列式计算,即可求得a的值;
(2)根据频率分布直方图,结合中位数的求解方法,即可求得答案;
(3)求出内的人数之比,根据分层抽样可求得两组各抽取的人数,列举出从这5人中任意选取2人的所有可能情况,再列举出这2人中至少有1人成绩不低于90分的情况,根据古典概型的概率公式,即可求得答案.
【详解】(1)由频率分布直方图,得,
解得;
(2)由频率分布直方图,得,
,
则估计这600名学生成绩的中位数为80;
(3)由题意得,成绩在的频率为,
成绩在的频率为,频率之比为,
所以按分层抽样的方法从中选取5人,成绩在的学生有2人,分别记为,
成绩在的学生有3人,分别记为,
从这5人中任意选取2人,有,共10种选法,
其中至少有1人成绩不低于90分的选法有,,共9种,
所以这2人中至少有1人成绩不低于90分的概率.
18.(1),中位数为
(2)
【分析】(1)由概率和为1计算的值,由频率分布直方图中位数的计算公式计算中位数.
(2)根据频率分布直方图计算成绩在与的学生人数,列举法分别求出随机抽取2人总的情况数和中抽取2人的情况数,做比即可求出概率.
【详解】(1)由题知,, 解得.
,
,
故设中位数为,则,则,解得,
所以本次全市统考物理成绩的中位数为68分.
(2)由题知,样本中物理成绩在的学生人数为,设为,
物理成绩在的学生人数为,设为,
从这7人中随机抽取2人的所有情况为,,,,共21种不同情况,
记事件为“这2人的物理成绩均不低于90分”,则事件包含的情况有,共6种不同情况,
,所以这2人的物理成绩均不低于90分的概率为.
19.(1);;
(2)平均值81.5,中位数82;
(3)
【分析】(1)根据频率定义即可求出,再根据小矩形面积和为1即可求出值;
(2)根据平均数和中位数定义计算即可;
(3)列出所有情况和满足题意的情况,再利用古典概率公式即可.
【详解】(1)由直方图可知,乙样本中数据在的频率为,
则,解得;
由乙样本数据直方图可知,,
解得;
(2)甲样本数据的平均值估计值为
,
乙样本数据直方图中前3组的频率之和为,
前4组的频率之和为,
所以乙样本数据的中位数在第4组,设中位数为,
,
解得,所以乙样本数据的中位数为82.
(3)由频率分布直方图可知从分数在和的学生中分别抽取2人和4人,
将从分数在中抽取的2名学生分别记为,从分数在中抽取的4名学生分别记为,
则从这6人中随机抽取2人的基本事件有
,共15个,
所抽取的两人分数都在中的基本事件有6个,所以所求概率为.
20.(1)
(2)97.5
(3)
【分析】(1)根据频率分布直方图中各小矩形的面积之和为1计算即可;
(2)根据频率分布直方图和中位数的定义进行计算即可;
(3)根据题意列出样本空间,根据古典概型概率计算公式求解即可.
【详解】(1)由,
可得.
(2)由(1)知样本数据中数学考试成绩90分以下的所占比例为,
110分以下的所占比例为,
因此,中位数一定位于内,由,
可以估计样本数据的中位数约为97.5分,
据此可以估计该校高一上学期期末数学考试成绩的中位数约为97.5分.
(3)由题意分数段的人数为,
分数段的人数为,
用按比例分配的分层随机抽样的方法抽取5名学生,
则需在分数段内抽取2人,分别记为,,
分数段内抽取3人,分别记为,,.
设“从这5名学生中任取2人,至少有1人成绩在)内”为事件,
则样本空间,共包含10个样本点,
而事件包含7个样本点,所以,
故抽取的这2名学生至少有1人成绩在内的概率为.
21.(1);
(2).
【分析】(1)根据给定的频率分布直方图,利用面积法列式计算即得.
(2)求出两段抽取的人数,再利用列举法求出古典概率.
【详解】(1)分数在的频率为0.3,依题意,有奖问答的获奖分数线,
则,解得,
所以这次有奖问答的获奖分数线约为.
(2)分数在的频率分别为,因此抽取的4人中,分数在内的抽1人,记为,
分数在内的抽3人,依次记为,
抽取2人依次分享的试验样本空间,共12个结果,
第一个分享的得分在的事件,共9个结果,
所以第一个分享的网友得分在的概率.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
