青岛版八年级上册数学第一章全等三角形课件(共69张PPT)(共69张PPT)
文档属性
| 名称 | 青岛版八年级上册数学第一章全等三角形课件(共69张PPT)(共69张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-21 13:48:48 | ||
图片预览








文档简介
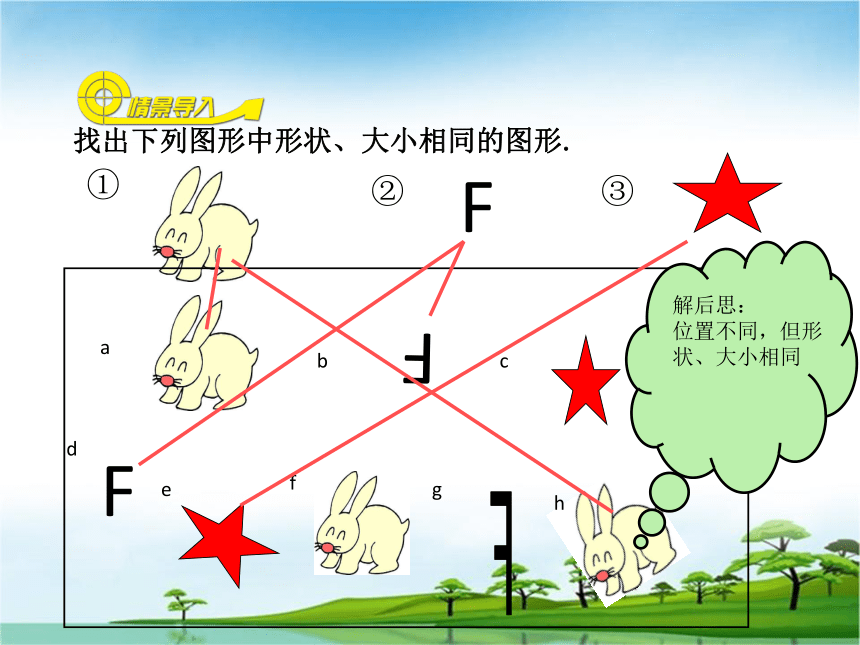
课件69张PPT。 全等三角形1.1①②③找出下列图形中形状、大小相同的图形.FFFFadcbhgfe1.知识目标
(1)了解全等形和全等三角形的概念,掌握全等三角形的性质.
(2)能正确表示两个全等三角形,能找出全等三角形的对应元素.
2.教学重点
全等三角形的概念和性质.
3.教学难点
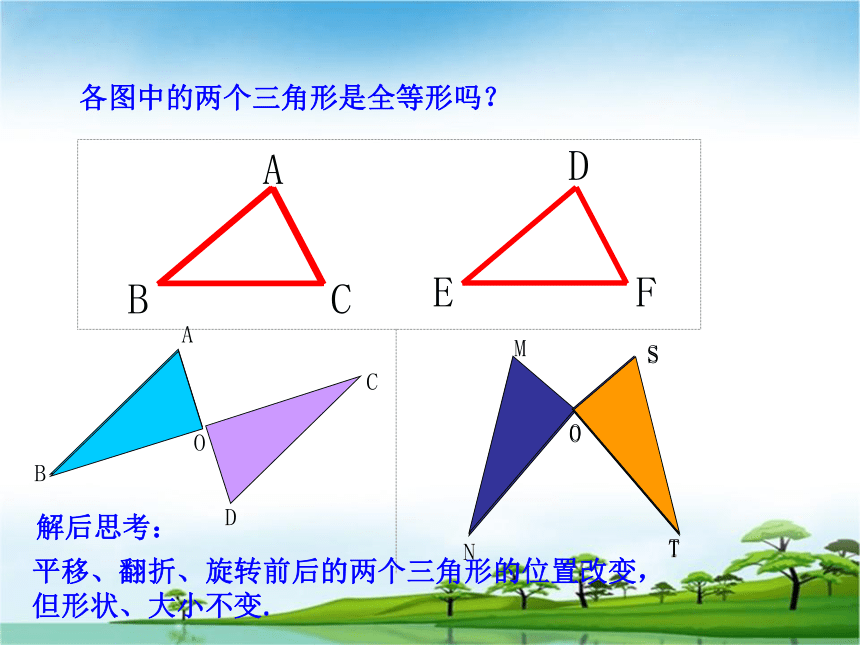
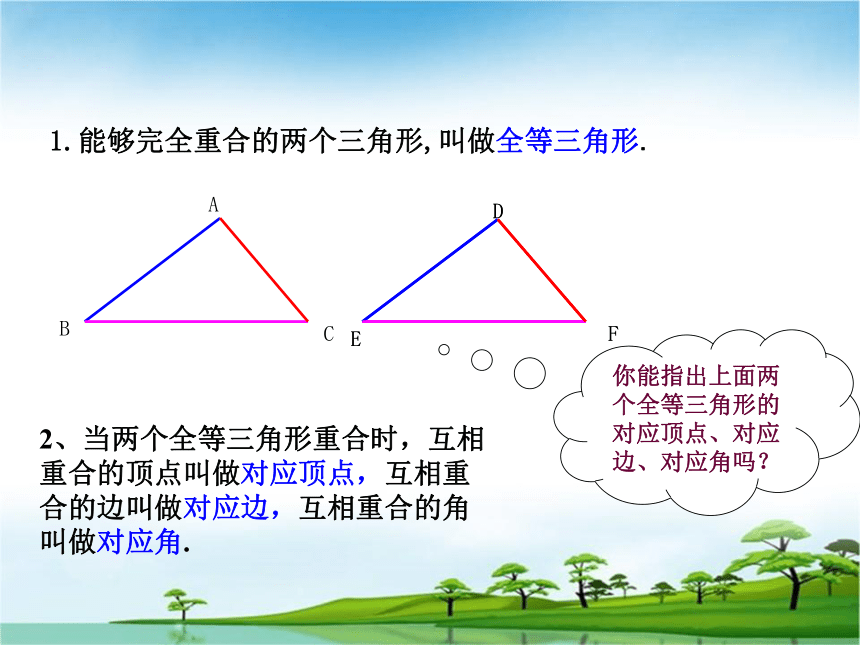
正确寻找全等三角形的对应元素.同一张底片洗出的照片能够完全重合的两个平面图形称为全等形.两张纸重合后剪纸,得到的两个图形的形状相同,大小相等.ABCDEF各图中的两个三角形是全等形吗?解后思考:平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变.1.能够完全重合的两个三角形,叫做全等三角形.2、当两个全等三角形重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角.你能指出上面两个全等三角形的对应顶点、对应边、对应角吗? “全等”用符号“≌ ”,表示图中的△ABC和△DEF全等,3、全等三角形的表示法记作△ABC≌ △DEF,读作△ABC全等于△DEF.注意记两个三角形全等时,通常把表示对应顶点的字母
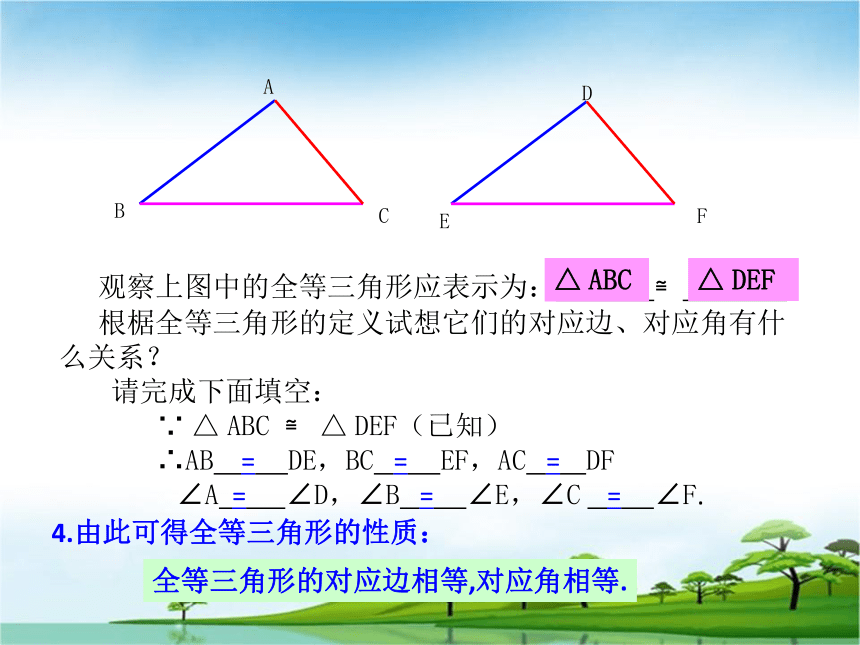
写在对应的位置上. 观察上图中的全等三角形应表示为: ≌ 。 根椐全等三角形的定义试想它们的对应边、对应角有什么关系?
请完成下面填空:
∵ △ ABC ≌ △ DEF(已知)
∴AB = DE,BC = EF,AC = DF
∠A = ∠D,∠B = ∠E,∠C = ∠F.4.由此可得全等三角形的性质:全等三角形的对应边相等,对应角相等.△ ABC△ DEF全等三角形性质的几何语言∵△ABC≌△DEF(已知) ∴AB=DE, AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等) 例1 如图:图中的两个三角形全等,A和B,C和D 是对应顶点.(1)用符号表示这两个三角形全等;(2)写出它们的对应角,对应边;(3)用等号表示各对应角,各对应边之间的关系.解:(2)?A和 ?B ,? C和?D, ?AOC和?BOD,
AO和BO,CO和DO,AC和BD(3) ?A= ?B, ? C= ?D, ?AOC= ?BOD,
AO=BO,CO=DO,AC=BD.
例2 如图, AD平分∠BAC,AB=AC,△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由.ABD1 (C)(全等三角形的对应角相等) ∵AD平分∠BAC∴ ∠1= ∠2,因此将图形沿AD对折时, AC与AB重合.∵AB=AC,∴点C与点B重合,也就是△ABD与△ACD重合∴ △ABD ≌ △ACD∴BD=CD(全等三角形的对应边相等)∠B=∠C解: 1、能够 的两个平面图形叫做全等形.两个三角形重合时,互相 _的顶点叫做对应顶点.记两个全等三角形时,通常把表示 _顶点的字母写在_ ___的位置上. 2、如图△ABC≌ △ADE,若∠D=∠B, ∠C= ∠AED,则∠DAE= ; ∠DAB= .完全重合重合重合相对应∠BAC∠EAC3、若△ABC≌△DEF,AC和DF,AB与DE是对应边,∠A=40°,∠B=30°BC=5cm,那么∠DFE=_____.EF=_________. 4、判定下列叙述是否正确 A、等边三角形都全等.( ) B、全等三角形的面积、周长相等.( ) C、形状相同的两个三角形全等.( ) D、有一边相等的两个等腰直角三角形全等.( ) 110° 5cm√×××5.如图,△ABC≌△DEC,CA和CD,CB和CE是对应边, ∠ ACD和∠BCE相等吗?为什么? 因为△DEC≌ △ABC,所以∠ DCE =∠ACB
又因为 ∠ ACD = ∠ DCE - ∠ 1
∠BCE = ∠ACB - ∠ 1
所以 ∠ ACD = ∠BCE
6.已知△ABC≌△DEF, △ABC的三边分别为3,m,n, △DEF的三边分别为5,p,q,若△ABC的三边均为整数,求m+n+p+q的最大值. 解: ∵△ABC≌△DEF ∴根据全等三角形对应边相等,m=5或n=5,不妨设m=5,在△ABC中,2<n<8, ∵n为整数, ∴n的最大值等于7,相应地,p和q应分别取3和7,
∴ m+n+p+q=5+7+3+7=22.拔尖自助餐1、如右图,已知△ABD≌△ACE, 且∠1=45°,∠ADB=95°,则 ∠AEC= ∠C= .2、如右图,已知△ABC≌△DFE, 且AC与DE是对应边,若BE=14cm, FC=4cm,则BC= .50°95° 9cm 课堂巩固 3、△AOC≌△BOD,∠A与∠B,∠C与∠D是对应角, △AOC的周长为9cm,OC=2cm,AO=3cm.则BO=______,
BD=_____. 4、△ABC≌△DCB,A与D,B 与C是对应顶点, ∠DCB=55°, ∠BDC=105°则∠ABD=______. 3cm4cm75° 4、如图△ABD≌ △EBC,
AB=3cm,BC=5cm,求DE的长.解:∵△ABD≌ △EBC
∴AB=EB,BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm这节课你有哪些收获?5.书写全等式时要求把对应字母放在对应的位置上.2. 叫做全等三角形. 1.能够完全重合的两个平面图形叫做 .全等形4.全等三角形的 和 相等.对应边对应角对应顶点 能够完全重合的两个三角形3.“全等”用符号“ ”来表示,读作“ ”对应边对应角全等于≌ 其中,互相重合的顶点叫做_ _;互相重合的边叫做____;互相重合的角叫做__ _.祝同学们学习进步!再见!BA'B'
C'
1.2 怎样判定三角形全等 小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?1.知识目标
(1)经历探索三角形全等条件的过程,体会分析问题的方法.积累数学活动的经验. (2)掌握三角形全等的“边角边”、“角边角”、“角角边”、“边边边”的条件. (3)利用“边角边”、“角边角”、“角角边” 、“边边边”判别两个三角形全等,解决一些简单的实际问题.2.教学重点
全等三角形的判定.
3.教学难点
学会如何运用三角形的判定定理和解题技巧来解决问题. △ABC与 △A'B'C '满足上述六个条件中的一部分是否能保证△ ABC 与 △A'B'C'全等呢? 6选1 or 6选2
探索6选1:一个角对应相等的两个三角形不一定全等;一条边对应相等的两个三角形不一定全等;6选2: 两个角对应相等的两个三角形不一定全等;两条边对应相等的两个三角形不一定全等;一角和一边对应相等的两个三角形不一定全等; 可见:要使两个三角形全等,
应至少有 组元素对应相等.36选3边边边 (SSS)两边一角两角一边角角角两边和它的夹角(SAS)两边和它一边的对角两角和夹边(ASA)两角和一角的对边(AAS)××两边和其中一边的对角对应相等的两个三角形不一定全等.SSA31三个角对应相等的两个三角形不一定全等AAA三角形全等的3个判定公理和1个推论: 例1 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.答: △ABC≌△DCB
理由如下:∵ 在△ABC和△DCB中AB = DCAC = DB=BCCB∴ △ABC≌△DCB(SSS)(公共边)(已知)(已知) 例2 如图OP是∠ MON的角平分线, C是OP上的一点,CA⊥ OM, CB⊥ON,垂足分别为A,B, △ AOC ≌ △ BOC吗 ?为什么?解: △ AOC ≌ △ BOC.∵ CA ⊥ OM, CB⊥ON.∴ ∠ CAO= ∠ CBO=90 ° .∵ OP是∠ MON的平分线,∴ ∠ AOC= ∠ BOC .又∵ OC= OC .根据“AAS”,可得.∴ △ AOC ≌ △ BOC .例3 如图,AC和BD相交于点O,OA=OC,OB=OD
求证:DC∥AB
1.如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;AB=AC∠BDA=∠CDA∠B=∠C2.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS ”为依据,
还缺条件______;若要以“ASA ”为依据,
还缺条件 ;
若要以“AAS ”为依据,
还缺条件_______ .
AB=DE ∠ACB=∠F ∠A=∠D 3.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CF(已知),ADBCFE∴AE-FE=CF-EF(等量减等量,差相等).即AF=CE.在△AFD和△CEB中,
∴△AFD≌△CEB(SAS).解:∵ ∠CAE=∠BAD(已知),∴ ∠CAE+∠BAE=∠BAD+∠BAE
(等量减等量,差相等).即∠BAC=∠DAE.在△ABC和△ADE中, ∴△ABC≌ △ADE(AAS). 5.“三月三,放风筝”如图是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC.请用所学的知识给予说明.解: 连接AC,∴△ADC≌△ABC(SSS).∴ ∠ABC=∠ADC.
(全等三角形的对应角相等)
在△ABC和△ADC中, 如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?解:AC=AD 在△ABC和△ABD中
AB=AB ,
∠1=∠2,
BC=BD.
∴ △ABC≌△ABD (SAS).
∴ AC=AD.拔尖自助餐 1. 测量如图河的宽度,某人在河的对岸找到一参照物树木A,视线AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75 m)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步到C处,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米.
15ABODC2. 如图,M是AB的中点 ,∠1 = 2 ,MC=MD.
试说明△ACM ≌ △BDM .证明: ∵ M是AB的中点 (已知),
∴ MA=MB(中点定义).
在△ACM 和△BDM中,
MA=MB(已证),
∠1 = ∠2 (已知),
MC=MD(已知).
∴△ACM ≌ △BDM (SAS).3.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=BF,
求证:∠E=∠C证明:∵ AD=FB,∴∴ AD+DB=BF+DB.即AB=FD.在△ABC和△FDE中,AC=FE,
BC=DE,
AB=FD.△ABC≌△FDE(SSS).∴∠E=∠C.4.如图,AB=AD,CB=CD.
求证: AC 平分∠BAD5.点M是等腰梯形ABCD底边AB的中点,
求证:⑴△AMD≌△BMC ;
⑵DM=CM,∠ADM=∠BCM.证明:⑴ ∵ 点M是等腰梯形ABCD底边AB的中点,
∴ AD=BC ,∠A=∠B,AM=BM.在△ADM和△BCM中,∴△AMD≌△BMC (SAS).∴ DM=CM,∠ADM=∠BCM.⑵ ∵ △AMD≌△BMC, 这节课你有哪些收获?祝同学们学习进步!再见!尺规作图1.3古希腊认为,所有图形都是由直线和圆弧构成的,圆是最完美的图形.他们确信仅靠圆规和直尺就可以绘出图形来.他们还认为,依据少量假设,通过逻辑把握的东西最可靠.尺规作图1.知识目标
(1)理解尺规作图和基本作图的定义;
(2)掌握基本作图的作法,会作一条线段等于已知线段和作一个角等于已知角;
(3)会利用基本作图来进行作图举例(如:已知两边及夹角、三边或两角及夹边等.)2.教学重点
利用五个基本作图解决一些实际问题.
3.教学难点
将几何作图与几何设计综合在一起,解决实
际问题的动手作图能力.尺规作图:在几何里,把只能使用没有刻度
的直尺和圆规这两种工具作几何图形的方法
称为尺规作图.
尺:没有刻度的直尺;规:圆规
直尺的功能:在两点间连接一条线段,
将线段向两方延长
圆规的功能:作一个圆;作一段弧
最基本,最常用的尺规作图,通常称基本作图. 则线段AC 就是所要画的线段. (1)作射线AB; (2)以A为圆心,MN长为半径画弧, 交射线AB于点C;作法:如图,已知线段MN=a.1.作一条线段等于已知线段求作:求作一条线段等于a.如图,已知∠AOB ,
求作一个角等于∠AOB. 2.作一个角等于已知角 作法:(1)画射线O′A′; (2)以点O 为圆心,以适当长为半径画
弧,交OA 于C ,交OB 于D ;(3)以点O′为圆心,以OC 长为半径画弧,
交O′ A′于C′. (4)以点C′为圆心,以CD 长为半径画弧,
交前一条弧于D′.O ′A ′(5)经过点D′画射线O′ B′,则∠A′ O′ B′
就是所要画的角. 为什么?例1 已知三边作三角形.
已知:如图,线段a,b,c.
求作:△ABC,使AB = c,AC = b,BC = a.
作法:作线段AB = c;
以A为圆心b为半径作弧,
以B为圆心a为半径作弧与前弧相交于C;
连接AC,BC.
则△ABC就是所求作的三角形.例3 已知两角及夹边作三角形.
已知:如图,∠1,∠2,线段m .
求作:△ABC,使∠A=∠1,
∠B=∠2,AB=m.
作法:
作线段AB=m;
在AB的同旁
作∠A=∠1,作∠B=∠2,
∠A与∠B的另一边相交于C.
则△ABC就是所求作的三角形.1. 已知线段AB和CD,如下图,求作一线段,使它的长度等于AB + 2CD.所以EF就是所求作的线段.2 如图,已知∠A ,∠B,求作一个角,使它等于∠A+∠B.所以∠CDF就是所求作的角.3.用直尺和圆规作一个角等于已知角的示意图如下,则说明的 依据是( )
A.SAS B.ASA
C.AAS D.SSS
D4.如图,某人不小心把一块三角形的玻璃打碎成三块,现在要到玻璃店去配一块完全一样的玻璃,那么他最少要( )A.带①去 B.带②去
C.带③去 D.带①和②去C (1)作射线AC;A C (2)以点A为圆心, a以a长为半径画弧,交射线AC于点D;D(3)以点D为圆心, 以a长为半径
画弧,交射线AC于点B;BAB 就是所求作的线段.已知:
求作:线段AB ,使
作法 :线段a,线段AB=2a用尺规作图:任意画一条线段a,求作一条线段AB,使AB=2a.拔尖自助餐
一、选择题
1.尺规作图用的工具是( )
A. 三角尺和圆规 B.刻度尺和圆规
C. 没有刻度的直尺和圆规 D.以上都不对
2. 下列作图语句错误的个数是 ( )
(1)过A.B.C三点作直线.(2)延长射线OM到点A.
(3)延长线段AB. (4)以点o为圆心画弧.
A . 1 B.2 C.3 D .4
二、填空题
1.已知线段AB,
求作:线段A′B′,使A′B′=AB.
作法:(1)作 A′C′.
(2)以 为圆心,以 为半径画弧,交射线A′C′
于点B′, _________ 就是所求作的线段.C点A′ABA′B′的长D射线3.已知线段a,b,求作线段AB,使AB=a+bab解:作射线AC.
以点A为圆心,以a长为半径画弧,交AC于点D.
以点D为圆心,以b的长为半径画弧,交AC于点B.
则线段AB即所求作的线段.这节课你有哪些收获?通过本节学习,应理解一些作图语句.
点x作直线;或作直线xx,射线xx.
连结两点x,x;或连结xx;
在xx上截取xx=xx;
以点x为圆心,xx为半径作圆(弧);(交xx于x点)
分别以点x为圆心,以xx为半径作 弧,两弧相交于x点.?两个基本作图
(1)作一条线段等于已知线段(2)作一个角等于已知角祝同学们学习进步!再见!
(1)了解全等形和全等三角形的概念,掌握全等三角形的性质.
(2)能正确表示两个全等三角形,能找出全等三角形的对应元素.
2.教学重点
全等三角形的概念和性质.
3.教学难点
正确寻找全等三角形的对应元素.同一张底片洗出的照片能够完全重合的两个平面图形称为全等形.两张纸重合后剪纸,得到的两个图形的形状相同,大小相等.ABCDEF各图中的两个三角形是全等形吗?解后思考:平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变.1.能够完全重合的两个三角形,叫做全等三角形.2、当两个全等三角形重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角.你能指出上面两个全等三角形的对应顶点、对应边、对应角吗? “全等”用符号“≌ ”,表示图中的△ABC和△DEF全等,3、全等三角形的表示法记作△ABC≌ △DEF,读作△ABC全等于△DEF.注意记两个三角形全等时,通常把表示对应顶点的字母
写在对应的位置上. 观察上图中的全等三角形应表示为: ≌ 。 根椐全等三角形的定义试想它们的对应边、对应角有什么关系?
请完成下面填空:
∵ △ ABC ≌ △ DEF(已知)
∴AB = DE,BC = EF,AC = DF
∠A = ∠D,∠B = ∠E,∠C = ∠F.4.由此可得全等三角形的性质:全等三角形的对应边相等,对应角相等.△ ABC△ DEF全等三角形性质的几何语言∵△ABC≌△DEF(已知) ∴AB=DE, AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等) 例1 如图:图中的两个三角形全等,A和B,C和D 是对应顶点.(1)用符号表示这两个三角形全等;(2)写出它们的对应角,对应边;(3)用等号表示各对应角,各对应边之间的关系.解:(2)?A和 ?B ,? C和?D, ?AOC和?BOD,
AO和BO,CO和DO,AC和BD(3) ?A= ?B, ? C= ?D, ?AOC= ?BOD,
AO=BO,CO=DO,AC=BD.
例2 如图, AD平分∠BAC,AB=AC,△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由.ABD1 (C)(全等三角形的对应角相等) ∵AD平分∠BAC∴ ∠1= ∠2,因此将图形沿AD对折时, AC与AB重合.∵AB=AC,∴点C与点B重合,也就是△ABD与△ACD重合∴ △ABD ≌ △ACD∴BD=CD(全等三角形的对应边相等)∠B=∠C解: 1、能够 的两个平面图形叫做全等形.两个三角形重合时,互相 _的顶点叫做对应顶点.记两个全等三角形时,通常把表示 _顶点的字母写在_ ___的位置上. 2、如图△ABC≌ △ADE,若∠D=∠B, ∠C= ∠AED,则∠DAE= ; ∠DAB= .完全重合重合重合相对应∠BAC∠EAC3、若△ABC≌△DEF,AC和DF,AB与DE是对应边,∠A=40°,∠B=30°BC=5cm,那么∠DFE=_____.EF=_________. 4、判定下列叙述是否正确 A、等边三角形都全等.( ) B、全等三角形的面积、周长相等.( ) C、形状相同的两个三角形全等.( ) D、有一边相等的两个等腰直角三角形全等.( ) 110° 5cm√×××5.如图,△ABC≌△DEC,CA和CD,CB和CE是对应边, ∠ ACD和∠BCE相等吗?为什么? 因为△DEC≌ △ABC,所以∠ DCE =∠ACB
又因为 ∠ ACD = ∠ DCE - ∠ 1
∠BCE = ∠ACB - ∠ 1
所以 ∠ ACD = ∠BCE
6.已知△ABC≌△DEF, △ABC的三边分别为3,m,n, △DEF的三边分别为5,p,q,若△ABC的三边均为整数,求m+n+p+q的最大值. 解: ∵△ABC≌△DEF ∴根据全等三角形对应边相等,m=5或n=5,不妨设m=5,在△ABC中,2<n<8, ∵n为整数, ∴n的最大值等于7,相应地,p和q应分别取3和7,
∴ m+n+p+q=5+7+3+7=22.拔尖自助餐1、如右图,已知△ABD≌△ACE, 且∠1=45°,∠ADB=95°,则 ∠AEC= ∠C= .2、如右图,已知△ABC≌△DFE, 且AC与DE是对应边,若BE=14cm, FC=4cm,则BC= .50°95° 9cm 课堂巩固 3、△AOC≌△BOD,∠A与∠B,∠C与∠D是对应角, △AOC的周长为9cm,OC=2cm,AO=3cm.则BO=______,
BD=_____. 4、△ABC≌△DCB,A与D,B 与C是对应顶点, ∠DCB=55°, ∠BDC=105°则∠ABD=______. 3cm4cm75° 4、如图△ABD≌ △EBC,
AB=3cm,BC=5cm,求DE的长.解:∵△ABD≌ △EBC
∴AB=EB,BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm这节课你有哪些收获?5.书写全等式时要求把对应字母放在对应的位置上.2. 叫做全等三角形. 1.能够完全重合的两个平面图形叫做 .全等形4.全等三角形的 和 相等.对应边对应角对应顶点 能够完全重合的两个三角形3.“全等”用符号“ ”来表示,读作“ ”对应边对应角全等于≌ 其中,互相重合的顶点叫做_ _;互相重合的边叫做____;互相重合的角叫做__ _.祝同学们学习进步!再见!BA'B'
C'
1.2 怎样判定三角形全等 小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?1.知识目标
(1)经历探索三角形全等条件的过程,体会分析问题的方法.积累数学活动的经验. (2)掌握三角形全等的“边角边”、“角边角”、“角角边”、“边边边”的条件. (3)利用“边角边”、“角边角”、“角角边” 、“边边边”判别两个三角形全等,解决一些简单的实际问题.2.教学重点
全等三角形的判定.
3.教学难点
学会如何运用三角形的判定定理和解题技巧来解决问题. △ABC与 △A'B'C '满足上述六个条件中的一部分是否能保证△ ABC 与 △A'B'C'全等呢? 6选1 or 6选2
探索6选1:一个角对应相等的两个三角形不一定全等;一条边对应相等的两个三角形不一定全等;6选2: 两个角对应相等的两个三角形不一定全等;两条边对应相等的两个三角形不一定全等;一角和一边对应相等的两个三角形不一定全等; 可见:要使两个三角形全等,
应至少有 组元素对应相等.36选3边边边 (SSS)两边一角两角一边角角角两边和它的夹角(SAS)两边和它一边的对角两角和夹边(ASA)两角和一角的对边(AAS)××两边和其中一边的对角对应相等的两个三角形不一定全等.SSA31三个角对应相等的两个三角形不一定全等AAA三角形全等的3个判定公理和1个推论: 例1 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.答: △ABC≌△DCB
理由如下:∵ 在△ABC和△DCB中AB = DCAC = DB=BCCB∴ △ABC≌△DCB(SSS)(公共边)(已知)(已知) 例2 如图OP是∠ MON的角平分线, C是OP上的一点,CA⊥ OM, CB⊥ON,垂足分别为A,B, △ AOC ≌ △ BOC吗 ?为什么?解: △ AOC ≌ △ BOC.∵ CA ⊥ OM, CB⊥ON.∴ ∠ CAO= ∠ CBO=90 ° .∵ OP是∠ MON的平分线,∴ ∠ AOC= ∠ BOC .又∵ OC= OC .根据“AAS”,可得.∴ △ AOC ≌ △ BOC .例3 如图,AC和BD相交于点O,OA=OC,OB=OD
求证:DC∥AB
1.如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;AB=AC∠BDA=∠CDA∠B=∠C2.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS ”为依据,
还缺条件______;若要以“ASA ”为依据,
还缺条件 ;
若要以“AAS ”为依据,
还缺条件_______ .
AB=DE ∠ACB=∠F ∠A=∠D 3.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CF(已知),ADBCFE∴AE-FE=CF-EF(等量减等量,差相等).即AF=CE.在△AFD和△CEB中,
∴△AFD≌△CEB(SAS).解:∵ ∠CAE=∠BAD(已知),∴ ∠CAE+∠BAE=∠BAD+∠BAE
(等量减等量,差相等).即∠BAC=∠DAE.在△ABC和△ADE中, ∴△ABC≌ △ADE(AAS). 5.“三月三,放风筝”如图是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC.请用所学的知识给予说明.解: 连接AC,∴△ADC≌△ABC(SSS).∴ ∠ABC=∠ADC.
(全等三角形的对应角相等)
在△ABC和△ADC中, 如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?解:AC=AD 在△ABC和△ABD中
AB=AB ,
∠1=∠2,
BC=BD.
∴ △ABC≌△ABD (SAS).
∴ AC=AD.拔尖自助餐 1. 测量如图河的宽度,某人在河的对岸找到一参照物树木A,视线AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75 m)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步到C处,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米.
15ABODC2. 如图,M是AB的中点 ,∠1 = 2 ,MC=MD.
试说明△ACM ≌ △BDM .证明: ∵ M是AB的中点 (已知),
∴ MA=MB(中点定义).
在△ACM 和△BDM中,
MA=MB(已证),
∠1 = ∠2 (已知),
MC=MD(已知).
∴△ACM ≌ △BDM (SAS).3.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=BF,
求证:∠E=∠C证明:∵ AD=FB,∴∴ AD+DB=BF+DB.即AB=FD.在△ABC和△FDE中,AC=FE,
BC=DE,
AB=FD.△ABC≌△FDE(SSS).∴∠E=∠C.4.如图,AB=AD,CB=CD.
求证: AC 平分∠BAD5.点M是等腰梯形ABCD底边AB的中点,
求证:⑴△AMD≌△BMC ;
⑵DM=CM,∠ADM=∠BCM.证明:⑴ ∵ 点M是等腰梯形ABCD底边AB的中点,
∴ AD=BC ,∠A=∠B,AM=BM.在△ADM和△BCM中,∴△AMD≌△BMC (SAS).∴ DM=CM,∠ADM=∠BCM.⑵ ∵ △AMD≌△BMC, 这节课你有哪些收获?祝同学们学习进步!再见!尺规作图1.3古希腊认为,所有图形都是由直线和圆弧构成的,圆是最完美的图形.他们确信仅靠圆规和直尺就可以绘出图形来.他们还认为,依据少量假设,通过逻辑把握的东西最可靠.尺规作图1.知识目标
(1)理解尺规作图和基本作图的定义;
(2)掌握基本作图的作法,会作一条线段等于已知线段和作一个角等于已知角;
(3)会利用基本作图来进行作图举例(如:已知两边及夹角、三边或两角及夹边等.)2.教学重点
利用五个基本作图解决一些实际问题.
3.教学难点
将几何作图与几何设计综合在一起,解决实
际问题的动手作图能力.尺规作图:在几何里,把只能使用没有刻度
的直尺和圆规这两种工具作几何图形的方法
称为尺规作图.
尺:没有刻度的直尺;规:圆规
直尺的功能:在两点间连接一条线段,
将线段向两方延长
圆规的功能:作一个圆;作一段弧
最基本,最常用的尺规作图,通常称基本作图. 则线段AC 就是所要画的线段. (1)作射线AB; (2)以A为圆心,MN长为半径画弧, 交射线AB于点C;作法:如图,已知线段MN=a.1.作一条线段等于已知线段求作:求作一条线段等于a.如图,已知∠AOB ,
求作一个角等于∠AOB. 2.作一个角等于已知角 作法:(1)画射线O′A′; (2)以点O 为圆心,以适当长为半径画
弧,交OA 于C ,交OB 于D ;(3)以点O′为圆心,以OC 长为半径画弧,
交O′ A′于C′. (4)以点C′为圆心,以CD 长为半径画弧,
交前一条弧于D′.O ′A ′(5)经过点D′画射线O′ B′,则∠A′ O′ B′
就是所要画的角. 为什么?例1 已知三边作三角形.
已知:如图,线段a,b,c.
求作:△ABC,使AB = c,AC = b,BC = a.
作法:作线段AB = c;
以A为圆心b为半径作弧,
以B为圆心a为半径作弧与前弧相交于C;
连接AC,BC.
则△ABC就是所求作的三角形.例3 已知两角及夹边作三角形.
已知:如图,∠1,∠2,线段m .
求作:△ABC,使∠A=∠1,
∠B=∠2,AB=m.
作法:
作线段AB=m;
在AB的同旁
作∠A=∠1,作∠B=∠2,
∠A与∠B的另一边相交于C.
则△ABC就是所求作的三角形.1. 已知线段AB和CD,如下图,求作一线段,使它的长度等于AB + 2CD.所以EF就是所求作的线段.2 如图,已知∠A ,∠B,求作一个角,使它等于∠A+∠B.所以∠CDF就是所求作的角.3.用直尺和圆规作一个角等于已知角的示意图如下,则说明的 依据是( )
A.SAS B.ASA
C.AAS D.SSS
D4.如图,某人不小心把一块三角形的玻璃打碎成三块,现在要到玻璃店去配一块完全一样的玻璃,那么他最少要( )A.带①去 B.带②去
C.带③去 D.带①和②去C (1)作射线AC;A C (2)以点A为圆心, a以a长为半径画弧,交射线AC于点D;D(3)以点D为圆心, 以a长为半径
画弧,交射线AC于点B;BAB 就是所求作的线段.已知:
求作:线段AB ,使
作法 :线段a,线段AB=2a用尺规作图:任意画一条线段a,求作一条线段AB,使AB=2a.拔尖自助餐
一、选择题
1.尺规作图用的工具是( )
A. 三角尺和圆规 B.刻度尺和圆规
C. 没有刻度的直尺和圆规 D.以上都不对
2. 下列作图语句错误的个数是 ( )
(1)过A.B.C三点作直线.(2)延长射线OM到点A.
(3)延长线段AB. (4)以点o为圆心画弧.
A . 1 B.2 C.3 D .4
二、填空题
1.已知线段AB,
求作:线段A′B′,使A′B′=AB.
作法:(1)作 A′C′.
(2)以 为圆心,以 为半径画弧,交射线A′C′
于点B′, _________ 就是所求作的线段.C点A′ABA′B′的长D射线3.已知线段a,b,求作线段AB,使AB=a+bab解:作射线AC.
以点A为圆心,以a长为半径画弧,交AC于点D.
以点D为圆心,以b的长为半径画弧,交AC于点B.
则线段AB即所求作的线段.这节课你有哪些收获?通过本节学习,应理解一些作图语句.
点x作直线;或作直线xx,射线xx.
连结两点x,x;或连结xx;
在xx上截取xx=xx;
以点x为圆心,xx为半径作圆(弧);(交xx于x点)
分别以点x为圆心,以xx为半径作 弧,两弧相交于x点.?两个基本作图
(1)作一条线段等于已知线段(2)作一个角等于已知角祝同学们学习进步!再见!
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
