湘教版2023-2024学年八年级下册期中复习卷(含解析)
文档属性
| 名称 | 湘教版2023-2024学年八年级下册期中复习卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 386.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 00:00:00 | ||
图片预览



文档简介
湘教版2023-2024学年八年级下册期中复习卷
一、单选题(共10题,每小题3分,共30分)
1.如图,下列哪组条件不能判定四边形ABCD是平行四边形( )
A.AB∥CD,AB=CD B.AB∥CD,AD∥BC
C.OA=OC,OB=OD D.AB∥CD,AD=BC
2.下列几组数中,能作为直角三角形三边长度的是( )
A.1,1, B.2,3,4 C.3,4,5 D.5,7,9
3.下列多边形中,内角和与外角和相等的是( )
A.四边形 B.五边形 C.六边形 D.八边形
4.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( )
A.15 B.30 C.45 D.60
5.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1 B.4S2 C.4S2+S3 D.3S1+4S3
6.如果等边三角形的边长为3,那么连接各边中点所成的三角形的周长为( )
A.9 B.6 C.3 D.
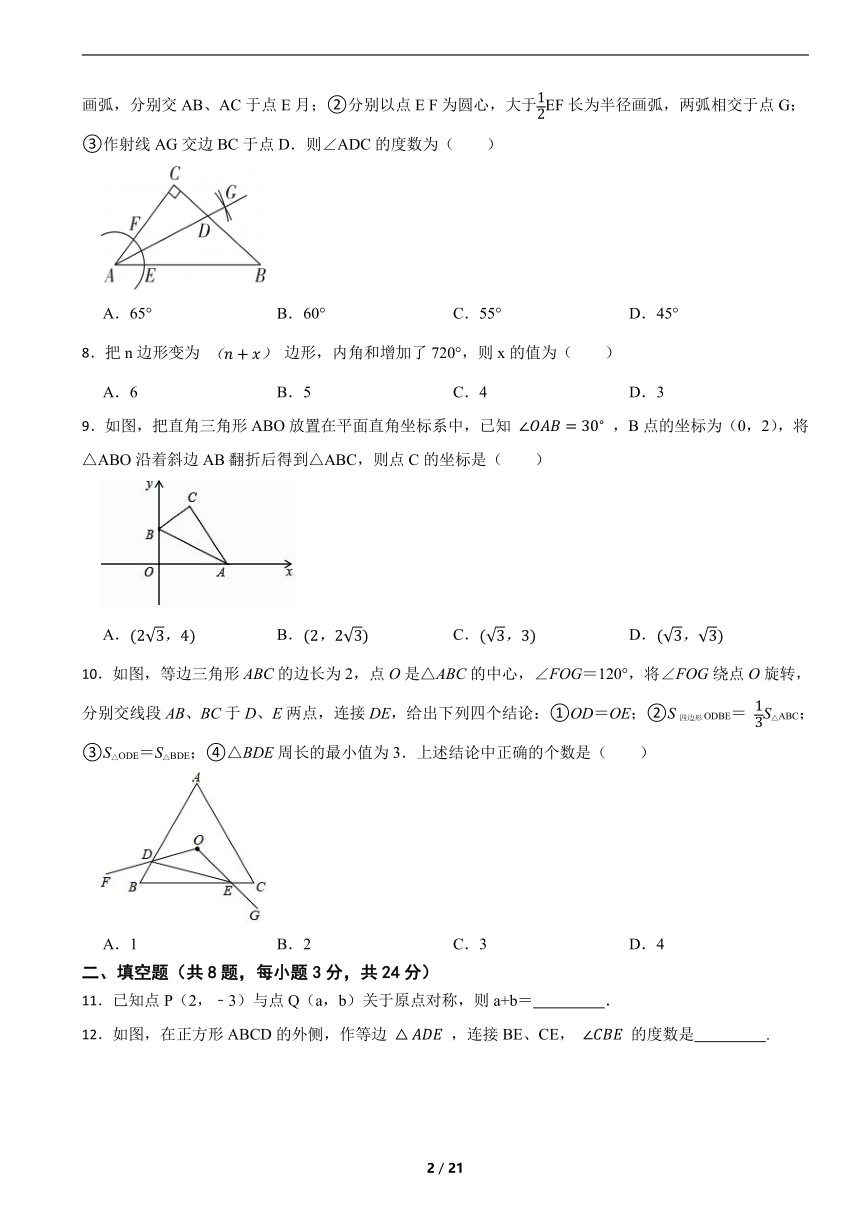
7.如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E月;②分别以点E F为圆心,大于EF长为半径画弧,两弧相交于点G;③作射线AG交边BC于点D.则∠ADC的度数为( )
A.65° B.60° C.55° D.45°
8.把n边形变为 边形,内角和增加了720°,则x的值为( )
A.6 B.5 C.4 D.3
9.如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为(0,2),将△ABO沿着斜边AB翻折后得到△ABC,则点C的坐标是( )
A. B. C. D.
10.如图,等边三角形ABC的边长为2,点O是△ABC的中心,∠FOG=120°,将∠FOG绕点O旋转,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:①OD=OE;②S四边形ODBE= S△ABC;③S△ODE=S△BDE;④△BDE周长的最小值为3.上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共8题,每小题3分,共24分)
11.已知点P(2,﹣3)与点Q(a,b)关于原点对称,则a+b= .
12.如图,在正方形ABCD的外侧,作等边 ,连接BE、CE, 的度数是 .
13.如图,在四边形中,O是中点,,,若,则 .
14.如图,菱形 的对角线交于点 是线段 上一动点, E 是线段 AB上一个动点,则 的最小值为 .
15.如图,△ABC中,AP垂直∠B的平分线BP于P.若△PBC的面积为6cm2,且△APB的面积是△APC的面积的2倍.则△APB的面积= cm2.
16.如图,将长方形沿翻折,点的对应点恰好落在边上,若,则的度数为 .
17.如图,长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG,将∠BEG对折,点B落在直线EG上的点B'处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A'处,得折痕EN.∠FEG=40°,则∠MEN= .
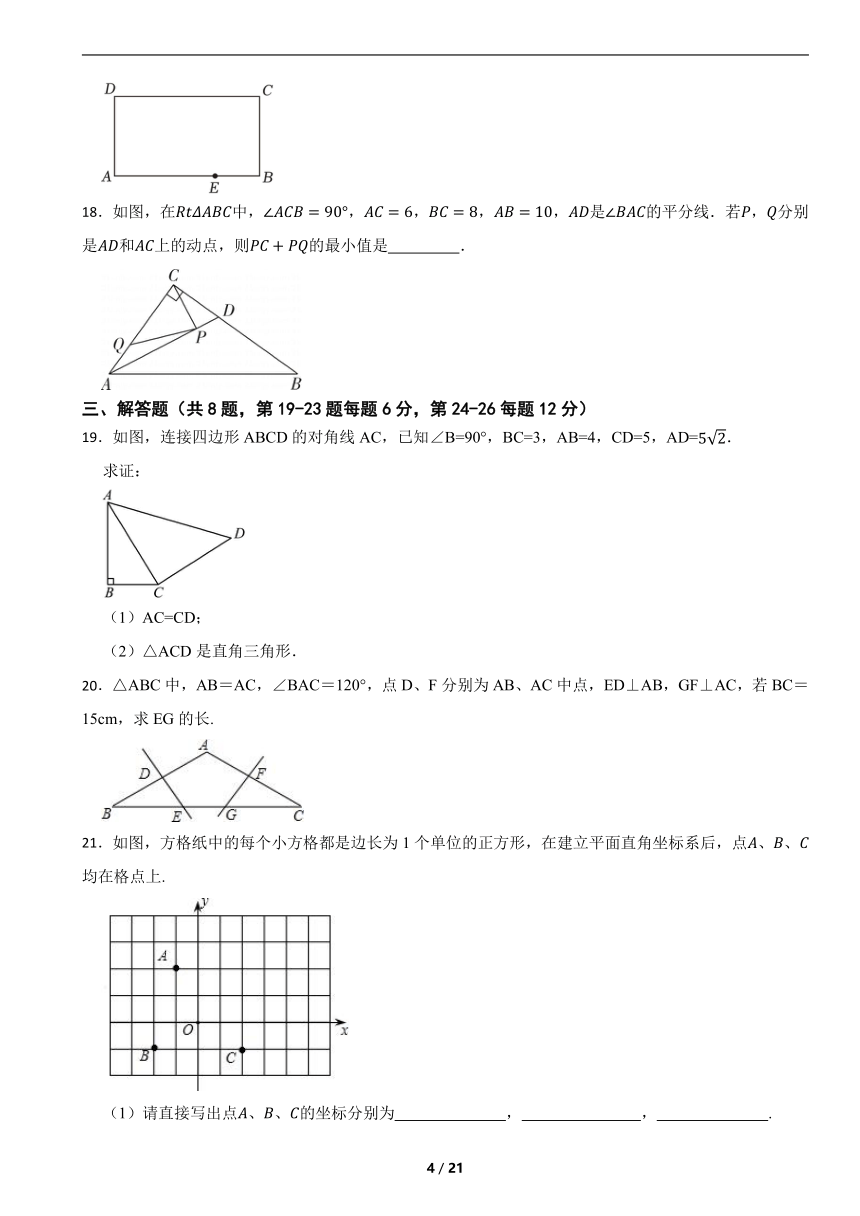
18.如图,在中,,,,,是的平分线.若,分别是和上的动点,则的最小值是 .
三、解答题(共8题,第19-23题每题6分,第24-26每题12分)
19.如图,连接四边形ABCD的对角线AC,已知∠B=90°,BC=3,AB=4,CD=5,AD=.
求证:
(1)AC=CD;
(2)△ACD是直角三角形.
20.△ABC中,AB=AC,∠BAC=120°,点D、F分别为AB、AC中点,ED⊥AB,GF⊥AC,若BC=15cm,求EG的长.
21.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点、、均在格点上.
(1)请直接写出点、、的坐标分别为 , , .
(2)若平移线段,使移动到的位置,请在图中画出移动后的位置,依次连接,,,,则四边形的面积为 ▲ .
22.nbsp;.如图,在ABCD平行四边形中,过点A作于点E,于点F,.求证:
(1);
(2)四边形ABCD是菱形.
23.如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,
(1)求∠ECF的度数;
(2)若CE=4,B′F=1,求线段BC的长和△ABC的面积.
24.在正方形ABCD中,点E,F,G分别在边AD,AB,CD上(点E、F、G不与正方形的顶点重合),BE,FG相交于点O,且FG⊥BE.
(1)猜想BE与FG的数量关系并证明;
(2)证明:DG=AF+AE;
(3)若AE= ,FG=4,请直接写出点C到直线BE的距离;
25.如图,四边形ABCD为正方形,E为AB的中点,作EF⊥AB交CD于F,连结AF,BF,作FG⊥BF交AC的延长线于G,AC与EF交于点O.
(1)设∠AFE=α,用含a的代数式表示∠G的度数.
(2)求证:AO=GC.
(3)如图,若△AFG的面积为15,求正方形ABCD的边长.
26.
(1)【情景引入】:
如图,、分别是的内角、的平分线,说明的理由.
(2)【深入探究】:
如图,、分别是的两个外角、的平分线,与之间的等量关系是 ;
如图,、分别是的一个内角和一个外角的平分线,与之间的等量关系是 .
(3)【拓展应用】:
请用以上结论解决下列问题:如图,在中,、分别平分、,、、分别在、、的延长线上,、分别平分、,、分别平分、.
,则的度数为 ;
,则的度数为 .
答案解析部分
1.【答案】D
【解析】【解答】根据平行四边形的判定,A、B、C均符合是平行四边形的条件,D则不能判定是平行四边形.
故答案为:D.
【分析】A.一组对边平行且相等是四边形是平行四边形;
B.两组边分别平行的四边形是平行四边形;
C.对角线互相平分的四边形是平行四边形;
D.一组对边平行,另一组对边相等的四边形不能判定为平行四边形,也可能是等腰梯形。
2.【答案】C
【解析】【解答】解:A、12+12≠( )2,故不是直角三角形,故此选项错误;
B、22+32≠42,故不是直角三角形,故此选项错误;
C、32+42=52,故是直角三角形,故此选项正确;
D、52+72≠92,故不是直角三角形,故此选项错误.
故答案为:C.
【分析】若一个三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形为直角三角形,据此判断.
3.【答案】A
【解析】【解答】解:设多边形的边数是n,则(n﹣2) 180=360,
解得n=4.
故选A.
【分析】设多边形的边数是n,根据多边形的内角和定理即可求解.
4.【答案】B
【解析】【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积= ×AB×DE=30,
故答案为:B.
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC=4,根据三角形的面积公式计算即可.
5.【答案】A
【解析】【解答】解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2= (a+c)(a﹣c)= a2﹣ c2,
∴S2=S1﹣ S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选A.
【分析】设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S1,S2,S3之间的关系,由此即可解决问题.
6.【答案】D
【解析】【解答】解:连接各边中点所成的线段是等边三角形的中位线,每条中位线的长是 ,故新成的三角形的周长为 ×3= .
故选D
【分析】等边三角形的边长为3,根据三角形的中位线定理可求出中点三角形的边长,所以中点三角形的周长可求解.
7.【答案】A
【解析】【解答】解:由作图可得:
AG是∠CAB的角平分线
∵∠CAB=50°
∴
在△ADC中,∠C=90°
∴∠ADC=180°-∠C-∠CAD=65°
故答案为:A
【分析】根据作图可知AG是∠CAB的角平分线,再根据角平分线性质可得,再根据三角形内角和定理即可求出答案.
8.【答案】C
【解析】【解答】把n边形变为(n+x)边形,内角和增加了720°,
根据内角和公式得
(n+x-2)×180°-(n-2)×180°=720°,
解得x=4,
故答案为:C.
【分析】根据内角和公式列出方程即可求解.
9.【答案】C
【解析】【解答】解: , , ,
, ,
过点C作 轴,垂直为D,则 .
, .
.
故答案为:C
【分析】先根据轴对称的性质可得△BOA≌△BCA,即可得出OB=BC=2, ∠CBA=∠OBA=60°,然后过点C作垂线,可得∠DCB=30°,根据直角三角形的性质可得DB,DC,从而得出点的坐标.
10.【答案】C
【解析】【解答】连接OB、OC,如图,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点O是△ABC的中心,
∴OB=OC,OB、OC分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=∠OCB=30°,
∴∠BOC=120°,即∠BOE+∠COE=120°,
而∠DOE=120°,即∠BOE+∠BOD=120°,
∴∠BOD=∠COE,
在△BOD和△COE中,
,
∴△BOD≌△COE(ASA),
∴BD=CE,OD=OE,
∴①符合题意;
∵△BOD≌△COE,
∴S△BOD=S△COE,
∴四边形ODBE的面积=S△OBC═ S△ABC,
故②符合题意;
作OH⊥DE于H,如图,则DH=EH,
∵∠DOE=120°,
∴∠ODE=∠OEH=30°,
∴OH= OE,HE= OH= OE,
∴DE= OE,
∴S△ODE= × OE× OE= OE2,
即S△ODE随OE的变化而变化,
而四边形ODBE的面积为定值,
∴S△ODE≠S△BDE;
故③不符合题意;
∵BD=CE,
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=2+DE=2+ OE,
当OE⊥BC时,OE最小,△BDE的周长最小,此时OE= ,
∴△BDE周长的最小值=2+1=3,
故④符合题意.
综上所述,正确的有①②④共3个.
故答案为:C.
【分析】利用旋转的性质,再结合三角形全等的判定和性质逐项判定即可。
11.【答案】1
【解析】【解答】解:∵点与点关于原点对称,
∴a=-2,b= 3,
∴a+b=-2+3=1,
故答案为:1.
【分析】关于原点对称的坐标特征得出a、b的值,在代入计算即可。
12.【答案】
【解析】【解答】解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠ABC=90°,
∵三角形ADE为正三角形,
∴AD=AE,∠EAD=60°,
∴∠BAE=150°,AB=AE,
∴∠ABE=∠AEB=15°,
∴ ,
故答案为: .
【分析】利用正方形的性质可证得AB=AD,∠BAD=∠ABC=90°,利用等边三角形的性质可证得AD=AE,∠EAD=60°;再利用等腰三角形的性质可求出∠ABE的度数,然后根据∠CBE=∠ABC-∠ABE,代入计算求出∠CBE的度数.
13.【答案】
【解析】【解答】解:∵∠BAC=∠BDC=90°,点O是BC的中点,
∴BC=2AO,OD=OB=OC,∠AOC=90°,
∴∠ODC=∠DCB,
∵BC=2AD,
∴AD=AO=OD,
∴△ADO是等边三角形,
∴∠AOD=60°,
∴∠DOC=90°-60°=30°,
∴∠DCB=(180°-30°)=75°.
故答案为:75°
【分析】利用直角三角形的性质可证得OB=OD=OC,利用等腰直角三角形的性质可知BC=2AO,∠AOC=90°,可推出AD=AO=OD,可得到△ADO是等边三角形,可求出∠AOD的度数,即可求出∠DOC的度数,利用等腰三角形的性质和三角形的内角和定理可求出∠DCB的度数.
14.【答案】
【解析】【解答】解:过B点作AC的对称点,由菱形对称性知刚好落在D处,连接DP,
则BP=DP,故BP+EP=DP+EP,
过D点作DH⊥AB于H点,
∴ 当E、P、D三点共线,且DE⊥AB时,由点到直线的距离垂线段最短知:
此时DP+EP有最小值,为DH长.
又四边形ABCD为菱形,DH⊥AB,
∴由菱形的等面积法知:AB×DH= ×AC×BD,且AB=5,代入数据:
∴ 5×DH= ×8×6,故DH= .
故答案为: .
【分析】利用菱形的性质可知点B,D关于AC对称,可得到DP=BP,利用垂线段最短可知 当E、P、D三点共线,且DE⊥AB时,DP+EP的最小值为DH的长;利用勾股定理求出菱形的边长,再利用菱形的两个面积公式可求出DH的长.
15.【答案】4
【解析】【解答】延长AP交BC于E,
∵AP垂直∠B的平分线BP于P,
∴∠ABP=∠EBP,∠APB=∠BPE=90°,
在△ABP和△EBP中,
∵ ,
∴△ABP≌△EPB(ASA),
∴S△ABP=S△BEP,AP=PE,
∴△APC和△CPE等底同高,
∴S△APC=S△PCE,
∵S△ABP=2S△APC,
∴S△BEP=2S△PCE,
∵S△PBC=6cm2,
∴S△BEP=4cm2,
∴S△ABP=4cm2.
故答案为:4
【分析】延长AP交BC于E,首先利用ASA判断出△ABP≌△EPB,根据全等三角形的性质得出S△ABP=S△BEP,AP=PE,根据等底同高的两个三角形的面积相等得出S△APC=S△PCE,然后由S△ABP=2S△APC,得出S△BEP=2S△PCE,再根据S△PBC=6cm2,即可算出答案。
16.【答案】
【解析】【解答】解:根据翻折的性质可得:
,
,且
,
,
,
,
又
四边形
是长方形,
,
,
,
故答案是:
.
【分析】根据翻折的性质可得
,由平角的定义可求出
,从而求出
,根据长方形的性质可得AD∥BC,利用平行线的性质可得
,继而得解.
17.【答案】110°或70°
【解析】【解答】①当点G在点F的右侧时,如图所示:
∵EN平分∠AEF,EM平分∠BEG,
∴∠NEF=∠AEF,∠MEG=∠BEG,
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB-∠FEG),
∵∠AEB=180°,∠FEG=40°,
∴∠NEF+∠MEG=(180°-40°)=70°,
∴∠MEN=∠NEF+∠FEG+∠MEG=70°+40°=110°;
②当点G在点F的左侧时,如图所示:
∵EN平分∠AEF,EM平分∠BEG,
∴∠NEF=∠AEF,∠MEG=∠BEG,
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB+∠FEG),
∵∠AEB=180°,∠FEG=40°,
∴∠NEF+∠MEG=(180°+40°)=110°,
∴∠MEN=∠NEF+∠MEG-∠FEG=110°-40°=70°;
综上,∠MEN的度数为110°或70°,
故答案为:110°或70°.
【分析】分类讨论:①当点G在点F的右侧时,②当点G在点F的左侧时,再分别画出图象并利用角平分线定义及角的运算求解即可.
18.【答案】4.8
【解析】【解答】解:过点C作CE⊥AB于点E,交AD于点P',再过点P'作P'Q'⊥AC于点Q',
∵AD平分∠BAC,CE⊥AB,P'Q'⊥AC,
∴P'E=P'Q',
∵CP'+P'Q'=CP'+P'E=CE,由垂线段最短可得CE最短,
∴当P点运动到P'位置,Q点运动到Q'点位置的时候,PC+PQ最小值等于CE,
∵S△ABC=×AC×BC=×AB×CE,
∴6×8=10×CE,
∴CE=4.8,
即PC+PQ的最小值等于4.8.
故答案为:4.8.
【分析】过点C作CE⊥AB于E,交AD于点P',再过点P'作P'Q'⊥AC于点Q',由角平分线上的点到角两边的距离相等得P'E=P'Q',进而根据线段的和差及等量代换得CP'+P'Q'=CP'+P'E=CE,由垂线段最短可得CE最短,故当P点运动到P'位置,Q点运动到Q'点位置的时候,PC+PQ最小值等于CE,从而由等面积法建立方程可求出CE的长,此题得解了.
19.【答案】(1)证明:∵∠B=90°,BC=3,AB=4,∴AC==5,∵CD=5,∴AC=CD.
(2)解:∵AC=CD=5 ,AD=,∴AC +CD =5 +5 =50,AD =,∴AC2+CD2=AD2,∴△ACD是直角三角形.
【解析】【分析】(1)根据勾股定理求出AC=5,即得AC=CD;
(2)根据勾股定理的逆定理进行解答即可.
20.【答案】解:如图,连接AE、AG,
∵D为AB中点,ED⊥AB,
∴EB=EA,
∴△ABE为等腰三角形,
又∵∠B= =30°,
∴∠BAE=30°,
∴∠AEG=60°,
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG,
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又BE+EG+GC=BC=15(cm),
∴EG=5(cm).
【解析】【分析】连接AE、AG,根据线段垂直平分线上的点到线段两端点的距离相等可得EB=EA,再根据等腰三角形两底角相等求出∠B,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEG=60°,同理求出∠AGE=60°,从而判断出,△AEG为等边三角形,再根据等边三角形三边都相等列式求解即可.
21.【答案】(1)( 1,2);( 2, 1);(2, 1)
(2)解:画图如下:
四边形ABCD的面积=4×3=12.
【解析】【分析】(1)根据点的坐标定义直接写出即可;
(2)根据平移的性质画图即可,由平移的性质可知四边形ABCD为平行四边形,则四边形ABCD的面积=底x高。
22.【答案】(1)证明:∵四边形为平行四边形,
∴.
在和中,
,
∴;
(2)证明:∵,
∴,
∴平行四边形是菱形.
【解析】【分析】(1)先根据平行四边形的性质得到,进而根据三角形全等的判定(AAS)即可求解;
(2)根据三角形全等的性质得到,进而根据菱形的判定即可求解。
23.【答案】(1)解:由折叠可得,∠ACE=∠DCE=∠ACD,∠BCF=∠B'CF=∠BCB',
又∵∠ACB=90°,
∴∠ACD+∠BCB'=90°,
∴∠ECD+∠FCD=×90°=45°,
即∠ECF=45°;
(2)解:由折叠可得:∠DEC=∠AEC=90°,BF=B'F=1,
∴∠EFC=45°=∠ECF,
∴CE=EF=4,
∴BE=4+1=5,
在Rt△BCE中,由勾股定理得:BC=
设AE=x,则AB=x+5,
∵Rt△ACE中,AC2=AE2+CE2,
Rt△ABC中,AC2=AB2-BC2,
∴AE2+CE2=AB2-BC2,
即x2+42=(x+5)2-41,
解得:x=,
∴AE=,AB=AE+BE=+5=
∴S△ABC=
【解析】【分析】⑴、由折叠(轴对称)知,三角形ACE和三角形DCE全等,三角形CBF全等于三角形B CF,所以∠ACE等于∠DCE,∠BCF等于∠B CF,故可知∠ECF等于二分之一的∠ACB,所以∠ECF可求;
⑵、由折叠知∠AEC等于∠DEC等于90度,且∠ECF等于45度,所以三角形ECF是等腰直角三角形,故EF等于EC等于4,所以EB等于5,直角三角形中由勾股定理可求CB长;三角形ABC是直角三角形且CB已经知道,所以求出AC的长,就可以求面积,利用共边直角三角形AEC和ACB,设 AE长从而建立方程求解,再求得AC长,从而求出三角形ABC的面积。
24.【答案】(1)解: 猜想:BE=FG;证明:过F作FG⊥DC,H为垂足,
则AB=AD=FH,∠FHG=∠BAE=90°,易证:∠GFH=∠ABE。
∴ΔFGH≌ΔBEA,∴BE=FG;
(2)证明: ∵ΔFGH≌ΔBEA,∴GH=AE;∵AF=DH,∴DG=DH+HG=AF+AE;
(3)
【解析】【分析】(1)根据题意结合图形可以猜想BE=FG,过点A作FG的平行线,构造平行四边形和全等三角形,即可证明BE=FG;
(2)由(1)的四边形AFGM是平行四边形,且 ΔFGH≌ΔBEA ,GH=AE;AF=DH,DG=DH+HG=AF+AE;
(3)过点C作CH⊥BE于点N,交AB于点H,先求得CH=FG=4,BH=AE=,再由勾股定理求得BC的长,根据相似三角形的性质求出CN的长即为点C到直线BE的距离。
25.【答案】(1)解:∵AE=BE,EF⊥AB,
∴FA=FB,
∴∠AFE=∠BFE=α,
∵∠DCB=∠ABC=∠FEB=90°,
∴∠EFC=90°,
∵BF⊥FG,
∴∠BFG=90°,
∴∠BFE=∠GFC=α,
∵∠DCA=45°,
∴∠G=45°-α.
(2)证明:∵∠OFC=90°,∠DCA=45°,
∴∠FOC=45°,FO=FC,
∴∠AOF=∠GCF=135°,
由(1)知:∠AFE=∠GFC,
∴△AOF≌△GCF(ASA).
∴AO=GC.
(3)解:连结OB,
∵AE=BE,OE⊥AB,
∴AO=BO,
∴∠OAB=∠OBA=45°,
∵BA=BC,
∴AO=CO=GC,
∵△AFG的面积为15,
∴△OFC的面积为5,
∴
∴,
∴CD=2FC=2.
【解析】【分析】(1)根据垂直平分线的性质得出∠AFE=∠BFE=α,再根据余角的性质求出∠BFE=∠GFC=α,然后根据三角形外角的性质求出∠G=45°-α,即可解答;
(2)先求出△OFC为等腰直角三角形,得出FO=FC,从而得出∠AOF=∠GCF,利用ASA证明△AOF≌△GCF,则可得出AO=GC;
(3)连接OB,根据垂直平分线的性质得出OA=OB,再根据直角三角形斜边中线的性质得出OA=OB,从而得出AO=CO=GC,再根据同底等高求出△OFC的面积为5,从而求出FC的长,则可求出CD长.
26.【答案】(1)解:、分别是、的平分线,
,,
,
,,
,
;
(2);
(3);
【解析】【解答】解:(2)①∠D与∠A之间的等量关系是:,理由如下:
∵ BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∵∠DBC +∠DCB +∠D= 180°,∠A+∠ABC+∠ACB= 180°,
∠ABC= 180°- 2∠DBC,∠ACB= 180°-2∠DCB,
∴∠A+ 180°- 2∠DBC+ 180° - 2∠DCB= 180°,∠DBC+∠DCB = 180° - ∠D,
∴∠A- 2(∠DBC+∠DCB)= -180°,
∴∠A- 2(180°-∠D)=- 180°,
∴∠A+ 2∠D= 180°,
∴
故答案为:,
②∠D与∠A之间的等量关系是:,理由如下:
∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠AC E的平分线,
∴∠DCE=∠DBC+∠D,∠A+ 2∠DBC = 2∠DCE,
∴∠A+ 2∠DBC= 2∠DBC+ 2∠D,
∴∠A= 2∠D,
∴,
(3)①由(1)可知:,
∵∠A=80°,
∴∠D=130°,
∴∠DBC+∠DCB=50°,
∴∠MBC+∠NCB=360°-50°=310°,
∵BE、CE分别平分∠MBC、∠NCB,
∴,
∴∠E=180°-155°=25°,
由(2)②可知:,
∴∠F=12.5°
故答案为:,
②由(2)②可知:,
∵∠F=n°,
∴∠E= 2∠F= 2n°
∵∠E+∠CBE+∠BCE= 180° ,
∴∠CBE+∠BCE= 180°-∠E= 180°- 2n°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠MBE=∠CBE,∠NCE=∠BCE,
∵∠MBC =∠MBE+ ∠CBE =2∠CBE,∠NCB=∠NCE+∠BCE= 2∠BCE,
∴∠MBC+∠NCB= 2(∠CBE +∠BCE) = 360° - 4n°,
∵∠DBC= 180°-∠MBC,∠DCB= 180°-∠NCB,
∴∠DBC+∠DCB= 180°-∠MBC +180° -∠NCB= 360°- (∠MBC+∠NCB) = 4n°,
∵∠DBC +∠DCB+∠D= 180°,
∴∠D= 180°- 4n°,
由(1)可知:,
∴∠A=180°-8n°,
故答案为:.
【分析】(1)利用角平分线的定义得出:,再利用三角形内角和定理即可求解;
(2)①利用三角形内角和定理可得:∠DBC+∠DCB +∠D= 180°,∠A+∠ABC+∠ACB= 180°, 利用角平分线的定义可得∠EBD=∠DBC,∠BCD=∠DCF,从而得到∠A-2(180°-∠D)= -180°,化简即可求;
②利用三角形的外角性质可得:∠DCE=∠DBC+∠D,∠A+ 2∠DBC= 2∠DCE,从而得到:∠A+2∠DBC= 2∠DBC+ 2∠D,化简即可求;
(3)①由(1) 知:,即可求出∠A,利用三角形内角和定理可得∠MBC +∠NCB,再利用角平分线的性质可得∠CBE +∠BCE,利用三角形内角和定理可得∠E,再由(2) ②可知,求解即可;
②利用(3) ①的解答过程进行逆推即可求解.
1 / 1
一、单选题(共10题,每小题3分,共30分)
1.如图,下列哪组条件不能判定四边形ABCD是平行四边形( )
A.AB∥CD,AB=CD B.AB∥CD,AD∥BC
C.OA=OC,OB=OD D.AB∥CD,AD=BC
2.下列几组数中,能作为直角三角形三边长度的是( )
A.1,1, B.2,3,4 C.3,4,5 D.5,7,9
3.下列多边形中,内角和与外角和相等的是( )
A.四边形 B.五边形 C.六边形 D.八边形
4.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( )
A.15 B.30 C.45 D.60
5.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1 B.4S2 C.4S2+S3 D.3S1+4S3
6.如果等边三角形的边长为3,那么连接各边中点所成的三角形的周长为( )
A.9 B.6 C.3 D.
7.如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E月;②分别以点E F为圆心,大于EF长为半径画弧,两弧相交于点G;③作射线AG交边BC于点D.则∠ADC的度数为( )
A.65° B.60° C.55° D.45°
8.把n边形变为 边形,内角和增加了720°,则x的值为( )
A.6 B.5 C.4 D.3
9.如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为(0,2),将△ABO沿着斜边AB翻折后得到△ABC,则点C的坐标是( )
A. B. C. D.
10.如图,等边三角形ABC的边长为2,点O是△ABC的中心,∠FOG=120°,将∠FOG绕点O旋转,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:①OD=OE;②S四边形ODBE= S△ABC;③S△ODE=S△BDE;④△BDE周长的最小值为3.上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共8题,每小题3分,共24分)
11.已知点P(2,﹣3)与点Q(a,b)关于原点对称,则a+b= .
12.如图,在正方形ABCD的外侧,作等边 ,连接BE、CE, 的度数是 .
13.如图,在四边形中,O是中点,,,若,则 .
14.如图,菱形 的对角线交于点 是线段 上一动点, E 是线段 AB上一个动点,则 的最小值为 .
15.如图,△ABC中,AP垂直∠B的平分线BP于P.若△PBC的面积为6cm2,且△APB的面积是△APC的面积的2倍.则△APB的面积= cm2.
16.如图,将长方形沿翻折,点的对应点恰好落在边上,若,则的度数为 .
17.如图,长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG,将∠BEG对折,点B落在直线EG上的点B'处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A'处,得折痕EN.∠FEG=40°,则∠MEN= .
18.如图,在中,,,,,是的平分线.若,分别是和上的动点,则的最小值是 .
三、解答题(共8题,第19-23题每题6分,第24-26每题12分)
19.如图,连接四边形ABCD的对角线AC,已知∠B=90°,BC=3,AB=4,CD=5,AD=.
求证:
(1)AC=CD;
(2)△ACD是直角三角形.
20.△ABC中,AB=AC,∠BAC=120°,点D、F分别为AB、AC中点,ED⊥AB,GF⊥AC,若BC=15cm,求EG的长.
21.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点、、均在格点上.
(1)请直接写出点、、的坐标分别为 , , .
(2)若平移线段,使移动到的位置,请在图中画出移动后的位置,依次连接,,,,则四边形的面积为 ▲ .
22.nbsp;.如图,在ABCD平行四边形中,过点A作于点E,于点F,.求证:
(1);
(2)四边形ABCD是菱形.
23.如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,
(1)求∠ECF的度数;
(2)若CE=4,B′F=1,求线段BC的长和△ABC的面积.
24.在正方形ABCD中,点E,F,G分别在边AD,AB,CD上(点E、F、G不与正方形的顶点重合),BE,FG相交于点O,且FG⊥BE.
(1)猜想BE与FG的数量关系并证明;
(2)证明:DG=AF+AE;
(3)若AE= ,FG=4,请直接写出点C到直线BE的距离;
25.如图,四边形ABCD为正方形,E为AB的中点,作EF⊥AB交CD于F,连结AF,BF,作FG⊥BF交AC的延长线于G,AC与EF交于点O.
(1)设∠AFE=α,用含a的代数式表示∠G的度数.
(2)求证:AO=GC.
(3)如图,若△AFG的面积为15,求正方形ABCD的边长.
26.
(1)【情景引入】:
如图,、分别是的内角、的平分线,说明的理由.
(2)【深入探究】:
如图,、分别是的两个外角、的平分线,与之间的等量关系是 ;
如图,、分别是的一个内角和一个外角的平分线,与之间的等量关系是 .
(3)【拓展应用】:
请用以上结论解决下列问题:如图,在中,、分别平分、,、、分别在、、的延长线上,、分别平分、,、分别平分、.
,则的度数为 ;
,则的度数为 .
答案解析部分
1.【答案】D
【解析】【解答】根据平行四边形的判定,A、B、C均符合是平行四边形的条件,D则不能判定是平行四边形.
故答案为:D.
【分析】A.一组对边平行且相等是四边形是平行四边形;
B.两组边分别平行的四边形是平行四边形;
C.对角线互相平分的四边形是平行四边形;
D.一组对边平行,另一组对边相等的四边形不能判定为平行四边形,也可能是等腰梯形。
2.【答案】C
【解析】【解答】解:A、12+12≠( )2,故不是直角三角形,故此选项错误;
B、22+32≠42,故不是直角三角形,故此选项错误;
C、32+42=52,故是直角三角形,故此选项正确;
D、52+72≠92,故不是直角三角形,故此选项错误.
故答案为:C.
【分析】若一个三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形为直角三角形,据此判断.
3.【答案】A
【解析】【解答】解:设多边形的边数是n,则(n﹣2) 180=360,
解得n=4.
故选A.
【分析】设多边形的边数是n,根据多边形的内角和定理即可求解.
4.【答案】B
【解析】【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积= ×AB×DE=30,
故答案为:B.
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC=4,根据三角形的面积公式计算即可.
5.【答案】A
【解析】【解答】解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2= (a+c)(a﹣c)= a2﹣ c2,
∴S2=S1﹣ S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选A.
【分析】设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S1,S2,S3之间的关系,由此即可解决问题.
6.【答案】D
【解析】【解答】解:连接各边中点所成的线段是等边三角形的中位线,每条中位线的长是 ,故新成的三角形的周长为 ×3= .
故选D
【分析】等边三角形的边长为3,根据三角形的中位线定理可求出中点三角形的边长,所以中点三角形的周长可求解.
7.【答案】A
【解析】【解答】解:由作图可得:
AG是∠CAB的角平分线
∵∠CAB=50°
∴
在△ADC中,∠C=90°
∴∠ADC=180°-∠C-∠CAD=65°
故答案为:A
【分析】根据作图可知AG是∠CAB的角平分线,再根据角平分线性质可得,再根据三角形内角和定理即可求出答案.
8.【答案】C
【解析】【解答】把n边形变为(n+x)边形,内角和增加了720°,
根据内角和公式得
(n+x-2)×180°-(n-2)×180°=720°,
解得x=4,
故答案为:C.
【分析】根据内角和公式列出方程即可求解.
9.【答案】C
【解析】【解答】解: , , ,
, ,
过点C作 轴,垂直为D,则 .
, .
.
故答案为:C
【分析】先根据轴对称的性质可得△BOA≌△BCA,即可得出OB=BC=2, ∠CBA=∠OBA=60°,然后过点C作垂线,可得∠DCB=30°,根据直角三角形的性质可得DB,DC,从而得出点的坐标.
10.【答案】C
【解析】【解答】连接OB、OC,如图,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点O是△ABC的中心,
∴OB=OC,OB、OC分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=∠OCB=30°,
∴∠BOC=120°,即∠BOE+∠COE=120°,
而∠DOE=120°,即∠BOE+∠BOD=120°,
∴∠BOD=∠COE,
在△BOD和△COE中,
,
∴△BOD≌△COE(ASA),
∴BD=CE,OD=OE,
∴①符合题意;
∵△BOD≌△COE,
∴S△BOD=S△COE,
∴四边形ODBE的面积=S△OBC═ S△ABC,
故②符合题意;
作OH⊥DE于H,如图,则DH=EH,
∵∠DOE=120°,
∴∠ODE=∠OEH=30°,
∴OH= OE,HE= OH= OE,
∴DE= OE,
∴S△ODE= × OE× OE= OE2,
即S△ODE随OE的变化而变化,
而四边形ODBE的面积为定值,
∴S△ODE≠S△BDE;
故③不符合题意;
∵BD=CE,
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=2+DE=2+ OE,
当OE⊥BC时,OE最小,△BDE的周长最小,此时OE= ,
∴△BDE周长的最小值=2+1=3,
故④符合题意.
综上所述,正确的有①②④共3个.
故答案为:C.
【分析】利用旋转的性质,再结合三角形全等的判定和性质逐项判定即可。
11.【答案】1
【解析】【解答】解:∵点与点关于原点对称,
∴a=-2,b= 3,
∴a+b=-2+3=1,
故答案为:1.
【分析】关于原点对称的坐标特征得出a、b的值,在代入计算即可。
12.【答案】
【解析】【解答】解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠ABC=90°,
∵三角形ADE为正三角形,
∴AD=AE,∠EAD=60°,
∴∠BAE=150°,AB=AE,
∴∠ABE=∠AEB=15°,
∴ ,
故答案为: .
【分析】利用正方形的性质可证得AB=AD,∠BAD=∠ABC=90°,利用等边三角形的性质可证得AD=AE,∠EAD=60°;再利用等腰三角形的性质可求出∠ABE的度数,然后根据∠CBE=∠ABC-∠ABE,代入计算求出∠CBE的度数.
13.【答案】
【解析】【解答】解:∵∠BAC=∠BDC=90°,点O是BC的中点,
∴BC=2AO,OD=OB=OC,∠AOC=90°,
∴∠ODC=∠DCB,
∵BC=2AD,
∴AD=AO=OD,
∴△ADO是等边三角形,
∴∠AOD=60°,
∴∠DOC=90°-60°=30°,
∴∠DCB=(180°-30°)=75°.
故答案为:75°
【分析】利用直角三角形的性质可证得OB=OD=OC,利用等腰直角三角形的性质可知BC=2AO,∠AOC=90°,可推出AD=AO=OD,可得到△ADO是等边三角形,可求出∠AOD的度数,即可求出∠DOC的度数,利用等腰三角形的性质和三角形的内角和定理可求出∠DCB的度数.
14.【答案】
【解析】【解答】解:过B点作AC的对称点,由菱形对称性知刚好落在D处,连接DP,
则BP=DP,故BP+EP=DP+EP,
过D点作DH⊥AB于H点,
∴ 当E、P、D三点共线,且DE⊥AB时,由点到直线的距离垂线段最短知:
此时DP+EP有最小值,为DH长.
又四边形ABCD为菱形,DH⊥AB,
∴由菱形的等面积法知:AB×DH= ×AC×BD,且AB=5,代入数据:
∴ 5×DH= ×8×6,故DH= .
故答案为: .
【分析】利用菱形的性质可知点B,D关于AC对称,可得到DP=BP,利用垂线段最短可知 当E、P、D三点共线,且DE⊥AB时,DP+EP的最小值为DH的长;利用勾股定理求出菱形的边长,再利用菱形的两个面积公式可求出DH的长.
15.【答案】4
【解析】【解答】延长AP交BC于E,
∵AP垂直∠B的平分线BP于P,
∴∠ABP=∠EBP,∠APB=∠BPE=90°,
在△ABP和△EBP中,
∵ ,
∴△ABP≌△EPB(ASA),
∴S△ABP=S△BEP,AP=PE,
∴△APC和△CPE等底同高,
∴S△APC=S△PCE,
∵S△ABP=2S△APC,
∴S△BEP=2S△PCE,
∵S△PBC=6cm2,
∴S△BEP=4cm2,
∴S△ABP=4cm2.
故答案为:4
【分析】延长AP交BC于E,首先利用ASA判断出△ABP≌△EPB,根据全等三角形的性质得出S△ABP=S△BEP,AP=PE,根据等底同高的两个三角形的面积相等得出S△APC=S△PCE,然后由S△ABP=2S△APC,得出S△BEP=2S△PCE,再根据S△PBC=6cm2,即可算出答案。
16.【答案】
【解析】【解答】解:根据翻折的性质可得:
,
,且
,
,
,
,
又
四边形
是长方形,
,
,
,
故答案是:
.
【分析】根据翻折的性质可得
,由平角的定义可求出
,从而求出
,根据长方形的性质可得AD∥BC,利用平行线的性质可得
,继而得解.
17.【答案】110°或70°
【解析】【解答】①当点G在点F的右侧时,如图所示:
∵EN平分∠AEF,EM平分∠BEG,
∴∠NEF=∠AEF,∠MEG=∠BEG,
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB-∠FEG),
∵∠AEB=180°,∠FEG=40°,
∴∠NEF+∠MEG=(180°-40°)=70°,
∴∠MEN=∠NEF+∠FEG+∠MEG=70°+40°=110°;
②当点G在点F的左侧时,如图所示:
∵EN平分∠AEF,EM平分∠BEG,
∴∠NEF=∠AEF,∠MEG=∠BEG,
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB+∠FEG),
∵∠AEB=180°,∠FEG=40°,
∴∠NEF+∠MEG=(180°+40°)=110°,
∴∠MEN=∠NEF+∠MEG-∠FEG=110°-40°=70°;
综上,∠MEN的度数为110°或70°,
故答案为:110°或70°.
【分析】分类讨论:①当点G在点F的右侧时,②当点G在点F的左侧时,再分别画出图象并利用角平分线定义及角的运算求解即可.
18.【答案】4.8
【解析】【解答】解:过点C作CE⊥AB于点E,交AD于点P',再过点P'作P'Q'⊥AC于点Q',
∵AD平分∠BAC,CE⊥AB,P'Q'⊥AC,
∴P'E=P'Q',
∵CP'+P'Q'=CP'+P'E=CE,由垂线段最短可得CE最短,
∴当P点运动到P'位置,Q点运动到Q'点位置的时候,PC+PQ最小值等于CE,
∵S△ABC=×AC×BC=×AB×CE,
∴6×8=10×CE,
∴CE=4.8,
即PC+PQ的最小值等于4.8.
故答案为:4.8.
【分析】过点C作CE⊥AB于E,交AD于点P',再过点P'作P'Q'⊥AC于点Q',由角平分线上的点到角两边的距离相等得P'E=P'Q',进而根据线段的和差及等量代换得CP'+P'Q'=CP'+P'E=CE,由垂线段最短可得CE最短,故当P点运动到P'位置,Q点运动到Q'点位置的时候,PC+PQ最小值等于CE,从而由等面积法建立方程可求出CE的长,此题得解了.
19.【答案】(1)证明:∵∠B=90°,BC=3,AB=4,∴AC==5,∵CD=5,∴AC=CD.
(2)解:∵AC=CD=5 ,AD=,∴AC +CD =5 +5 =50,AD =,∴AC2+CD2=AD2,∴△ACD是直角三角形.
【解析】【分析】(1)根据勾股定理求出AC=5,即得AC=CD;
(2)根据勾股定理的逆定理进行解答即可.
20.【答案】解:如图,连接AE、AG,
∵D为AB中点,ED⊥AB,
∴EB=EA,
∴△ABE为等腰三角形,
又∵∠B= =30°,
∴∠BAE=30°,
∴∠AEG=60°,
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG,
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又BE+EG+GC=BC=15(cm),
∴EG=5(cm).
【解析】【分析】连接AE、AG,根据线段垂直平分线上的点到线段两端点的距离相等可得EB=EA,再根据等腰三角形两底角相等求出∠B,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEG=60°,同理求出∠AGE=60°,从而判断出,△AEG为等边三角形,再根据等边三角形三边都相等列式求解即可.
21.【答案】(1)( 1,2);( 2, 1);(2, 1)
(2)解:画图如下:
四边形ABCD的面积=4×3=12.
【解析】【分析】(1)根据点的坐标定义直接写出即可;
(2)根据平移的性质画图即可,由平移的性质可知四边形ABCD为平行四边形,则四边形ABCD的面积=底x高。
22.【答案】(1)证明:∵四边形为平行四边形,
∴.
在和中,
,
∴;
(2)证明:∵,
∴,
∴平行四边形是菱形.
【解析】【分析】(1)先根据平行四边形的性质得到,进而根据三角形全等的判定(AAS)即可求解;
(2)根据三角形全等的性质得到,进而根据菱形的判定即可求解。
23.【答案】(1)解:由折叠可得,∠ACE=∠DCE=∠ACD,∠BCF=∠B'CF=∠BCB',
又∵∠ACB=90°,
∴∠ACD+∠BCB'=90°,
∴∠ECD+∠FCD=×90°=45°,
即∠ECF=45°;
(2)解:由折叠可得:∠DEC=∠AEC=90°,BF=B'F=1,
∴∠EFC=45°=∠ECF,
∴CE=EF=4,
∴BE=4+1=5,
在Rt△BCE中,由勾股定理得:BC=
设AE=x,则AB=x+5,
∵Rt△ACE中,AC2=AE2+CE2,
Rt△ABC中,AC2=AB2-BC2,
∴AE2+CE2=AB2-BC2,
即x2+42=(x+5)2-41,
解得:x=,
∴AE=,AB=AE+BE=+5=
∴S△ABC=
【解析】【分析】⑴、由折叠(轴对称)知,三角形ACE和三角形DCE全等,三角形CBF全等于三角形B CF,所以∠ACE等于∠DCE,∠BCF等于∠B CF,故可知∠ECF等于二分之一的∠ACB,所以∠ECF可求;
⑵、由折叠知∠AEC等于∠DEC等于90度,且∠ECF等于45度,所以三角形ECF是等腰直角三角形,故EF等于EC等于4,所以EB等于5,直角三角形中由勾股定理可求CB长;三角形ABC是直角三角形且CB已经知道,所以求出AC的长,就可以求面积,利用共边直角三角形AEC和ACB,设 AE长从而建立方程求解,再求得AC长,从而求出三角形ABC的面积。
24.【答案】(1)解: 猜想:BE=FG;证明:过F作FG⊥DC,H为垂足,
则AB=AD=FH,∠FHG=∠BAE=90°,易证:∠GFH=∠ABE。
∴ΔFGH≌ΔBEA,∴BE=FG;
(2)证明: ∵ΔFGH≌ΔBEA,∴GH=AE;∵AF=DH,∴DG=DH+HG=AF+AE;
(3)
【解析】【分析】(1)根据题意结合图形可以猜想BE=FG,过点A作FG的平行线,构造平行四边形和全等三角形,即可证明BE=FG;
(2)由(1)的四边形AFGM是平行四边形,且 ΔFGH≌ΔBEA ,GH=AE;AF=DH,DG=DH+HG=AF+AE;
(3)过点C作CH⊥BE于点N,交AB于点H,先求得CH=FG=4,BH=AE=,再由勾股定理求得BC的长,根据相似三角形的性质求出CN的长即为点C到直线BE的距离。
25.【答案】(1)解:∵AE=BE,EF⊥AB,
∴FA=FB,
∴∠AFE=∠BFE=α,
∵∠DCB=∠ABC=∠FEB=90°,
∴∠EFC=90°,
∵BF⊥FG,
∴∠BFG=90°,
∴∠BFE=∠GFC=α,
∵∠DCA=45°,
∴∠G=45°-α.
(2)证明:∵∠OFC=90°,∠DCA=45°,
∴∠FOC=45°,FO=FC,
∴∠AOF=∠GCF=135°,
由(1)知:∠AFE=∠GFC,
∴△AOF≌△GCF(ASA).
∴AO=GC.
(3)解:连结OB,
∵AE=BE,OE⊥AB,
∴AO=BO,
∴∠OAB=∠OBA=45°,
∵BA=BC,
∴AO=CO=GC,
∵△AFG的面积为15,
∴△OFC的面积为5,
∴
∴,
∴CD=2FC=2.
【解析】【分析】(1)根据垂直平分线的性质得出∠AFE=∠BFE=α,再根据余角的性质求出∠BFE=∠GFC=α,然后根据三角形外角的性质求出∠G=45°-α,即可解答;
(2)先求出△OFC为等腰直角三角形,得出FO=FC,从而得出∠AOF=∠GCF,利用ASA证明△AOF≌△GCF,则可得出AO=GC;
(3)连接OB,根据垂直平分线的性质得出OA=OB,再根据直角三角形斜边中线的性质得出OA=OB,从而得出AO=CO=GC,再根据同底等高求出△OFC的面积为5,从而求出FC的长,则可求出CD长.
26.【答案】(1)解:、分别是、的平分线,
,,
,
,,
,
;
(2);
(3);
【解析】【解答】解:(2)①∠D与∠A之间的等量关系是:,理由如下:
∵ BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∵∠DBC +∠DCB +∠D= 180°,∠A+∠ABC+∠ACB= 180°,
∠ABC= 180°- 2∠DBC,∠ACB= 180°-2∠DCB,
∴∠A+ 180°- 2∠DBC+ 180° - 2∠DCB= 180°,∠DBC+∠DCB = 180° - ∠D,
∴∠A- 2(∠DBC+∠DCB)= -180°,
∴∠A- 2(180°-∠D)=- 180°,
∴∠A+ 2∠D= 180°,
∴
故答案为:,
②∠D与∠A之间的等量关系是:,理由如下:
∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠AC E的平分线,
∴∠DCE=∠DBC+∠D,∠A+ 2∠DBC = 2∠DCE,
∴∠A+ 2∠DBC= 2∠DBC+ 2∠D,
∴∠A= 2∠D,
∴,
(3)①由(1)可知:,
∵∠A=80°,
∴∠D=130°,
∴∠DBC+∠DCB=50°,
∴∠MBC+∠NCB=360°-50°=310°,
∵BE、CE分别平分∠MBC、∠NCB,
∴,
∴∠E=180°-155°=25°,
由(2)②可知:,
∴∠F=12.5°
故答案为:,
②由(2)②可知:,
∵∠F=n°,
∴∠E= 2∠F= 2n°
∵∠E+∠CBE+∠BCE= 180° ,
∴∠CBE+∠BCE= 180°-∠E= 180°- 2n°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠MBE=∠CBE,∠NCE=∠BCE,
∵∠MBC =∠MBE+ ∠CBE =2∠CBE,∠NCB=∠NCE+∠BCE= 2∠BCE,
∴∠MBC+∠NCB= 2(∠CBE +∠BCE) = 360° - 4n°,
∵∠DBC= 180°-∠MBC,∠DCB= 180°-∠NCB,
∴∠DBC+∠DCB= 180°-∠MBC +180° -∠NCB= 360°- (∠MBC+∠NCB) = 4n°,
∵∠DBC +∠DCB+∠D= 180°,
∴∠D= 180°- 4n°,
由(1)可知:,
∴∠A=180°-8n°,
故答案为:.
【分析】(1)利用角平分线的定义得出:,再利用三角形内角和定理即可求解;
(2)①利用三角形内角和定理可得:∠DBC+∠DCB +∠D= 180°,∠A+∠ABC+∠ACB= 180°, 利用角平分线的定义可得∠EBD=∠DBC,∠BCD=∠DCF,从而得到∠A-2(180°-∠D)= -180°,化简即可求;
②利用三角形的外角性质可得:∠DCE=∠DBC+∠D,∠A+ 2∠DBC= 2∠DCE,从而得到:∠A+2∠DBC= 2∠DBC+ 2∠D,化简即可求;
(3)①由(1) 知:,即可求出∠A,利用三角形内角和定理可得∠MBC +∠NCB,再利用角平分线的性质可得∠CBE +∠BCE,利用三角形内角和定理可得∠E,再由(2) ②可知,求解即可;
②利用(3) ①的解答过程进行逆推即可求解.
1 / 1
同课章节目录
