2024辽宁中考数学二轮专题复习 微专题 二次函数与直角三角形问题(41张PPT)
文档属性
| 名称 | 2024辽宁中考数学二轮专题复习 微专题 二次函数与直角三角形问题(41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 00:00:00 | ||
图片预览









文档简介
(共41张PPT)
微专题 二次函数与直角三角形问题
例1题图
微技能——分类讨论思想确定动点位置
一阶
例1 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C.连接AC.
一题多设问
探究1:在抛物线对称轴上找一点P使得△ACP为直角三
角形.
例1题图①
(1)若AC为斜边时,∠APC=90°;在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例1 探究1:(1)满足条件的点P如解图①
例1题解图①
【作图依据】__________________________
直径所对圆周角等于90°.
例1题图②
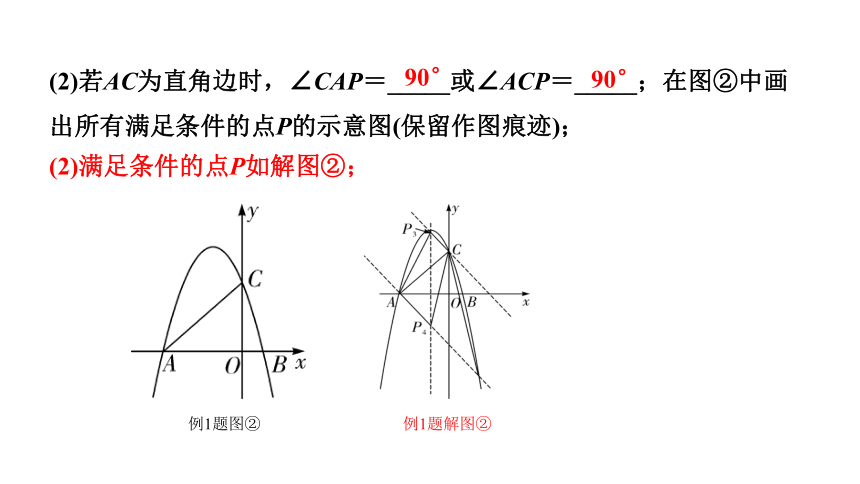
(2)若AC为直角边时,∠CAP=_____或∠ACP=_____;在图②中画出所有满足条件的点P的示意图(保留作图痕迹);
90°
90°
(2)满足条件的点P如解图②;
例1题解图②
例1题图③
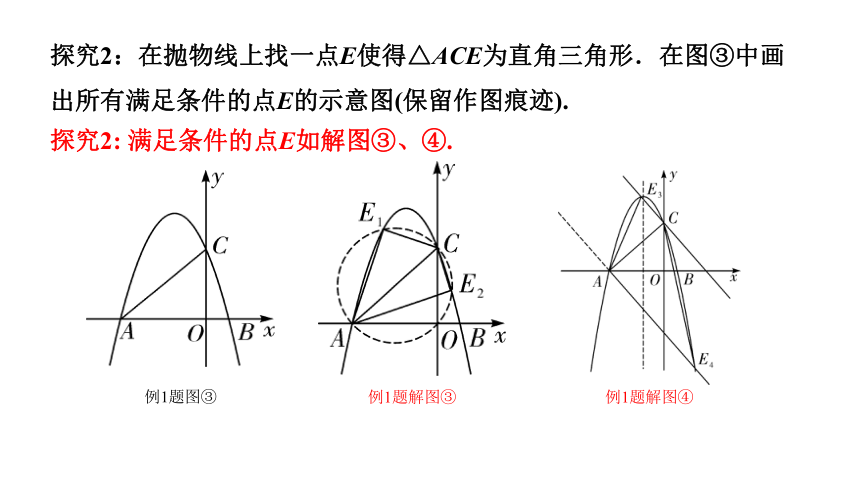
探究2:在抛物线上找一点E使得△ACE为直角三角形.在图③中画出所有满足条件的点E的示意图(保留作图痕迹).
探究2: 满足条件的点E如解图③、④.
例1题解图③
例1题解图④
【方法总结】二次函数中直角三角形的存在性一般要分情况讨论:常以已知边为_____或________讨论;以自主探究1为例,已知边AC为斜边时,可以作以斜边AC为直径的圆,作图方法为:_______________,所找点即为___________的交点;若已知边AC为直角边时,作图方法为:_____________________________,所找点即为_____________的交点.
斜边
直角边
以AC为直径画圆
圆与对称轴
分别过点A,C作线段AC的垂线
垂线与对称轴
【思考】若动点在y轴上、x轴上时,确定动点位置有什么不同呢?
一题多设问
二阶
一题多设问
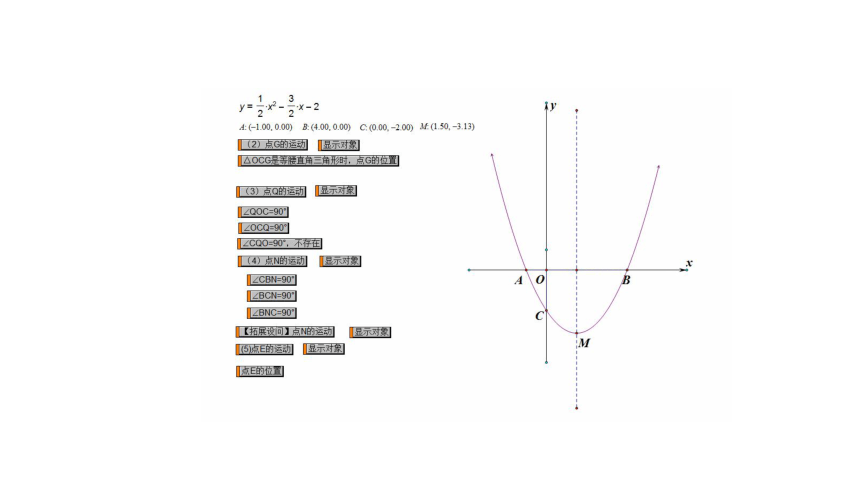
例2 如图,已知抛物线y= x2- x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,对称轴为直线l,顶点为M.
例2题图①
(1)求点A,B的坐标及抛物线的对称轴;
例2 解:(1)令y= x2- x-2=0,解得x1=-1,x2=4,
∵点A在点B的左侧,
∴点A的坐标为(-1,0),点B的坐标为(4,0).
∴抛物线的对称轴为直线x= ;
例2题图①
例2题图②
(2)若点G是x轴上一点,当△OCG为等腰直角三角形时,请直接写出点G的坐标;
【思维教练】由于点G在x轴上,可知∠COG=90°,要让它为等腰直角三角形,则需要分为当点G在x正半轴和负半轴两种情况讨论.
【解法提示】由题意知,点C的坐标为(0,-2).∴OC=2.
∵点G在x轴上,
∴当△OCG为等腰直角三角形时,
分点G在x轴正半轴和负半轴两种情况讨论:
①当点G在x轴正半轴时,
∵OC=OG,∴OG=2.
∴点G的坐标为(2,0);
②当点G在x轴负半轴时,
∵OC=OG,∴OG=2.
∴点G的坐标为(-2,0).
综上所述,满足条件的点G的坐标为(2,0)或(-2,0);
(2)点G的坐标为(2,0)或(-2,0);
例2题图②
例2题解图
(3)抛物线对称轴上是否存在点Q,使得△OCQ是以OC为直角边的直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由;
【思维教练】△OCQ是以OC为直角边的直角三角形,所以需分点O为直角顶点和点C为直角顶点两种情况讨论,进而求解.
【解法提示】如解图,∵点Q在抛物线的对称轴上,
∴设点Q的坐标为( ,q),
∵△COQ是以CO为直角边的直角三角形,
∴当∠COQ=90°时,点Q是对称轴与x轴的交点,
此时点Q的坐标为( ,0);当∠OCQ=90°时,CQ∥x轴,
∴点Q的坐标为( ,-2).
综上所述,满足条件的点Q的坐标为( ,0)或( ,-2);
(3)存在,点Q的坐标为( ,0)或( ,-2);
例2题解图
例2题图④
(4)若点N是对称轴上一点,是否存在点N使得△NBC是直角三角形,若存在,请直接写出点N的纵坐标;若不存在,请说明理由;
【思维教练】点N是对称轴l上一点,当△NBC是直角三角形时,需分∠NCB,∠NBC,∠BNC为直角时三种情况进行讨论,进而求解.
【解法提示】设点N的坐标为( ,t),
则CN2=( )2+(2+t)2,BN2=(4- )2+t2,BC2=20,
当△NBC是直角三角形时,分以下三种情况:
①当∠NCB=90°时,NC2+BC2=NB2,
即( )2+(2+t)2+20=(4- )2+t2,解得t=-5;
②当∠NBC=90°时,NB2+BC2=NC2,
即(4- )2+t2+20=( )2+(2+t)2,
解得t=5;
③当∠BNC=90°时,NB2+NC2=BC2,
即(4- )2+t2+( )2+(2+t)2=20,
解得t= 或 .
综上所述,当△NBC是直角三角形时,点N的纵坐标为-5或5或 或 ;
(4)存在.点N的纵坐标为-5或5或 或 ;
例2题图④
【拓展设问】点N是对称轴上一点,若△NBC是锐角三角形时,请直接写出点N的纵坐标n的取值范围.
【思考】若△NBC是钝角三角形时,点N的纵坐标n的取值范围是什么.
【拓展设问】由(4)知,当∠NCB=90°时,t=-5,当∠NBC=90°时,t=5,当∠BNC=90°时,t= 或t= ,
结合图象可知,当△NBC是锐角三角形时,点N的纵坐标n的取值范围是-5<n< 或 <n<5;
【思考】同理可得当△NBC是钝角三角形时,点N的纵坐标n的取值范围是n<-5或 <n< 或n>5.
例2题图⑤
(5)点D是y轴上一点,其坐标为(0,4).动点E是直线BD上一点,过点E作EF⊥BD,交y轴于点F,连接AF,BF,若△ABF是直角三角形,试求点E的坐标.
【思维教练】点F在y轴上,所以当△ABF是直角三角形时,∠FAB和∠FBA不可能是直角,所以只能是∠AFB为直角,
当∠AFB为直角时,注意要分点F在y轴的正、负半轴
两种情况讨论.
(5)∵点D在y轴上,且点D的坐标为(0,4),点B的坐标为(4,0),
∴直线BD的函数表达式为y=-x+4,
∵点E是直线y=-x+4上一点,
∴设点E的坐标为(m,-m+4),
∵EF⊥BD,
∴易得直线EF的函数表达式为y=x-2m+4.
∴点F的坐标为(0,-2m+4).
∴AF2=12+(-2m+4)2,BF2=42+(-2m+4)2,AB2=52=25.
例2题图⑤
∵点F在y轴上,
∴只能有∠AFB=90°.即AF2+BF2=AB2.
即12+(-2m+4)2+42+(-2m+4)2=25.
解得m=1或3.
当m=1时,点E的坐标为(1,3);
当m=3时,点E的坐标为(3,1).
综上所述,当△ABF是直角三角形时,点E的坐标为(1,3)或(3,1).
例2题图⑤
综合训练
三阶
第1题图
1.如图,在平面直角坐标系中,抛物线y=-x2+bx+c的图象与坐标轴相交于A、B、C三点,其中A点坐标为(3,0),B点坐标为(-1,0),连接AC、BC.动点P从点A出发,在线段AC上以每 秒个单位长度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
(1)求b、c的值.
解:(1)∵抛物线y=-x2+bx+c经过点A(3,0),B(-1,0),
则 ,解得
第1题图
第1题图
(2)在P、Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?
(2)由(1)得,抛物线表达式为y=-x2+2x+3,C(0,3),A(3,0),
∴△OAC是等腰直角三角形,由点P的运动可知AP= t,
如解图,过点P作PE⊥x轴,垂足为E,
∴AE=PE= =t,即E(3-t,0),
E
∟
= ×4×3- ×[3-(-1+t)]t= t2-2t+6,
∵当其中一点到达终点时,另一点随之停止运动,
AC= ,AB=4,
∴0≤t≤3,
∵ >0,∴当t=2时,四边形BCPQ的面积最小,
最小值为 ×22-2×2+6=4;
E
∟
又Q(-1+t,0),
∴S四边形BCPQ=S△ABC-S△APQ
第1题图
(3)在线段AC上方的抛物线上是否存在点M,使△MPQ是以点P为直角顶点的等腰直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
(3)存在点M,使△MPQ是以点P为直角顶点的等腰直角三角形.
理由如下:
∵点M是线段AC上方的抛物线上的点,
第1题解图②
如解图②,过点P作x轴的垂线,交x轴于点E,
过M作EP的垂线交EP的延长线于点F,
∵△PMQ是等腰直角三角形,PM=PQ,∠MPQ=90°,
∴∠MPF+∠QPE=90°,又∠MPF+∠PMF=90°,
∴∠PMF=∠QPE,
在△PFM和△QEP中,
∴△PFM≌△QEP(AAS),
第1题解图②
∴MF=PE=t,PF=QE=4-2t,
∴EF=4-2t+t=4-t,
∴点M的坐标为(3-2t,4-t),
∵点M在抛物线y=-x2+2x+3上,
∴4-t=-(3-2t)2+2(3-2t)+3,
解得t= 或 (舍去),
∴点M的坐标为( , ).
第1题解图②
第2题图
2.已知抛物线y=ax2+bx+c与x轴交于A(-2,0)、B(6,0)两点,与y轴交于点C(0,-3).
(1)求抛物线的表达式;
解:(1)设抛物线的表达式为y=a(x+2)(x-6),
把点C(0,-3)代入,得-3=a(0+2)(0-6),
解得a= ,
∴抛物线的表达式为:
y= (x+2)(x-6)= x2-x-3;
第2题图
(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当 最大时,求点P的坐标及 的最大值;
设点P的坐标为(n, n2-n-3)(0<n<6),则OE=n,
设直线AP的解析式为y=kx+b(k≠0),
根据题意得 解得
(2)如解图,过点P作PE⊥x轴于点E,过点M作MF⊥x轴于点F,
则MF∥PE,
F
∟
E
∟
∴直线AP的解析式为y= (n-6)x+ (n-6),
设直线BC的解析式为y=mx+a(m≠0),
根据题意得 解得
,
∴直线BC的解析式为y= x-3,
联立直线AP和BC的解析式
得 解得
第2题图
F
∟
E
∟
即点M的坐标为( , ),则OF= ,
∴EF= = ,AF= ,
又∵MF∥PE,
∴
,
∴
第2题图
F
∟
E
∟
∵ <0,0<n<6,
∴当n=3时, 有最大值,最大值为 ,
此时点P的坐标为(3, ), 的最大值为 .
第2题图
F
∟
E
∟
第2题图
(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使△BCD是直角三角形,若存在,请直接写出点D的坐标;若不存在,请说明理由.
【解法提示】设点D的坐标为(3,m),∵B(6,0),C(0,-3),
∴BD2=m2+9,CD2=(m+3)2+9,BC2=45,
①当∠BCD=90°时,有BD2=CD2+BC2,
∴m2+9=(m+3)2+9+45,
整理得:6m=-54,解得m=-9,
∴点D的坐标为(3,-9);
②当∠BDC=90°时,有BC2=BD2+CD2,
∴45=m2+9+(m+3)2+9,整理得.m2+3m-9=0
解得m1= ,m2= ,
∴点D的坐标为(3, )或(3, );
③当∠CBD=90°时,有CD2=BC2+BD2,
∴(m+3)2+9=45+m2+9,
解得m=6,
∴点D的坐标为(3,6);
第2题图
综上所述,满足条件的点D坐标为(3,-9)或(3,6)或(3, )或(3, ).
(3)存在点D,使△BCD是直角三角形,点D的坐标为(3,-9)或(3,6)或(3, )或(3, ).
第2题图
备用图
3.如图,抛物线y=- x2+bx+c与x轴交于点A和点C(-1,0),与y轴交于点B(0,3),连接AB,BC,点P是抛物线第一象限上的一动点,过点P作PD⊥x轴于点D,交AB于点E.
第3题图
(1)求抛物线的解析式;
解:(1)∵抛物线y=- x2+bx+c经过C(-1,0),B(0,3)两点,
∴ ,解得
∴抛物线的解析式为:
;
第3题图
(2)如图①,作PF⊥PD于点P,使PF= OA,以PE,PF为邻边作矩形PEGF.当矩形PEGF的面积是△BOC面积的3倍时,求点P的坐标;
(2)令y=0,∴ ,
解得x1=-1,x2=4,
∴A点坐标为(4,0),
设直线AB的解析式是y=kx+m,
把A(4,0),B(0,3)代入
得 , 解得 ,
∴直线AB的解析式是 ,
设点P坐标为(x, ),则点E坐标为(x, ),
∴PE= ,
∴S矩形PEGF=PF·PE= OA·PE= ×4×PE=2(- x2+3x),
∵S△BOC= OC·OB= ×1×3= ,
∵S矩形PEGF=3S△BOC=3× = ,
∴ ,
解得x1=1,x2=3,
∴点P的坐标为(1, )或(3,3);
第3题图
(3)如图②,当点P运动到抛物线的顶点时,点Q在直线PD上,若以点Q,A,B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.
【解法提示】抛物线 对称轴为直线x= ,
如解图,过点B作BQ1⊥AB交对称轴于Q1,
过点A作AQ2⊥AB交对称轴于Q2,
∵A(4,0),B(0,3),
∴直线AB解析式为 ,
第3题图
Q1
∟
Q2
∟
∵BQ1⊥AB,
∴直线BQ1解析式为 ,
令 ,得 ,
∴Q1( ,5);
∵AQ2⊥AB,
∴直线AQ2解析式为 ,令x= ,得 ,
当∠AQB=90°时,AQ2+BQ2=AB2,设此时点Q的坐标为( ,n),
Q1
∟
Q2
∟
第3题图
∴ ,解得:n1= ,
t2= ,
∴当 ≤t≤ 时,∠AQC≥90°,
∵△ABQ为锐角三角形,
∴点Q( ,n)必须在线段Q1Q2上(不含端点Q1、Q2),
∴- <n< 或 <n<5.
(3)- <n< 或 <n<5.
第3题图
Q1
∟
Q2
∟
第3题图
【拓展设问】在(3)的条件下,若以点Q、A、B为顶点的三角形是钝角三角形,请直接写出点Q纵坐标n的取值范围.
由(3)知,∵△ABQ为钝角三角形,
∴点Q纵坐标n的取值范围为n< 或 <n< 或n>5.
微专题 二次函数与直角三角形问题
例1题图
微技能——分类讨论思想确定动点位置
一阶
例1 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C.连接AC.
一题多设问
探究1:在抛物线对称轴上找一点P使得△ACP为直角三
角形.
例1题图①
(1)若AC为斜边时,∠APC=90°;在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例1 探究1:(1)满足条件的点P如解图①
例1题解图①
【作图依据】__________________________
直径所对圆周角等于90°.
例1题图②
(2)若AC为直角边时,∠CAP=_____或∠ACP=_____;在图②中画出所有满足条件的点P的示意图(保留作图痕迹);
90°
90°
(2)满足条件的点P如解图②;
例1题解图②
例1题图③
探究2:在抛物线上找一点E使得△ACE为直角三角形.在图③中画出所有满足条件的点E的示意图(保留作图痕迹).
探究2: 满足条件的点E如解图③、④.
例1题解图③
例1题解图④
【方法总结】二次函数中直角三角形的存在性一般要分情况讨论:常以已知边为_____或________讨论;以自主探究1为例,已知边AC为斜边时,可以作以斜边AC为直径的圆,作图方法为:_______________,所找点即为___________的交点;若已知边AC为直角边时,作图方法为:_____________________________,所找点即为_____________的交点.
斜边
直角边
以AC为直径画圆
圆与对称轴
分别过点A,C作线段AC的垂线
垂线与对称轴
【思考】若动点在y轴上、x轴上时,确定动点位置有什么不同呢?
一题多设问
二阶
一题多设问
例2 如图,已知抛物线y= x2- x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,对称轴为直线l,顶点为M.
例2题图①
(1)求点A,B的坐标及抛物线的对称轴;
例2 解:(1)令y= x2- x-2=0,解得x1=-1,x2=4,
∵点A在点B的左侧,
∴点A的坐标为(-1,0),点B的坐标为(4,0).
∴抛物线的对称轴为直线x= ;
例2题图①
例2题图②
(2)若点G是x轴上一点,当△OCG为等腰直角三角形时,请直接写出点G的坐标;
【思维教练】由于点G在x轴上,可知∠COG=90°,要让它为等腰直角三角形,则需要分为当点G在x正半轴和负半轴两种情况讨论.
【解法提示】由题意知,点C的坐标为(0,-2).∴OC=2.
∵点G在x轴上,
∴当△OCG为等腰直角三角形时,
分点G在x轴正半轴和负半轴两种情况讨论:
①当点G在x轴正半轴时,
∵OC=OG,∴OG=2.
∴点G的坐标为(2,0);
②当点G在x轴负半轴时,
∵OC=OG,∴OG=2.
∴点G的坐标为(-2,0).
综上所述,满足条件的点G的坐标为(2,0)或(-2,0);
(2)点G的坐标为(2,0)或(-2,0);
例2题图②
例2题解图
(3)抛物线对称轴上是否存在点Q,使得△OCQ是以OC为直角边的直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由;
【思维教练】△OCQ是以OC为直角边的直角三角形,所以需分点O为直角顶点和点C为直角顶点两种情况讨论,进而求解.
【解法提示】如解图,∵点Q在抛物线的对称轴上,
∴设点Q的坐标为( ,q),
∵△COQ是以CO为直角边的直角三角形,
∴当∠COQ=90°时,点Q是对称轴与x轴的交点,
此时点Q的坐标为( ,0);当∠OCQ=90°时,CQ∥x轴,
∴点Q的坐标为( ,-2).
综上所述,满足条件的点Q的坐标为( ,0)或( ,-2);
(3)存在,点Q的坐标为( ,0)或( ,-2);
例2题解图
例2题图④
(4)若点N是对称轴上一点,是否存在点N使得△NBC是直角三角形,若存在,请直接写出点N的纵坐标;若不存在,请说明理由;
【思维教练】点N是对称轴l上一点,当△NBC是直角三角形时,需分∠NCB,∠NBC,∠BNC为直角时三种情况进行讨论,进而求解.
【解法提示】设点N的坐标为( ,t),
则CN2=( )2+(2+t)2,BN2=(4- )2+t2,BC2=20,
当△NBC是直角三角形时,分以下三种情况:
①当∠NCB=90°时,NC2+BC2=NB2,
即( )2+(2+t)2+20=(4- )2+t2,解得t=-5;
②当∠NBC=90°时,NB2+BC2=NC2,
即(4- )2+t2+20=( )2+(2+t)2,
解得t=5;
③当∠BNC=90°时,NB2+NC2=BC2,
即(4- )2+t2+( )2+(2+t)2=20,
解得t= 或 .
综上所述,当△NBC是直角三角形时,点N的纵坐标为-5或5或 或 ;
(4)存在.点N的纵坐标为-5或5或 或 ;
例2题图④
【拓展设问】点N是对称轴上一点,若△NBC是锐角三角形时,请直接写出点N的纵坐标n的取值范围.
【思考】若△NBC是钝角三角形时,点N的纵坐标n的取值范围是什么.
【拓展设问】由(4)知,当∠NCB=90°时,t=-5,当∠NBC=90°时,t=5,当∠BNC=90°时,t= 或t= ,
结合图象可知,当△NBC是锐角三角形时,点N的纵坐标n的取值范围是-5<n< 或 <n<5;
【思考】同理可得当△NBC是钝角三角形时,点N的纵坐标n的取值范围是n<-5或 <n< 或n>5.
例2题图⑤
(5)点D是y轴上一点,其坐标为(0,4).动点E是直线BD上一点,过点E作EF⊥BD,交y轴于点F,连接AF,BF,若△ABF是直角三角形,试求点E的坐标.
【思维教练】点F在y轴上,所以当△ABF是直角三角形时,∠FAB和∠FBA不可能是直角,所以只能是∠AFB为直角,
当∠AFB为直角时,注意要分点F在y轴的正、负半轴
两种情况讨论.
(5)∵点D在y轴上,且点D的坐标为(0,4),点B的坐标为(4,0),
∴直线BD的函数表达式为y=-x+4,
∵点E是直线y=-x+4上一点,
∴设点E的坐标为(m,-m+4),
∵EF⊥BD,
∴易得直线EF的函数表达式为y=x-2m+4.
∴点F的坐标为(0,-2m+4).
∴AF2=12+(-2m+4)2,BF2=42+(-2m+4)2,AB2=52=25.
例2题图⑤
∵点F在y轴上,
∴只能有∠AFB=90°.即AF2+BF2=AB2.
即12+(-2m+4)2+42+(-2m+4)2=25.
解得m=1或3.
当m=1时,点E的坐标为(1,3);
当m=3时,点E的坐标为(3,1).
综上所述,当△ABF是直角三角形时,点E的坐标为(1,3)或(3,1).
例2题图⑤
综合训练
三阶
第1题图
1.如图,在平面直角坐标系中,抛物线y=-x2+bx+c的图象与坐标轴相交于A、B、C三点,其中A点坐标为(3,0),B点坐标为(-1,0),连接AC、BC.动点P从点A出发,在线段AC上以每 秒个单位长度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
(1)求b、c的值.
解:(1)∵抛物线y=-x2+bx+c经过点A(3,0),B(-1,0),
则 ,解得
第1题图
第1题图
(2)在P、Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?
(2)由(1)得,抛物线表达式为y=-x2+2x+3,C(0,3),A(3,0),
∴△OAC是等腰直角三角形,由点P的运动可知AP= t,
如解图,过点P作PE⊥x轴,垂足为E,
∴AE=PE= =t,即E(3-t,0),
E
∟
= ×4×3- ×[3-(-1+t)]t= t2-2t+6,
∵当其中一点到达终点时,另一点随之停止运动,
AC= ,AB=4,
∴0≤t≤3,
∵ >0,∴当t=2时,四边形BCPQ的面积最小,
最小值为 ×22-2×2+6=4;
E
∟
又Q(-1+t,0),
∴S四边形BCPQ=S△ABC-S△APQ
第1题图
(3)在线段AC上方的抛物线上是否存在点M,使△MPQ是以点P为直角顶点的等腰直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
(3)存在点M,使△MPQ是以点P为直角顶点的等腰直角三角形.
理由如下:
∵点M是线段AC上方的抛物线上的点,
第1题解图②
如解图②,过点P作x轴的垂线,交x轴于点E,
过M作EP的垂线交EP的延长线于点F,
∵△PMQ是等腰直角三角形,PM=PQ,∠MPQ=90°,
∴∠MPF+∠QPE=90°,又∠MPF+∠PMF=90°,
∴∠PMF=∠QPE,
在△PFM和△QEP中,
∴△PFM≌△QEP(AAS),
第1题解图②
∴MF=PE=t,PF=QE=4-2t,
∴EF=4-2t+t=4-t,
∴点M的坐标为(3-2t,4-t),
∵点M在抛物线y=-x2+2x+3上,
∴4-t=-(3-2t)2+2(3-2t)+3,
解得t= 或 (舍去),
∴点M的坐标为( , ).
第1题解图②
第2题图
2.已知抛物线y=ax2+bx+c与x轴交于A(-2,0)、B(6,0)两点,与y轴交于点C(0,-3).
(1)求抛物线的表达式;
解:(1)设抛物线的表达式为y=a(x+2)(x-6),
把点C(0,-3)代入,得-3=a(0+2)(0-6),
解得a= ,
∴抛物线的表达式为:
y= (x+2)(x-6)= x2-x-3;
第2题图
(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当 最大时,求点P的坐标及 的最大值;
设点P的坐标为(n, n2-n-3)(0<n<6),则OE=n,
设直线AP的解析式为y=kx+b(k≠0),
根据题意得 解得
(2)如解图,过点P作PE⊥x轴于点E,过点M作MF⊥x轴于点F,
则MF∥PE,
F
∟
E
∟
∴直线AP的解析式为y= (n-6)x+ (n-6),
设直线BC的解析式为y=mx+a(m≠0),
根据题意得 解得
,
∴直线BC的解析式为y= x-3,
联立直线AP和BC的解析式
得 解得
第2题图
F
∟
E
∟
即点M的坐标为( , ),则OF= ,
∴EF= = ,AF= ,
又∵MF∥PE,
∴
,
∴
第2题图
F
∟
E
∟
∵ <0,0<n<6,
∴当n=3时, 有最大值,最大值为 ,
此时点P的坐标为(3, ), 的最大值为 .
第2题图
F
∟
E
∟
第2题图
(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使△BCD是直角三角形,若存在,请直接写出点D的坐标;若不存在,请说明理由.
【解法提示】设点D的坐标为(3,m),∵B(6,0),C(0,-3),
∴BD2=m2+9,CD2=(m+3)2+9,BC2=45,
①当∠BCD=90°时,有BD2=CD2+BC2,
∴m2+9=(m+3)2+9+45,
整理得:6m=-54,解得m=-9,
∴点D的坐标为(3,-9);
②当∠BDC=90°时,有BC2=BD2+CD2,
∴45=m2+9+(m+3)2+9,整理得.m2+3m-9=0
解得m1= ,m2= ,
∴点D的坐标为(3, )或(3, );
③当∠CBD=90°时,有CD2=BC2+BD2,
∴(m+3)2+9=45+m2+9,
解得m=6,
∴点D的坐标为(3,6);
第2题图
综上所述,满足条件的点D坐标为(3,-9)或(3,6)或(3, )或(3, ).
(3)存在点D,使△BCD是直角三角形,点D的坐标为(3,-9)或(3,6)或(3, )或(3, ).
第2题图
备用图
3.如图,抛物线y=- x2+bx+c与x轴交于点A和点C(-1,0),与y轴交于点B(0,3),连接AB,BC,点P是抛物线第一象限上的一动点,过点P作PD⊥x轴于点D,交AB于点E.
第3题图
(1)求抛物线的解析式;
解:(1)∵抛物线y=- x2+bx+c经过C(-1,0),B(0,3)两点,
∴ ,解得
∴抛物线的解析式为:
;
第3题图
(2)如图①,作PF⊥PD于点P,使PF= OA,以PE,PF为邻边作矩形PEGF.当矩形PEGF的面积是△BOC面积的3倍时,求点P的坐标;
(2)令y=0,∴ ,
解得x1=-1,x2=4,
∴A点坐标为(4,0),
设直线AB的解析式是y=kx+m,
把A(4,0),B(0,3)代入
得 , 解得 ,
∴直线AB的解析式是 ,
设点P坐标为(x, ),则点E坐标为(x, ),
∴PE= ,
∴S矩形PEGF=PF·PE= OA·PE= ×4×PE=2(- x2+3x),
∵S△BOC= OC·OB= ×1×3= ,
∵S矩形PEGF=3S△BOC=3× = ,
∴ ,
解得x1=1,x2=3,
∴点P的坐标为(1, )或(3,3);
第3题图
(3)如图②,当点P运动到抛物线的顶点时,点Q在直线PD上,若以点Q,A,B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.
【解法提示】抛物线 对称轴为直线x= ,
如解图,过点B作BQ1⊥AB交对称轴于Q1,
过点A作AQ2⊥AB交对称轴于Q2,
∵A(4,0),B(0,3),
∴直线AB解析式为 ,
第3题图
Q1
∟
Q2
∟
∵BQ1⊥AB,
∴直线BQ1解析式为 ,
令 ,得 ,
∴Q1( ,5);
∵AQ2⊥AB,
∴直线AQ2解析式为 ,令x= ,得 ,
当∠AQB=90°时,AQ2+BQ2=AB2,设此时点Q的坐标为( ,n),
Q1
∟
Q2
∟
第3题图
∴ ,解得:n1= ,
t2= ,
∴当 ≤t≤ 时,∠AQC≥90°,
∵△ABQ为锐角三角形,
∴点Q( ,n)必须在线段Q1Q2上(不含端点Q1、Q2),
∴- <n< 或 <n<5.
(3)- <n< 或 <n<5.
第3题图
Q1
∟
Q2
∟
第3题图
【拓展设问】在(3)的条件下,若以点Q、A、B为顶点的三角形是钝角三角形,请直接写出点Q纵坐标n的取值范围.
由(3)知,∵△ABQ为钝角三角形,
∴点Q纵坐标n的取值范围为n< 或 <n< 或n>5.
同课章节目录
