圆的切线的判定课件
图片预览




文档简介
课件16张PPT。圆的切线的判定邵阳市第十五中学
彭雯
2018年11月28日8时46分温故知新1.直线和圆有哪些位置关系?圆心到直线l的距离d和圆的半径r之间有什么数量关系?
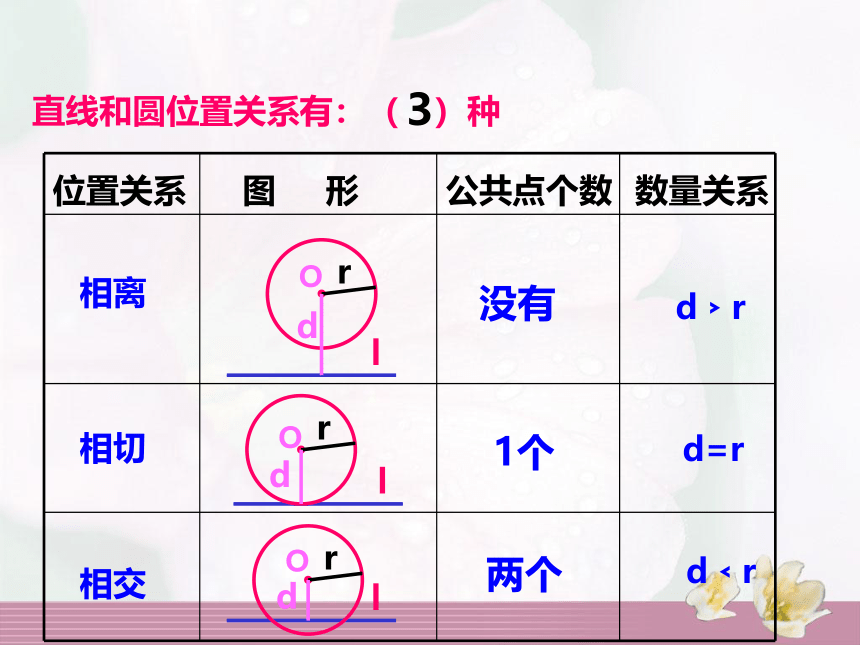
直线和圆位置关系有:( )种3图 形位置关系公共点个数数量关系相离相切相交1个没有两个d﹥rd=rd﹤r温故知新
2.什么叫直线与圆相切?如何判定?
答:直线和圆只有一个公共点叫直线和圆相切
可以(1)根据直线和圆只有一个公共点判定
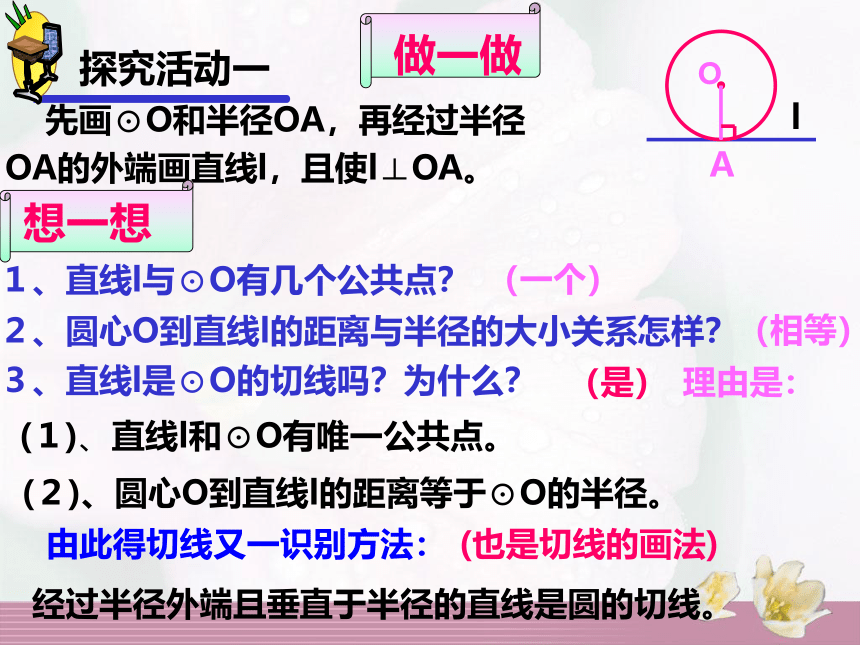
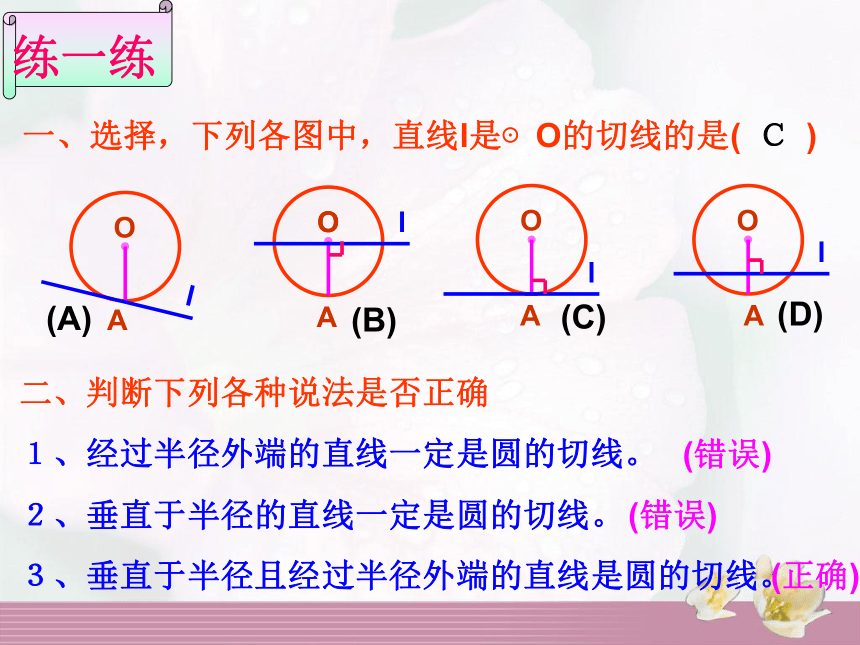
(2)根据圆心到直线的距离d等于圆的半径r来判定 先画⊙O和半径OA,再经过半径OA的外端画直线l,且使l⊥OA。1、直线l与⊙O有几个公共点?2、圆心O到直线l的距离与半径的大小关系怎样?3、直线l是⊙O的切线吗?为什么?(一个)(相等)A(是)(1)、直线l和⊙O有唯一公共点。(2)、圆心O到直线l的距离等于⊙O的半径。理由是:由此得切线又一识别方法:经过半径外端且垂直于半径的直线是圆的切线。(也是切线的画法)探究活动一一、切线的判定方法:1、定义:直线和圆有唯一公共点。2、圆心到直线的距离等于圆的半径。3、经过半径外端且垂直于的直线是圆的切线。 推理形式: ∵ OA 是⊙O的半径,∴直线l是⊙O的切线。且l⊥OA于点A。(经过半径外端且垂直于半径的直线是圆的切线)探究活动一一、选择,下列各图中,直线l是⊙O的切线的是( )C二、判断下列各种说法是否正确2、垂直于半径的直线一定是圆的切线。1、经过半径外端的直线一定是圆的切线。3、垂直于半径且经过半径外端的直线是圆的切线。(错误)(错误)(正确)探究活动一 利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。结论〖例1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可。 证明:连结OC(如图)。
∵ OA=OB,CA=CB,
∴ AB⊥OC(三线合一)
∵ OC是⊙O的半径
∴ AB是⊙O的切线。探究活动二〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
OD⊥AB于点D
∴ OE=OD
∵ OD是⊙O的半径
∴ OE也是半径
∴ AC是⊙O的切线。探究活动二小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:有交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无交点,作垂直,证半径。探究活动二分析: AB =AC∠C=45AC⊥AB直线AC经过⊙O的点A直线AC是圆⊙O的切线。∠B=45∠B=45(已知)(已知)(已知)(已知)如图AB是⊙O的直径,∠B=45 °,AC=AB。AC是⊙O的切线吗?为什么?°°°如图AB是⊙O的直径,∠B=45°,AC=AB。AC是的切线吗?为什么?理由:在△ABC中, AB =AC ∠B=45°∴∠C=∠B=45°(等边对等角)∴∠ CAB=180°- ∠C- ∠B=(三角形的内角和等于180° )90°∴ AC⊥AB又∵直线AC经过⊙O的点A∴直线AC是圆⊙O的切线。(垂直的定义)(经过半径外端且垂直于半径的直线是圆的切线)解:直线AC是圆⊙O的切线。1. 判定切线的方法有哪些?直线l 与圆有唯一公共点与圆心的距离等于圆的半径经过半径外端且垂直这条半径l是圆的切线2. 常用的添辅助线方法? ⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)l是圆的切线l是圆的切线课堂小结1、如图,AB是⊙O的直径,直线FE过点A,如果要使FE是⊙O的切线,还需添加的条件是:①、( )②、( )③、( )∠1+∠2=90°AB⊥FE∠FAB=90°∠EAB=90°④、( )⑤、( )∠2=∠B12拓展提升布置作业
1、必做P75A组2,3
2、选做P76B组9
彭雯
2018年11月28日8时46分温故知新1.直线和圆有哪些位置关系?圆心到直线l的距离d和圆的半径r之间有什么数量关系?
直线和圆位置关系有:( )种3图 形位置关系公共点个数数量关系相离相切相交1个没有两个d﹥rd=rd﹤r温故知新
2.什么叫直线与圆相切?如何判定?
答:直线和圆只有一个公共点叫直线和圆相切
可以(1)根据直线和圆只有一个公共点判定
(2)根据圆心到直线的距离d等于圆的半径r来判定 先画⊙O和半径OA,再经过半径OA的外端画直线l,且使l⊥OA。1、直线l与⊙O有几个公共点?2、圆心O到直线l的距离与半径的大小关系怎样?3、直线l是⊙O的切线吗?为什么?(一个)(相等)A(是)(1)、直线l和⊙O有唯一公共点。(2)、圆心O到直线l的距离等于⊙O的半径。理由是:由此得切线又一识别方法:经过半径外端且垂直于半径的直线是圆的切线。(也是切线的画法)探究活动一一、切线的判定方法:1、定义:直线和圆有唯一公共点。2、圆心到直线的距离等于圆的半径。3、经过半径外端且垂直于的直线是圆的切线。 推理形式: ∵ OA 是⊙O的半径,∴直线l是⊙O的切线。且l⊥OA于点A。(经过半径外端且垂直于半径的直线是圆的切线)探究活动一一、选择,下列各图中,直线l是⊙O的切线的是( )C二、判断下列各种说法是否正确2、垂直于半径的直线一定是圆的切线。1、经过半径外端的直线一定是圆的切线。3、垂直于半径且经过半径外端的直线是圆的切线。(错误)(错误)(正确)探究活动一 利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。结论〖例1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可。 证明:连结OC(如图)。
∵ OA=OB,CA=CB,
∴ AB⊥OC(三线合一)
∵ OC是⊙O的半径
∴ AB是⊙O的切线。探究活动二〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
OD⊥AB于点D
∴ OE=OD
∵ OD是⊙O的半径
∴ OE也是半径
∴ AC是⊙O的切线。探究活动二小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:有交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无交点,作垂直,证半径。探究活动二分析: AB =AC∠C=45AC⊥AB直线AC经过⊙O的点A直线AC是圆⊙O的切线。∠B=45∠B=45(已知)(已知)(已知)(已知)如图AB是⊙O的直径,∠B=45 °,AC=AB。AC是⊙O的切线吗?为什么?°°°如图AB是⊙O的直径,∠B=45°,AC=AB。AC是的切线吗?为什么?理由:在△ABC中, AB =AC ∠B=45°∴∠C=∠B=45°(等边对等角)∴∠ CAB=180°- ∠C- ∠B=(三角形的内角和等于180° )90°∴ AC⊥AB又∵直线AC经过⊙O的点A∴直线AC是圆⊙O的切线。(垂直的定义)(经过半径外端且垂直于半径的直线是圆的切线)解:直线AC是圆⊙O的切线。1. 判定切线的方法有哪些?直线l 与圆有唯一公共点与圆心的距离等于圆的半径经过半径外端且垂直这条半径l是圆的切线2. 常用的添辅助线方法? ⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)l是圆的切线l是圆的切线课堂小结1、如图,AB是⊙O的直径,直线FE过点A,如果要使FE是⊙O的切线,还需添加的条件是:①、( )②、( )③、( )∠1+∠2=90°AB⊥FE∠FAB=90°∠EAB=90°④、( )⑤、( )∠2=∠B12拓展提升布置作业
1、必做P75A组2,3
2、选做P76B组9
