三角形内角和课件

课件26张PPT。三角形内角和邵阳市第十五中学
彭雯
2018年11月28日8时46分 三角形蓝和三角形红见面了，蓝炫耀的说：“我的面积比你大，所以我的内角和也比你大！”红不服气的说：“那可不好说噢，你自己量量看！”
同学们，你们觉得谁说的对？情景引入探究活动一要求：1.利用手中的三角形纸片 及你手中的工具，求出三角形内角和的度数
2.分学习小组进行
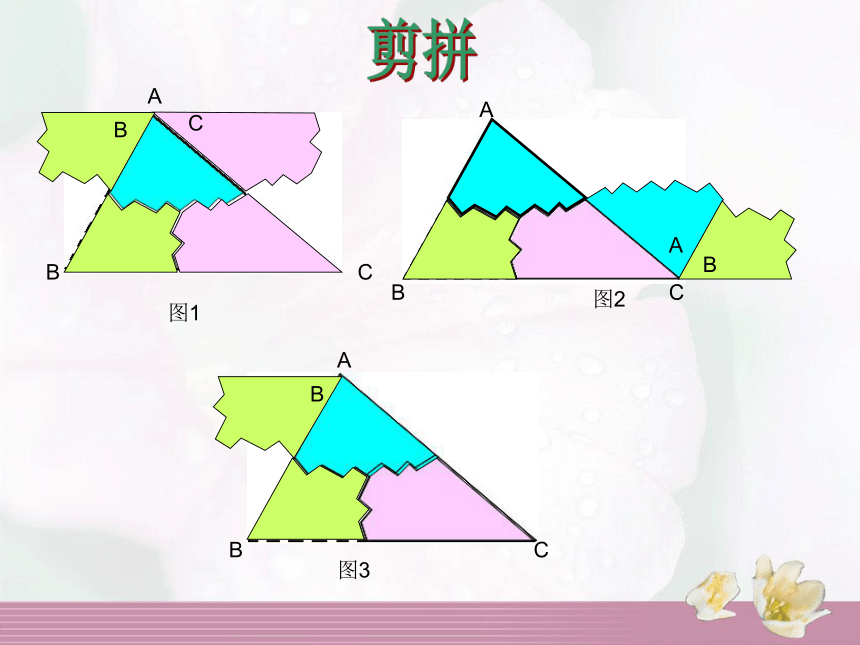
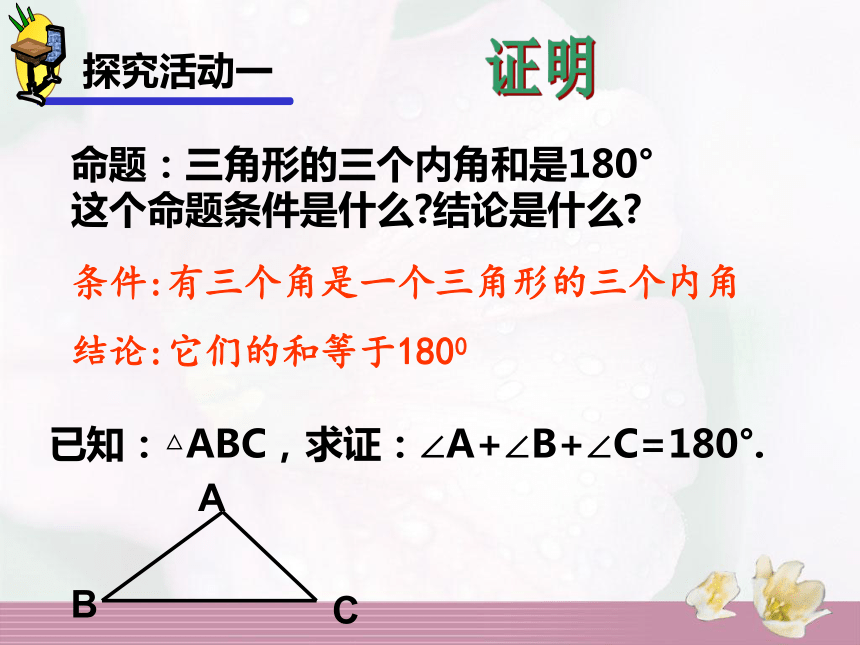
时间：3分钟探究活动一拿出你手中的三角板，算一算三角形内角和是多少度呢？度量图1图2 图3ABCAABBCC剪拼演示下一页折叠探究活动一命题：三角形的三个内角和是180°
这个命题条件是什么?结论是什么?证明条件:有三个角是一个三角形的三个内角
结论:它们的和等于1800已知：△ABC，求证：∠A+∠B+∠C=180°.１．平角的度数是180°２．两直线平行，同旁内角的和是180°3 . 邻补角的和是180 °问题：有什么方法可以得到180°探究活动一启发（1）拼图的过程是在做什么？（2）移角的目的是什么？（3）何处能提供180°？
（4）怎样构造平角或同旁内角？　（移角）（构造角的和是180°）（平角或同旁内角） （作平行线）探究活动一 图3ABC
证明：过点A作EF∥BC则∠B=∠2（两直线平行,内错角相等）
同理∠C=∠1因为∠2+∠1+∠BAC=1800（平角定义） 所以∠B+∠C+∠BAC=1800（等量代换）已知：△ABC.求证：∠A +∠B +∠C =180°E F探究活动一已知：△ABC. 求证：∠A +∠B +∠C =180°21EDCBA 在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线。在平面几何里，辅助线通常画成虚线。思路总结 为了证明三个角的和为1800,把这三个角转化为一个平角或构成一组同旁内角,这种转化思想是数学中的常用方法.探究活动一结论三角形的内角和是180°符号语言：在△ABC中,
∠A+∠B+∠C=180°探究活动二一个三角形中能有两个直角吗？
一个三角形中能有两个钝角吗？
三个内角都能小于60°吗？不能不能不能探究活动二三个角都是锐角的三角形叫锐角三角形
有一个角是直角的三角形叫直角三角形
有一个角是钝角的三角形叫钝角三角形三角形按角分类 在△ABC中，∠A的度数是∠B的度数的3倍，
∠C 比∠B 大15°，求∠A，∠B，∠C的度数.解 设∠B为x °，则∠A为(3x)°，∠C为(x+ 15)°，从而有 3x+x+(x+15)=180.解得 x=33.所以 3x=99 ，x+15 =48.答：∠A，∠B，∠C的度数分别
为99°，33°，48°.探究活动二典型例题123456在△ABC中,∠A=35°,∠ B=43°，
则∠ C= .102°填一填x=______ y=__________30°算一算59°恭喜你，加20分！∠α=_______算一算28°恭喜你，加20分！ 下面哪三个角能组成一个三角形？为什么？ 60°40°80°（2）115°35°40°　30°（1）70°圈一圈课堂小结1、知识点：三角形内角和为180°
2、方法：
（1）通过思考、去探究三角形内角和定理，并且发现要证明三角形三个内角的和等于180 °需通过作辅助线转化为：①平角;②两直线平行同旁内角和等于180°;③邻补角。
（2）利用方程或方程组求角
（3）把分散的角集中到三角形或多边形上。如图，则∠1＋∠2＋∠3＋∠4＝____解：连结BD，则
∠1＋∠2＋∠3＋∠4＝180°＋180°＝360°ABC能力提高，拾级而上 拓展提升布置作业
1、必做P49A组4
2、选做P49B组8