2024辽宁中考数学二轮专题复习 微专题 二次函数与矩形、菱形、正方形问题 课件(共43张PPT)
文档属性
| 名称 | 2024辽宁中考数学二轮专题复习 微专题 二次函数与矩形、菱形、正方形问题 课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 858.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 20:37:19 | ||
图片预览









文档简介
(共43张PPT)
微专题 二次函数与矩形、菱形、正方形问题
微技能——分类讨论思想确定对应关系
一阶
一题多设问
设问突破
二阶
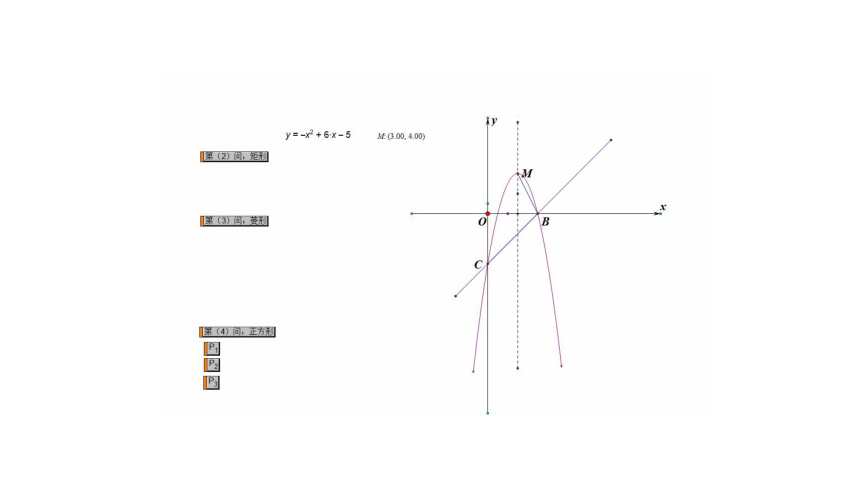
例1 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(5,0)两点,与y轴交于点C.点P是抛物线上一个动点,过点P作x轴的垂线,垂足为点H,交直线BC于点E.
例1题图①
(1)求抛物线的解析式;
例1题图①
(1)将A(1,0),B(5,0)代入y=-x2+bx+c中,
得
解得
∴抛物线解析式为y=-x2+6x-5 ;
(2)如图②,设点M是抛物线对称轴上一点,点N是平面内一点,是否存在点M,使得以B,C,M,N为顶点的四边形是矩形?若存在,求出点M的坐标;若不存在,请说明理由;
【思维教练】要求使得以B,C,M,N为顶点的四边形是矩形的点M的坐标,已知点M是抛物线对称轴上一点,设点M的坐标,分别求出BC,BM,CM的长,然后根据矩形的性质分别讨论∠CBM,∠BCM,∠CMB为直角的情况,利用勾股定理列方程求解.
例1题图②
M
N
(2)存在.
易得抛物线对称轴为直线x=3,
∵点M是对称轴上一点,设点M的坐标为(3,m),
易得BC2=52+52=50,BM2=(5-3)2+m2=4+m2,
①如解图①,连接CM,CM2=32+(m+5)2=m2+10m+34,
例1题解图①
若∠CBM=90°,
则BC2+BM2=CM2,
即50+4+m2=m2+10m+34, 解得m=2,
此时点M的坐标为(3,2);
M
N
②如解图②, 若∠BCM=90°.
则BC2+CM2=BM2,
即50+m2+10m+34=4+m2,
解得m=-8,
此时点M的坐标为(3,-8);
M
N
例1题解图②
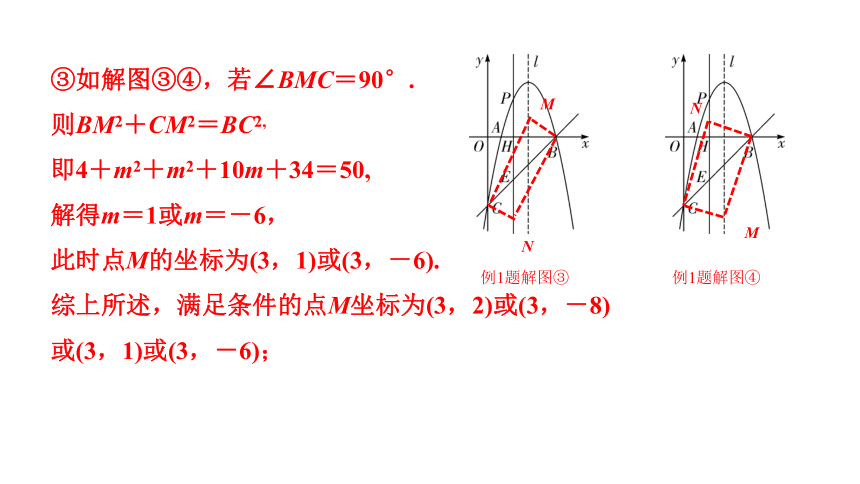
③如解图③④,若∠BMC=90°.
则BM2+CM2=BC2,
即4+m2+m2+10m+34=50,
解得m=1或m=-6,
此时点M的坐标为(3,1)或(3,-6).
综上所述,满足条件的点M坐标为(3,2)或(3,-8)或(3,1)或(3,-6);
M
M
N
N
例1题解图③
例1题解图④
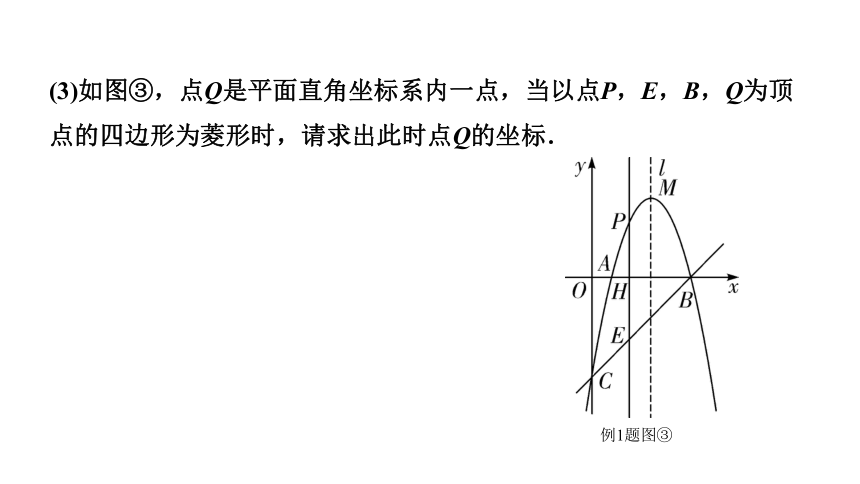
(3)如图③,点Q是平面直角坐标系内一点,当以点P,E,B,Q为顶点的四边形为菱形时,请求出此时点Q的坐标.
例1题图③
例1题图③
【思维教练】设点P的坐标为(x,-x2+6x-5),则点E的坐标为(x,x-5),共分为四种情况讨论:①当PH=HE,QH=HB时,四边形PQEB是菱形;②当点P在x轴上方,且PE=EB=BQ=QP时,四边形PEBQ为菱形;③当点P与点A重合,且PB=PE=EQ=QB时,四边形PEQB是菱形;④当点P在x轴下方,且PE=EB=BQ=QP时,四边形PEBQ为菱形.
例1题图③
(3)设点P的坐标为(x,-x2+6x-5)
设直线BC的解析式为y=kx+b(k≠0);
将B(5,0),C(0,5)代入得
解得
∴直线BC的解析式为y=x-5,则点E的坐标为(x,x-5),
例1题解图⑤
如解图⑤
∵PE⊥QB,
∴当PH=HE,QH=HB时,四边形PQEB是菱形.
此时yP=-yE,即-x2+6x-5=-(x-5),
解得x1=2,x2=5(不合题意,舍去),
∴QH=HB=3,
∴点Q的坐标为(-1,0);
例1题解图⑥
如解图⑥,当点P在x轴上方,
且PE=EB=BQ=QP时,四边形PEBQ为菱形.
∵PE=-x2+6x-5-(x-5)=-x2+5x,BE= BH= (5-x),
∴-x2+5x= (5-x),
解得x1=5(不合题意,舍去),x2= .
当x= 时,BQ=PE= ,
∴点Q的坐标为(5, );
例1题解图⑦
如解图⑦,当点P与点A重合时,PB=PE.
∴当PB=PE=EQ=QB时,四边形PEQB是菱形.
易得Q的坐标为(5,-4);
例1题解图⑧
如解图⑧,当点P在x轴下方,
且PE=EB=BQ=QP时,四边形PEBQ为菱形.
∵PE=x-5-(-x2+6x-5)=x2-5x,
BE= BH= (5-x),
∴x2-5x= (5-x),
解得x1=5(不合题意,舍去),x2=- .
当x=- 时,QB=PE= ,
∴点Q的坐标为(5, ).
综上所述,存在点Q,使得以点P,E,B,Q为顶点的四边形为菱形.此时点Q的坐标为(-1,0),(5, ),(5,-4)或(5, ).
(4)如图④,点M是抛物线的顶点,坐标平面内是否存在点P、Q(点P在点Q左侧),使得以B,M,P,Q为顶点的四边形是正方形?若存在,直接写出点P的坐标;若不存在,说明理由.
【思维教练】由BM为定边,可分以BM为正方形的边或以BM为正方形的对角线来确定点P.
例1题图④
【解法提示】当MB为正方形的边时,
①当点P在点M的左侧时,如解图⑨,
∵点M为抛物线的顶点,
∴M点坐标为(3,4),
∵B(5,0),
∴BM= ,
∴BM=PM= ,
设P1(m,n),过点P1作P1N1⊥x轴于点N1,
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
∴BN1=5-m,P1N1=n,
∴P1O= ,
P1B= ,
P1M= ,
解得m=-1,n=2,
∴P1(-1,2);
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
②当点P在点M右侧时,如解图⑨,
∵点P2与点P1关于直线BM对称,
∴P2(3×2+1,4×2-2),即P2(7,6);
当MB为正方形的对角线时,
∵点P在点Q左侧,
∴点P只能在点M的左侧,如解图⑨,
∵BM= ,
∴P3B=PM= ,
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
设P3(m,n),
∴P3B= ,
P3M= ,
解得m=2n,
∵点P3与点Q3关于直线MB对称,
∴Q3(5+n,5-m), ,
∴3n=3,n=1,∴m=2n=2,∴P3(2,1),
综上所述,存在点P,使得以B,M,P,Q为顶点的四边形为正方形,此时点P的坐标为(-1,2),(7,6),(2,1).
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
综合训练
三阶
第1题图
1. (2023抚本铁辽葫定心卷)如图,抛物线y=ax2+x+c(a≠0)交 x轴于点A(4,0)、B,交 y轴于点C(0,4).
(1)求抛物线的解析式;
(1)∵抛物线y=ax2+x+c(a≠0)
经过A(4,0),C(0,4)两点,
∴c= 解得
∴抛物线的解析式为y=- x2+x+4;
(2)∵点E是OA的中点,∴E(2,0).
由题意易知直线CE的解析式为y=-2x+4.
∵直线MN到y轴的距离为 ,
∴点D的坐标为( ,0)或(- ,0).
当D( ,0)时,点M、N的横坐标为 ,
将x= 代入y=-2x+4中,得y=1,
(2)如图①,点E是OA的中点,点D是线段BE上一点(不与点B、E重合),过点D作x轴的垂线,交直线CE于点M,交抛物线于点N,若直线MN到y轴的距离为 ,求点M与点N之间的距离;
第1题图
将x= 代入y=- x2+x+4中,得y= .
∴M( ,1),N( ),
∴MN= ;
当D(- ,0)时,点M、N的横坐标为- ,
将x=- 代入y=-2x+4中,得y=7,
将x=- 代入y=- x2+x+4中,得y= .
第1题图
∴M(- ,7),N(- , ),
∴MN=7- = .
∴点M与点N之间的距离为 或 ;
第1题图
第1题图
(3)如图②,点F在抛物线的对称轴上且在x轴上方,点G在坐标平面内,当以点B、C、F、G为顶点的四边形为菱形时,请直接写出点F的坐标.
【解法提示】已知抛物线解析式为y=- x2+x+4,
令y=0,即- x2+x+4=0,解得x1=-2,x2=4,
∴B(-2,0),抛物线的对称轴为直线x=1.
设点F的坐标为(1,m).
∵C(0,4),
∴BC2=OB2+OC2=20,BF2=9+m2 ,CF2=1+(m-4)2 .
要使以点B、C、F、G为顶点的四边形为菱形,分两种情况讨论,
当BC为菱形的边时,
①当BC=BF时,即20=9+m2 ,
解得m1= ,m2=- (不符合题意,舍去),
∴点F的坐标为(1, );
②当BC=CF时,
即20=1+(m-4)2,
解得m3=4+ ,m4=4- (不符合题意,舍去),
∴点F的坐标为(1,4+ );
第1题图
当BC为菱形的对角线时,则点F在线段BC的垂直平分线上.
∴BF=CF,
即9+m2=1+(m-4)2,
解得m=1.
∴点F的坐标为(1,1),
综上所述,点F的坐标为(1, )或(1,4+ )
或(1,1).
(3)点F的坐标为(1, )或(1,4+ )或(1,1).
第1题图
2. 如图,已知抛物线y=ax2-2ax+b与x轴交于点A(-2,0)和点B,与y轴交于点C(0,4).
(1)求抛物线的解析式;
第2题图
备用图
解:(1)将点A、C的坐标分别代入抛物线的解析式,
得 解得
∴抛物线的解析式为y= x2+x+4;
(2)点P是第四象限抛物线上一点,连接AC、AP,当∠PAB=2∠ACO时,求点P的坐标;
(2)如解图,在OB上取一点R,使OR=OA=2,连接CR,
则∠ACR=2∠ACO=∠PAB,
过点A作AK⊥CR于点K,设直线AP交y轴于点H,
H
R
第2题图
在y=- x2+x+4中,令y=0,
即- x2+x+4=0,
解得x1=-2(舍去),x2=4,
∴B(4,0).
K
∵A(-2,0),C(0,4),
∴AR=4,OC=4,AC=CR=
∴S△ACR= AR·OC= CR·AK,
即 ×4×4= 解得AK= ,
∴CK= ,
∴tan∠ACK=
H
R
第2题图
K
∵∠PAB=2∠ACO=∠ACK,
∴tan∠ACK=tan∠PAB.
在Rt△AOH中,OH=OA·tan∠PAB= .
∴H(0, ).
由点A、H的坐标得直线AP的解析式为y= .
联立 解得 或 (舍去),
∴点P的坐标为( );
H
R
第2题图
K
(3)点M是抛物线的对称轴上一动点,在平面内是否存在点N,使得以M、N、B、C为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
第2题图
【解法提示】∵y= x2+x+4,
∴抛物线的对称轴为直线x=1.
设点M的坐标为(1,m),
∵B(4,0),C(0,4),
∴BM2=9+m2,CM2=m2-8m+17,BC2=32.
当以M、N、B、C为顶点的四边形是矩形时,需分以BC为边和BC为对角线两种情况讨论.
①当BC为边时,以M、B、C为顶点的三角形是以BC为直角边的直角三角形,则分以MC为斜边和以MB为斜边,
当以MC为斜边时,BC2+BM2=CM2,即32+9+m2=m2-8m+17,解得m=-3,
∴点M的坐标为(1,-3).
由xC+xM=xB+xN,得xN=-3,同理可得yN=1,
∴点N的坐标为(-3,1);
第2题图
当以MB为斜边时,
BC2+CM2=BM2,即32+m2-8m+17=m2+9,
解得m=5,∴M(1,5).
由xB+xM=xC+xN,得xN=5,
同理可得yN=1,∴点N的坐标为(5,1);
②当以BC为对角线时,以M、B、C为顶点的三角形是以BC为斜边的直角三角形,则BM2+CM2=BC2,即9+m2+m2-8m+17=32,
解得m1=2+ ,m2=2- ,
∴点M的坐标为(1,2+ )或(1,2- ),
第2题图
由xB+xC=xM+xN,得xN=3,
同理可得yN=2- 或2+ ,
∴点N的坐标为(3,2- )或(3,2+ ).
综上所述,存在点N
使得以M、N、B、C为顶点的四边形是矩形,满足条件的点N的坐标为(-3,1)或(5,1)或(3,2- )或(3,2+ ).
(3)存在,点N的坐标为(-3,1)或(5,1)或(3,2- )或(3,2+ ).
第2题图
3. 直线y=-x+3与x轴相交于点A,与y轴相交于点B,抛物线y=ax2+2x+c经过点A,B,与x轴的另一个交点为C.
(1)求抛物线的解析式;
第3题图①
备用图
(1)在y=-x+3中,令y=0,则x=3,
令x=0,则y=3,
∴A(3,0),B(0,3),
把A(3,0),B(0,3)代入y=ax2+2x+c得, ∴
∴抛物线的解析式为y=-x2+2x+3;
(2)如图①,点D是第一象限内抛物线上的一个动点,过点D作DE∥y轴交AB于点E,DF⊥AB于点F,FG⊥x轴于点G,当DE=FG时,求点D的坐标;
第3题图①
由(1)可知抛物线的解析式为y=-x2+2x+3,
直线AB的解析式为y=-x+3,
设D(m,-m2+2m+3),
∵DE∥y轴,∴E(m,-m+3),
∴DE=-m2+2m+3-(-m+3)=-m2+3m,ME=-m+3,
(2)如解图,延长DE交x轴于点M,则DM⊥x轴
M
∵B(0,3),A(3,0)∴OB=OA=3,∴∠OBA=∠OAB=45°,
∵DM⊥x轴,DF⊥AB,∴∠DEF=∠AEM=45°,
∴DE= EF,AF= FG,
∵DE=FG,∴AF=2EF,∴AE=EF,
∵FG⊥x轴,∴FG∥ME,
∴ ∴FG=2ME,
∴DE=2ME,∴-m2+3m=2(-m+3),
∴m=2或m=3(舍去),
∴D(2,3);
第3题图①
M
(3)如图②,在(2)的条件下,直线CD与AB相交于点M,点H在抛物线上,过点H作HK∥y轴,交直线CD于点K.P是平面内一点,当以点M,H,K,P为顶点的四边形是正方形时,请直接写出点P的坐标.
第3题图②
【解法提示】在y=-x2+2x+3中,令y=0,则-x2+2x+3=0,
解得x=-1或x=3,∴点C的坐标为(-1,0),
设直线CD的解析式为y=kx+b,根据题意得
解得 ,
∴直线CD的解析式为y=x+1.
联立直线CD与直线AB的解析式得 解得
∴点M的坐标为(1,2).
①当MK为正方形边时,则MH⊥MK时,
H点在AB上,K点在CD上.
∵H点在抛物线上,∴H(3,0)或H(0,3);
当H(3,0)时,MH= ,∴KH=4,
∴K(3,4)
∴HK的中点为(3,2),则MP的中点为(3,2);
∴P(5,2);
第3题图②
当H(0,3)时,MH= ,∴KH=2,∴K(0,1),
∴HK的中点为(0,2),则M的中点为(0,2)∴P(-1,2);
②当MK为正方形的对角线时,如解图②,则MH⊥HK,PM∥KH,
∵HK∥y轴, ∴PM∥y轴,MH⊥y轴,
∴∠PMK=∠OBA=45°,MH∥x轴,
∴点H的纵坐标为2,∴-x2+2x+3=2,
解得x1= +1,x2=- +1,
即点H的横坐标为为 +1或- +1,
∴MH= ,
第3题解图②
∵四边形MHKP是正方形,
∴PM=MH= ,
又PM∥y轴,
∴点P的坐标为(1,2+ )或(1,2- ).
综上所述,点P的坐标为(5,2)或(-1,2)
或(1,2+ )或(1,2- ).
(3)(1,2+ )或(1,2- ).
第3题解图②
微专题 二次函数与矩形、菱形、正方形问题
微技能——分类讨论思想确定对应关系
一阶
一题多设问
设问突破
二阶
例1 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(5,0)两点,与y轴交于点C.点P是抛物线上一个动点,过点P作x轴的垂线,垂足为点H,交直线BC于点E.
例1题图①
(1)求抛物线的解析式;
例1题图①
(1)将A(1,0),B(5,0)代入y=-x2+bx+c中,
得
解得
∴抛物线解析式为y=-x2+6x-5 ;
(2)如图②,设点M是抛物线对称轴上一点,点N是平面内一点,是否存在点M,使得以B,C,M,N为顶点的四边形是矩形?若存在,求出点M的坐标;若不存在,请说明理由;
【思维教练】要求使得以B,C,M,N为顶点的四边形是矩形的点M的坐标,已知点M是抛物线对称轴上一点,设点M的坐标,分别求出BC,BM,CM的长,然后根据矩形的性质分别讨论∠CBM,∠BCM,∠CMB为直角的情况,利用勾股定理列方程求解.
例1题图②
M
N
(2)存在.
易得抛物线对称轴为直线x=3,
∵点M是对称轴上一点,设点M的坐标为(3,m),
易得BC2=52+52=50,BM2=(5-3)2+m2=4+m2,
①如解图①,连接CM,CM2=32+(m+5)2=m2+10m+34,
例1题解图①
若∠CBM=90°,
则BC2+BM2=CM2,
即50+4+m2=m2+10m+34, 解得m=2,
此时点M的坐标为(3,2);
M
N
②如解图②, 若∠BCM=90°.
则BC2+CM2=BM2,
即50+m2+10m+34=4+m2,
解得m=-8,
此时点M的坐标为(3,-8);
M
N
例1题解图②
③如解图③④,若∠BMC=90°.
则BM2+CM2=BC2,
即4+m2+m2+10m+34=50,
解得m=1或m=-6,
此时点M的坐标为(3,1)或(3,-6).
综上所述,满足条件的点M坐标为(3,2)或(3,-8)或(3,1)或(3,-6);
M
M
N
N
例1题解图③
例1题解图④
(3)如图③,点Q是平面直角坐标系内一点,当以点P,E,B,Q为顶点的四边形为菱形时,请求出此时点Q的坐标.
例1题图③
例1题图③
【思维教练】设点P的坐标为(x,-x2+6x-5),则点E的坐标为(x,x-5),共分为四种情况讨论:①当PH=HE,QH=HB时,四边形PQEB是菱形;②当点P在x轴上方,且PE=EB=BQ=QP时,四边形PEBQ为菱形;③当点P与点A重合,且PB=PE=EQ=QB时,四边形PEQB是菱形;④当点P在x轴下方,且PE=EB=BQ=QP时,四边形PEBQ为菱形.
例1题图③
(3)设点P的坐标为(x,-x2+6x-5)
设直线BC的解析式为y=kx+b(k≠0);
将B(5,0),C(0,5)代入得
解得
∴直线BC的解析式为y=x-5,则点E的坐标为(x,x-5),
例1题解图⑤
如解图⑤
∵PE⊥QB,
∴当PH=HE,QH=HB时,四边形PQEB是菱形.
此时yP=-yE,即-x2+6x-5=-(x-5),
解得x1=2,x2=5(不合题意,舍去),
∴QH=HB=3,
∴点Q的坐标为(-1,0);
例1题解图⑥
如解图⑥,当点P在x轴上方,
且PE=EB=BQ=QP时,四边形PEBQ为菱形.
∵PE=-x2+6x-5-(x-5)=-x2+5x,BE= BH= (5-x),
∴-x2+5x= (5-x),
解得x1=5(不合题意,舍去),x2= .
当x= 时,BQ=PE= ,
∴点Q的坐标为(5, );
例1题解图⑦
如解图⑦,当点P与点A重合时,PB=PE.
∴当PB=PE=EQ=QB时,四边形PEQB是菱形.
易得Q的坐标为(5,-4);
例1题解图⑧
如解图⑧,当点P在x轴下方,
且PE=EB=BQ=QP时,四边形PEBQ为菱形.
∵PE=x-5-(-x2+6x-5)=x2-5x,
BE= BH= (5-x),
∴x2-5x= (5-x),
解得x1=5(不合题意,舍去),x2=- .
当x=- 时,QB=PE= ,
∴点Q的坐标为(5, ).
综上所述,存在点Q,使得以点P,E,B,Q为顶点的四边形为菱形.此时点Q的坐标为(-1,0),(5, ),(5,-4)或(5, ).
(4)如图④,点M是抛物线的顶点,坐标平面内是否存在点P、Q(点P在点Q左侧),使得以B,M,P,Q为顶点的四边形是正方形?若存在,直接写出点P的坐标;若不存在,说明理由.
【思维教练】由BM为定边,可分以BM为正方形的边或以BM为正方形的对角线来确定点P.
例1题图④
【解法提示】当MB为正方形的边时,
①当点P在点M的左侧时,如解图⑨,
∵点M为抛物线的顶点,
∴M点坐标为(3,4),
∵B(5,0),
∴BM= ,
∴BM=PM= ,
设P1(m,n),过点P1作P1N1⊥x轴于点N1,
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
∴BN1=5-m,P1N1=n,
∴P1O= ,
P1B= ,
P1M= ,
解得m=-1,n=2,
∴P1(-1,2);
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
②当点P在点M右侧时,如解图⑨,
∵点P2与点P1关于直线BM对称,
∴P2(3×2+1,4×2-2),即P2(7,6);
当MB为正方形的对角线时,
∵点P在点Q左侧,
∴点P只能在点M的左侧,如解图⑨,
∵BM= ,
∴P3B=PM= ,
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
设P3(m,n),
∴P3B= ,
P3M= ,
解得m=2n,
∵点P3与点Q3关于直线MB对称,
∴Q3(5+n,5-m), ,
∴3n=3,n=1,∴m=2n=2,∴P3(2,1),
综上所述,存在点P,使得以B,M,P,Q为顶点的四边形为正方形,此时点P的坐标为(-1,2),(7,6),(2,1).
例1题解图⑨
P1
P2
P3
Q1
Q2
Q3
N2
N1
综合训练
三阶
第1题图
1. (2023抚本铁辽葫定心卷)如图,抛物线y=ax2+x+c(a≠0)交 x轴于点A(4,0)、B,交 y轴于点C(0,4).
(1)求抛物线的解析式;
(1)∵抛物线y=ax2+x+c(a≠0)
经过A(4,0),C(0,4)两点,
∴c= 解得
∴抛物线的解析式为y=- x2+x+4;
(2)∵点E是OA的中点,∴E(2,0).
由题意易知直线CE的解析式为y=-2x+4.
∵直线MN到y轴的距离为 ,
∴点D的坐标为( ,0)或(- ,0).
当D( ,0)时,点M、N的横坐标为 ,
将x= 代入y=-2x+4中,得y=1,
(2)如图①,点E是OA的中点,点D是线段BE上一点(不与点B、E重合),过点D作x轴的垂线,交直线CE于点M,交抛物线于点N,若直线MN到y轴的距离为 ,求点M与点N之间的距离;
第1题图
将x= 代入y=- x2+x+4中,得y= .
∴M( ,1),N( ),
∴MN= ;
当D(- ,0)时,点M、N的横坐标为- ,
将x=- 代入y=-2x+4中,得y=7,
将x=- 代入y=- x2+x+4中,得y= .
第1题图
∴M(- ,7),N(- , ),
∴MN=7- = .
∴点M与点N之间的距离为 或 ;
第1题图
第1题图
(3)如图②,点F在抛物线的对称轴上且在x轴上方,点G在坐标平面内,当以点B、C、F、G为顶点的四边形为菱形时,请直接写出点F的坐标.
【解法提示】已知抛物线解析式为y=- x2+x+4,
令y=0,即- x2+x+4=0,解得x1=-2,x2=4,
∴B(-2,0),抛物线的对称轴为直线x=1.
设点F的坐标为(1,m).
∵C(0,4),
∴BC2=OB2+OC2=20,BF2=9+m2 ,CF2=1+(m-4)2 .
要使以点B、C、F、G为顶点的四边形为菱形,分两种情况讨论,
当BC为菱形的边时,
①当BC=BF时,即20=9+m2 ,
解得m1= ,m2=- (不符合题意,舍去),
∴点F的坐标为(1, );
②当BC=CF时,
即20=1+(m-4)2,
解得m3=4+ ,m4=4- (不符合题意,舍去),
∴点F的坐标为(1,4+ );
第1题图
当BC为菱形的对角线时,则点F在线段BC的垂直平分线上.
∴BF=CF,
即9+m2=1+(m-4)2,
解得m=1.
∴点F的坐标为(1,1),
综上所述,点F的坐标为(1, )或(1,4+ )
或(1,1).
(3)点F的坐标为(1, )或(1,4+ )或(1,1).
第1题图
2. 如图,已知抛物线y=ax2-2ax+b与x轴交于点A(-2,0)和点B,与y轴交于点C(0,4).
(1)求抛物线的解析式;
第2题图
备用图
解:(1)将点A、C的坐标分别代入抛物线的解析式,
得 解得
∴抛物线的解析式为y= x2+x+4;
(2)点P是第四象限抛物线上一点,连接AC、AP,当∠PAB=2∠ACO时,求点P的坐标;
(2)如解图,在OB上取一点R,使OR=OA=2,连接CR,
则∠ACR=2∠ACO=∠PAB,
过点A作AK⊥CR于点K,设直线AP交y轴于点H,
H
R
第2题图
在y=- x2+x+4中,令y=0,
即- x2+x+4=0,
解得x1=-2(舍去),x2=4,
∴B(4,0).
K
∵A(-2,0),C(0,4),
∴AR=4,OC=4,AC=CR=
∴S△ACR= AR·OC= CR·AK,
即 ×4×4= 解得AK= ,
∴CK= ,
∴tan∠ACK=
H
R
第2题图
K
∵∠PAB=2∠ACO=∠ACK,
∴tan∠ACK=tan∠PAB.
在Rt△AOH中,OH=OA·tan∠PAB= .
∴H(0, ).
由点A、H的坐标得直线AP的解析式为y= .
联立 解得 或 (舍去),
∴点P的坐标为( );
H
R
第2题图
K
(3)点M是抛物线的对称轴上一动点,在平面内是否存在点N,使得以M、N、B、C为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
第2题图
【解法提示】∵y= x2+x+4,
∴抛物线的对称轴为直线x=1.
设点M的坐标为(1,m),
∵B(4,0),C(0,4),
∴BM2=9+m2,CM2=m2-8m+17,BC2=32.
当以M、N、B、C为顶点的四边形是矩形时,需分以BC为边和BC为对角线两种情况讨论.
①当BC为边时,以M、B、C为顶点的三角形是以BC为直角边的直角三角形,则分以MC为斜边和以MB为斜边,
当以MC为斜边时,BC2+BM2=CM2,即32+9+m2=m2-8m+17,解得m=-3,
∴点M的坐标为(1,-3).
由xC+xM=xB+xN,得xN=-3,同理可得yN=1,
∴点N的坐标为(-3,1);
第2题图
当以MB为斜边时,
BC2+CM2=BM2,即32+m2-8m+17=m2+9,
解得m=5,∴M(1,5).
由xB+xM=xC+xN,得xN=5,
同理可得yN=1,∴点N的坐标为(5,1);
②当以BC为对角线时,以M、B、C为顶点的三角形是以BC为斜边的直角三角形,则BM2+CM2=BC2,即9+m2+m2-8m+17=32,
解得m1=2+ ,m2=2- ,
∴点M的坐标为(1,2+ )或(1,2- ),
第2题图
由xB+xC=xM+xN,得xN=3,
同理可得yN=2- 或2+ ,
∴点N的坐标为(3,2- )或(3,2+ ).
综上所述,存在点N
使得以M、N、B、C为顶点的四边形是矩形,满足条件的点N的坐标为(-3,1)或(5,1)或(3,2- )或(3,2+ ).
(3)存在,点N的坐标为(-3,1)或(5,1)或(3,2- )或(3,2+ ).
第2题图
3. 直线y=-x+3与x轴相交于点A,与y轴相交于点B,抛物线y=ax2+2x+c经过点A,B,与x轴的另一个交点为C.
(1)求抛物线的解析式;
第3题图①
备用图
(1)在y=-x+3中,令y=0,则x=3,
令x=0,则y=3,
∴A(3,0),B(0,3),
把A(3,0),B(0,3)代入y=ax2+2x+c得, ∴
∴抛物线的解析式为y=-x2+2x+3;
(2)如图①,点D是第一象限内抛物线上的一个动点,过点D作DE∥y轴交AB于点E,DF⊥AB于点F,FG⊥x轴于点G,当DE=FG时,求点D的坐标;
第3题图①
由(1)可知抛物线的解析式为y=-x2+2x+3,
直线AB的解析式为y=-x+3,
设D(m,-m2+2m+3),
∵DE∥y轴,∴E(m,-m+3),
∴DE=-m2+2m+3-(-m+3)=-m2+3m,ME=-m+3,
(2)如解图,延长DE交x轴于点M,则DM⊥x轴
M
∵B(0,3),A(3,0)∴OB=OA=3,∴∠OBA=∠OAB=45°,
∵DM⊥x轴,DF⊥AB,∴∠DEF=∠AEM=45°,
∴DE= EF,AF= FG,
∵DE=FG,∴AF=2EF,∴AE=EF,
∵FG⊥x轴,∴FG∥ME,
∴ ∴FG=2ME,
∴DE=2ME,∴-m2+3m=2(-m+3),
∴m=2或m=3(舍去),
∴D(2,3);
第3题图①
M
(3)如图②,在(2)的条件下,直线CD与AB相交于点M,点H在抛物线上,过点H作HK∥y轴,交直线CD于点K.P是平面内一点,当以点M,H,K,P为顶点的四边形是正方形时,请直接写出点P的坐标.
第3题图②
【解法提示】在y=-x2+2x+3中,令y=0,则-x2+2x+3=0,
解得x=-1或x=3,∴点C的坐标为(-1,0),
设直线CD的解析式为y=kx+b,根据题意得
解得 ,
∴直线CD的解析式为y=x+1.
联立直线CD与直线AB的解析式得 解得
∴点M的坐标为(1,2).
①当MK为正方形边时,则MH⊥MK时,
H点在AB上,K点在CD上.
∵H点在抛物线上,∴H(3,0)或H(0,3);
当H(3,0)时,MH= ,∴KH=4,
∴K(3,4)
∴HK的中点为(3,2),则MP的中点为(3,2);
∴P(5,2);
第3题图②
当H(0,3)时,MH= ,∴KH=2,∴K(0,1),
∴HK的中点为(0,2),则M的中点为(0,2)∴P(-1,2);
②当MK为正方形的对角线时,如解图②,则MH⊥HK,PM∥KH,
∵HK∥y轴, ∴PM∥y轴,MH⊥y轴,
∴∠PMK=∠OBA=45°,MH∥x轴,
∴点H的纵坐标为2,∴-x2+2x+3=2,
解得x1= +1,x2=- +1,
即点H的横坐标为为 +1或- +1,
∴MH= ,
第3题解图②
∵四边形MHKP是正方形,
∴PM=MH= ,
又PM∥y轴,
∴点P的坐标为(1,2+ )或(1,2- ).
综上所述,点P的坐标为(5,2)或(-1,2)
或(1,2+ )或(1,2- ).
(3)(1,2+ )或(1,2- ).
第3题解图②
同课章节目录
