2024辽宁中考数学二轮专题复习 微专题 二次函数与相似三角形问题 课件(共33张PPT)
文档属性
| 名称 | 2024辽宁中考数学二轮专题复习 微专题 二次函数与相似三角形问题 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 366.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 20:38:34 | ||
图片预览




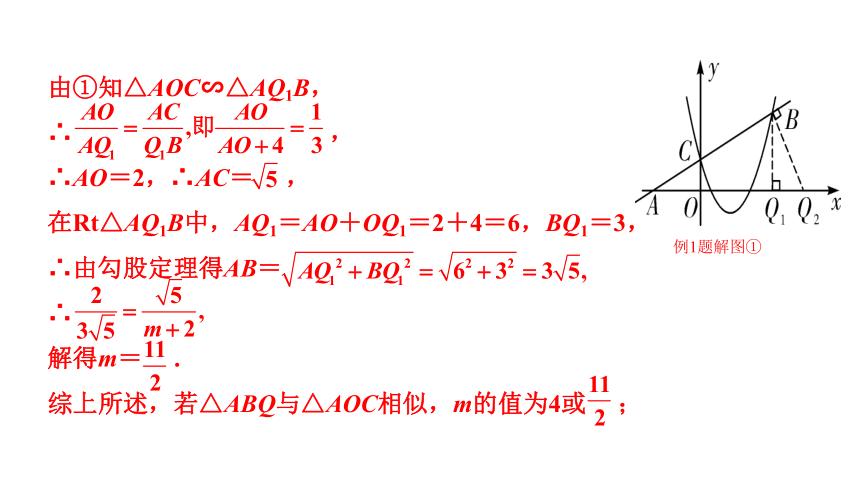




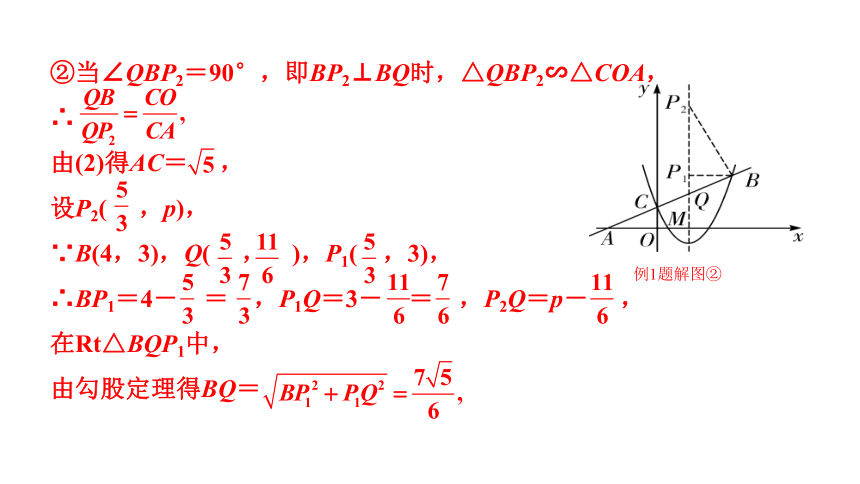

文档简介
(共33张PPT)
在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2- x+c与直线AC交于点B(4,3).
例 1
微技能——分类讨论思想确定对应关系
一阶
一题多设问
微专题 二次函数与相似三角形问题(含全等)
一题多设问
二阶
见微专题 相似三角形的对应关系不确定
解:(1)∵直线y=kx+1与y轴交于点C,
∴点C的坐标为(0,1).
∵抛物线y=ax2- x+c过C(0,1),B(4,3),
∴
∴抛物线的表达式为y= x2- x+1;
(1)求抛物线的表达式;
例1题图①
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求m的值;
【思维教练】已知点Q的坐标,即可用m表示出AQ的长,由于未说明两三角形相似的对应关系,要考虑两种情况:①当点C的对应点是点B时;②当点C的对应点是点Q时,然后利用三角形相似的性质得到对应边成比例,从而列关于m的方程即可求解.
例1题图②
(2)如解图①,分两种情况讨论,
①当点C的对应点是点B时,过点B作BQ1⊥x轴于点Q1,
∵BQ1∥CO,
∴△AOC∽△AQ1B,
此时点Q1的坐标为(4,0),即m的值为4;
②当点C的对应点是点Q2时,过点B作BQ2⊥AB,交x轴于点Q2,
∵∠CAO=∠Q2AB,∠AOC=∠ABQ2=90°,
∴△AOC∽△ABQ2,
∴ ,
例1题解图①
由①知△AOC∽△AQ1B,
∴ ,
∴AO=2,∴AC= ,
在Rt△AQ1B中,AQ1=AO+OQ1=2+4=6,BQ1=3,
∴由勾股定理得AB=
∴
解得m= .
综上所述,若△ABQ与△AOC相似,m的值为4或 ;
例1题解图①
(3)设抛物线的对称轴与BC相交于点Q,点P是抛物线对称轴上的动点,且点P不与点Q重合,是否存在点P,使得以P、B、Q为顶点的三角形与△AOC相似?若存在,求出点P的坐标;若不存在,请说明理由;
例1题图③
【思维教练】由已知条件可知△AOC是直角三角形,所以△BPQ一定也是直角三角形,故点P一定在点Q的上方.在△AOC和△BPQ中,∠ACO=∠BQP,所以只需要在△BPQ中确定一个直角即可.分情况考虑:①∠BPQ=90°;②∠QBP=90°,
再分别求解,点P的坐标即可求出.
例1题图③
例1题图③
(3)存在,
∵C(0,1),B(4,3)在直线y=kx+1上,∴代入得k= ,
∴直线AC的表达式为y= x+1,
由抛物线的表达式y= x2- x+1得对称轴为直线x= ,
∵点Q在直线AC上,
∴将x= 代入y= x+1中,
得y= ,
∴点Q的坐标为( , ),
如解图②,设直线x= 与x轴的交点为点M,
则OC∥QM,
∴∠OCA=∠MQA=∠BQP,
又∵∠AOC=90°,
∴要分为两种情况:
①当∠BP1Q=90°,即BP1∥x轴时,△BP1Q∽△AOC,
∵点B的坐标为(4,3),
∴点P1的坐标为( ,3);
例1题解图②
②当∠QBP2=90°,即BP2⊥BQ时,△QBP2∽△COA,
∴
由(2)得AC= ,
设P2( ,p),
∵B(4,3),Q( , ),P1( ,3),
∴BP1=4- = ,P1Q=3- = ,P2Q=p- ,
在Rt△BQP1中,
由勾股定理得BQ=
例1题解图②
例1题解图②
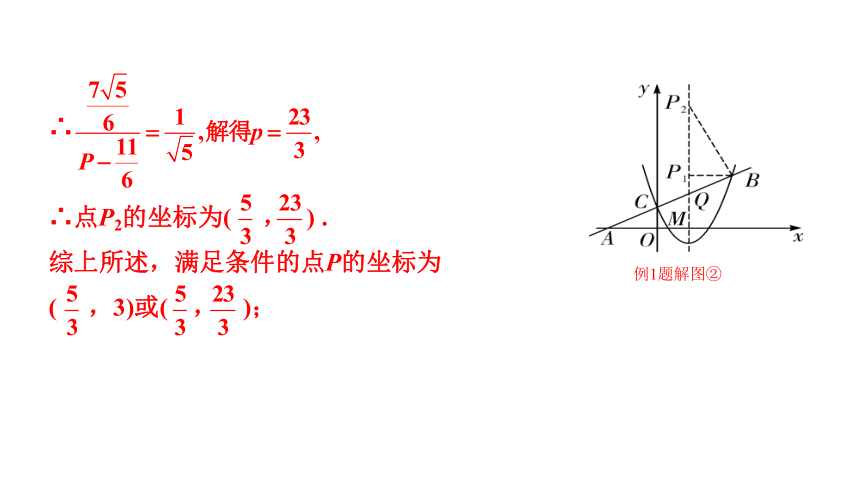
∴
∴点P2的坐标为( , ) .
综上所述,满足条件的点P的坐标为
( ,3)或( , );
(4)连接BO,点S是抛物线CB段上的动点,过点S作SK∥x轴,交BO于点K,是否存在点S,使得△AOB∽△SKO?若存在,求出点S的坐标;若不存在,请说明理由.
例1题图④
【思维教练】由△AOB∽△SKO得∠AOB=∠SKO,即点S在点K的右侧,再由△AOB∽△SKO,得∠ABO=∠SOK,从而得到OS∥AB,由(2)可得AB的表达式,再平移得到OS的表达式,然后与抛物线表达式联立解方程即可求出点S的坐标.
(4)存在.
理由如下:∵△AOB∽△SKO,
∴∠AOB=∠SKO,
∴点S在点K的右侧,
由△AOB∽△SKO,
得∠ABO=∠SOK,
∴OS∥AB,
∴直线OS的表达式为y= x,
例1题图④
∴综上所述,满足条件的点S的坐标为(2- ,1- )或(2+ , 1+ ).
例1题图④
综合训练
三阶
1. 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,抛物线的顶点为D.
第1题图
(1)求抛物线的解析式及点D的坐标;
解:(1)∵A(-1,0),B(3,0),a=1,
∴抛物线的解析式为y=(x+1)(x-3)=x2-2x-3=(x-1)2-4,
∴点D的坐标为(1,-4);
(2)连接BC、BD、CD,求△BCD的面积;
(2)如解图,当x=0时,y=-3,
∴C(0,-3).
∵D(1,-4),
∴BC= ,CD= ,
BD=
∵BC2+CD2=18+2=20=BD2,
∴△BCD是直角三角形,且∠BCD=90°.
∴S△BCD= BC·CD= ×3 × =3;
第1题图
(3)点E在y轴上,且DE=EB,点P在直线DE上,当△BEP与△BOE相似时,请直接写出所有满足条件的点P的坐标.
【解法提示】设点E的坐标为(0,m),
∴BE2=OE2+OB2=m2+9.
如解图②,过点D作DF⊥y轴于点F,
∴DE2=EF2+DF2=(m+4)2+1.
∵DE=EB,
∴(m+4)2+1=m2+9,
第1题解图②
第1题图
解得m=-1,
∴点E的坐标为(0,-1).
∵D(1,-4)
∴DE所在的直线表达式为y=-3x-1,
∵点B(3,0),
∴BO=EF=3,EO=DF=1,
根据勾股定理,得BE= ,
∵∠BOE=∠EFD=90°,
∴△BOE≌△EFD,
第1题解图②
∴∠DEF=∠EBO.
又∵∠EBO+∠BEO=90°,
∴∠DEF+∠BEO=90°,
∴∠BED=180°-90°=90°,
∴DE⊥BE.
①当OB与EB是对应边时,
∵△BOE∽△BEP,
∴ ∴EP= .
第1题解图②
如解图②,过点P作PG⊥y轴于点G,易得△EGP∽△EFD,
∴EG= EF=1,PG= DF= .
当点P在点E的左边时,OG=EG-EO=1-1=0,
∴代入直线DE∶y=-3x-1,得x=- ,
∴点P(- ,0);
当点P在点E的右边时,OG=EO+EG=1+1=2,
∴代入直线DE∶y=-3x-1,得x= ,∴点P( ,-2);
第1题解图②
②当OB与EP是对应边时,
∵△BOE∽△PEB,
∴
∴EP= .
过点P作PG⊥y轴于点G,
∵△EPG∽△EDF,
∴
∴EG=3EF=9,PG=3DF=3.
当点P在点E的左边时,OG=EG-OE=9-1=8,
第1题解图②
(3)点P的坐标为(- ,0)或( ,-2)或(-3,8)或(3,-10).
∴代入直线DE:y=-3x-1,得x=-3,
∴点P(-3,8);
当点P在点E的右边时,OG=OE+EG=1+9=10,
∴代入直线DE得:y=-3x-1,x=3,
∴点P(3,-10).
综上所述,满足条件的点P的坐标为(- ,0)或( ,-2)或(-3,8)或(3,-10).
第1题解图②
2. 如图,抛物线y= x2+bx+c与x轴交于A(-8,0)、B(2,0)两点,与y轴交于点C,点D为抛物线上第三象限内的一个动点,连接AC,AD,DC,BC.
第2题图
(1)求抛物线的函数表达式及点C的坐标;
解:(1)将A(-8,0)、B(2,0)代入y= x2+bx+c中,
∴抛物线的表达式为y= x2+ x-4.
当x=0时,y=-4,
∴点C的坐标为(0,-4);
第2题图
(2)当四边形ABCD的面积为36时,求点D的坐标;
∵A(-8,0),B(2,0),C(0,-4),
∴AB=10,OC=4.
∴S△ABC= AB·OC= ×10×4=20.
∴S△ADC=S四边形ABCD-S△ABC=36-20=16.
第2题图
G
H
(2)如解图,过点D作DG⊥AB交AB于点G,交AC于点H.
设直线AC的表达式为y=kx+d(k≠0),
将A(-8,0),C(0,-4)代入,得
∴直线AC的表达式为y=- x-4.
第2题图
G
H
设D(x, x2+ x-4)(-8<x<0),
则H(x,- x-4),
∴DH=yH-yD=(- x-4)-( x2+ x-4)
=- x2-2x,
∴S△ADC= DH·OA= ×(- x2-2x)×8
=-x2-8x=16,
解得x1=x2=-4,
代入抛物线得y=-6,
∴点D的坐标为(-4,-6);
第2题图
G
H
(3)在(2)的条件下,平面内是否存在点M(不与点C重合),使得以点A,D,M为顶点的三角形与△ACD全等?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【解法提示】由题意,当以点A,D,M为
顶点的三角形与△ACD全等时,
可分两种情况进行讨论:
①当△ACD △AMD时,
CD=MD,AC=AM.
∵A(-8,0),C(0,-4),D(-4,-6)
≌
第2题图
G
H
∴直线AD的表达式为y=- x-12.
∵△ACD △AMD,
∴点C与点M关于直线AD对称,
∴直线CM⊥AD.
∴直线CM的表达式y= x-4.
≌
设直线AD的表达式为y=k1x+b1(k1≠0),将A(-8,0),D(-4,-6)代入得
第2题图
G
H
∴线段CM中点的坐标为(- ,- ).
设点M的坐标为(m,n),
∴
∴点M1的坐标为(- , ).
第2题图
G
H
②当△ACD △DMA时,
Ⅰ.当点M在AD的下方时,MA=CD,∠MAD=∠CDA.
∴MA∥CD.
∵A(-8,0),C(0,-4),D(-4,-6),
∴点M2的坐标为(-12,-2);
Ⅱ.当点M在AD的上方时,
此时M1M3与AD互相平分.
∵A(-8,0),D(-4,-6),
∴AD中点的坐标为(-6,-3).
≌
第2题图
G
H
设M3的坐标为(m3,n3),
∴
∴M3坐标为(- , ).
综上所述,存在点M使得以A,D,M为
顶点的三角形与△ACD全等,此时点M的
坐标为(- , )或(-12,-2)或(- , ).
第2题图
G
H
(3)存在,点M的坐标为(- ,- )或(-12,-2)或(- , ).
第2题图
G
H
在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2- x+c与直线AC交于点B(4,3).
例 1
微技能——分类讨论思想确定对应关系
一阶
一题多设问
微专题 二次函数与相似三角形问题(含全等)
一题多设问
二阶
见微专题 相似三角形的对应关系不确定
解:(1)∵直线y=kx+1与y轴交于点C,
∴点C的坐标为(0,1).
∵抛物线y=ax2- x+c过C(0,1),B(4,3),
∴
∴抛物线的表达式为y= x2- x+1;
(1)求抛物线的表达式;
例1题图①
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求m的值;
【思维教练】已知点Q的坐标,即可用m表示出AQ的长,由于未说明两三角形相似的对应关系,要考虑两种情况:①当点C的对应点是点B时;②当点C的对应点是点Q时,然后利用三角形相似的性质得到对应边成比例,从而列关于m的方程即可求解.
例1题图②
(2)如解图①,分两种情况讨论,
①当点C的对应点是点B时,过点B作BQ1⊥x轴于点Q1,
∵BQ1∥CO,
∴△AOC∽△AQ1B,
此时点Q1的坐标为(4,0),即m的值为4;
②当点C的对应点是点Q2时,过点B作BQ2⊥AB,交x轴于点Q2,
∵∠CAO=∠Q2AB,∠AOC=∠ABQ2=90°,
∴△AOC∽△ABQ2,
∴ ,
例1题解图①
由①知△AOC∽△AQ1B,
∴ ,
∴AO=2,∴AC= ,
在Rt△AQ1B中,AQ1=AO+OQ1=2+4=6,BQ1=3,
∴由勾股定理得AB=
∴
解得m= .
综上所述,若△ABQ与△AOC相似,m的值为4或 ;
例1题解图①
(3)设抛物线的对称轴与BC相交于点Q,点P是抛物线对称轴上的动点,且点P不与点Q重合,是否存在点P,使得以P、B、Q为顶点的三角形与△AOC相似?若存在,求出点P的坐标;若不存在,请说明理由;
例1题图③
【思维教练】由已知条件可知△AOC是直角三角形,所以△BPQ一定也是直角三角形,故点P一定在点Q的上方.在△AOC和△BPQ中,∠ACO=∠BQP,所以只需要在△BPQ中确定一个直角即可.分情况考虑:①∠BPQ=90°;②∠QBP=90°,
再分别求解,点P的坐标即可求出.
例1题图③
例1题图③
(3)存在,
∵C(0,1),B(4,3)在直线y=kx+1上,∴代入得k= ,
∴直线AC的表达式为y= x+1,
由抛物线的表达式y= x2- x+1得对称轴为直线x= ,
∵点Q在直线AC上,
∴将x= 代入y= x+1中,
得y= ,
∴点Q的坐标为( , ),
如解图②,设直线x= 与x轴的交点为点M,
则OC∥QM,
∴∠OCA=∠MQA=∠BQP,
又∵∠AOC=90°,
∴要分为两种情况:
①当∠BP1Q=90°,即BP1∥x轴时,△BP1Q∽△AOC,
∵点B的坐标为(4,3),
∴点P1的坐标为( ,3);
例1题解图②
②当∠QBP2=90°,即BP2⊥BQ时,△QBP2∽△COA,
∴
由(2)得AC= ,
设P2( ,p),
∵B(4,3),Q( , ),P1( ,3),
∴BP1=4- = ,P1Q=3- = ,P2Q=p- ,
在Rt△BQP1中,
由勾股定理得BQ=
例1题解图②
例1题解图②
∴
∴点P2的坐标为( , ) .
综上所述,满足条件的点P的坐标为
( ,3)或( , );
(4)连接BO,点S是抛物线CB段上的动点,过点S作SK∥x轴,交BO于点K,是否存在点S,使得△AOB∽△SKO?若存在,求出点S的坐标;若不存在,请说明理由.
例1题图④
【思维教练】由△AOB∽△SKO得∠AOB=∠SKO,即点S在点K的右侧,再由△AOB∽△SKO,得∠ABO=∠SOK,从而得到OS∥AB,由(2)可得AB的表达式,再平移得到OS的表达式,然后与抛物线表达式联立解方程即可求出点S的坐标.
(4)存在.
理由如下:∵△AOB∽△SKO,
∴∠AOB=∠SKO,
∴点S在点K的右侧,
由△AOB∽△SKO,
得∠ABO=∠SOK,
∴OS∥AB,
∴直线OS的表达式为y= x,
例1题图④
∴综上所述,满足条件的点S的坐标为(2- ,1- )或(2+ , 1+ ).
例1题图④
综合训练
三阶
1. 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,抛物线的顶点为D.
第1题图
(1)求抛物线的解析式及点D的坐标;
解:(1)∵A(-1,0),B(3,0),a=1,
∴抛物线的解析式为y=(x+1)(x-3)=x2-2x-3=(x-1)2-4,
∴点D的坐标为(1,-4);
(2)连接BC、BD、CD,求△BCD的面积;
(2)如解图,当x=0时,y=-3,
∴C(0,-3).
∵D(1,-4),
∴BC= ,CD= ,
BD=
∵BC2+CD2=18+2=20=BD2,
∴△BCD是直角三角形,且∠BCD=90°.
∴S△BCD= BC·CD= ×3 × =3;
第1题图
(3)点E在y轴上,且DE=EB,点P在直线DE上,当△BEP与△BOE相似时,请直接写出所有满足条件的点P的坐标.
【解法提示】设点E的坐标为(0,m),
∴BE2=OE2+OB2=m2+9.
如解图②,过点D作DF⊥y轴于点F,
∴DE2=EF2+DF2=(m+4)2+1.
∵DE=EB,
∴(m+4)2+1=m2+9,
第1题解图②
第1题图
解得m=-1,
∴点E的坐标为(0,-1).
∵D(1,-4)
∴DE所在的直线表达式为y=-3x-1,
∵点B(3,0),
∴BO=EF=3,EO=DF=1,
根据勾股定理,得BE= ,
∵∠BOE=∠EFD=90°,
∴△BOE≌△EFD,
第1题解图②
∴∠DEF=∠EBO.
又∵∠EBO+∠BEO=90°,
∴∠DEF+∠BEO=90°,
∴∠BED=180°-90°=90°,
∴DE⊥BE.
①当OB与EB是对应边时,
∵△BOE∽△BEP,
∴ ∴EP= .
第1题解图②
如解图②,过点P作PG⊥y轴于点G,易得△EGP∽△EFD,
∴EG= EF=1,PG= DF= .
当点P在点E的左边时,OG=EG-EO=1-1=0,
∴代入直线DE∶y=-3x-1,得x=- ,
∴点P(- ,0);
当点P在点E的右边时,OG=EO+EG=1+1=2,
∴代入直线DE∶y=-3x-1,得x= ,∴点P( ,-2);
第1题解图②
②当OB与EP是对应边时,
∵△BOE∽△PEB,
∴
∴EP= .
过点P作PG⊥y轴于点G,
∵△EPG∽△EDF,
∴
∴EG=3EF=9,PG=3DF=3.
当点P在点E的左边时,OG=EG-OE=9-1=8,
第1题解图②
(3)点P的坐标为(- ,0)或( ,-2)或(-3,8)或(3,-10).
∴代入直线DE:y=-3x-1,得x=-3,
∴点P(-3,8);
当点P在点E的右边时,OG=OE+EG=1+9=10,
∴代入直线DE得:y=-3x-1,x=3,
∴点P(3,-10).
综上所述,满足条件的点P的坐标为(- ,0)或( ,-2)或(-3,8)或(3,-10).
第1题解图②
2. 如图,抛物线y= x2+bx+c与x轴交于A(-8,0)、B(2,0)两点,与y轴交于点C,点D为抛物线上第三象限内的一个动点,连接AC,AD,DC,BC.
第2题图
(1)求抛物线的函数表达式及点C的坐标;
解:(1)将A(-8,0)、B(2,0)代入y= x2+bx+c中,
∴抛物线的表达式为y= x2+ x-4.
当x=0时,y=-4,
∴点C的坐标为(0,-4);
第2题图
(2)当四边形ABCD的面积为36时,求点D的坐标;
∵A(-8,0),B(2,0),C(0,-4),
∴AB=10,OC=4.
∴S△ABC= AB·OC= ×10×4=20.
∴S△ADC=S四边形ABCD-S△ABC=36-20=16.
第2题图
G
H
(2)如解图,过点D作DG⊥AB交AB于点G,交AC于点H.
设直线AC的表达式为y=kx+d(k≠0),
将A(-8,0),C(0,-4)代入,得
∴直线AC的表达式为y=- x-4.
第2题图
G
H
设D(x, x2+ x-4)(-8<x<0),
则H(x,- x-4),
∴DH=yH-yD=(- x-4)-( x2+ x-4)
=- x2-2x,
∴S△ADC= DH·OA= ×(- x2-2x)×8
=-x2-8x=16,
解得x1=x2=-4,
代入抛物线得y=-6,
∴点D的坐标为(-4,-6);
第2题图
G
H
(3)在(2)的条件下,平面内是否存在点M(不与点C重合),使得以点A,D,M为顶点的三角形与△ACD全等?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【解法提示】由题意,当以点A,D,M为
顶点的三角形与△ACD全等时,
可分两种情况进行讨论:
①当△ACD △AMD时,
CD=MD,AC=AM.
∵A(-8,0),C(0,-4),D(-4,-6)
≌
第2题图
G
H
∴直线AD的表达式为y=- x-12.
∵△ACD △AMD,
∴点C与点M关于直线AD对称,
∴直线CM⊥AD.
∴直线CM的表达式y= x-4.
≌
设直线AD的表达式为y=k1x+b1(k1≠0),将A(-8,0),D(-4,-6)代入得
第2题图
G
H
∴线段CM中点的坐标为(- ,- ).
设点M的坐标为(m,n),
∴
∴点M1的坐标为(- , ).
第2题图
G
H
②当△ACD △DMA时,
Ⅰ.当点M在AD的下方时,MA=CD,∠MAD=∠CDA.
∴MA∥CD.
∵A(-8,0),C(0,-4),D(-4,-6),
∴点M2的坐标为(-12,-2);
Ⅱ.当点M在AD的上方时,
此时M1M3与AD互相平分.
∵A(-8,0),D(-4,-6),
∴AD中点的坐标为(-6,-3).
≌
第2题图
G
H
设M3的坐标为(m3,n3),
∴
∴M3坐标为(- , ).
综上所述,存在点M使得以A,D,M为
顶点的三角形与△ACD全等,此时点M的
坐标为(- , )或(-12,-2)或(- , ).
第2题图
G
H
(3)存在,点M的坐标为(- ,- )或(-12,-2)或(- , ).
第2题图
G
H
同课章节目录
