2024辽宁中考数学二轮专题复习 微专题 二次函数与角度问题课件 57张PPT
文档属性
| 名称 | 2024辽宁中考数学二轮专题复习 微专题 二次函数与角度问题课件 57张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 900.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 21:10:56 | ||
图片预览




文档简介
(共57张PPT)
微技能——角的表示
一阶
例 1
一题多设问
已知抛物线交x轴于A、B两
点(点A在点B的左侧),与y轴交于点C,连接AC.
微专题 二次函数与角度问题
例1题图①
【作图依据】_______________________________________________
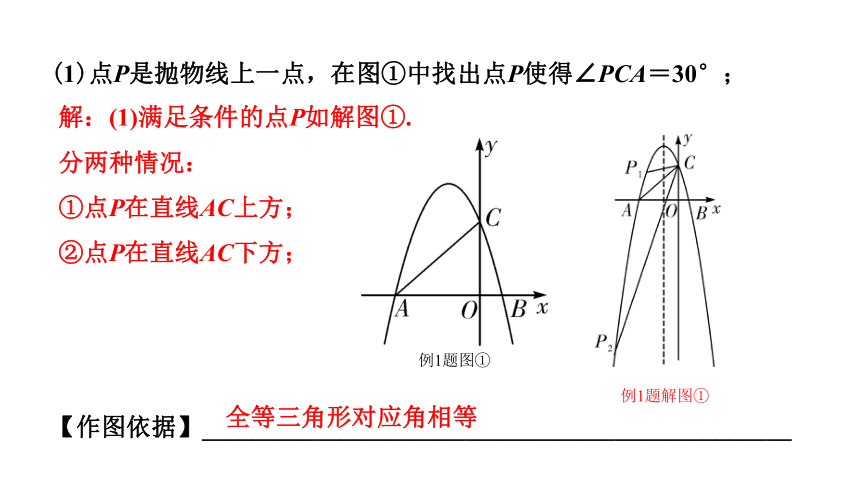
(1)点P是抛物线上一点,在图①中找出点P使得∠PCA=30°;
例1题图①
解:(1)满足条件的点P如解图①.
分两种情况:
①点P在直线AC上方;
②点P在直线AC下方;
全等三角形对应角相等
例1题解图①
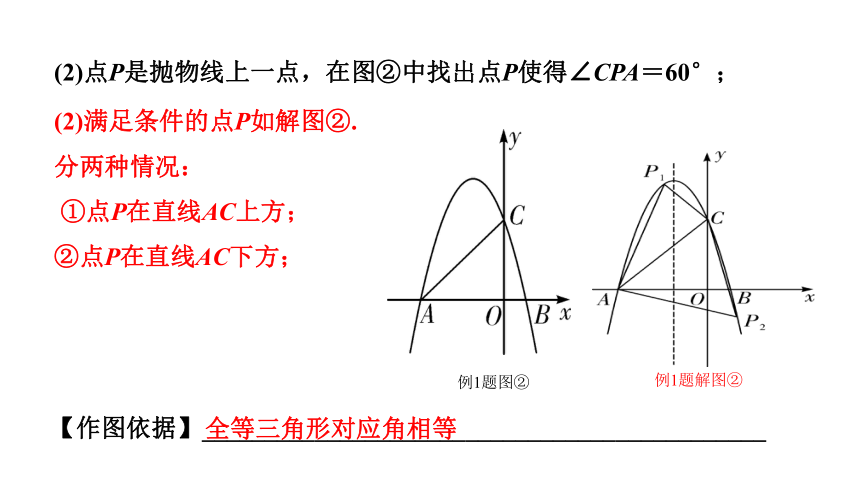
(2)点P是抛物线上一点,在图②中找出点P使得∠CPA=60°;
例1题图②
【作图依据】_____________________________________________
(2)满足条件的点P如解图②.
分两种情况:
①点P在直线AC上方;
②点P在直线AC下方;
例1题解图②
全等三角形对应角相等
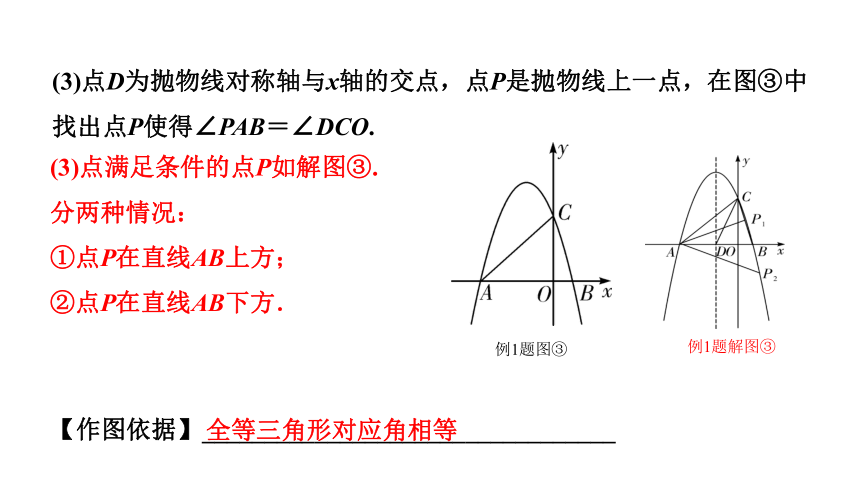
(3)点满足条件的点P如解图③.
分两种情况:
①点P在直线AB上方;
②点P在直线AB下方.
【作图依据】_________________________________
(3)点D为抛物线对称轴与x轴的交点,点P是抛物线上一点,在图③中找出点P使得∠PAB=∠DCO.
例1题图③
例1题解图③
全等三角形对应角相等
一题多设问
二阶
例 2
一题多设问
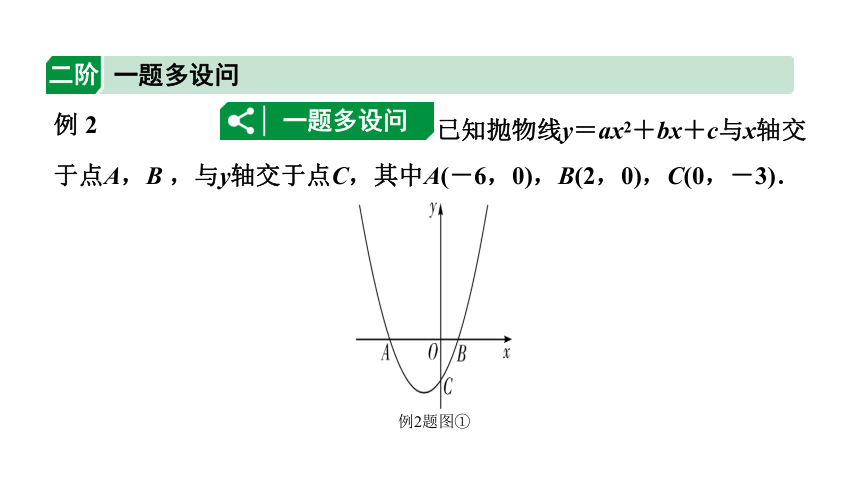
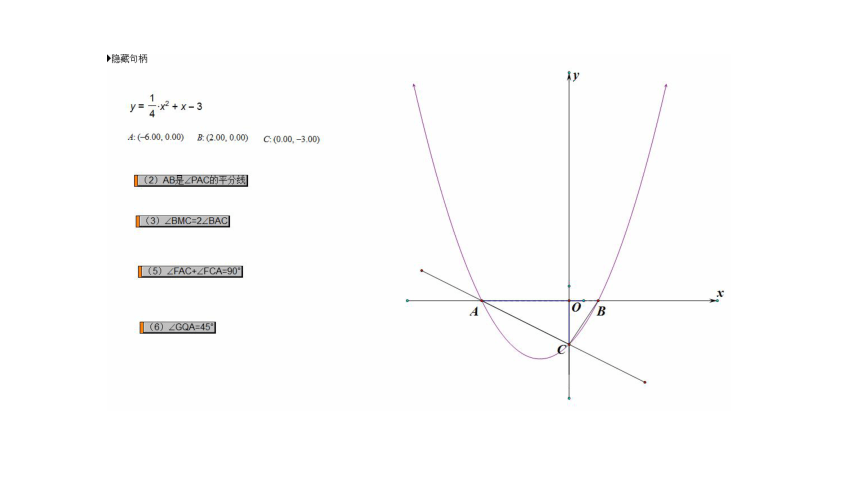
已知抛物线y=ax2+bx+c与x轴交于点A,B ,与y轴交于点C,其中A(-6,0),B(2,0),C(0,-3).
例2题图①
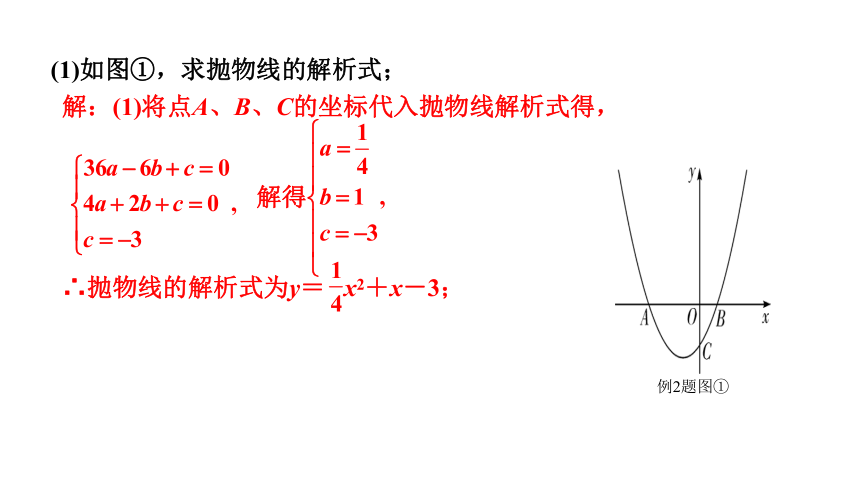
(1)如图①,求抛物线的解析式;
解:(1)将点A、B、C的坐标代入抛物线解析式得,
解得
∴抛物线的解析式为y= x2+x-3;
例2题图①
(2)如图②,在抛物线上是否存在一点P,使得AB为∠PAC的平分线?若存在,请直接写出点P的坐标;若不存在,请说明理由;
例2题图②
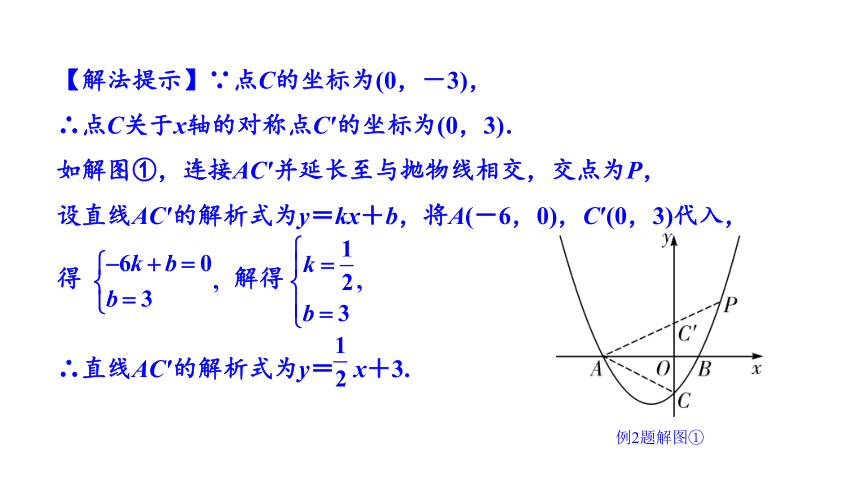
【思维教练】要求以AB为∠PAC的平分线的点P的坐标,根据角平分线的性质,作点C关于x轴的对称点C′,先求出直线AC′的解析式,再与抛物线解析式联立,即可得到点P的坐标.
【解法提示】∵点C的坐标为(0,-3),
∴点C关于x轴的对称点C′的坐标为(0,3).
如解图①,连接AC′并延长至与抛物线相交,交点为P,
设直线AC′的解析式为y=kx+b,将A(-6,0),C′(0,3)代入,
得 解得
∴直线AC′的解析式为y= x+3.
例2题解图①
联立
解得
∴点P的坐标为(4,5).
(2)存在,点P的坐标为(4,5);
例2题解图①
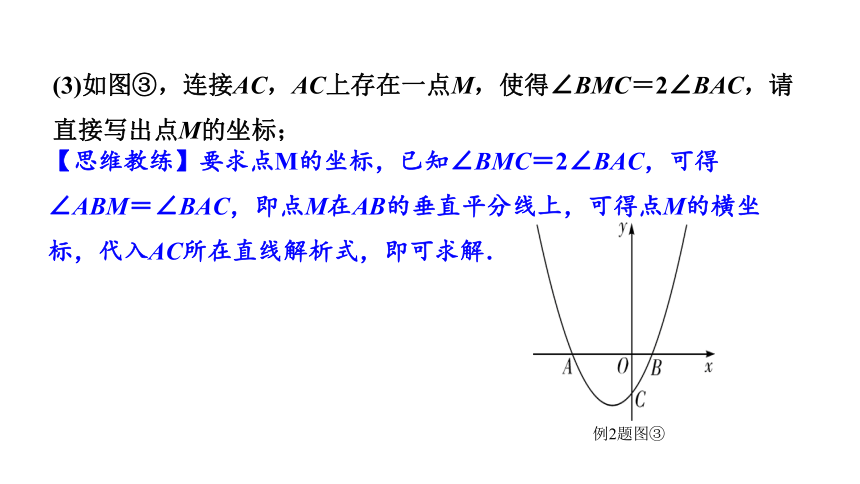
(3)如图③,连接AC,AC上存在一点M,使得∠BMC=2∠BAC,请直接写出点M的坐标;
【思维教练】要求点M的坐标,已知∠BMC=2∠BAC,可得∠ABM=∠BAC,即点M在AB的垂直平分线上,可得点M的横坐标,代入AC所在直线解析式,即可求解.
例2题图③
【解法提示】如解图②,过点M作x轴的垂线,垂足为N,连接AC,BM.
∵∠BMC=2∠BAC,∠BMC=∠BAC+∠ABM,
∴∠ABM=∠BAC,
∴AM=BM.
∵MN⊥AB,
∴AN=BN,
∴点M的横坐标为 =-2.
例2题解图②
设直线AC的解析式为y=kx+b(k≠0),将A(-6,0),C(0,-3)代入,
∴直线AC的解析式为y=- x-3.
将x=-2代入y=- x-3中得,y=-2,
∴点M的坐标为(-2,-2).
例2题解图③
(3)点M的坐标为(-2,-2);
(4)如图④,在抛物线上是否存在一点E,使得∠EBA=∠OCA?若存在,请直接写出点E的坐标;若不存在,请说明理由;
例2题图④
【思维教练】要求点E的坐标,已知∠EBA=∠OCA,过点E作EH⊥x轴于点H,则△HBE∽△OCA,设点E的坐标,代入比例关系可列方程求解.
【解法提示】设点E的坐标为(t, t2+t-3),如解图③,过点E作EH⊥x轴于点H,连接EB,AC,
∴H(t,0).
∵∠EBA=∠OCA,∠EHB=∠AOC=90°,
∴△HBE∽△OCA,
例2题解图③
E
H
解得 t1=2,t2=-14,
当t=2时, t2+t-3=0,不符合题意,舍去,
当t=-14时,t2+t-3=32,
∴E(-14,32).
(4)存在,点E的坐标为(-14,32);
例2题解图③
E
H
(5)如图⑤,在抛物线的对称轴上是否存在点F,使得∠FAC+∠FCA=90°?若存在,直接写出点F的坐标;如不存在,请说明理由;
例2题图⑤
【思维教练】要求点F的坐标,已知∠FAC+∠FCA=90°可得∠AFC=90°,则F在以AC为直径的圆K上,设点F的坐标,根据KF= AC列方程即可求解.
【解法提示】如解图④⑤,
∵A(-6,0),B(2,0),∴对称轴为直线x=-2,
设点F的坐标为(-2,m)
∵∠FAC+∠FCA=90°,
∴∠AFC=90°.
∴F在以AC为直径的圆上.
∵A(-6,0),C(0,-3),
∴圆心K的坐标为(-3, ).
例2题解图④
例2题解图⑤
(5)存在.点F的坐标为(-2, )或(-2, );
∵KF= AC,KF2=(-2+3)2+(m+ )2,
AC2=62+32=45,
∴(-2+3)2+(m+ )2= ×45,
解得m1= ,m2= ,
∴点F的坐标为(-2, )或(-2, ).
例2题解图④
例2题解图⑤
(6)如图⑥,若点Q在y轴上,点G为该抛物线的顶点,且∠GQA=45°.请直接写出点Q的坐标.
例2题图⑥
【思维教练】要求点Q的坐标,已知点Q在y轴上,点G为该抛物线的顶点,且∠GQA=45°,可得点Q为以AG为弦,AG所对圆心角是90度的圆与y轴的交点,设圆心为R,过点R作x轴的垂线交x轴于点M,交过点G与x轴的平行线于点N,证明△AMR≌△RNG(AAS),直接写出点R坐标,利用圆的性质即可求解.
【解法提示】设△GAQ的外接圆圆心为R,如解图⑥,
∵∠GQA=45°,
∴∠ARG=2∠GQA=90°,
过点R作x轴的垂线交x轴于点M,
交过点G与x轴的平行线于点N,连接GN,
设点R(x,y),G(-2,-4)
则AM=x+6,RM=-y,RN=y+4,GN=x+2,
例2题解图⑥
∵∠MRA+∠GRN=90°,∠GRN+∠RGN=90°,
∴∠RGN=∠ARM,
又∵∠AMR=∠RNG=90°,RA=RG,
∴△AMR≌△RNG,
∴AM=RN,MR=GN,
例2题解图⑥
∴点R(-2,0),
则RA=-2-(-6)=4,
设点Q(0,m),则RQ=RA=4,
即m2+4=16,解得m=±2 ,
∴Q的坐标为(0,2 )或(0,-2 ).
(6)Q的坐标为(0,2 )或(0,-2 ).
例2题解图⑥
综合提升
三阶
1. 如图,二次函数y=- x2+bx+c的图象交x轴于A(-3,0), B(4,0)两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.
第1题图
解:(1)将A(-3,0),B(4,0)代入二次函数表达式 y=- x2+bx+c中,
∴二次函数的表达式为y=- x2+ x+4;
(1)求该二次函数的表达式;
第1题图
(2)∵点A(-3,0),C(0,4),
∴OA=3,OC=4.
∵表达式为y= x2+ +4;
当x=0时,y=4
∴C(0,4),∴OC=4.
∴S△AOC= OA·OC= ×3×4=6,
∵B(4,0),∴BO=4,
(2)当点P在直线BC下方时,连接OP,若S△BOP=2S△AOC,求点P的坐标;
第1题图
P1
P2
m
∵B(4,0),∴BO=4,
设点P到x轴的距离为h,
∵S△BOP=2S△AOC,∴ ×4·h=2×6,解得h=6,
∵点P在直线BC的下方,
∴如解图①,作直线OB的平行线m,
使直线m到直线OB的距离h等于6,
与抛物线的交点即为所求的点P.即y=-6,
则y=- x2+ x+4=-6,解得x1=-5,x2=6,
∴点P的坐标为(-5,-6)或(6,-6);
第1题图
P1
P2
m
(3)在抛物线的对称轴上是否存在一点Q,使得∠AQC=∠ABC?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)存在,如解图②,∵点B(4,0),C(0,4),A(-3,0),
∴∠ABC=45°,AC=5,
∵∠AQC=∠ABC,
∴点Q是△ABC的外接圆M与抛物线对称轴的交点Q、Q′,
连接AM并延长,交 M于点D,
则∠D=∠ABC=45°,
第1题解图②
∵AD是 M的直径,
∴∠ACD=90°,
∴AD= =5 ,
连接BM,设对称轴交x轴于点E,在Rt△BME中,BE2+ME2=MB2,
由(1)得抛物线的对称轴为直线x= ,
∴OE= ,
∴BE=4- =
∴( )2+ME2=( )2,解得ME= (负值已舍去),
第1题解图②
∴QE=MQ+ME= ,EQ′=MQ′-ME= ,
∴点Q的坐标为( , )或( , ).
第1题解图②
2. 在平面直角坐标系中,抛物线y= x2+bx+c与x轴交于A、B两点,与y轴交于点C,直线BC的解析式为y= x-2.
第2题图
(1)∵点B,C在直线y= x-2上,
当x=0时,y=-2;当y=0时,x=4,
∴点B(4,0),点C(0,-2).
∵点B,C在抛物线y= x2+bx+c上,
∴
∴抛物线的解析式为 y= x2- x-2;
(1)求抛物线的解析式;
第2题图
(2)如图①,点M在线段BC上,设点M的横坐标为t,过点M作y轴的平行线,过点C作x轴的平行线,两条平行线相交于点N,将△MCN沿MC翻折得到△MCN′,当点N′落在线段AB上时,求此时t的值;
第2题图
(2)如解图①,当点N′落在AB上时,设直线NM与x轴交于点Q.
∵点M在线段BC上,且点M的横坐标为t,OC=2,
∴点M的纵坐标为 t-2,CN=t.
∴由折叠的性质得CN′=CN=t,
N′M=NM= t-2-(-2)= t,QM=2- t.
∴ON′= .
易证△ON′C∽△QMN′,
∴ ∴
第2题解图①
(3)如图②,点P在直线BC下方的抛物线上,过点P作PQ⊥BC于点Q,当△CPQ中的某个角恰好为2∠ABC时,请直接写出点P的横坐标.
【解法提示】如解图②,过点P作PR⊥y轴,垂足为R,延长PR交BC的延长线于点G.
当∠QCP=2∠ABC时,∠QCP=2∠BGP,
∴∠CPR=∠G=∠ABC,
∴tan∠CPR=tan∠ABC,
∴ = = .
第2题解图②
设点P(x,x2- x-2),则PR=x,
CR=-2-( x2- x-2)=- x2+ x.
∴ = ,
解得x=0(舍去)或x=2.
∴点P的横坐标为2;
如解图③,当∠CPQ=2∠ABC时,
令 y= x2- x-2=0,解得x=-1或x=4(舍去),
第2题解图③
∴A(-1,0).
设AB的中点为F,连接CF,则AF= ,OF= ,FB= ,
∴tan∠OFC= = ,CF= = .
∴FB=FC,∴∠OFC=2∠ABC,
∴tan∠CPQ=tan∠OFC= .
设QP=3k,CQ=4k,则CP=5k.
∵tan∠QGP=tan∠OBC,
∴ = = ,∴GQ=6k,
第2题解图③
∴由勾股定理,得GP= =3 k,
GC=GQ-CQ=2k.
∵在Rt△GCR中,tan∠CGR= ,
∴GR= k,CR= k,
∴RP=GP-GR=3 k- k= k,
∴
第2题解图③
解得x=0(舍去)或x= ,
∴点P的横坐标为 .
综上所述,点P的横坐标为2或 .
第2题解图③
(3)点P的横坐标为2或 .
3. 如图,抛物线y=ax2+bx+3与x轴交于A,B两点(点A在点B的左侧),且对称轴与抛物线交于点M(-1,4),与x轴交于点C,直线y=kx+d过A、M两点.
第3题图
解:(1)∵抛物线的顶点为M(-1,4),
∴可设抛物线的表达式为y=a(x+1)2+4,
∵当x=0时,y=3,
∴3=a+4,解得a=-1,
∴抛物线的表达式为y=-(x+1)2+4,
即y=-x2-2x+3.
令y=-x2-2x+3=0,解得x1=-3,x2=1,
∴A(-3,0),B(1,0),
(1)求抛物线及直线AM的表达式;
第3题图
将A,M两点坐标代入直线y=kx+d中,
∴直线AM的表达式为y=2x+6;
第3题图
(2)∵∠EFD=∠DHA=90°,∠EDF=∠ADH,
∴∠MAC=∠DEF.
∵MC=4,AC=2,
∴AM=
∴cos∠DEF=cos∠MAC=
(2)如图①,点E是AM上方抛物线上一动点,过点E作EF⊥AM于点F,EH⊥x轴于点H,交AM于点D,设点E的横坐标为m,请用含m的代数式表示出EF的长度,并写出m的取值范围;
第3题图
∵点E的横坐标为m
∴E(m,-m2-2m+3),D(m,2m+6),
∴DE=-m2-2m+3-(2m+6)=-m2-4m-3,
∴EF=DE·cos∠DEF= (-m2-4m-3)=- (m+2)2+ .
∵点E是AM上方抛物线上一点,
∴m的取值范围为-3<m<-1;
第3题图
(3)在(2)的条件下,当EF取最大值时,如图②,在y轴上取一点Q,连接AQ,EQ,当∠AQE最大时,求点Q的坐标.
当 P与y轴相切时,∠AQE最大,连接PA,PE,PQ,则PA=PE=PQ,且PQ⊥y轴,
由(2)得,EF=- (m+2)2+ ,
∵- <0,-3∴当m=-2时,EF取得最大值,
此时点E的坐标为(-2,3),
第3题图
第3题解图
(3)如解图,连接AE,作△AEQ的外接圆 P,
设点P的坐标为(x,y),
则PA2=(x+3)2+y2,PE2=(x+2)2+(y-3)2,PQ2=x2,
解得y=9-2 或y=9+2 (不符合题意,舍去),
∴点Q的坐标为(0,9-2 ).
第3题解图
4. 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+6交x轴于A、B两点,交y轴于点C,且OA=OC=3OB,连接AC,动点P和动点Q同时出发,点P从点C以每秒2个单位长度的速度沿CA运动到点A,点Q从点O出发以每秒1个单位长度的速度沿OC运动到点C,连接PQ,当点P到达点A时,点Q停止运动.
第4题图
(1)求抛物线的表达式;
解:(1)∵抛物线y=ax2+bx+6交y轴于点C,
∴点C(0,6),
∴OC=6,
∵OA=OC=3OB,
∴OA=OC=6,OB=2,
∴A(-6,0),B(2,0),
第4题图
∴抛物线的表达式为y=- x2-2x+6;
第4题图
将点A、B的坐标代入y=ax2+bx+6中得,
(2)求S△CPQ的最大值及此时点P的坐标;
(2)由A(6,0),C(0,6)得直线AC的表达式为y=x+6,
∵OA=OC,则∠ACO=45°,
设点P的运动时间为t,由题意得PC=2t,CQ=6-t,
则|xP|=PC·sin45°= t,
则S△CPQ= CQ·|xP|= ×(6-t)× t
=- t2+3 t=- (t-3)2+ ,
第4题图
当t=3时,|xp|=3 ,
∵点P在第二象限,
∴xp=-3 ,
∴yP=6-3 ,
故S△CPQ的最大值为 ,
此时点P的坐标为(-3 ,6-3 );
∵- <0,
∴当t=3时,S△CPQ有最大值,其最大值为 ,
第4题图
(3)点M是抛物线上一点,是否存在点M,使得∠ACM=15°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)存在.
分两种情况讨论:
①如解图①,当点M在AC上方时,
过点M作ME⊥x轴于点E,MF⊥y轴于点F,
∵OC=OA,
∴∠ACO=45°,
∵∠ACM=15°,
∴∠OCM=60°,
第4题解图①
第4题图
设点M(m,- m2-2m+6)(-6<m<0),
在Rt△MCF中,∵CF= ,
∴CF= MF=- m,
∴OF=OC-CF=6+ m,
∵∠MEO=∠EOF=∠MFO=90°,
∴四边形MEOF是矩形,
∴ME=OF,
即- m2-2m+6=6+ m,
解得m1=0(舍去),m2=-4- .
第4题解图①
∴ME=6+ m= ,
∴点M的坐标为(-4- , );
②如解图②,当点M在AC下方时,过点M作MH⊥x轴于点H,设MC与x轴交于点G,
设点M(n,- n2-2n+6)(n<-6),
则OH=-n,MH= n2+2n-6,
∵∠CAO=45°,∠ACM=15°,
∴∠AGM=∠CGO=∠CAO+∠ACM=60°,
在Rt△CGO中,∵OC=6,
第4题解图②
∴OG= =2 ,
∴GH=OH-OG=-n-2 ,
在Rt△MGH中,∵HM=GH·tan∠HGM= GH,
∴- n-6= n2+2n-6,
解得n1=0(舍去),n2=-4-2 .
∴GH=OH-OG=4 ,MH=GH=4 .
∴点M的坐标为(-4-2 ,-4 ).
综上所述,存在点M,使得∠ACM=15°,此时点M的坐标为 (-4- , )或(-4-2 ,-4 ).
第4题解图②
由①知△AOC∽△AQ1B,
∴ ,
∴AO=2,∴AC= ,
在Rt△AQ1B中,AQ1=AO+OQ1=2+4=6,BQ1=3,
∴由勾股定理得AB=
∴
解得m= .
综上所述,若△ABQ与△AOC相似,m的值为4或 ;
第4题解图②
微技能——角的表示
一阶
例 1
一题多设问
已知抛物线交x轴于A、B两
点(点A在点B的左侧),与y轴交于点C,连接AC.
微专题 二次函数与角度问题
例1题图①
【作图依据】_______________________________________________
(1)点P是抛物线上一点,在图①中找出点P使得∠PCA=30°;
例1题图①
解:(1)满足条件的点P如解图①.
分两种情况:
①点P在直线AC上方;
②点P在直线AC下方;
全等三角形对应角相等
例1题解图①
(2)点P是抛物线上一点,在图②中找出点P使得∠CPA=60°;
例1题图②
【作图依据】_____________________________________________
(2)满足条件的点P如解图②.
分两种情况:
①点P在直线AC上方;
②点P在直线AC下方;
例1题解图②
全等三角形对应角相等
(3)点满足条件的点P如解图③.
分两种情况:
①点P在直线AB上方;
②点P在直线AB下方.
【作图依据】_________________________________
(3)点D为抛物线对称轴与x轴的交点,点P是抛物线上一点,在图③中找出点P使得∠PAB=∠DCO.
例1题图③
例1题解图③
全等三角形对应角相等
一题多设问
二阶
例 2
一题多设问
已知抛物线y=ax2+bx+c与x轴交于点A,B ,与y轴交于点C,其中A(-6,0),B(2,0),C(0,-3).
例2题图①
(1)如图①,求抛物线的解析式;
解:(1)将点A、B、C的坐标代入抛物线解析式得,
解得
∴抛物线的解析式为y= x2+x-3;
例2题图①
(2)如图②,在抛物线上是否存在一点P,使得AB为∠PAC的平分线?若存在,请直接写出点P的坐标;若不存在,请说明理由;
例2题图②
【思维教练】要求以AB为∠PAC的平分线的点P的坐标,根据角平分线的性质,作点C关于x轴的对称点C′,先求出直线AC′的解析式,再与抛物线解析式联立,即可得到点P的坐标.
【解法提示】∵点C的坐标为(0,-3),
∴点C关于x轴的对称点C′的坐标为(0,3).
如解图①,连接AC′并延长至与抛物线相交,交点为P,
设直线AC′的解析式为y=kx+b,将A(-6,0),C′(0,3)代入,
得 解得
∴直线AC′的解析式为y= x+3.
例2题解图①
联立
解得
∴点P的坐标为(4,5).
(2)存在,点P的坐标为(4,5);
例2题解图①
(3)如图③,连接AC,AC上存在一点M,使得∠BMC=2∠BAC,请直接写出点M的坐标;
【思维教练】要求点M的坐标,已知∠BMC=2∠BAC,可得∠ABM=∠BAC,即点M在AB的垂直平分线上,可得点M的横坐标,代入AC所在直线解析式,即可求解.
例2题图③
【解法提示】如解图②,过点M作x轴的垂线,垂足为N,连接AC,BM.
∵∠BMC=2∠BAC,∠BMC=∠BAC+∠ABM,
∴∠ABM=∠BAC,
∴AM=BM.
∵MN⊥AB,
∴AN=BN,
∴点M的横坐标为 =-2.
例2题解图②
设直线AC的解析式为y=kx+b(k≠0),将A(-6,0),C(0,-3)代入,
∴直线AC的解析式为y=- x-3.
将x=-2代入y=- x-3中得,y=-2,
∴点M的坐标为(-2,-2).
例2题解图③
(3)点M的坐标为(-2,-2);
(4)如图④,在抛物线上是否存在一点E,使得∠EBA=∠OCA?若存在,请直接写出点E的坐标;若不存在,请说明理由;
例2题图④
【思维教练】要求点E的坐标,已知∠EBA=∠OCA,过点E作EH⊥x轴于点H,则△HBE∽△OCA,设点E的坐标,代入比例关系可列方程求解.
【解法提示】设点E的坐标为(t, t2+t-3),如解图③,过点E作EH⊥x轴于点H,连接EB,AC,
∴H(t,0).
∵∠EBA=∠OCA,∠EHB=∠AOC=90°,
∴△HBE∽△OCA,
例2题解图③
E
H
解得 t1=2,t2=-14,
当t=2时, t2+t-3=0,不符合题意,舍去,
当t=-14时,t2+t-3=32,
∴E(-14,32).
(4)存在,点E的坐标为(-14,32);
例2题解图③
E
H
(5)如图⑤,在抛物线的对称轴上是否存在点F,使得∠FAC+∠FCA=90°?若存在,直接写出点F的坐标;如不存在,请说明理由;
例2题图⑤
【思维教练】要求点F的坐标,已知∠FAC+∠FCA=90°可得∠AFC=90°,则F在以AC为直径的圆K上,设点F的坐标,根据KF= AC列方程即可求解.
【解法提示】如解图④⑤,
∵A(-6,0),B(2,0),∴对称轴为直线x=-2,
设点F的坐标为(-2,m)
∵∠FAC+∠FCA=90°,
∴∠AFC=90°.
∴F在以AC为直径的圆上.
∵A(-6,0),C(0,-3),
∴圆心K的坐标为(-3, ).
例2题解图④
例2题解图⑤
(5)存在.点F的坐标为(-2, )或(-2, );
∵KF= AC,KF2=(-2+3)2+(m+ )2,
AC2=62+32=45,
∴(-2+3)2+(m+ )2= ×45,
解得m1= ,m2= ,
∴点F的坐标为(-2, )或(-2, ).
例2题解图④
例2题解图⑤
(6)如图⑥,若点Q在y轴上,点G为该抛物线的顶点,且∠GQA=45°.请直接写出点Q的坐标.
例2题图⑥
【思维教练】要求点Q的坐标,已知点Q在y轴上,点G为该抛物线的顶点,且∠GQA=45°,可得点Q为以AG为弦,AG所对圆心角是90度的圆与y轴的交点,设圆心为R,过点R作x轴的垂线交x轴于点M,交过点G与x轴的平行线于点N,证明△AMR≌△RNG(AAS),直接写出点R坐标,利用圆的性质即可求解.
【解法提示】设△GAQ的外接圆圆心为R,如解图⑥,
∵∠GQA=45°,
∴∠ARG=2∠GQA=90°,
过点R作x轴的垂线交x轴于点M,
交过点G与x轴的平行线于点N,连接GN,
设点R(x,y),G(-2,-4)
则AM=x+6,RM=-y,RN=y+4,GN=x+2,
例2题解图⑥
∵∠MRA+∠GRN=90°,∠GRN+∠RGN=90°,
∴∠RGN=∠ARM,
又∵∠AMR=∠RNG=90°,RA=RG,
∴△AMR≌△RNG,
∴AM=RN,MR=GN,
例2题解图⑥
∴点R(-2,0),
则RA=-2-(-6)=4,
设点Q(0,m),则RQ=RA=4,
即m2+4=16,解得m=±2 ,
∴Q的坐标为(0,2 )或(0,-2 ).
(6)Q的坐标为(0,2 )或(0,-2 ).
例2题解图⑥
综合提升
三阶
1. 如图,二次函数y=- x2+bx+c的图象交x轴于A(-3,0), B(4,0)两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.
第1题图
解:(1)将A(-3,0),B(4,0)代入二次函数表达式 y=- x2+bx+c中,
∴二次函数的表达式为y=- x2+ x+4;
(1)求该二次函数的表达式;
第1题图
(2)∵点A(-3,0),C(0,4),
∴OA=3,OC=4.
∵表达式为y= x2+ +4;
当x=0时,y=4
∴C(0,4),∴OC=4.
∴S△AOC= OA·OC= ×3×4=6,
∵B(4,0),∴BO=4,
(2)当点P在直线BC下方时,连接OP,若S△BOP=2S△AOC,求点P的坐标;
第1题图
P1
P2
m
∵B(4,0),∴BO=4,
设点P到x轴的距离为h,
∵S△BOP=2S△AOC,∴ ×4·h=2×6,解得h=6,
∵点P在直线BC的下方,
∴如解图①,作直线OB的平行线m,
使直线m到直线OB的距离h等于6,
与抛物线的交点即为所求的点P.即y=-6,
则y=- x2+ x+4=-6,解得x1=-5,x2=6,
∴点P的坐标为(-5,-6)或(6,-6);
第1题图
P1
P2
m
(3)在抛物线的对称轴上是否存在一点Q,使得∠AQC=∠ABC?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)存在,如解图②,∵点B(4,0),C(0,4),A(-3,0),
∴∠ABC=45°,AC=5,
∵∠AQC=∠ABC,
∴点Q是△ABC的外接圆M与抛物线对称轴的交点Q、Q′,
连接AM并延长,交 M于点D,
则∠D=∠ABC=45°,
第1题解图②
∵AD是 M的直径,
∴∠ACD=90°,
∴AD= =5 ,
连接BM,设对称轴交x轴于点E,在Rt△BME中,BE2+ME2=MB2,
由(1)得抛物线的对称轴为直线x= ,
∴OE= ,
∴BE=4- =
∴( )2+ME2=( )2,解得ME= (负值已舍去),
第1题解图②
∴QE=MQ+ME= ,EQ′=MQ′-ME= ,
∴点Q的坐标为( , )或( , ).
第1题解图②
2. 在平面直角坐标系中,抛物线y= x2+bx+c与x轴交于A、B两点,与y轴交于点C,直线BC的解析式为y= x-2.
第2题图
(1)∵点B,C在直线y= x-2上,
当x=0时,y=-2;当y=0时,x=4,
∴点B(4,0),点C(0,-2).
∵点B,C在抛物线y= x2+bx+c上,
∴
∴抛物线的解析式为 y= x2- x-2;
(1)求抛物线的解析式;
第2题图
(2)如图①,点M在线段BC上,设点M的横坐标为t,过点M作y轴的平行线,过点C作x轴的平行线,两条平行线相交于点N,将△MCN沿MC翻折得到△MCN′,当点N′落在线段AB上时,求此时t的值;
第2题图
(2)如解图①,当点N′落在AB上时,设直线NM与x轴交于点Q.
∵点M在线段BC上,且点M的横坐标为t,OC=2,
∴点M的纵坐标为 t-2,CN=t.
∴由折叠的性质得CN′=CN=t,
N′M=NM= t-2-(-2)= t,QM=2- t.
∴ON′= .
易证△ON′C∽△QMN′,
∴ ∴
第2题解图①
(3)如图②,点P在直线BC下方的抛物线上,过点P作PQ⊥BC于点Q,当△CPQ中的某个角恰好为2∠ABC时,请直接写出点P的横坐标.
【解法提示】如解图②,过点P作PR⊥y轴,垂足为R,延长PR交BC的延长线于点G.
当∠QCP=2∠ABC时,∠QCP=2∠BGP,
∴∠CPR=∠G=∠ABC,
∴tan∠CPR=tan∠ABC,
∴ = = .
第2题解图②
设点P(x,x2- x-2),则PR=x,
CR=-2-( x2- x-2)=- x2+ x.
∴ = ,
解得x=0(舍去)或x=2.
∴点P的横坐标为2;
如解图③,当∠CPQ=2∠ABC时,
令 y= x2- x-2=0,解得x=-1或x=4(舍去),
第2题解图③
∴A(-1,0).
设AB的中点为F,连接CF,则AF= ,OF= ,FB= ,
∴tan∠OFC= = ,CF= = .
∴FB=FC,∴∠OFC=2∠ABC,
∴tan∠CPQ=tan∠OFC= .
设QP=3k,CQ=4k,则CP=5k.
∵tan∠QGP=tan∠OBC,
∴ = = ,∴GQ=6k,
第2题解图③
∴由勾股定理,得GP= =3 k,
GC=GQ-CQ=2k.
∵在Rt△GCR中,tan∠CGR= ,
∴GR= k,CR= k,
∴RP=GP-GR=3 k- k= k,
∴
第2题解图③
解得x=0(舍去)或x= ,
∴点P的横坐标为 .
综上所述,点P的横坐标为2或 .
第2题解图③
(3)点P的横坐标为2或 .
3. 如图,抛物线y=ax2+bx+3与x轴交于A,B两点(点A在点B的左侧),且对称轴与抛物线交于点M(-1,4),与x轴交于点C,直线y=kx+d过A、M两点.
第3题图
解:(1)∵抛物线的顶点为M(-1,4),
∴可设抛物线的表达式为y=a(x+1)2+4,
∵当x=0时,y=3,
∴3=a+4,解得a=-1,
∴抛物线的表达式为y=-(x+1)2+4,
即y=-x2-2x+3.
令y=-x2-2x+3=0,解得x1=-3,x2=1,
∴A(-3,0),B(1,0),
(1)求抛物线及直线AM的表达式;
第3题图
将A,M两点坐标代入直线y=kx+d中,
∴直线AM的表达式为y=2x+6;
第3题图
(2)∵∠EFD=∠DHA=90°,∠EDF=∠ADH,
∴∠MAC=∠DEF.
∵MC=4,AC=2,
∴AM=
∴cos∠DEF=cos∠MAC=
(2)如图①,点E是AM上方抛物线上一动点,过点E作EF⊥AM于点F,EH⊥x轴于点H,交AM于点D,设点E的横坐标为m,请用含m的代数式表示出EF的长度,并写出m的取值范围;
第3题图
∵点E的横坐标为m
∴E(m,-m2-2m+3),D(m,2m+6),
∴DE=-m2-2m+3-(2m+6)=-m2-4m-3,
∴EF=DE·cos∠DEF= (-m2-4m-3)=- (m+2)2+ .
∵点E是AM上方抛物线上一点,
∴m的取值范围为-3<m<-1;
第3题图
(3)在(2)的条件下,当EF取最大值时,如图②,在y轴上取一点Q,连接AQ,EQ,当∠AQE最大时,求点Q的坐标.
当 P与y轴相切时,∠AQE最大,连接PA,PE,PQ,则PA=PE=PQ,且PQ⊥y轴,
由(2)得,EF=- (m+2)2+ ,
∵- <0,-3
此时点E的坐标为(-2,3),
第3题图
第3题解图
(3)如解图,连接AE,作△AEQ的外接圆 P,
设点P的坐标为(x,y),
则PA2=(x+3)2+y2,PE2=(x+2)2+(y-3)2,PQ2=x2,
解得y=9-2 或y=9+2 (不符合题意,舍去),
∴点Q的坐标为(0,9-2 ).
第3题解图
4. 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+6交x轴于A、B两点,交y轴于点C,且OA=OC=3OB,连接AC,动点P和动点Q同时出发,点P从点C以每秒2个单位长度的速度沿CA运动到点A,点Q从点O出发以每秒1个单位长度的速度沿OC运动到点C,连接PQ,当点P到达点A时,点Q停止运动.
第4题图
(1)求抛物线的表达式;
解:(1)∵抛物线y=ax2+bx+6交y轴于点C,
∴点C(0,6),
∴OC=6,
∵OA=OC=3OB,
∴OA=OC=6,OB=2,
∴A(-6,0),B(2,0),
第4题图
∴抛物线的表达式为y=- x2-2x+6;
第4题图
将点A、B的坐标代入y=ax2+bx+6中得,
(2)求S△CPQ的最大值及此时点P的坐标;
(2)由A(6,0),C(0,6)得直线AC的表达式为y=x+6,
∵OA=OC,则∠ACO=45°,
设点P的运动时间为t,由题意得PC=2t,CQ=6-t,
则|xP|=PC·sin45°= t,
则S△CPQ= CQ·|xP|= ×(6-t)× t
=- t2+3 t=- (t-3)2+ ,
第4题图
当t=3时,|xp|=3 ,
∵点P在第二象限,
∴xp=-3 ,
∴yP=6-3 ,
故S△CPQ的最大值为 ,
此时点P的坐标为(-3 ,6-3 );
∵- <0,
∴当t=3时,S△CPQ有最大值,其最大值为 ,
第4题图
(3)点M是抛物线上一点,是否存在点M,使得∠ACM=15°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)存在.
分两种情况讨论:
①如解图①,当点M在AC上方时,
过点M作ME⊥x轴于点E,MF⊥y轴于点F,
∵OC=OA,
∴∠ACO=45°,
∵∠ACM=15°,
∴∠OCM=60°,
第4题解图①
第4题图
设点M(m,- m2-2m+6)(-6<m<0),
在Rt△MCF中,∵CF= ,
∴CF= MF=- m,
∴OF=OC-CF=6+ m,
∵∠MEO=∠EOF=∠MFO=90°,
∴四边形MEOF是矩形,
∴ME=OF,
即- m2-2m+6=6+ m,
解得m1=0(舍去),m2=-4- .
第4题解图①
∴ME=6+ m= ,
∴点M的坐标为(-4- , );
②如解图②,当点M在AC下方时,过点M作MH⊥x轴于点H,设MC与x轴交于点G,
设点M(n,- n2-2n+6)(n<-6),
则OH=-n,MH= n2+2n-6,
∵∠CAO=45°,∠ACM=15°,
∴∠AGM=∠CGO=∠CAO+∠ACM=60°,
在Rt△CGO中,∵OC=6,
第4题解图②
∴OG= =2 ,
∴GH=OH-OG=-n-2 ,
在Rt△MGH中,∵HM=GH·tan∠HGM= GH,
∴- n-6= n2+2n-6,
解得n1=0(舍去),n2=-4-2 .
∴GH=OH-OG=4 ,MH=GH=4 .
∴点M的坐标为(-4-2 ,-4 ).
综上所述,存在点M,使得∠ACM=15°,此时点M的坐标为 (-4- , )或(-4-2 ,-4 ).
第4题解图②
由①知△AOC∽△AQ1B,
∴ ,
∴AO=2,∴AC= ,
在Rt△AQ1B中,AQ1=AO+OQ1=2+4=6,BQ1=3,
∴由勾股定理得AB=
∴
解得m= .
综上所述,若△ABQ与△AOC相似,m的值为4或 ;
第4题解图②
同课章节目录
