2024辽宁中考数学三轮冲刺系列 全国视野创新题型推荐(课件)50张PPT
文档属性
| 名称 | 2024辽宁中考数学三轮冲刺系列 全国视野创新题型推荐(课件)50张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 603.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 21:21:33 | ||
图片预览











文档简介
(共50张PPT)
题型一 跨学科试题
【全国视野解读】《教育部关于加强初中学业水平考试命题工作的意见》中指出“积极探索跨学科命题”.该命题模式让学生体会数学与其他学科之间的联系.通过学科知识间的融合,提升学生运用所学知识解决复杂问题的能力,故推荐此题型高效备考.目前各地中考命题都在陆续融入跨学科试题.
1.[跨生物学科]———遗传基因
根据生物学家的研究,人体的许多特征都是由基因控制的.有的人是单眼皮,有的人是双眼皮,这是由一对人体基因控制的.控制单眼皮的基因f是隐性的,控制双眼皮的基因F是显性的,控制眼皮的一对基因可能是ff,FF,Ff.其中基因ff的人是单眼皮,基因FF,Ff的人是双眼皮,父母分别将他们的一对基因中的一个遗传给子女,而且是等可能的.
(1)如果父母都是双眼皮且他们的基因都是Ff,则他们的子女是单眼皮的概率为______;
(2)如果母亲是双眼皮且基因是FF,父亲是单眼皮,他们的子女是双眼皮还是单眼皮?为什么?
(2)子女是双眼皮.
因为子女从母亲的基因中遗传得到基因F,从父亲的基因中遗传得到基因f,故子女的基因只有一种可能Ff,为双眼皮.
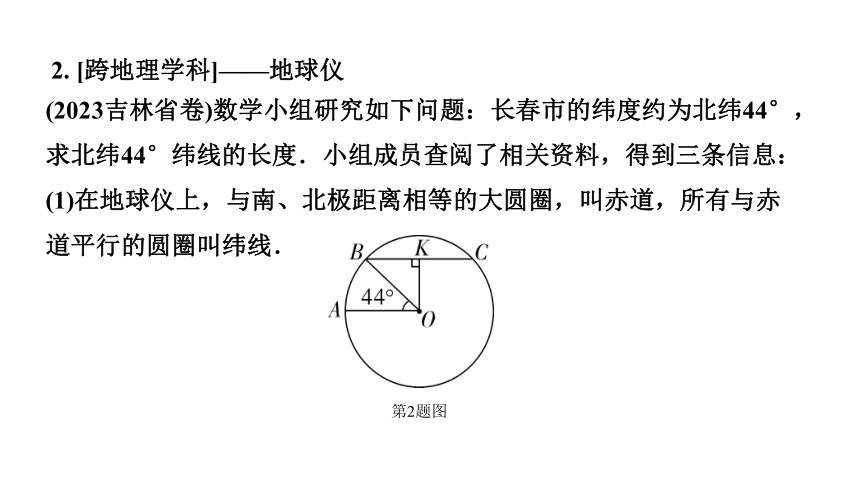
2. [跨地理学科]——地球仪
(2023吉林省卷)数学小组研究如下问题:长春市的纬度约为北纬44°,求北纬44°纬线的长度.小组成员查阅了相关资料,得到三条信息:
(1)在地球仪上,与南、北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线.
第2题图
(2)如图, O是经过南、北极的圆,地球半径OA约为6400 km,弦BC∥OA,过点O作OK⊥BC于点K.连接OB.若∠AOB=44°,则以BK为半径的圆的周长是北纬44°纬线的长度.
(3)参考数据:π取3,sin44°≈0.69,cos44°≈0.72.
小组成员给出了如下解答,请你补充完整:
解:两直线平行,内错角相等,
cosB,0.72,27648
3. [跨物理学科]——欧姆定律
(2023台州)电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R1, R1与踏板上人的质量m之间的函数关系式为R1=km+b(其中k,b为常数,0≤m≤120),其图象如图①所示;图②的电路中,电源电压恒为8伏,定值电阻R0的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为U0 ,该读数可以换算为人的质量m,
第3题图
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I= ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.
(1)求k,b的值;
解:(1)因为图象经过点(120,0)与点(0,240),代入R1=km+b,
(2)求R1关于U0的函数解析式;
(2)由题意,得 .
化简,得R1= -30;
(3)用含U0的代数式表示m;
(3)由(1)得:R1=-2m+240(0≤m≤120).
将R1=-2m+240代人R1= -30.化简,得m=- +135(0≤m≤120);
(4)若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.
(4)当U0>0时, 随U0的增大而增大,∴m随U0的增大而增大.
当U0=6时,m有最大值,m最大=-20+135=115.
∴该电子称最大可称质量为115千克.
题型三 统计题——数据的收集与整理
【全国视野解读】此题型是对教改文件中要求的注重学生过程体验的落实,通过数据的收集、整理与分析,培养学生运用所学统计知识解决现实生活问题的能力.故推荐此题型高效备考.
1. (2023广西北部湾经济区)某水果公司以10元/kg的成本价新进2000箱荔枝,每箱质量5 kg,在出售荔枝前,需要去掉损坏的荔枝,现随机抽取20箱,去掉损坏荔枝后称得每箱的质量(单位:kg)如下:
4.7 4.8 4.6 4.5 4.8 4.9 4.8 4.7 4.8 4.7
4.8 4.9 4.7 4.8 4.5 4.7 4.7 4.9 4.7 5.0
整理数据:
质量(kg) 4.5 4.6 4.7 4.8 4.9 5.0
数量(箱) 2 1 7 a 3 1
分析数据:
平均数 众数 中位数
4.75 b c
(1)直接写出上述表格中a,b,c的值.
【解法提示】由数据可知a=6;数据中出现次数最多的是4.7,所以众数为4.7;将数据从小到大排列,第10、11位数为4.7和4.8,所以中位数为 =4.75.
解:(1)a=6,b=4.7,c=4.75;
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这2000箱荔枝共损坏了多少千克?
(2)选平均数4.75 kg,所以2000箱荔枝共损坏2000×(5-4.75)=500 kg;
(3)根据(2)中的结果,求该公司销售这批荔枝每千克定为多少元才不亏本(结果保留一位小数)
(3)根据题意得 ≈10.52
∴Y应取10.6(元/千克),
答:该公司销售这批荔枝每千克定为10.6元才不亏本.
2. (2023北京)为了解甲、乙两座城市的邮政企业4月份收入的情况,从这两座城市的邮政企业中,各随机抽取了25家邮政企业,获得了它们4月份收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.甲城市邮政企业4月份收入的数据的频数分布直方图如下(数据分成5组:6≤x<8,8≤x<10,10≤x<12,
12≤x<14,14≤x≤16):
第2题图
b.甲城市邮政企业4月份收入的数据在10≤x<12这一组的是:
10.0 10.0 10.1 10.9 11.4 11.5 11.6 11.8
c.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下:
平均数 中位数
甲城市 10.8 m
乙城市 11.0 11.5
根据以上信息,回答下列问题:
(1)写出表中m的值;
【解法提示】甲城市的中位数为将25个数据从小到大排列后,第13个数据,为10.1,
∴m=10.1.
(1)m=10.1;
(2)在甲城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为p1.在乙城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为p2.比较p1,p2的大小,并说明理由;
(2)p1∵甲城市抽取的邮政企业的4月份收入的平均数为10.8,
∴p1=5+3+4=12.
∵乙城市抽取的邮政企业的4月份收入的平均数为11.0,中位数为11.5,11.0<11.5,∴p2≥13,∴p1(3)若乙城市共有200家邮政企业,估计乙城市的邮政企业4月份的总收入(直接写出结果).
【解法提示】乙城市的邮政企业4月份的总收入约为200×11.0=2200(百万元).
(3)2200百万元.
题型四 阅读理解题
【全国视野解读】近年中考命题越来越重视对阅读能力的考查,从阅读活动中发挥学生的主体作用,加深对教学语言、知识、技能、思想、方法的理解,对发展学生核心素养起到极大的作用,故推荐此题型高效备考.
1. (2023山西)阅读与思考
请阅读下列科普材料,并完成相应的任务.
任务:
(1)请根据以上材料简要说明图算法的优越性;
(2)请用以下两种方法验证第二个例子中图算法的正确性.
①用公式 计算:当R1=7.5,R2=5时,R的值为多少;
解:(1)答案不唯一,如:图算法方便,直观;或不用公式计算即可得出结果等;
(2)①当R1=7.5,R2=5,时, .
∴R=3;
②如图,在△AOB中,∠AOB=120°,OC是△AOB的角平分线,OA=7.5,OB=5,用你所学的几何知识求线段OC的长
第1题图
②依题意,画出△AOB,∠AOB=120°,OC平分∠AOB,AO=7.5,BO=5,如解图,过点A作AM∥CO,交BO的延长线于点M.
∵OC平分∠AOB,
∴∠1=∠2= ∠AOB= ×120°=60°.
∵AM∥CO,
∴∠3=∠2=60°,∠M=∠1=60°,
∴∠3=∠M=60°,∴OA=OM,
∴△OAM为等边三角形,
∴OM=MA=OA=7.5.
第1题解图
M
3
2
1
∵∠B=∠B,∠1=∠M,
∴△BCO∽△BAM.
∴ .
∴ .
∴OC=3.
第1题解图
M
3
2
1
2. (2023北京)在平面直角坐标系xOy中, O的半径为1.对于点A和线段BC,给出如下定义:
若将线段BC绕点A旋转可以得到 O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是 O的以点A为中心的“关联线段”.
(1)如图,点A,B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中, O的以点A为中心的“关联线段”是________;
B2C2
第2题图
(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A为中心的“关联线段”,求t的值;
(2)设以点A为圆心,1为半径的圆与⊙O交于点B′,C′,连接B′C′,
第2题解图②
第2题解图②
由题意得,B′C′=1,且点B′与点C′关于y轴对称,
当t>0时,如解图②,
则AB′=AC′=OB′=OC′=B′C′=1,
∴四边形AB′OC′是菱形,△OB′C′是等边三角形,
∴∠B′OC′=60°,
∴∠AB′O=120°,
∴OA= OB′= ,
∴t= ;
当t<0时,如解图③,同理可得,OA= OB′= ,
∴t=- ;
综上所述,t的值为 或- ;
第2题解图③
(3)在△ABC中,AB=1,AC=2.若BC是 O的以点A为中心的“关联线段”,直接写出OA的最小值和最大值,以及相应的BC长.
【解法提示】∵AB=1,AC=2,BC是⊙O的以点A为中心的“关联线段”,
∴以点A为圆心,分别以AB、AC长为半径的圆与⊙O必定有交点,∴OA的最小值为1,OA的最大值为2.当OA最小时,即点A在⊙O上,
如解图④,AB′=AB=1,AC′=AC=2,此时AC′为⊙O的直径,∴∠AB′C′=90°,
∴BC=B′C′= ;
第2题解图④
当OA最大时,如解图⑤,AB′=AB=1,AC′=AC=2,过点A作AM⊥OC′于点M,过点C′作C′N⊥OA于点N,
∵AC′=AO=2,∴OM= OC′= ,
∴AM= = .
∵S△AOC′= OA·C′N= OC′·AM,
∴C′N= = ,
∴ON= = ,
第2题解图⑤
∴B′N=OB′-ON= ,
∴B′C′= = .
(3)OA的最小值为1,此时BC的长为 ;OA的最大值为2,此时BC的长为 .
第2题解图⑤
题型五 中考新考法试题
【全国视野解读】此题型是对教改文件中提及的改变相对固化的试题形式的落实,通过改变试题形式,同时增加开放性试题,开阔学生思维,拓宽学生眼界.故推荐此题型高效备考.
类型一 结构不良试题
【条件开放】——任选条件进行解答
1. (2023宿迁)在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知:如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上,___________________(填写序号).
求证:BE=DF.
注:如果选择多个条件分别解答,按第一个解答计分.
选②(答案不唯一)
第1题图
第1题图
解:选②(答案不唯一);
证明:∵四边形ABCD是平行四边形,
∴OD=OB,
在△BEO和△DFO中,
∴△BEO △DFO,
∴BE=DF.
≌
【结论开放】——结论不固定,合理即可
2. (2023贵阳)有三个不等式2x+3<-1,-5x>15,3(x-1)>6,请在其中任选两个不等式,组成一个不等式组,并求出它的解集.
解:
∴原不等式组解集为x<-3.(答案不唯一)
3. (2023潍坊)甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为________________________.
y=-2x+1(答案不唯一)
类型二 填空双空题
1. (2023北京)某企业有A,B两条加工相同原材料的生产线.在一天内,A生产线共加工a吨原材料,加工时间为(4a+1)小时;在一天内,B生产线共加工b吨原材料,加工时间为(2b+3)小时.第一天,该企业将5吨原材料分配到A,B两条生产线,两条生产线都在一天内完成了加工,且加工时间相同,则分配到A生产线的吨数与分配到B生产线的吨数的
比为______.
第二天开工前,该企业按第一天的分配结果分配了5吨原材料后,又给A生产线分配了m吨原材料,给B生产线分配了n吨原材料.若两条生产线都能在一天内加工完各自分配到的所有原材料,且加工时间相
同,则 的值为______.
2. (2023嘉兴)如图,在△ABC中,∠BAC=30°, ∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动.连接CP,点A关于直线CP的对称点为A′,连接A′C,A′P.在运动过程中,点A′到直线AB距离的最大值是____________;点P到达点B时,线段
A′P扫过的面积为__________________.
第2题图
类型三 补充依据
1. (2023长沙)人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
已知:△ABC.
求作:△A′B′C′,使得△A′B′C′≌△ABC.
作法:如图.
请你根据以上材料完成下列问题:
(1)完成下面证明过程(将正确答案填在相应的横线上):
证明:由作图可知,在△A′B′C′和△ABC中,
(1)画B′C′=BC;
(2)分别以点B′,C′为圆心,线段AB,AC长为半径画弧,两弧相交于点A′;
(3)连接线段A′B′,A′C′,则△A′B′C′即为所求作的三角形.
∴△A′B′C′ ________.
(2)这种作一个三角形与已知三角形全等的方法的依据是________.(填序号)
①AAS ②ASA ③SAS ④SSS
④
≌
△ABC
AB
AC
2. (2022北京)已知:如图,△ABC为锐角三角形,AB=AC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP= ∠BAC.
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作的线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
第2题图
解:(1)补全图形如解图;
第2题解图
(2)完成下面的证明.
证明:∵CD∥AB,
∴∠ABP=________.
∵AB=AC,
∴点B在A上.
又∵点C,P都在 A上,
∴∠BPC= ∠BAC(__________________________________________
_______________________)(填推理的依据).
∴∠ABP= ∠BAC.
∠CPB
在同圆或等圆中,同弧所对的圆周角等于它所
对的圆心角的一半.
题型一 跨学科试题
【全国视野解读】《教育部关于加强初中学业水平考试命题工作的意见》中指出“积极探索跨学科命题”.该命题模式让学生体会数学与其他学科之间的联系.通过学科知识间的融合,提升学生运用所学知识解决复杂问题的能力,故推荐此题型高效备考.目前各地中考命题都在陆续融入跨学科试题.
1.[跨生物学科]———遗传基因
根据生物学家的研究,人体的许多特征都是由基因控制的.有的人是单眼皮,有的人是双眼皮,这是由一对人体基因控制的.控制单眼皮的基因f是隐性的,控制双眼皮的基因F是显性的,控制眼皮的一对基因可能是ff,FF,Ff.其中基因ff的人是单眼皮,基因FF,Ff的人是双眼皮,父母分别将他们的一对基因中的一个遗传给子女,而且是等可能的.
(1)如果父母都是双眼皮且他们的基因都是Ff,则他们的子女是单眼皮的概率为______;
(2)如果母亲是双眼皮且基因是FF,父亲是单眼皮,他们的子女是双眼皮还是单眼皮?为什么?
(2)子女是双眼皮.
因为子女从母亲的基因中遗传得到基因F,从父亲的基因中遗传得到基因f,故子女的基因只有一种可能Ff,为双眼皮.
2. [跨地理学科]——地球仪
(2023吉林省卷)数学小组研究如下问题:长春市的纬度约为北纬44°,求北纬44°纬线的长度.小组成员查阅了相关资料,得到三条信息:
(1)在地球仪上,与南、北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线.
第2题图
(2)如图, O是经过南、北极的圆,地球半径OA约为6400 km,弦BC∥OA,过点O作OK⊥BC于点K.连接OB.若∠AOB=44°,则以BK为半径的圆的周长是北纬44°纬线的长度.
(3)参考数据:π取3,sin44°≈0.69,cos44°≈0.72.
小组成员给出了如下解答,请你补充完整:
解:两直线平行,内错角相等,
cosB,0.72,27648
3. [跨物理学科]——欧姆定律
(2023台州)电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R1, R1与踏板上人的质量m之间的函数关系式为R1=km+b(其中k,b为常数,0≤m≤120),其图象如图①所示;图②的电路中,电源电压恒为8伏,定值电阻R0的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为U0 ,该读数可以换算为人的质量m,
第3题图
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I= ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.
(1)求k,b的值;
解:(1)因为图象经过点(120,0)与点(0,240),代入R1=km+b,
(2)求R1关于U0的函数解析式;
(2)由题意,得 .
化简,得R1= -30;
(3)用含U0的代数式表示m;
(3)由(1)得:R1=-2m+240(0≤m≤120).
将R1=-2m+240代人R1= -30.化简,得m=- +135(0≤m≤120);
(4)若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.
(4)当U0>0时, 随U0的增大而增大,∴m随U0的增大而增大.
当U0=6时,m有最大值,m最大=-20+135=115.
∴该电子称最大可称质量为115千克.
题型三 统计题——数据的收集与整理
【全国视野解读】此题型是对教改文件中要求的注重学生过程体验的落实,通过数据的收集、整理与分析,培养学生运用所学统计知识解决现实生活问题的能力.故推荐此题型高效备考.
1. (2023广西北部湾经济区)某水果公司以10元/kg的成本价新进2000箱荔枝,每箱质量5 kg,在出售荔枝前,需要去掉损坏的荔枝,现随机抽取20箱,去掉损坏荔枝后称得每箱的质量(单位:kg)如下:
4.7 4.8 4.6 4.5 4.8 4.9 4.8 4.7 4.8 4.7
4.8 4.9 4.7 4.8 4.5 4.7 4.7 4.9 4.7 5.0
整理数据:
质量(kg) 4.5 4.6 4.7 4.8 4.9 5.0
数量(箱) 2 1 7 a 3 1
分析数据:
平均数 众数 中位数
4.75 b c
(1)直接写出上述表格中a,b,c的值.
【解法提示】由数据可知a=6;数据中出现次数最多的是4.7,所以众数为4.7;将数据从小到大排列,第10、11位数为4.7和4.8,所以中位数为 =4.75.
解:(1)a=6,b=4.7,c=4.75;
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这2000箱荔枝共损坏了多少千克?
(2)选平均数4.75 kg,所以2000箱荔枝共损坏2000×(5-4.75)=500 kg;
(3)根据(2)中的结果,求该公司销售这批荔枝每千克定为多少元才不亏本(结果保留一位小数)
(3)根据题意得 ≈10.52
∴Y应取10.6(元/千克),
答:该公司销售这批荔枝每千克定为10.6元才不亏本.
2. (2023北京)为了解甲、乙两座城市的邮政企业4月份收入的情况,从这两座城市的邮政企业中,各随机抽取了25家邮政企业,获得了它们4月份收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.甲城市邮政企业4月份收入的数据的频数分布直方图如下(数据分成5组:6≤x<8,8≤x<10,10≤x<12,
12≤x<14,14≤x≤16):
第2题图
b.甲城市邮政企业4月份收入的数据在10≤x<12这一组的是:
10.0 10.0 10.1 10.9 11.4 11.5 11.6 11.8
c.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下:
平均数 中位数
甲城市 10.8 m
乙城市 11.0 11.5
根据以上信息,回答下列问题:
(1)写出表中m的值;
【解法提示】甲城市的中位数为将25个数据从小到大排列后,第13个数据,为10.1,
∴m=10.1.
(1)m=10.1;
(2)在甲城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为p1.在乙城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为p2.比较p1,p2的大小,并说明理由;
(2)p1
∴p1=5+3+4=12.
∵乙城市抽取的邮政企业的4月份收入的平均数为11.0,中位数为11.5,11.0<11.5,∴p2≥13,∴p1
【解法提示】乙城市的邮政企业4月份的总收入约为200×11.0=2200(百万元).
(3)2200百万元.
题型四 阅读理解题
【全国视野解读】近年中考命题越来越重视对阅读能力的考查,从阅读活动中发挥学生的主体作用,加深对教学语言、知识、技能、思想、方法的理解,对发展学生核心素养起到极大的作用,故推荐此题型高效备考.
1. (2023山西)阅读与思考
请阅读下列科普材料,并完成相应的任务.
任务:
(1)请根据以上材料简要说明图算法的优越性;
(2)请用以下两种方法验证第二个例子中图算法的正确性.
①用公式 计算:当R1=7.5,R2=5时,R的值为多少;
解:(1)答案不唯一,如:图算法方便,直观;或不用公式计算即可得出结果等;
(2)①当R1=7.5,R2=5,时, .
∴R=3;
②如图,在△AOB中,∠AOB=120°,OC是△AOB的角平分线,OA=7.5,OB=5,用你所学的几何知识求线段OC的长
第1题图
②依题意,画出△AOB,∠AOB=120°,OC平分∠AOB,AO=7.5,BO=5,如解图,过点A作AM∥CO,交BO的延长线于点M.
∵OC平分∠AOB,
∴∠1=∠2= ∠AOB= ×120°=60°.
∵AM∥CO,
∴∠3=∠2=60°,∠M=∠1=60°,
∴∠3=∠M=60°,∴OA=OM,
∴△OAM为等边三角形,
∴OM=MA=OA=7.5.
第1题解图
M
3
2
1
∵∠B=∠B,∠1=∠M,
∴△BCO∽△BAM.
∴ .
∴ .
∴OC=3.
第1题解图
M
3
2
1
2. (2023北京)在平面直角坐标系xOy中, O的半径为1.对于点A和线段BC,给出如下定义:
若将线段BC绕点A旋转可以得到 O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是 O的以点A为中心的“关联线段”.
(1)如图,点A,B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中, O的以点A为中心的“关联线段”是________;
B2C2
第2题图
(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A为中心的“关联线段”,求t的值;
(2)设以点A为圆心,1为半径的圆与⊙O交于点B′,C′,连接B′C′,
第2题解图②
第2题解图②
由题意得,B′C′=1,且点B′与点C′关于y轴对称,
当t>0时,如解图②,
则AB′=AC′=OB′=OC′=B′C′=1,
∴四边形AB′OC′是菱形,△OB′C′是等边三角形,
∴∠B′OC′=60°,
∴∠AB′O=120°,
∴OA= OB′= ,
∴t= ;
当t<0时,如解图③,同理可得,OA= OB′= ,
∴t=- ;
综上所述,t的值为 或- ;
第2题解图③
(3)在△ABC中,AB=1,AC=2.若BC是 O的以点A为中心的“关联线段”,直接写出OA的最小值和最大值,以及相应的BC长.
【解法提示】∵AB=1,AC=2,BC是⊙O的以点A为中心的“关联线段”,
∴以点A为圆心,分别以AB、AC长为半径的圆与⊙O必定有交点,∴OA的最小值为1,OA的最大值为2.当OA最小时,即点A在⊙O上,
如解图④,AB′=AB=1,AC′=AC=2,此时AC′为⊙O的直径,∴∠AB′C′=90°,
∴BC=B′C′= ;
第2题解图④
当OA最大时,如解图⑤,AB′=AB=1,AC′=AC=2,过点A作AM⊥OC′于点M,过点C′作C′N⊥OA于点N,
∵AC′=AO=2,∴OM= OC′= ,
∴AM= = .
∵S△AOC′= OA·C′N= OC′·AM,
∴C′N= = ,
∴ON= = ,
第2题解图⑤
∴B′N=OB′-ON= ,
∴B′C′= = .
(3)OA的最小值为1,此时BC的长为 ;OA的最大值为2,此时BC的长为 .
第2题解图⑤
题型五 中考新考法试题
【全国视野解读】此题型是对教改文件中提及的改变相对固化的试题形式的落实,通过改变试题形式,同时增加开放性试题,开阔学生思维,拓宽学生眼界.故推荐此题型高效备考.
类型一 结构不良试题
【条件开放】——任选条件进行解答
1. (2023宿迁)在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知:如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上,___________________(填写序号).
求证:BE=DF.
注:如果选择多个条件分别解答,按第一个解答计分.
选②(答案不唯一)
第1题图
第1题图
解:选②(答案不唯一);
证明:∵四边形ABCD是平行四边形,
∴OD=OB,
在△BEO和△DFO中,
∴△BEO △DFO,
∴BE=DF.
≌
【结论开放】——结论不固定,合理即可
2. (2023贵阳)有三个不等式2x+3<-1,-5x>15,3(x-1)>6,请在其中任选两个不等式,组成一个不等式组,并求出它的解集.
解:
∴原不等式组解集为x<-3.(答案不唯一)
3. (2023潍坊)甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为________________________.
y=-2x+1(答案不唯一)
类型二 填空双空题
1. (2023北京)某企业有A,B两条加工相同原材料的生产线.在一天内,A生产线共加工a吨原材料,加工时间为(4a+1)小时;在一天内,B生产线共加工b吨原材料,加工时间为(2b+3)小时.第一天,该企业将5吨原材料分配到A,B两条生产线,两条生产线都在一天内完成了加工,且加工时间相同,则分配到A生产线的吨数与分配到B生产线的吨数的
比为______.
第二天开工前,该企业按第一天的分配结果分配了5吨原材料后,又给A生产线分配了m吨原材料,给B生产线分配了n吨原材料.若两条生产线都能在一天内加工完各自分配到的所有原材料,且加工时间相
同,则 的值为______.
2. (2023嘉兴)如图,在△ABC中,∠BAC=30°, ∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动.连接CP,点A关于直线CP的对称点为A′,连接A′C,A′P.在运动过程中,点A′到直线AB距离的最大值是____________;点P到达点B时,线段
A′P扫过的面积为__________________.
第2题图
类型三 补充依据
1. (2023长沙)人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
已知:△ABC.
求作:△A′B′C′,使得△A′B′C′≌△ABC.
作法:如图.
请你根据以上材料完成下列问题:
(1)完成下面证明过程(将正确答案填在相应的横线上):
证明:由作图可知,在△A′B′C′和△ABC中,
(1)画B′C′=BC;
(2)分别以点B′,C′为圆心,线段AB,AC长为半径画弧,两弧相交于点A′;
(3)连接线段A′B′,A′C′,则△A′B′C′即为所求作的三角形.
∴△A′B′C′ ________.
(2)这种作一个三角形与已知三角形全等的方法的依据是________.(填序号)
①AAS ②ASA ③SAS ④SSS
④
≌
△ABC
AB
AC
2. (2022北京)已知:如图,△ABC为锐角三角形,AB=AC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP= ∠BAC.
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作的线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
第2题图
解:(1)补全图形如解图;
第2题解图
(2)完成下面的证明.
证明:∵CD∥AB,
∴∠ABP=________.
∵AB=AC,
∴点B在A上.
又∵点C,P都在 A上,
∴∠BPC= ∠BAC(__________________________________________
_______________________)(填推理的依据).
∴∠ABP= ∠BAC.
∠CPB
在同圆或等圆中,同弧所对的圆周角等于它所
对的圆心角的一半.
同课章节目录
