3.3中心对称 课件(共29张PPT)
文档属性
| 名称 | 3.3中心对称 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 782.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 13:36:00 | ||
图片预览





文档简介
(共29张PPT)
北师大版 数学 八年级下册
第三章 图形的平移与旋转
3 中心对称
学习目标
1.理解中心对称的定义及性质,会识别中心对称图形.(重点)
2.会运用掌握中心对称及中心对称图形的性质解决实际问题.(重点)
复习回顾
在这之前你学过哪些有关对称的知识?
1.轴对称图形:
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
2.轴对称:
如果两个平面图形沿一条直线折叠后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.
3.轴对称的性质:
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
一、创设情境,引入新知
我们学习了旋转的定义与性质,如果把一个图形绕某点旋转180°,这样的图形运动又有什么特点呢?下面我们一起来探讨.
观察下图,图(1)经过怎样的运动变化就可以与图(2)重合?你还能举出一些类似的例子吗?与同伴交流.
(1) (2) (1) (2)
二、自主合作,探究新知
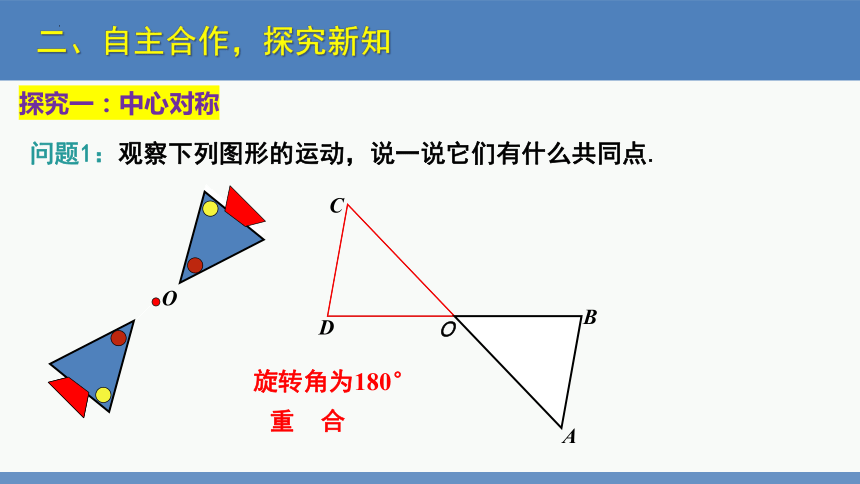
重 合
O
A
O
D
B
C
问题1:观察下列图形的运动,说一说它们有什么共同点.
旋转角为180°
探究一:中心对称
二、自主合作,探究新知
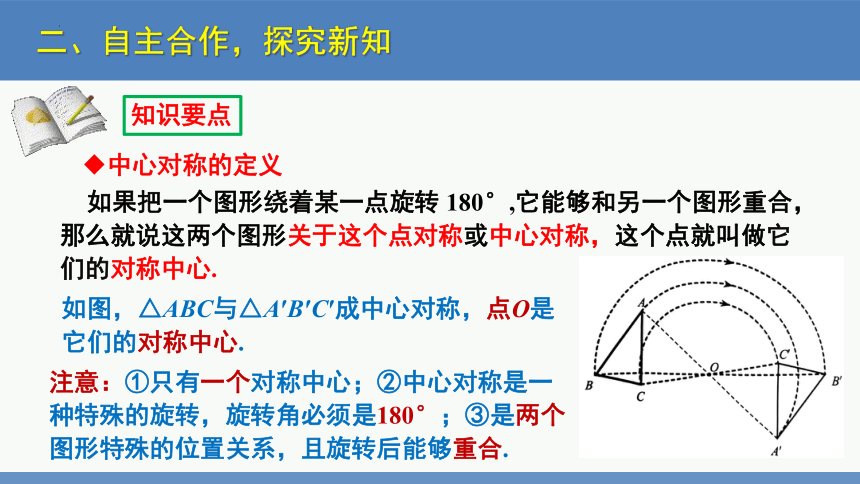
如果把一个图形绕着某一点旋转 180°,它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做它们的对称中心.
注意:①只有一个对称中心;②中心对称是一种特殊的旋转,旋转角必须是180°;③是两个图形特殊的位置关系,且旋转后能够重合.
知识要点
如图,△ABC与△A′B′C′成中心对称,点O是它们的对称中心.
中心对称的定义
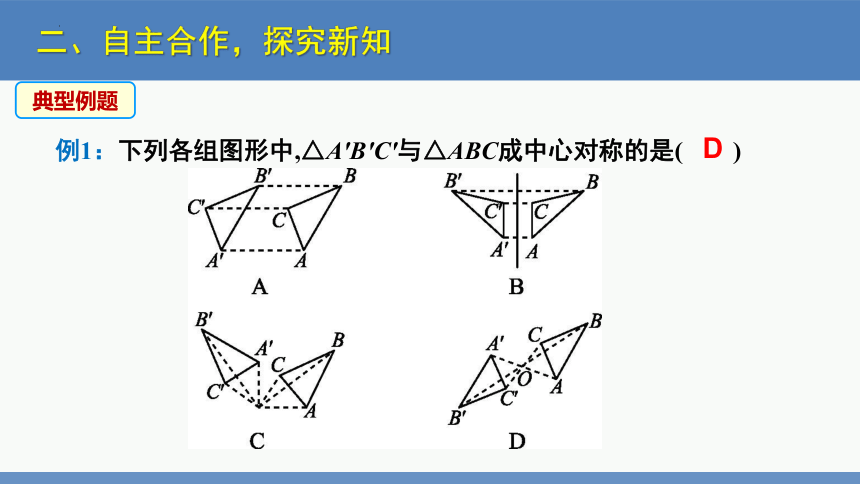
例1:下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
二、自主合作,探究新知
典型例题
D
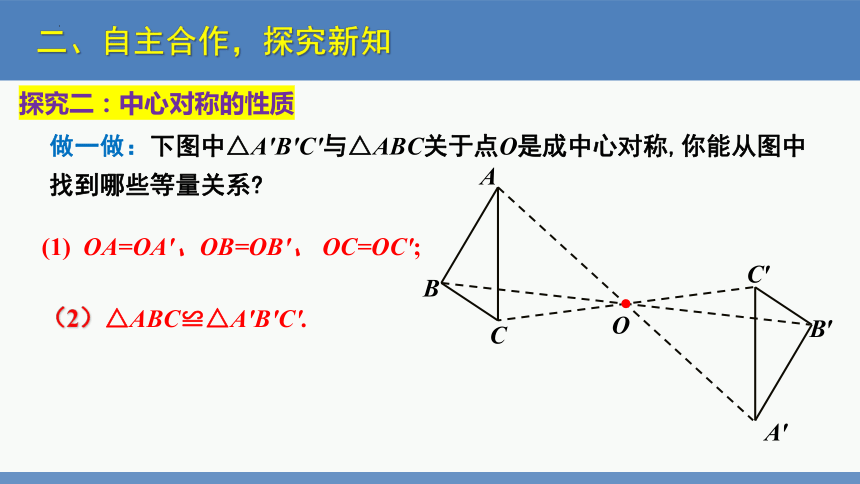
做一做:下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系
A′
B′
C′
A
B
C
O
二、自主合作,探究新知
探究二:中心对称的性质
(1) OA=OA′、OB=OB′、 OC=OC′;
(2)△ABC≌△A′B′C′.
知识要点
二、自主合作,探究新知
1.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
2.成中心对称的两个图形是全等图形.
中心对称的性质
例2:如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
A
B
C
D
E
O
二、自主合作,探究新知
典型例题
解:如图,连接BO并延长到B',使得OB'=OB;
C'
B'
D'
连接CO并延长到点C',使得OC'=OC;
顺次连接AD' ,D'C', C'B',B'E.
图形AD'C'B'E就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
连接DO并延长到点D',使得OD'=OD;
想一想:如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
二、自主合作,探究新知
方法一:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图).
方法二:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
O
注意:如果限制只用直尺作图,我们用方法二.
轴对称 中心对称
不 同 点
二、自主合作,探究新知
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
翻转后和另一个图形重合
旋转后和另一个图形重合
中心对称
1
A
B
C
C
1
A
B
1
O
轴 对 称
思考:中心对称与轴对称有什么不同点?
知识要点
二、自主合作,探究新知
探究三:中心对称图形
共同特征:
绕某一点旋转180°后能与原来图形重合.
议一议:观察下列图形,它们有什么共同特征?你还能举出一些类似的图形吗?
二、自主合作,探究新知
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
O
B
A
C
D
中心对称图形的定义
注意:中心对称图形是指一个图形的特殊性质.
知识要点
中心对称图形的性质:
对称点的连线都经过对称中心,并且被对称中心平分.
想一想:中心对称图形有什么性质呢?
例3:观察下列四个平面图形,其中中心对称图形有( )
A.2个 B.1个 C.4个 D.3个
二、自主合作,探究新知
典型例题
D
(2)在上面例题2中,图形ABCDEB′C′D′是中心对称图形吗
二、自主合作,探究新知
想一想:(1)在你所学过的平面图形中,哪些图形是中心对称图形?
是中心对称图形.
二、自主合作,探究新知
区别:
中心对是指两个全等图形的位置关系;
中心对称图形是指一个图形本身中心对称.
联系:
如果将中心对称的两个图形看成一个整体,则它们是中心对称图形.
如果将中心对称图形对称的两部分看成两个图形,则它们成中心对称.
议一议:中心对称与中心对称图形有什么区别与联系?
知识要点
例4:如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
二、自主合作,探究新知
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3.
3
典型例题
2.已知下列命题,其中正确的个数是 ( )(1)成中心对称的两个图形一定不全等;(2)成中心对称的两个图形是全等图形;(3)两个全等的图形一定成中心对称.A.0 B.1 C.2 D.3
三、即学即练,应用知识
1.下列标志图中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
B
B
3.如图所示的图形是中心对称图形,则其对称中心是( )A.点C B.点D C.线段BC的中点 D.线段FC的中点
4.如图所示,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A'B'C',那么对称中心的坐标为( )A.(0,0) B.(-1,0)
C.(-1,-1) D.(0,-1)
三、即学即练,应用知识
B
D
6.在方格纸中选择标有序号的一个小正方形涂上颜色,与图中阴影部分构成中心对称图形,应选____.
7.如图所示,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C中心对称,则AE的长是 .
三、即学即练,应用知识
5.在①线段, ②角, ③等腰三角形, ④等腰梯形,⑤平行四边形, ⑥矩形, ⑦菱形, ⑧正方形和⑨圆中,是轴对称图形的有_____________________,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④⑥⑦⑧⑨
①⑥⑦⑧⑨
④
8.如图所示,已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形A'B'C'D'.
三、即学即练,应用知识
结论: 如图所示,四边形A'B'C'D'即为所求图形.
A'
B'
C'
D'
四、课堂小结
性质
如果把一个图形绕着某一点旋转 180°,它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做它们的对称中心.
对应点的连线经过对称中心,且被对称中心平分.
中心对称与中心对称图形
中心对称
中心对称图形
定义
性质
定义
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
对称点的连线都经过对称中心,并且被对称中心平分.
2.如图所示,△ABC与△A'B'C'成中心对称,下列说法不正确的是( )A.AB=A'B',AC∥A'C' B.△ABC≌△A'B'C'C.OB=OA',OC=OC' D.∠BAO=∠B'A'O
五、当堂达标检测
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
A
C
4.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( )
A.2 B.4 C.6 D.8
3.点P(m,2)关于原点O的对称点为P'(-3,n),则m,n的值分别为( )A.3,2 B.3,-2
C.-3,2 D.-3,-2
五、当堂达标检测
B
B
5.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 .
6.如图所示,在Rt△ABC中,斜边AB的长为8 cm,直角边BC的长为12 cm.若扇形CAE与扇形DBE关于点E对称,则图中阴影部分的面积是 .
五、当堂达标检测
3
7.如图是由5个全等的小正方形组成的图案,请用两种不同的方法分别在两幅图中各添加1个正方形,使整个图案成为中心对称图形.
五、当堂达标检测
解: 如图所示.
8.如图所示,在平面直角坐标系中,画出△ABC关于原点O成中心对称的△A'B'C'.
五、当堂达标检测
解: △A'B'C'如图所示.
A'
C'
B'
教材习题3.6.
六、布置作业
北师大版 数学 八年级下册
第三章 图形的平移与旋转
3 中心对称
学习目标
1.理解中心对称的定义及性质,会识别中心对称图形.(重点)
2.会运用掌握中心对称及中心对称图形的性质解决实际问题.(重点)
复习回顾
在这之前你学过哪些有关对称的知识?
1.轴对称图形:
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
2.轴对称:
如果两个平面图形沿一条直线折叠后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.
3.轴对称的性质:
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
一、创设情境,引入新知
我们学习了旋转的定义与性质,如果把一个图形绕某点旋转180°,这样的图形运动又有什么特点呢?下面我们一起来探讨.
观察下图,图(1)经过怎样的运动变化就可以与图(2)重合?你还能举出一些类似的例子吗?与同伴交流.
(1) (2) (1) (2)
二、自主合作,探究新知
重 合
O
A
O
D
B
C
问题1:观察下列图形的运动,说一说它们有什么共同点.
旋转角为180°
探究一:中心对称
二、自主合作,探究新知
如果把一个图形绕着某一点旋转 180°,它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做它们的对称中心.
注意:①只有一个对称中心;②中心对称是一种特殊的旋转,旋转角必须是180°;③是两个图形特殊的位置关系,且旋转后能够重合.
知识要点
如图,△ABC与△A′B′C′成中心对称,点O是它们的对称中心.
中心对称的定义
例1:下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
二、自主合作,探究新知
典型例题
D
做一做:下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系
A′
B′
C′
A
B
C
O
二、自主合作,探究新知
探究二:中心对称的性质
(1) OA=OA′、OB=OB′、 OC=OC′;
(2)△ABC≌△A′B′C′.
知识要点
二、自主合作,探究新知
1.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
2.成中心对称的两个图形是全等图形.
中心对称的性质
例2:如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
A
B
C
D
E
O
二、自主合作,探究新知
典型例题
解:如图,连接BO并延长到B',使得OB'=OB;
C'
B'
D'
连接CO并延长到点C',使得OC'=OC;
顺次连接AD' ,D'C', C'B',B'E.
图形AD'C'B'E就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
连接DO并延长到点D',使得OD'=OD;
想一想:如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
二、自主合作,探究新知
方法一:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图).
方法二:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
O
注意:如果限制只用直尺作图,我们用方法二.
轴对称 中心对称
不 同 点
二、自主合作,探究新知
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
翻转后和另一个图形重合
旋转后和另一个图形重合
中心对称
1
A
B
C
C
1
A
B
1
O
轴 对 称
思考:中心对称与轴对称有什么不同点?
知识要点
二、自主合作,探究新知
探究三:中心对称图形
共同特征:
绕某一点旋转180°后能与原来图形重合.
议一议:观察下列图形,它们有什么共同特征?你还能举出一些类似的图形吗?
二、自主合作,探究新知
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
O
B
A
C
D
中心对称图形的定义
注意:中心对称图形是指一个图形的特殊性质.
知识要点
中心对称图形的性质:
对称点的连线都经过对称中心,并且被对称中心平分.
想一想:中心对称图形有什么性质呢?
例3:观察下列四个平面图形,其中中心对称图形有( )
A.2个 B.1个 C.4个 D.3个
二、自主合作,探究新知
典型例题
D
(2)在上面例题2中,图形ABCDEB′C′D′是中心对称图形吗
二、自主合作,探究新知
想一想:(1)在你所学过的平面图形中,哪些图形是中心对称图形?
是中心对称图形.
二、自主合作,探究新知
区别:
中心对是指两个全等图形的位置关系;
中心对称图形是指一个图形本身中心对称.
联系:
如果将中心对称的两个图形看成一个整体,则它们是中心对称图形.
如果将中心对称图形对称的两部分看成两个图形,则它们成中心对称.
议一议:中心对称与中心对称图形有什么区别与联系?
知识要点
例4:如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
二、自主合作,探究新知
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3.
3
典型例题
2.已知下列命题,其中正确的个数是 ( )(1)成中心对称的两个图形一定不全等;(2)成中心对称的两个图形是全等图形;(3)两个全等的图形一定成中心对称.A.0 B.1 C.2 D.3
三、即学即练,应用知识
1.下列标志图中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
B
B
3.如图所示的图形是中心对称图形,则其对称中心是( )A.点C B.点D C.线段BC的中点 D.线段FC的中点
4.如图所示,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A'B'C',那么对称中心的坐标为( )A.(0,0) B.(-1,0)
C.(-1,-1) D.(0,-1)
三、即学即练,应用知识
B
D
6.在方格纸中选择标有序号的一个小正方形涂上颜色,与图中阴影部分构成中心对称图形,应选____.
7.如图所示,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C中心对称,则AE的长是 .
三、即学即练,应用知识
5.在①线段, ②角, ③等腰三角形, ④等腰梯形,⑤平行四边形, ⑥矩形, ⑦菱形, ⑧正方形和⑨圆中,是轴对称图形的有_____________________,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④⑥⑦⑧⑨
①⑥⑦⑧⑨
④
8.如图所示,已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形A'B'C'D'.
三、即学即练,应用知识
结论: 如图所示,四边形A'B'C'D'即为所求图形.
A'
B'
C'
D'
四、课堂小结
性质
如果把一个图形绕着某一点旋转 180°,它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做它们的对称中心.
对应点的连线经过对称中心,且被对称中心平分.
中心对称与中心对称图形
中心对称
中心对称图形
定义
性质
定义
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
对称点的连线都经过对称中心,并且被对称中心平分.
2.如图所示,△ABC与△A'B'C'成中心对称,下列说法不正确的是( )A.AB=A'B',AC∥A'C' B.△ABC≌△A'B'C'C.OB=OA',OC=OC' D.∠BAO=∠B'A'O
五、当堂达标检测
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
A
C
4.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( )
A.2 B.4 C.6 D.8
3.点P(m,2)关于原点O的对称点为P'(-3,n),则m,n的值分别为( )A.3,2 B.3,-2
C.-3,2 D.-3,-2
五、当堂达标检测
B
B
5.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 .
6.如图所示,在Rt△ABC中,斜边AB的长为8 cm,直角边BC的长为12 cm.若扇形CAE与扇形DBE关于点E对称,则图中阴影部分的面积是 .
五、当堂达标检测
3
7.如图是由5个全等的小正方形组成的图案,请用两种不同的方法分别在两幅图中各添加1个正方形,使整个图案成为中心对称图形.
五、当堂达标检测
解: 如图所示.
8.如图所示,在平面直角坐标系中,画出△ABC关于原点O成中心对称的△A'B'C'.
五、当堂达标检测
解: △A'B'C'如图所示.
A'
C'
B'
教材习题3.6.
六、布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
