8.3 一元一次不等式组(教学课件)-七年级数学下册同步精品课堂(华东师大版)
文档属性
| 名称 | 8.3 一元一次不等式组(教学课件)-七年级数学下册同步精品课堂(华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
8.3 一元一次不等式组
数学(华东师大版)
七年级 下册
第8章 一元一次不等式
学习目标
1、通过具体操作,在解一元一次不等式组的过程中形成正确
的解不等式的思路与方法;
2、掌握将一元一次不等式组的解集在数轴上正确的表示;
导入新课
嗨,我听管理员说,这头大象的体重不足5吨呢!
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
x≥3 ①
x<5 ②
讲授新课
知识点一 一元一次不等式组的概念与解集
【问题】 用每分可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么
设用xmin将污水抽完,则x同时满足不等式
30x>1200, ①
30x<1500. ②
讲授新课
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组, 记作
30x>1200, ①
30x<1500. ②
30x>1200,
30x<1500.
怎样确定不等式组中x的可取值的范围呢?
讲授新课
30x>1200,
30x<1500.
由不等式①,解得x>40.
由不等式②,解得x<50.
把不等式①和②的解集在数轴上表示出来(如下图).
40
50
0
x取值的范围为 40<x<50.
这就是说,将污水抽完所用时间多于40min而少于50min.
讲授新课
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
解不等式组就是求它的解集.
讲授新课
典例精析
【例1】解下列不等式组:
(1) (2)
2x-1>x+1,
x+8<4x-1;
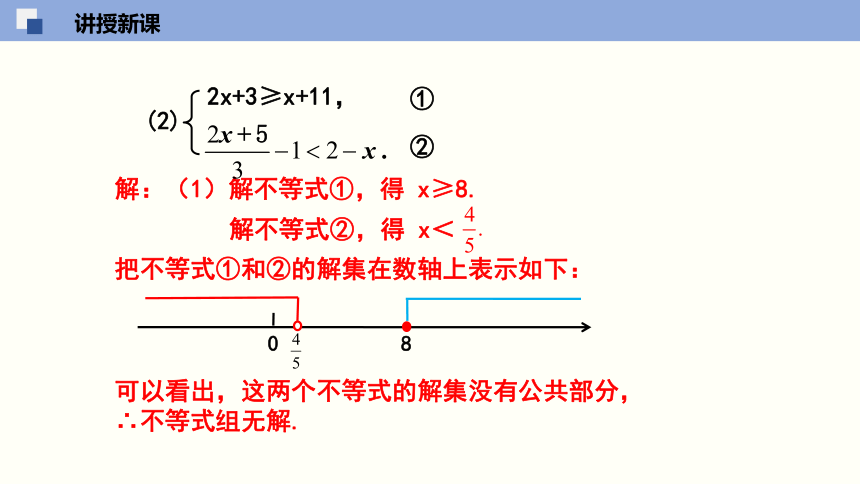
2x+3≥x+11,
①
②
①
②
解:(1)解不等式①,得 x>2.
解不等式②,得 x>3.
把不等式①和②的解集在数轴上表示如下:
∴不等式组的解集为 x>3.
2
3
0
讲授新课
解:(1)解不等式①,得 x≥8.
解不等式②,得 x<
把不等式①和②的解集在数轴上表示如下:
可以看出,这两个不等式的解集没有公共部分,
∴不等式组无解.
(2)
2x+3≥x+11,
①
②
8
0
讲授新课
练一练
1、下列是一元一次不等式组的有________个
(1); (2); (3);
(4); (5).
【分析】
(3)x2+2>4是一元二次不等式,不是一元一次不等式
(4)不等式组中共计有x、y两个元,不符合共计只有一个元的要求
3
(5)一元一次不等式组中不等式的个数可以是两个及以上的任意几个
讲授新课
知识点二 解一元一次不等式组
【例2】解不等式组:
解:
解不等式①,得
解不等式②,得
在同一条数轴上表示不等式① ②的解集,如图:
因此,原不等式组的解集为:
①
②
讲授新课
练一练
1、解不等式组:
解:
解不等式①,得 x>2.5
解不等式②,得 x≥4
在同一条数轴上表示不等式① ②的解集,如图:
0
1
2
3
4
5
6
7
2.5
因此,原不等式组的解集为: x≥4
①
②
讲授新课
2、解不等式组:
解:解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
讲授新课
知识点三 一元一次不等式组的应用
【例3】用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(1)现配制这种饮料10 kg,要求至少含有4 200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
600x+100(10-x) ≥ 4200
讲授新课
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(kg)应满足的另一个不等式吗?
8x+4(10-x)≤72
讲授新课
如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
讲授新课
练一练
1、某中学举办一年一度的商贸街活动,小明同学准备用不超过1054元购进40套考试专用的A,B两种套装,其中A种套装每套进价25元,B种套装每套进价28元,A种每套售价30元,B种每套售价32元,预计销售额不低于1232元,设A种套装购进x套,请你设计出所有的进货方案.
【分析】
设A种套装购进x套,则B种套装购进(40-x)套,
根据题意得:,解得:22≤x≤24,
又∵x为正整数,
∴x可以为22,23,24,
∴小明同学共有3种进货方案,
讲授新课
方案1:购进A种套装22套,B种套装18套;
方案2:购进A种套装23套,B种套装17套;
方案3:购进A种套装24套,B种套装16套.
讲授新课
解一元一次不等式组步骤:
1.求出不等式组中各不等式的解集.
2.将各不等式的解决在数轴上表示出来.
3.在数轴上找出各不等式解集的公共部分,这个公共部分就是不等式组的解集.
当堂检测
1.下列是一元一次不等式组的是( )
D
当堂检测
2.小明要制作一个长方形的相片框架(长、宽不等),这个框架的长为25 cm,面积不小于500 cm2,则宽x(cm)应满足的不等式组为( )
A
当堂检测
3.不等式组 的解集在数轴上表示正确的是( )
D
当堂检测
4.解不等式组: .
解:解不等式4x﹣5>x+1,得:x>2,
解不等式 ,得:x<4,
∴不等式组的解集为2<x<4.
当堂检测
5. 解下列不等式组:
解不等式①,得x> .
解不等式②,得x<3.
所以原不等式组的解集是解不等式①,得x>1.
解不等式②,得x< .
所以原不等式组的解集是1当堂检测
6.用若干载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装满8吨,则最后一辆汽车不满也不空.请问:有多少辆汽车?多少吨货物?
解:设有x辆汽车,则货物有(4x+20)吨
依题意得:0<4x+20-8(x-1)<8
解得:5<x<7
∵x为正整数,∴x=6
货物有4×6+20=44(吨)
答:有汽车6辆,货物44吨
当堂检测
7.为支援抗疫前线,某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为3万元/吨,乙物资单价为2万元/吨,采购两种物资共花费1 380万元.
求甲、乙两种物资各采购了多少吨.
当堂检测
8. 现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元但不低于300元,问有几种购买方案?哪种方案费用最低?
解:(1)设A商品每件x元,B商品每件y元,则 解得
故A每件20元,B每件50元
当堂检测
(2)设购买A商品m件,则购买B商品(10-m)件,依题得
解得:5≤m≤
∵m为整数,
∴m=5或6
方案一:购买A商品5件,B商品5件,总费用为350元;
方案二:购买A商品6件,B商品4件,总费用为320元.
其中方案二费用最低.
课堂小结
1.解不等式组的关键:
一是要正确地求出每个不等式的解集,
二是要利用数轴正确地表示出每个不等式的解集,并找出不等式组的解集.
2.列一元一次不等式组解实际问题的一般步骤:
审题——设元——列不等式(组)——求解——检验——作答.
谢 谢~
8.3 一元一次不等式组
数学(华东师大版)
七年级 下册
第8章 一元一次不等式
学习目标
1、通过具体操作,在解一元一次不等式组的过程中形成正确
的解不等式的思路与方法;
2、掌握将一元一次不等式组的解集在数轴上正确的表示;
导入新课
嗨,我听管理员说,这头大象的体重不足5吨呢!
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
x≥3 ①
x<5 ②
讲授新课
知识点一 一元一次不等式组的概念与解集
【问题】 用每分可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么
设用xmin将污水抽完,则x同时满足不等式
30x>1200, ①
30x<1500. ②
讲授新课
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组, 记作
30x>1200, ①
30x<1500. ②
30x>1200,
30x<1500.
怎样确定不等式组中x的可取值的范围呢?
讲授新课
30x>1200,
30x<1500.
由不等式①,解得x>40.
由不等式②,解得x<50.
把不等式①和②的解集在数轴上表示出来(如下图).
40
50
0
x取值的范围为 40<x<50.
这就是说,将污水抽完所用时间多于40min而少于50min.
讲授新课
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
解不等式组就是求它的解集.
讲授新课
典例精析
【例1】解下列不等式组:
(1) (2)
2x-1>x+1,
x+8<4x-1;
2x+3≥x+11,
①
②
①
②
解:(1)解不等式①,得 x>2.
解不等式②,得 x>3.
把不等式①和②的解集在数轴上表示如下:
∴不等式组的解集为 x>3.
2
3
0
讲授新课
解:(1)解不等式①,得 x≥8.
解不等式②,得 x<
把不等式①和②的解集在数轴上表示如下:
可以看出,这两个不等式的解集没有公共部分,
∴不等式组无解.
(2)
2x+3≥x+11,
①
②
8
0
讲授新课
练一练
1、下列是一元一次不等式组的有________个
(1); (2); (3);
(4); (5).
【分析】
(3)x2+2>4是一元二次不等式,不是一元一次不等式
(4)不等式组中共计有x、y两个元,不符合共计只有一个元的要求
3
(5)一元一次不等式组中不等式的个数可以是两个及以上的任意几个
讲授新课
知识点二 解一元一次不等式组
【例2】解不等式组:
解:
解不等式①,得
解不等式②,得
在同一条数轴上表示不等式① ②的解集,如图:
因此,原不等式组的解集为:
①
②
讲授新课
练一练
1、解不等式组:
解:
解不等式①,得 x>2.5
解不等式②,得 x≥4
在同一条数轴上表示不等式① ②的解集,如图:
0
1
2
3
4
5
6
7
2.5
因此,原不等式组的解集为: x≥4
①
②
讲授新课
2、解不等式组:
解:解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
讲授新课
知识点三 一元一次不等式组的应用
【例3】用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(1)现配制这种饮料10 kg,要求至少含有4 200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
600x+100(10-x) ≥ 4200
讲授新课
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(kg)应满足的另一个不等式吗?
8x+4(10-x)≤72
讲授新课
如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
讲授新课
练一练
1、某中学举办一年一度的商贸街活动,小明同学准备用不超过1054元购进40套考试专用的A,B两种套装,其中A种套装每套进价25元,B种套装每套进价28元,A种每套售价30元,B种每套售价32元,预计销售额不低于1232元,设A种套装购进x套,请你设计出所有的进货方案.
【分析】
设A种套装购进x套,则B种套装购进(40-x)套,
根据题意得:,解得:22≤x≤24,
又∵x为正整数,
∴x可以为22,23,24,
∴小明同学共有3种进货方案,
讲授新课
方案1:购进A种套装22套,B种套装18套;
方案2:购进A种套装23套,B种套装17套;
方案3:购进A种套装24套,B种套装16套.
讲授新课
解一元一次不等式组步骤:
1.求出不等式组中各不等式的解集.
2.将各不等式的解决在数轴上表示出来.
3.在数轴上找出各不等式解集的公共部分,这个公共部分就是不等式组的解集.
当堂检测
1.下列是一元一次不等式组的是( )
D
当堂检测
2.小明要制作一个长方形的相片框架(长、宽不等),这个框架的长为25 cm,面积不小于500 cm2,则宽x(cm)应满足的不等式组为( )
A
当堂检测
3.不等式组 的解集在数轴上表示正确的是( )
D
当堂检测
4.解不等式组: .
解:解不等式4x﹣5>x+1,得:x>2,
解不等式 ,得:x<4,
∴不等式组的解集为2<x<4.
当堂检测
5. 解下列不等式组:
解不等式①,得x> .
解不等式②,得x<3.
所以原不等式组的解集是
解不等式②,得x< .
所以原不等式组的解集是1
6.用若干载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装满8吨,则最后一辆汽车不满也不空.请问:有多少辆汽车?多少吨货物?
解:设有x辆汽车,则货物有(4x+20)吨
依题意得:0<4x+20-8(x-1)<8
解得:5<x<7
∵x为正整数,∴x=6
货物有4×6+20=44(吨)
答:有汽车6辆,货物44吨
当堂检测
7.为支援抗疫前线,某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为3万元/吨,乙物资单价为2万元/吨,采购两种物资共花费1 380万元.
求甲、乙两种物资各采购了多少吨.
当堂检测
8. 现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元但不低于300元,问有几种购买方案?哪种方案费用最低?
解:(1)设A商品每件x元,B商品每件y元,则 解得
故A每件20元,B每件50元
当堂检测
(2)设购买A商品m件,则购买B商品(10-m)件,依题得
解得:5≤m≤
∵m为整数,
∴m=5或6
方案一:购买A商品5件,B商品5件,总费用为350元;
方案二:购买A商品6件,B商品4件,总费用为320元.
其中方案二费用最低.
课堂小结
1.解不等式组的关键:
一是要正确地求出每个不等式的解集,
二是要利用数轴正确地表示出每个不等式的解集,并找出不等式组的解集.
2.列一元一次不等式组解实际问题的一般步骤:
审题——设元——列不等式(组)——求解——检验——作答.
谢 谢~
