10.3.3解二元一次方程组-解的个数问题&同解问题&错解问题(同步课件)-七年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 10.3.3解二元一次方程组-解的个数问题&同解问题&错解问题(同步课件)-七年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 09:42:38 | ||
图片预览











文档简介
(共36张PPT)
第10章二元一次方程组
10.3.3解二元一次方程组-解的个数问题&同解问题&错解问题
教学目标
01
掌握二元一次方程组的解的个数问题,区分唯一解、无数个解、无解所需具备的条件
02
理解同解方程组的概念,掌握同解问题的处理方法
03
掌握错解问题的处理方法
解的个数问题
Q:讨论关于x的方程ax=b的解的情况~
【分析】
方程ax=b的解由a、b的值决定:
01
复习引入
(1)若a≠0,则方程ax=b有唯一解x=;
(2)若a=b=0,方程变形为0·x=0,则方程ax=b有无数个解;
(3)若a=0,b≠0,方程变为0·x=b,则方程无解。
01
情境引入
Q1-1:观察下列方程组,每个方程组中两个方程等号左边的部分成比例吗?
(1), (2)。
【分析】每个方程组中两个方程等号左边的部分不成比例。
01
情境引入
Q1-2:解方程组:
(1), (2)。
【分析】
(1)由①×2-②得:y=0,
将y=0代入①得:2x=4,
解得:x=2,
∴原方程组的解为;
(2)由①×3-②得:y=1,
将y=1代入①得:x+3=2,
解得:x=-1,
∴原方程组的解为。
01
情境引入
有唯一解
Q1-3:已知二元一次方程组,若≠,则方方程组的解的情况为:__________。
01
情境引入
Q2-1:观察下列方程组,你发现了什么?
(1); (2)。
【分析】
每个方程组中对应的两个方程成比例:
(1)②=①×2; (2)②=①×3。
Q2-2:完成下列表格,你发现了什么?
2x+3y=4 x … 1 2 3 4 5 6 …
y … …
【分析】2x+3y=4与4x+6y=8的解完全相同。
01
情境引入
- - - -
4x+6y=8 x … 1 2 3 4 5 6 …
y … …
- - - -
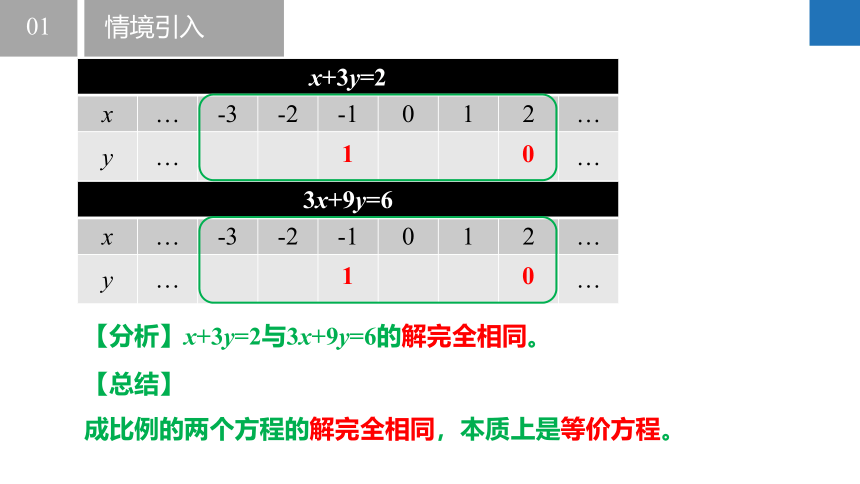
x+3y=2 x … -3 -2 -1 0 1 2 …
y … …
【总结】
成比例的两个方程的解完全相同,本质上是等价方程。
01
情境引入
1 0
3x+9y=6 x … -3 -2 -1 0 1 2 …
y … …
1 0
【分析】x+3y=2与3x+9y=6的解完全相同。
01
情境引入
2x+3y=4&4x+6y=8 x … 1 2 3 4 5 6 …
y … - - - - …
【分析】方程组的解有无数个,为:
…,,,,,,,…
Q2-3:方程组、的解分别为?
01
情境引入
【分析】方程组的解有无数个,为:
…,,,,,,,…
x+3y=2&3x+9y=6 x … -3 -2 -1 0 1 2 …
y … 1 0 …
01
情境引入
Q2-4:已知二元一次方程组,若==,则方程组的解的情况为:___________。
有无数个解
【分析】每个方程组中对应的两个方程不成比例,但是等号左边的部分成比例。
01
情境引入
Q3-1:观察下列方程组,你发现了什么?
(1); (2)。
01
情境引入
Q3-2:你能求出下列方程组的解吗?
(1); (2)。
【分析】
(1)由①×2得:4x+6y=8,
与4x+6y=520矛盾,
故两个方程没有公共解,
∴方程组无解;
(2)由①×3得:3x+9y=6,
与3x+9y=1314矛盾,
故两个方程没有公共解,
∴方程组无解。
01
情境引入
Q3-3:已知二元一次方程组,若=≠,则方程组的解的情况为:________。
无解
02
知识精讲
解的个数问题
【二元一次方程组的解的情况】
方程组的解的个数与、、的值有关:
(1)若≠,则方程组有唯一解;
(2)若==,则方程组有无数个解;
(3)若=≠,则方程组无解。
02
知识精讲
议一议:选择一组a、c的值使关于x、y的二元一次方程组,(1)有无数个解;(2)无解。
【分析】
(1)∵有无数个解,
∴==,
∴==,解得:;
(2)∵无解,
∴=≠,
∴=≠,解得:,
则可选择一组a、c的值为。
例1、若要关于x、y的二元一次方程组有无数个解,求a的值。
03
典例精析
【分析】
∵有无数个解,∴==,
∴==,解得:a=12。
例2、若要关于x、y的二元一次方程组无解,求a和c应满足的条件。
03
典例精析
【分析】
∵无解,∴=≠,
∴=≠,解得:,
∴a和c应满足的条件为。
同解问题
两个方程组的解相同。
01
情境引入
【分析】;;
Q1:方程组的解为?方程组的解为?
你发现了什么?
01
情境引入
Q2:交换两个方程组中一元二次方程的partner,则方程组的解为?方程组的解为?你发现了什么?
【分析】;;
两个方程组的解仍然相同,且仍为刚刚的解。
【同解方程组】
如果两个方程组的解相同,那么这两个方程组就是同解方程组。
同解方程组的四个方程都有同一组公共解,即随便把其中两个方程联立成方程组,解仍然相同。
02
知识精讲
同解方程组
02
知识精讲
议一议1:若方程组与方程组同解,则mn=________。
8
【分析】,①+②得:2x=4,解得:x=2,
将x=2代入①得:2+y=3,解得:y=1,
将x=2,y=1代入方程组得:,
解得:m=4,n=2,∴mn=8。
02
知识精讲
议一议2:若方程组与方程组的解相等,试求a、b的值。
【分析】∵方程组与方程组的解相等,
∴、与原方程组同解,
①+②得:6x=12,解得:x=2,
将x=2代入①得:4+3y=10,解得:y=2,
02
知识精讲
【分析】∵方程组与方程组的解相等,
∴、与原方程组同解,
①+②得:6x=12,解得:x=2,
将x=2代入①得:4+3y=10,解得:y=2,
将x=2,y=2代入得:,
③+④得:4b=17,解得:b=,
将b=代入③得:2a+=9,解得:a=。
例、已知方程组与有相同的解,求m、n的值。
03
典例精析
由①+②×3得:13y=13,解得:y=1,
将y=1代入①得:3x-2=4,解得:x=2,
【分析】∵方程组与有相同的解,
∴、与原方程组同解,
【分析】∵方程组与有相同的解,
∴、与原方程组同解,
由①+②×3得:13y=13,解得:y=1,
将y=1代入①得:3x-2=4,解得:x=2,
将x=2,y=1代入得:,
③×3+④得:10m=40,解得:m=4,
将m=4代入③得:8+n=7,解得:n=-1。
03
典例精析
错解问题
【分析】
将x=2,y=1代入②得:6-b=2,解得:b=4,
将x=3,y=-1代入①得:3a-3=9,解得:a=4。
02
知识精讲
议一议1:两位同学在解关于x、y的方程组时,甲看错①中的a,解得x=2,y=1,乙看错②中的b,解得x=3,y=-1,那么a和b的正确值应是________。
02
知识精讲
议一议2:甲乙两人同时解方程组,甲正确解得;乙因抄错了c,解得;则a=____,b=____,c=____。
【分析】将代入cx-3y=-2得:c-3=-2,解得:c=1;
2
0
1
将代入ax+by=2得:a+b=2,将代入ax+by=2得:a-b=2,
联立,解得:。
例1、甲乙两人同时解方程组,甲同学因看错了b的符号,从而求得解为,乙同学因看漏了c,从而求得解为,试求(b+c)a的值。
03
典例精析
【分析】将代入cx-y=4得:3c-2=4,解得:c=2;
将代入ax+by=13得:3a+2b=13,将代入ax-by=13得:5a-b=13,
联立,解得:,
∴(b+c)a=(2+2)3=64。
例2、在解方程组时,由于粗心,甲看错了①中的a,而得解为;乙看错了②中的b,而得解为。
(1)求出原方程组的正确解;
(2)甲把a看成的数是多少?乙把b看成的数是多少?
03
典例精析
【分析】(1)将代入②得:-12+b=-2,解得:b=10,
将代入①得:5a+20=15,解得:a=-1,
∴原方程组为,解得:。
例2、在解方程组时,由于粗心,甲看错了①中的a,而得解为;乙看错了②中的b,而得解为。
(1)求出原方程组的正确解;
(2)甲把a看成的数是多少?乙把b看成的数是多少?
03
典例精析
(2)将代入①得:-3a’-5=15,解得:a’=-,
将代入②得:20-4b’=-2,解得:b’=,
∴甲把a看成的数是-,乙把b看成的数是。
课后总结
【二元一次方程组的解的情况】
方程组的解的个数与、、的值有关:
(1)若≠,则方程组有唯一解;
(2)若==,则方程组有无数个解;
(3)若=≠,则方程组无解。
【同解方程组】
如果两个方程组的解相同,那么这两个方程组就是同解方程组。
同解方程组的四个方程都有同一组公共解,即随便把其中两个方程联立成方程组,解仍然相同。
第10章二元一次方程组
10.3.3解二元一次方程组-解的个数问题&同解问题&错解问题
教学目标
01
掌握二元一次方程组的解的个数问题,区分唯一解、无数个解、无解所需具备的条件
02
理解同解方程组的概念,掌握同解问题的处理方法
03
掌握错解问题的处理方法
解的个数问题
Q:讨论关于x的方程ax=b的解的情况~
【分析】
方程ax=b的解由a、b的值决定:
01
复习引入
(1)若a≠0,则方程ax=b有唯一解x=;
(2)若a=b=0,方程变形为0·x=0,则方程ax=b有无数个解;
(3)若a=0,b≠0,方程变为0·x=b,则方程无解。
01
情境引入
Q1-1:观察下列方程组,每个方程组中两个方程等号左边的部分成比例吗?
(1), (2)。
【分析】每个方程组中两个方程等号左边的部分不成比例。
01
情境引入
Q1-2:解方程组:
(1), (2)。
【分析】
(1)由①×2-②得:y=0,
将y=0代入①得:2x=4,
解得:x=2,
∴原方程组的解为;
(2)由①×3-②得:y=1,
将y=1代入①得:x+3=2,
解得:x=-1,
∴原方程组的解为。
01
情境引入
有唯一解
Q1-3:已知二元一次方程组,若≠,则方方程组的解的情况为:__________。
01
情境引入
Q2-1:观察下列方程组,你发现了什么?
(1); (2)。
【分析】
每个方程组中对应的两个方程成比例:
(1)②=①×2; (2)②=①×3。
Q2-2:完成下列表格,你发现了什么?
2x+3y=4 x … 1 2 3 4 5 6 …
y … …
【分析】2x+3y=4与4x+6y=8的解完全相同。
01
情境引入
- - - -
4x+6y=8 x … 1 2 3 4 5 6 …
y … …
- - - -
x+3y=2 x … -3 -2 -1 0 1 2 …
y … …
【总结】
成比例的两个方程的解完全相同,本质上是等价方程。
01
情境引入
1 0
3x+9y=6 x … -3 -2 -1 0 1 2 …
y … …
1 0
【分析】x+3y=2与3x+9y=6的解完全相同。
01
情境引入
2x+3y=4&4x+6y=8 x … 1 2 3 4 5 6 …
y … - - - - …
【分析】方程组的解有无数个,为:
…,,,,,,,…
Q2-3:方程组、的解分别为?
01
情境引入
【分析】方程组的解有无数个,为:
…,,,,,,,…
x+3y=2&3x+9y=6 x … -3 -2 -1 0 1 2 …
y … 1 0 …
01
情境引入
Q2-4:已知二元一次方程组,若==,则方程组的解的情况为:___________。
有无数个解
【分析】每个方程组中对应的两个方程不成比例,但是等号左边的部分成比例。
01
情境引入
Q3-1:观察下列方程组,你发现了什么?
(1); (2)。
01
情境引入
Q3-2:你能求出下列方程组的解吗?
(1); (2)。
【分析】
(1)由①×2得:4x+6y=8,
与4x+6y=520矛盾,
故两个方程没有公共解,
∴方程组无解;
(2)由①×3得:3x+9y=6,
与3x+9y=1314矛盾,
故两个方程没有公共解,
∴方程组无解。
01
情境引入
Q3-3:已知二元一次方程组,若=≠,则方程组的解的情况为:________。
无解
02
知识精讲
解的个数问题
【二元一次方程组的解的情况】
方程组的解的个数与、、的值有关:
(1)若≠,则方程组有唯一解;
(2)若==,则方程组有无数个解;
(3)若=≠,则方程组无解。
02
知识精讲
议一议:选择一组a、c的值使关于x、y的二元一次方程组,(1)有无数个解;(2)无解。
【分析】
(1)∵有无数个解,
∴==,
∴==,解得:;
(2)∵无解,
∴=≠,
∴=≠,解得:,
则可选择一组a、c的值为。
例1、若要关于x、y的二元一次方程组有无数个解,求a的值。
03
典例精析
【分析】
∵有无数个解,∴==,
∴==,解得:a=12。
例2、若要关于x、y的二元一次方程组无解,求a和c应满足的条件。
03
典例精析
【分析】
∵无解,∴=≠,
∴=≠,解得:,
∴a和c应满足的条件为。
同解问题
两个方程组的解相同。
01
情境引入
【分析】;;
Q1:方程组的解为?方程组的解为?
你发现了什么?
01
情境引入
Q2:交换两个方程组中一元二次方程的partner,则方程组的解为?方程组的解为?你发现了什么?
【分析】;;
两个方程组的解仍然相同,且仍为刚刚的解。
【同解方程组】
如果两个方程组的解相同,那么这两个方程组就是同解方程组。
同解方程组的四个方程都有同一组公共解,即随便把其中两个方程联立成方程组,解仍然相同。
02
知识精讲
同解方程组
02
知识精讲
议一议1:若方程组与方程组同解,则mn=________。
8
【分析】,①+②得:2x=4,解得:x=2,
将x=2代入①得:2+y=3,解得:y=1,
将x=2,y=1代入方程组得:,
解得:m=4,n=2,∴mn=8。
02
知识精讲
议一议2:若方程组与方程组的解相等,试求a、b的值。
【分析】∵方程组与方程组的解相等,
∴、与原方程组同解,
①+②得:6x=12,解得:x=2,
将x=2代入①得:4+3y=10,解得:y=2,
02
知识精讲
【分析】∵方程组与方程组的解相等,
∴、与原方程组同解,
①+②得:6x=12,解得:x=2,
将x=2代入①得:4+3y=10,解得:y=2,
将x=2,y=2代入得:,
③+④得:4b=17,解得:b=,
将b=代入③得:2a+=9,解得:a=。
例、已知方程组与有相同的解,求m、n的值。
03
典例精析
由①+②×3得:13y=13,解得:y=1,
将y=1代入①得:3x-2=4,解得:x=2,
【分析】∵方程组与有相同的解,
∴、与原方程组同解,
【分析】∵方程组与有相同的解,
∴、与原方程组同解,
由①+②×3得:13y=13,解得:y=1,
将y=1代入①得:3x-2=4,解得:x=2,
将x=2,y=1代入得:,
③×3+④得:10m=40,解得:m=4,
将m=4代入③得:8+n=7,解得:n=-1。
03
典例精析
错解问题
【分析】
将x=2,y=1代入②得:6-b=2,解得:b=4,
将x=3,y=-1代入①得:3a-3=9,解得:a=4。
02
知识精讲
议一议1:两位同学在解关于x、y的方程组时,甲看错①中的a,解得x=2,y=1,乙看错②中的b,解得x=3,y=-1,那么a和b的正确值应是________。
02
知识精讲
议一议2:甲乙两人同时解方程组,甲正确解得;乙因抄错了c,解得;则a=____,b=____,c=____。
【分析】将代入cx-3y=-2得:c-3=-2,解得:c=1;
2
0
1
将代入ax+by=2得:a+b=2,将代入ax+by=2得:a-b=2,
联立,解得:。
例1、甲乙两人同时解方程组,甲同学因看错了b的符号,从而求得解为,乙同学因看漏了c,从而求得解为,试求(b+c)a的值。
03
典例精析
【分析】将代入cx-y=4得:3c-2=4,解得:c=2;
将代入ax+by=13得:3a+2b=13,将代入ax-by=13得:5a-b=13,
联立,解得:,
∴(b+c)a=(2+2)3=64。
例2、在解方程组时,由于粗心,甲看错了①中的a,而得解为;乙看错了②中的b,而得解为。
(1)求出原方程组的正确解;
(2)甲把a看成的数是多少?乙把b看成的数是多少?
03
典例精析
【分析】(1)将代入②得:-12+b=-2,解得:b=10,
将代入①得:5a+20=15,解得:a=-1,
∴原方程组为,解得:。
例2、在解方程组时,由于粗心,甲看错了①中的a,而得解为;乙看错了②中的b,而得解为。
(1)求出原方程组的正确解;
(2)甲把a看成的数是多少?乙把b看成的数是多少?
03
典例精析
(2)将代入①得:-3a’-5=15,解得:a’=-,
将代入②得:20-4b’=-2,解得:b’=,
∴甲把a看成的数是-,乙把b看成的数是。
课后总结
【二元一次方程组的解的情况】
方程组的解的个数与、、的值有关:
(1)若≠,则方程组有唯一解;
(2)若==,则方程组有无数个解;
(3)若=≠,则方程组无解。
【同解方程组】
如果两个方程组的解相同,那么这两个方程组就是同解方程组。
同解方程组的四个方程都有同一组公共解,即随便把其中两个方程联立成方程组,解仍然相同。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
