14.1三角形的分类(第2课时) 课件(共22张PPT)
文档属性
| 名称 | 14.1三角形的分类(第2课时) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
14.1三角形的分类
(第2课时)
2023-2024学年沪教版七年级下册数学课件
思考
如图14-3,各三角形的内角有什么特征
观察图14-3中各三角形的三个内角,可以发现,三角形ABC 的三个内角均为锐角;三角形 DEF有一个内角是直角;三角形 GHI有一个内角是钝角.
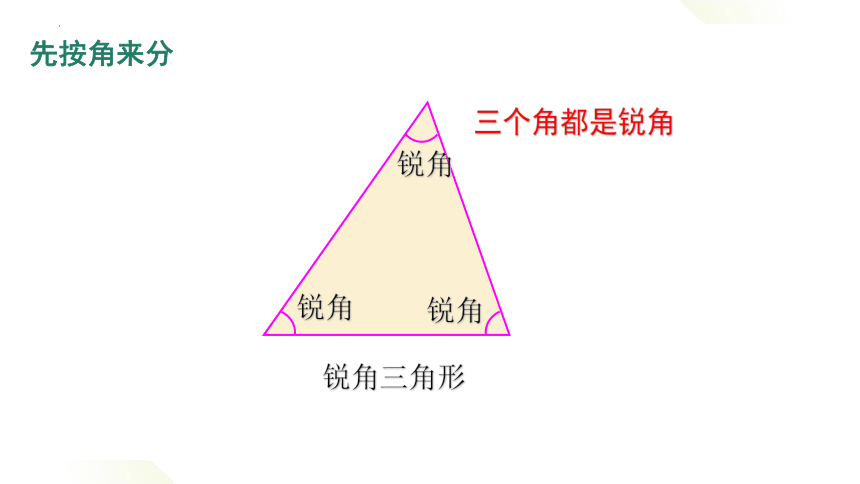
锐角三角形
三个角都是锐角
锐角
锐角
锐角
先按角来分
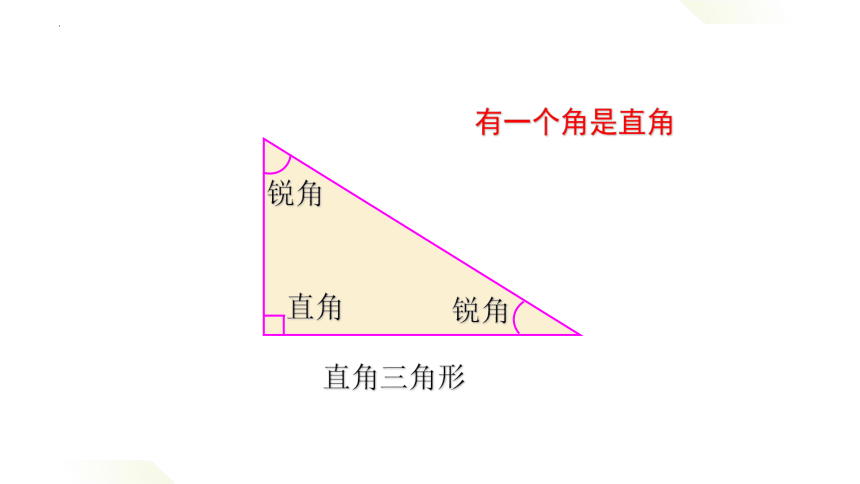
直角三角形
有一个角是直角
锐角
锐角
直角
钝角三角形
有一个角是钝角
锐角
锐角
钝角
三个内角都是锐角的三角形叫做锐角三角形(acute triangle);
有一个内角是直角的三角形叫做直角三角形 (right triangle) ;
有一个内角是钝角的三角形叫做钝角三角形(obtuse triangle)
90°
150°
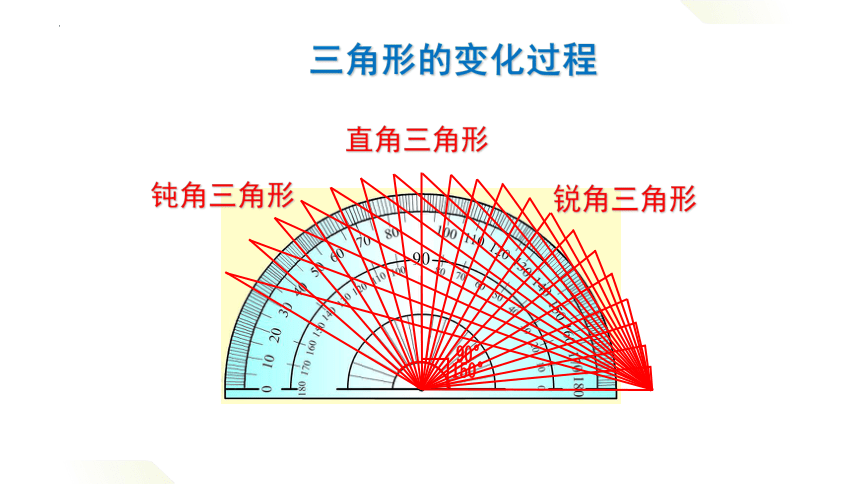
锐角三角形
直角三角形
钝角三角形
三角形的变化过程
①
②
③
④
⑤
⑥
根据三角形的组成元素,尝试对以下三角形进行分类,并说说你的分类标准.
锐角三角形
直角三角形
钝角三角形
直角三角形
钝角三角形
锐角三角形
三角形按照角的大小分类:
三角形
锐角三角形
直角三角形
钝角三角形
三角形按角分类 名称 锐角三角形 钝角三角形 直角三角形
图形
特点 三个锐角 一个钝角 一个直角
6
7
4
5
1
2
3
你能找出下列三角形各自的特点吗?
不等边三角形
等腰三角形
等边三角形
三条边各不相等的三角形叫做不等边三角形 .
有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角
三条边都相等的三角形叫做等边三角形.
再按边来分
等边三角形
等腰三角形
不等边三角形
名称
三条边都相等
只有两条边相等
三条边都不相等
特点
图形
三角形按边分类
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
等边三角形
( 是等腰三角形的特例)
思考
我们使用的有45°角的三角板是什么类型的三角形
1.下列说法正确的是( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;
③等腰三角形至少有两条边相等.
A.①②③ B.②③ C.①③ D.③
D
2. 已知△ABC的三边长分别是a,b,c, 且(a-b)(b-c) (c-a)=0,则△ABC是( )
A. 等腰三角形
B. 等边三角形
C. 三边都不相等的三角形
D. 底边和腰不相等的等腰三角形
A
3.根据下列所给条件,判断△ABC的形状(若已知的是角,则按角的分类标准去判断;若已知的是边,则按边的分类标准去判断):
(1)∠A=45°,∠B=65°,∠C=70°;
(2)∠C=120°;(3)∠C=90°;
(4)AB=BC=4,AC=5.
(1)∠A=45°,∠B=65°,∠C=70°;
(2)∠C=120°;
解:∵∠A=45°,∠B=65°,∠C=70°,
∴∠A<∠B<∠C< 90°,∴△ABC是锐角三角形.
∵∠C=120°>90°,∴△ABC是钝角三角形.
(3)∠C=90°;
(4)AB=BC=4,AC=5.
解:∵∠C=90°,∴△ABC是直角三角形.
∵ AB=BC=4,AC=5,∴△ABC是等腰三角形.
4.已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状;
解:因为(a-b)2+(b-c)2=0,
所以a-b=0,b-c=0,即a=b=c,
所以△ABC是等边三角形.
(2)若a=5,b=2,且c为整数,求△ABC 的周长的最大值及最小值.
解:由三角形三边关系可知5-2<c<5+2,
即3<c<7,
因为c为整数,所以c最大值=6,c最小值=4,
所以△ABC的周长的最大值为5+2+6=13,
最小值为5+2+4=11.
5.如图,P是△ABC内部的一点.
(1)度量AB,AC,PB,PC的长,根据度量结果比较AB+AC与PB+PC的大小;
解:度量结果略.
AB+AC>PB+PC.
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么成立吗?
解:成立.
解:如图,延长BP交AC于点D.
在△ABD中,AB+AD>PB+PD;①
在△PDC中,PD+DC>PC.②
①+②,得AB+AD+PD+DC>PB+PD+PC,
即AB+AC>PB+PC.
谢谢
14.1三角形的分类
(第2课时)
2023-2024学年沪教版七年级下册数学课件
思考
如图14-3,各三角形的内角有什么特征
观察图14-3中各三角形的三个内角,可以发现,三角形ABC 的三个内角均为锐角;三角形 DEF有一个内角是直角;三角形 GHI有一个内角是钝角.
锐角三角形
三个角都是锐角
锐角
锐角
锐角
先按角来分
直角三角形
有一个角是直角
锐角
锐角
直角
钝角三角形
有一个角是钝角
锐角
锐角
钝角
三个内角都是锐角的三角形叫做锐角三角形(acute triangle);
有一个内角是直角的三角形叫做直角三角形 (right triangle) ;
有一个内角是钝角的三角形叫做钝角三角形(obtuse triangle)
90°
150°
锐角三角形
直角三角形
钝角三角形
三角形的变化过程
①
②
③
④
⑤
⑥
根据三角形的组成元素,尝试对以下三角形进行分类,并说说你的分类标准.
锐角三角形
直角三角形
钝角三角形
直角三角形
钝角三角形
锐角三角形
三角形按照角的大小分类:
三角形
锐角三角形
直角三角形
钝角三角形
三角形按角分类 名称 锐角三角形 钝角三角形 直角三角形
图形
特点 三个锐角 一个钝角 一个直角
6
7
4
5
1
2
3
你能找出下列三角形各自的特点吗?
不等边三角形
等腰三角形
等边三角形
三条边各不相等的三角形叫做不等边三角形 .
有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角
三条边都相等的三角形叫做等边三角形.
再按边来分
等边三角形
等腰三角形
不等边三角形
名称
三条边都相等
只有两条边相等
三条边都不相等
特点
图形
三角形按边分类
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
等边三角形
( 是等腰三角形的特例)
思考
我们使用的有45°角的三角板是什么类型的三角形
1.下列说法正确的是( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;
③等腰三角形至少有两条边相等.
A.①②③ B.②③ C.①③ D.③
D
2. 已知△ABC的三边长分别是a,b,c, 且(a-b)(b-c) (c-a)=0,则△ABC是( )
A. 等腰三角形
B. 等边三角形
C. 三边都不相等的三角形
D. 底边和腰不相等的等腰三角形
A
3.根据下列所给条件,判断△ABC的形状(若已知的是角,则按角的分类标准去判断;若已知的是边,则按边的分类标准去判断):
(1)∠A=45°,∠B=65°,∠C=70°;
(2)∠C=120°;(3)∠C=90°;
(4)AB=BC=4,AC=5.
(1)∠A=45°,∠B=65°,∠C=70°;
(2)∠C=120°;
解:∵∠A=45°,∠B=65°,∠C=70°,
∴∠A<∠B<∠C< 90°,∴△ABC是锐角三角形.
∵∠C=120°>90°,∴△ABC是钝角三角形.
(3)∠C=90°;
(4)AB=BC=4,AC=5.
解:∵∠C=90°,∴△ABC是直角三角形.
∵ AB=BC=4,AC=5,∴△ABC是等腰三角形.
4.已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状;
解:因为(a-b)2+(b-c)2=0,
所以a-b=0,b-c=0,即a=b=c,
所以△ABC是等边三角形.
(2)若a=5,b=2,且c为整数,求△ABC 的周长的最大值及最小值.
解:由三角形三边关系可知5-2<c<5+2,
即3<c<7,
因为c为整数,所以c最大值=6,c最小值=4,
所以△ABC的周长的最大值为5+2+6=13,
最小值为5+2+4=11.
5.如图,P是△ABC内部的一点.
(1)度量AB,AC,PB,PC的长,根据度量结果比较AB+AC与PB+PC的大小;
解:度量结果略.
AB+AC>PB+PC.
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么成立吗?
解:成立.
解:如图,延长BP交AC于点D.
在△ABD中,AB+AD>PB+PD;①
在△PDC中,PD+DC>PC.②
①+②,得AB+AD+PD+DC>PB+PD+PC,
即AB+AC>PB+PC.
谢谢
