14.2三角形的内角和性质与外角和性质应用(第3课时) 课件(共23张PPT)
文档属性
| 名称 | 14.2三角形的内角和性质与外角和性质应用(第3课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 21:06:48 | ||
图片预览





文档简介
(共23张PPT)
14.2三角形的内角和性质与外角和性质应用(第3课时)
2023-2024学年沪教版七年级下册数学课件
知识回顾
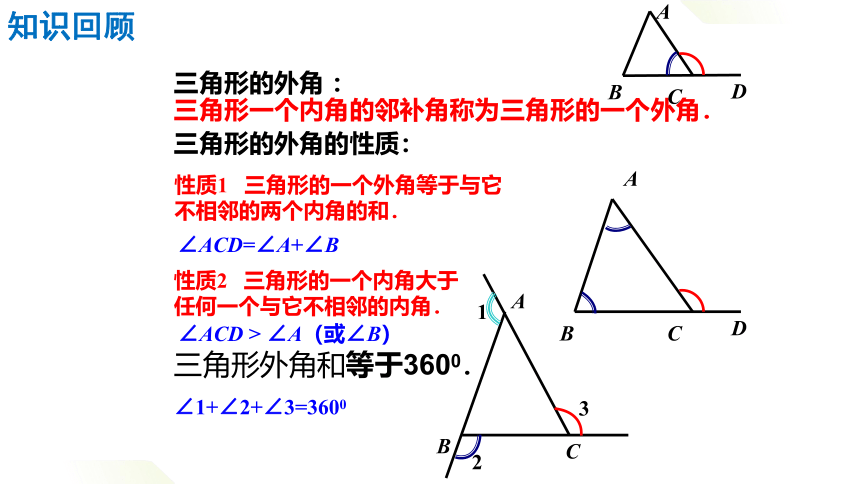
三角形的外角 :
三角形的外角的性质:
三角形外角和等于3600.
三角形一个内角的邻补角称为三角形的一个外角.
性质1 三角形的一个外角等于与它不相邻的两个内角的和.
性质2 三角形的一个内角大于任何一个与它不相邻的内角.
A
D
C
B
∠ACD=∠A+∠B
∠ACD > ∠A(或∠B)
A
C
B
1
2
3
∠1+∠2+∠3=3600
A
D
C
B
例题5 如图,在△ABC中,已知点D是边BC上的一点,
且∠ADE=∠B,那么∠1与∠2相等吗?为什么?
解 因为∠ADC=∠B+∠1(三角形的一个外角等于
与它不相邻的两个内角的和),
即∠ADE+∠2=∠B+∠1
又∠ADE=∠B(已知)
所以∠1=∠2(等式性质)
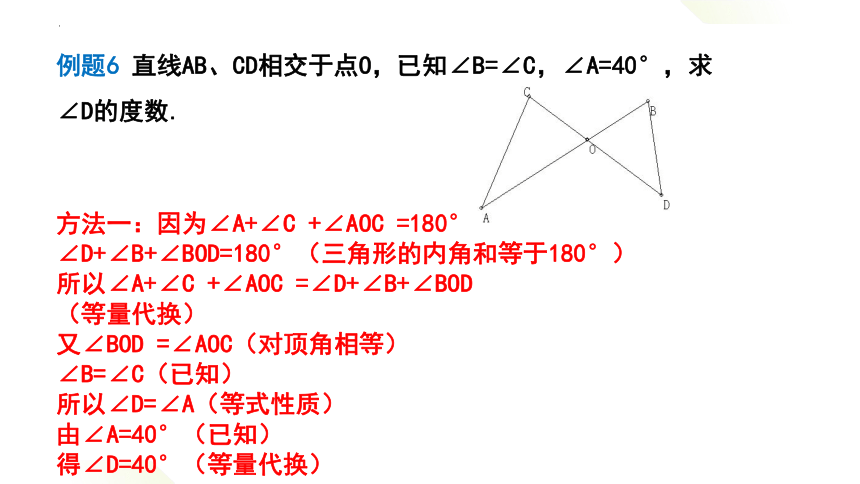
例题6 直线AB、CD相交于点O,已知∠B=∠C,∠A=40°,求∠D的度数.
方法一:因为∠A+∠C +∠AOC =180°
∠D+∠B+∠BOD=180°(三角形的内角和等于180°)
所以∠A+∠C +∠AOC =∠D+∠B+∠BOD
(等量代换)
又∠BOD =∠AOC(对顶角相等)
∠B=∠C(已知)
所以∠D=∠A(等式性质)
由∠A=40°(已知)
得∠D=40°(等量代换)
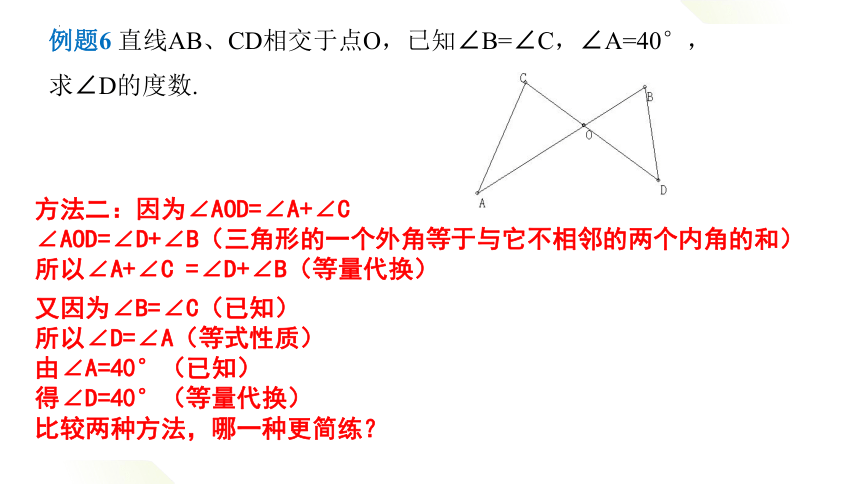
方法二:因为∠AOD=∠A+∠C
∠AOD=∠D+∠B(三角形的一个外角等于与它不相邻的两个内角的和)
所以∠A+∠C =∠D+∠B(等量代换)
又因为∠B=∠C(已知)
所以∠D=∠A(等式性质)
由∠A=40°(已知)
得∠D=40°(等量代换)
比较两种方法,哪一种更简练?
例题6 直线AB、CD相交于点O,已知∠B=∠C,∠A=40°,求∠D的度数.
例题7 如图,∠A+∠B+∠D+∠E+∠F+∠G= _____ 度.
解:如图,连接DG,
则有∠E+∠F+∠EDG+∠FGD=360°,
又∵∠GCD=∠ACB,∠A+∠B+∠ACB=180°,
∠CDG+∠CGD+∠GCD=180°,
∴∠A+∠B=∠CDG+∠CGD,
∴∠A+∠B+∠D+∠E+∠F+∠G=∠E+∠F+∠EDG+∠FGD=360°.
如图中,∠A+∠B+∠C+∠D+∠F+∠G等于 _____ 度.
解:如图,连接CD.
则∠1+∠2=∠G+∠F,
∴∠A+∠B+∠C+∠D+∠F+∠G=
∠A+∠B+∠BCE+∠1+∠2+∠ADE
=(4-2)×180°=360°.
故∠A+∠B+∠C+∠D+∠F+∠G的度数是360°.
故答案为:360.
360
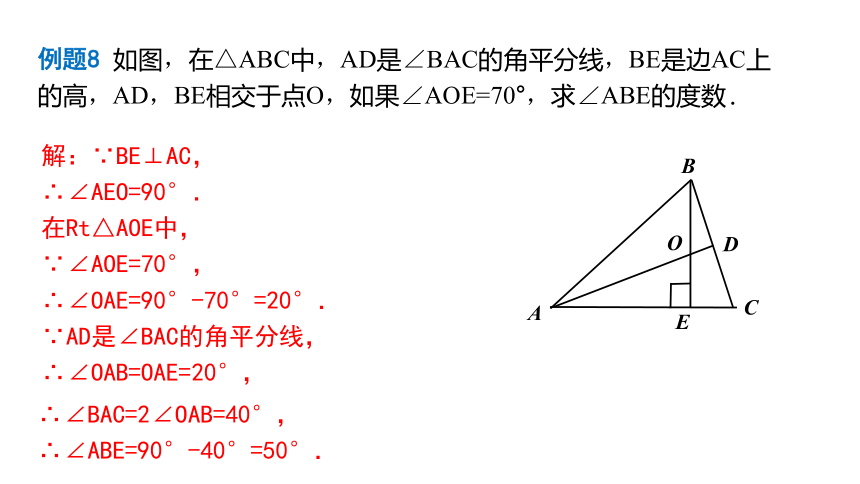
例题8 如图,在△ABC中,AD是∠BAC的角平分线,BE是边AC上的高,AD,BE相交于点O,如果∠AOE=70°,求∠ABE的度数.
解:∵BE⊥AC,
∴∠AEO=90°.
在Rt△AOE中,
∵∠AOE=70°,
∴∠OAE=90°-70°=20°.
∵AD是∠BAC的角平分线,
∴∠OAB=OAE=20°,
O
A
E
C
B
D
∴∠BAC=2∠OAB=40°,
∴∠ABE=90°-40°=50°.
如图,△ABC中,∠B=∠C,点D、E是BC边上的点,且∠C=∠DAE,请说明∠BAE=∠ADE理由.
证明:∵∠C=∠DAE,
∴∠C+∠CAE=∠DAE+∠CAE,
∴∠AEB=∠DAC,
∵∠B=∠C,
∴180°-(∠AEB+∠B)=180°-(∠DAC+∠C),
即∠BAE=∠ADE.
1.如果三角形的一个外角等于与它相邻的内角的2倍,且等于与它不相邻的一个内角的2倍,那么这个三角形一定是( ____ )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
【解析】解:设这个外角的度数为x,则与其相邻的内角为180°-x.
根据题意得,x=2(180°-x),
解得x=120°.
则与其相邻的内角为60°,
D
等于与它不相邻的一个内角的2倍,
可得这个与其不相邻的内角为60°;
即得该三角形为等边三角形.
故选:D.
2.已知△ABC的三个内角∠A,∠B,∠C满足关系式∠B+∠C=2∠A,则此三角形( ____ )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
【解析】解:在△ABC中,∠B+∠C=2∠A,
∴∠A+2∠A=180°,
∴∠A=60°,
故选:B.
B
3.如图,在△ABC中,∠A=x°,∠B=48°,∠C=30°,则x= _____ 度.
【解析】解:在△ABC中,∠A=x°,∠B=48°,∠C=30°,
∴∠A=180°-∠B-∠C,
即x°=180°-48°-30°=102°.
故答案为:102.
102
4.如图,△ABC中,∠A=x°,∠B=37°,外角∠ACD=118°,则x= ____ 度.
【解析】解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD-∠B,
∵∠B=37°,∠ACD=118°,
∴∠A=118°-37°=81°,
∴x=81.
故答案为:81.
81
5.如图,在△ABC中,∠ABC=70°,∠ACB=50°,三个内角的平分线交于点P,则∠APB= _____ 度,∠BPC= _____ 度,延长BP交AC于点Q,则∠APQ= ____ 度,∠AQP= ____ 度.
【解析】解:在△ABC中,∠ABC=70°,∠ACB=50°,
∴∠BAC=180°-∠ABC-∠ACB=180°-70°-50°=60°.
∵三个内角的平分线交于点P,
∴∠ABP=∠CBP= ∠ABC= ×70°=35°,∠BAP=∠PAQ= ∠BAC= ×60°=30°,∠BCP= ∠ACB= ×50°=25°.
115
120
65
85
在△ABP中,∠ABP=35°,∠BAP=30°,
∴∠APB=180°-∠ABP-∠BAP=180°-35°-30°=115°
在△BCP中,∠CBP=35°,∠BCP=25°,
∴∠BPC=180°-∠CBP-∠BCP=180°-35°-25°=120°.
∵∠APQ为△ABP的外角,
∴∠APQ=∠ABP+∠BAP=35°+30°=65°.
在△APQ中,∠APQ=65°,∠PAQ=30°,
∴∠AQP=180°-∠APQ-∠PAQ=180°-65°-30°=85°.
故答案为:115;120;65;85.
6.如图,在△ABC中,AH是BC边上的高,AD是∠BAC的平分线,∠B=38°,∠C=46°,则∠BAC= ____ 度,∠DAH= ____ 度,∠ADH= ____ 度,∠HAC= ____ 度.
【解析】解:∵∠B=38°,∠C=46°,
∴∠BAC=180°-∠B-∠C=180°-38°-46°=96°,
∵AD是∠BAC的平分线,
∴∠DAC= ∠BAC=48°,
∵AH是BC边上的高,
∴∠AHD=∠AHC=90°,
96
4
86
44
∴∠CAH=90°-∠C=44°,
∴∠DAH=∠DAC-∠CAH=48°-44°=4°,
∴∠ADH=90°-∠DAH=86°.
故答案为:96,4,86,44.
7.如图,Rt△ABC中,∠ACB=90°,CD是∠ACB的角平分线,交AB于点D,将AC沿着CD翻折,使A落在BC上A′处,∠A=50°,则∠A′DB= ____ 度.
【解析】解:∵将△ACD沿CD翻折,点A恰好落在BC边上的A′处,
∴∠ACD=∠BCD,∠CDA=∠CDA′,
∵∠ACB=90°,∠A=50°,
∴∠ACD=∠BCD=45°,
∴∠ADC=∠A′DC=85°,
∴∠BDA'=180°-85°-85°=10°.
故答案为:10.
10
8.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= _____ 度.
【解析】解:如图:
___
∵∠1=∠B+∠2,∠2=∠F+∠C,
∴∠1=∠B+∠F+∠C,
∴∠A+∠1+∠D+∠E+∠G=∠A+∠B+∠C+∠F+∠D+∠E+∠G=(5-2)×180°=540°.
故答案为:540.
540
9.如图,求∠A+∠B+∠D+∠F+∠P+∠Q的度数.
【解析】解:在△ABC中,∠A+∠B=180°-∠ACB=180°-∠ECO,
在△DEF中,∠D+∠F=180°-∠DEF=180°-∠CEO,
在△OPQ中,∠P+∠Q=180°-∠POQ=180°-∠COE,
∠A+∠B+∠D+∠F+∠P+∠Q
=180°-∠ECO+180°-∠CEO+180°-∠COE
=540°-(∠ECO+∠CEO+∠COE)
=540°-180°
=360°.
10.如图,AB∥CD,∠E=35°,∠ECD=108°,试求∠EAB的度数.
【解析】解:延长BA交CE于点F,
∵AB∥CD,∠ECD=108°,
∴∠EFA=∠ECD=108°.
∵∠EAB是△AEF的外角,
∴∠EAB=∠E+∠AFE=35°+108°=143°.
谢谢
14.2三角形的内角和性质与外角和性质应用(第3课时)
2023-2024学年沪教版七年级下册数学课件
知识回顾
三角形的外角 :
三角形的外角的性质:
三角形外角和等于3600.
三角形一个内角的邻补角称为三角形的一个外角.
性质1 三角形的一个外角等于与它不相邻的两个内角的和.
性质2 三角形的一个内角大于任何一个与它不相邻的内角.
A
D
C
B
∠ACD=∠A+∠B
∠ACD > ∠A(或∠B)
A
C
B
1
2
3
∠1+∠2+∠3=3600
A
D
C
B
例题5 如图,在△ABC中,已知点D是边BC上的一点,
且∠ADE=∠B,那么∠1与∠2相等吗?为什么?
解 因为∠ADC=∠B+∠1(三角形的一个外角等于
与它不相邻的两个内角的和),
即∠ADE+∠2=∠B+∠1
又∠ADE=∠B(已知)
所以∠1=∠2(等式性质)
例题6 直线AB、CD相交于点O,已知∠B=∠C,∠A=40°,求∠D的度数.
方法一:因为∠A+∠C +∠AOC =180°
∠D+∠B+∠BOD=180°(三角形的内角和等于180°)
所以∠A+∠C +∠AOC =∠D+∠B+∠BOD
(等量代换)
又∠BOD =∠AOC(对顶角相等)
∠B=∠C(已知)
所以∠D=∠A(等式性质)
由∠A=40°(已知)
得∠D=40°(等量代换)
方法二:因为∠AOD=∠A+∠C
∠AOD=∠D+∠B(三角形的一个外角等于与它不相邻的两个内角的和)
所以∠A+∠C =∠D+∠B(等量代换)
又因为∠B=∠C(已知)
所以∠D=∠A(等式性质)
由∠A=40°(已知)
得∠D=40°(等量代换)
比较两种方法,哪一种更简练?
例题6 直线AB、CD相交于点O,已知∠B=∠C,∠A=40°,求∠D的度数.
例题7 如图,∠A+∠B+∠D+∠E+∠F+∠G= _____ 度.
解:如图,连接DG,
则有∠E+∠F+∠EDG+∠FGD=360°,
又∵∠GCD=∠ACB,∠A+∠B+∠ACB=180°,
∠CDG+∠CGD+∠GCD=180°,
∴∠A+∠B=∠CDG+∠CGD,
∴∠A+∠B+∠D+∠E+∠F+∠G=∠E+∠F+∠EDG+∠FGD=360°.
如图中,∠A+∠B+∠C+∠D+∠F+∠G等于 _____ 度.
解:如图,连接CD.
则∠1+∠2=∠G+∠F,
∴∠A+∠B+∠C+∠D+∠F+∠G=
∠A+∠B+∠BCE+∠1+∠2+∠ADE
=(4-2)×180°=360°.
故∠A+∠B+∠C+∠D+∠F+∠G的度数是360°.
故答案为:360.
360
例题8 如图,在△ABC中,AD是∠BAC的角平分线,BE是边AC上的高,AD,BE相交于点O,如果∠AOE=70°,求∠ABE的度数.
解:∵BE⊥AC,
∴∠AEO=90°.
在Rt△AOE中,
∵∠AOE=70°,
∴∠OAE=90°-70°=20°.
∵AD是∠BAC的角平分线,
∴∠OAB=OAE=20°,
O
A
E
C
B
D
∴∠BAC=2∠OAB=40°,
∴∠ABE=90°-40°=50°.
如图,△ABC中,∠B=∠C,点D、E是BC边上的点,且∠C=∠DAE,请说明∠BAE=∠ADE理由.
证明:∵∠C=∠DAE,
∴∠C+∠CAE=∠DAE+∠CAE,
∴∠AEB=∠DAC,
∵∠B=∠C,
∴180°-(∠AEB+∠B)=180°-(∠DAC+∠C),
即∠BAE=∠ADE.
1.如果三角形的一个外角等于与它相邻的内角的2倍,且等于与它不相邻的一个内角的2倍,那么这个三角形一定是( ____ )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
【解析】解:设这个外角的度数为x,则与其相邻的内角为180°-x.
根据题意得,x=2(180°-x),
解得x=120°.
则与其相邻的内角为60°,
D
等于与它不相邻的一个内角的2倍,
可得这个与其不相邻的内角为60°;
即得该三角形为等边三角形.
故选:D.
2.已知△ABC的三个内角∠A,∠B,∠C满足关系式∠B+∠C=2∠A,则此三角形( ____ )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
【解析】解:在△ABC中,∠B+∠C=2∠A,
∴∠A+2∠A=180°,
∴∠A=60°,
故选:B.
B
3.如图,在△ABC中,∠A=x°,∠B=48°,∠C=30°,则x= _____ 度.
【解析】解:在△ABC中,∠A=x°,∠B=48°,∠C=30°,
∴∠A=180°-∠B-∠C,
即x°=180°-48°-30°=102°.
故答案为:102.
102
4.如图,△ABC中,∠A=x°,∠B=37°,外角∠ACD=118°,则x= ____ 度.
【解析】解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD-∠B,
∵∠B=37°,∠ACD=118°,
∴∠A=118°-37°=81°,
∴x=81.
故答案为:81.
81
5.如图,在△ABC中,∠ABC=70°,∠ACB=50°,三个内角的平分线交于点P,则∠APB= _____ 度,∠BPC= _____ 度,延长BP交AC于点Q,则∠APQ= ____ 度,∠AQP= ____ 度.
【解析】解:在△ABC中,∠ABC=70°,∠ACB=50°,
∴∠BAC=180°-∠ABC-∠ACB=180°-70°-50°=60°.
∵三个内角的平分线交于点P,
∴∠ABP=∠CBP= ∠ABC= ×70°=35°,∠BAP=∠PAQ= ∠BAC= ×60°=30°,∠BCP= ∠ACB= ×50°=25°.
115
120
65
85
在△ABP中,∠ABP=35°,∠BAP=30°,
∴∠APB=180°-∠ABP-∠BAP=180°-35°-30°=115°
在△BCP中,∠CBP=35°,∠BCP=25°,
∴∠BPC=180°-∠CBP-∠BCP=180°-35°-25°=120°.
∵∠APQ为△ABP的外角,
∴∠APQ=∠ABP+∠BAP=35°+30°=65°.
在△APQ中,∠APQ=65°,∠PAQ=30°,
∴∠AQP=180°-∠APQ-∠PAQ=180°-65°-30°=85°.
故答案为:115;120;65;85.
6.如图,在△ABC中,AH是BC边上的高,AD是∠BAC的平分线,∠B=38°,∠C=46°,则∠BAC= ____ 度,∠DAH= ____ 度,∠ADH= ____ 度,∠HAC= ____ 度.
【解析】解:∵∠B=38°,∠C=46°,
∴∠BAC=180°-∠B-∠C=180°-38°-46°=96°,
∵AD是∠BAC的平分线,
∴∠DAC= ∠BAC=48°,
∵AH是BC边上的高,
∴∠AHD=∠AHC=90°,
96
4
86
44
∴∠CAH=90°-∠C=44°,
∴∠DAH=∠DAC-∠CAH=48°-44°=4°,
∴∠ADH=90°-∠DAH=86°.
故答案为:96,4,86,44.
7.如图,Rt△ABC中,∠ACB=90°,CD是∠ACB的角平分线,交AB于点D,将AC沿着CD翻折,使A落在BC上A′处,∠A=50°,则∠A′DB= ____ 度.
【解析】解:∵将△ACD沿CD翻折,点A恰好落在BC边上的A′处,
∴∠ACD=∠BCD,∠CDA=∠CDA′,
∵∠ACB=90°,∠A=50°,
∴∠ACD=∠BCD=45°,
∴∠ADC=∠A′DC=85°,
∴∠BDA'=180°-85°-85°=10°.
故答案为:10.
10
8.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= _____ 度.
【解析】解:如图:
___
∵∠1=∠B+∠2,∠2=∠F+∠C,
∴∠1=∠B+∠F+∠C,
∴∠A+∠1+∠D+∠E+∠G=∠A+∠B+∠C+∠F+∠D+∠E+∠G=(5-2)×180°=540°.
故答案为:540.
540
9.如图,求∠A+∠B+∠D+∠F+∠P+∠Q的度数.
【解析】解:在△ABC中,∠A+∠B=180°-∠ACB=180°-∠ECO,
在△DEF中,∠D+∠F=180°-∠DEF=180°-∠CEO,
在△OPQ中,∠P+∠Q=180°-∠POQ=180°-∠COE,
∠A+∠B+∠D+∠F+∠P+∠Q
=180°-∠ECO+180°-∠CEO+180°-∠COE
=540°-(∠ECO+∠CEO+∠COE)
=540°-180°
=360°.
10.如图,AB∥CD,∠E=35°,∠ECD=108°,试求∠EAB的度数.
【解析】解:延长BA交CE于点F,
∵AB∥CD,∠ECD=108°,
∴∠EFA=∠ECD=108°.
∵∠EAB是△AEF的外角,
∴∠EAB=∠E+∠AFE=35°+108°=143°.
谢谢
