14.2三角形的外角与外角和(第2课时) 课件(共36张PPT)
文档属性
| 名称 | 14.2三角形的外角与外角和(第2课时) 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览

文档简介
(共36张PPT)
14.2三角形的外角与外角和(第2课时)
2023-2024学年沪教版七年级下册数学课件
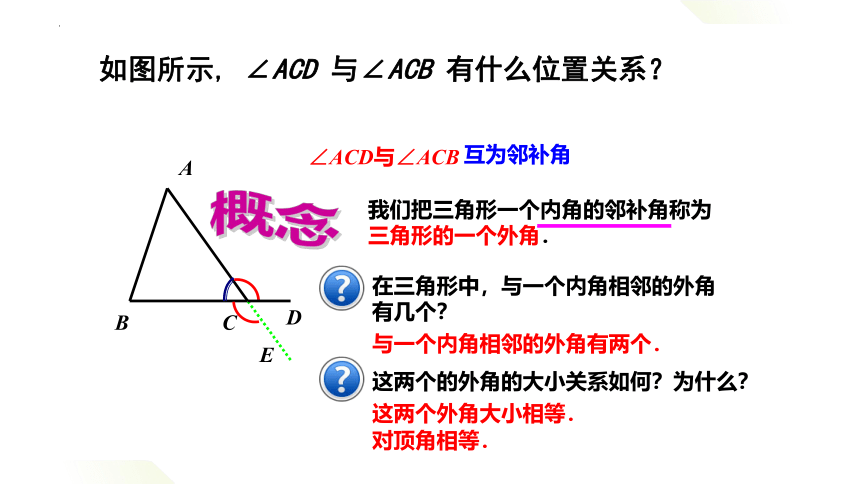
如图所示, ∠ACD 与∠ACB 有什么位置关系?
A
D
C
B
∠ACD与∠ACB
互为邻补角
我们把三角形一个内角的邻补角称为
三角形的一个外角.
概念
在三角形中,与一个内角相邻的外角
有几个?
E
与一个内角相邻的外角有两个.
这两个的外角的大小关系如何?为什么?
这两个外角大小相等.
对顶角相等.
A
B
C
D
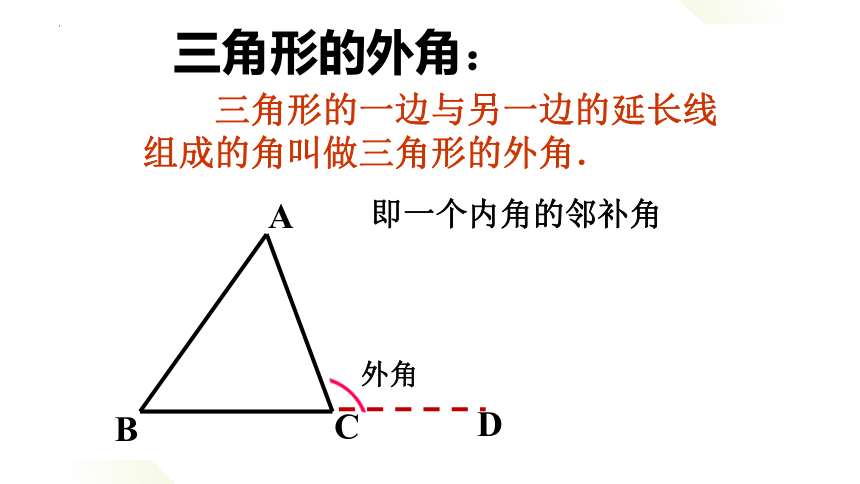
三角形的外角:
三角形的一边与另一边的延长线组成的角叫做三角形的外角.
外角
即一个内角的邻补角
探究新知
A
D
C
B
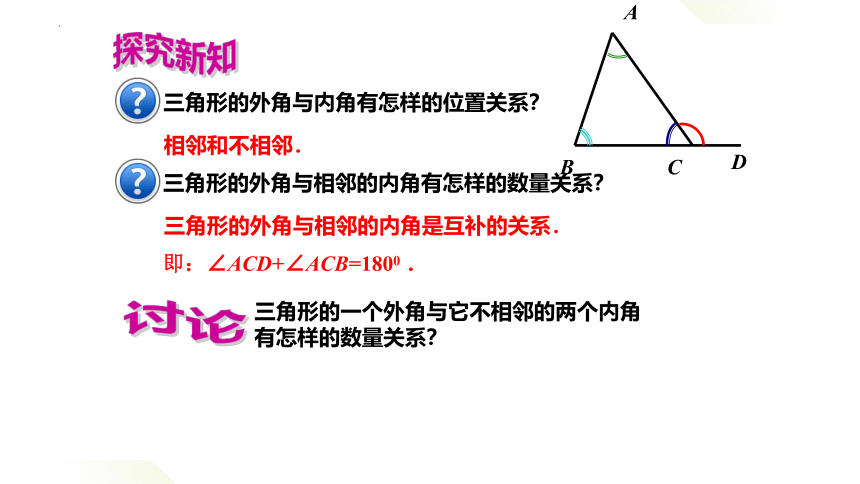
三角形的外角与内角有怎样的位置关系?
相邻和不相邻.
三角形的外角与相邻的内角有怎样的数量关系?
三角形的外角与相邻的内角是互补的关系.
即:∠ACD+∠ACB=1800 .
讨论
三角形的一个外角与它不相邻的两个内角
有怎样的数量关系?
探究新知
A
D
C
B
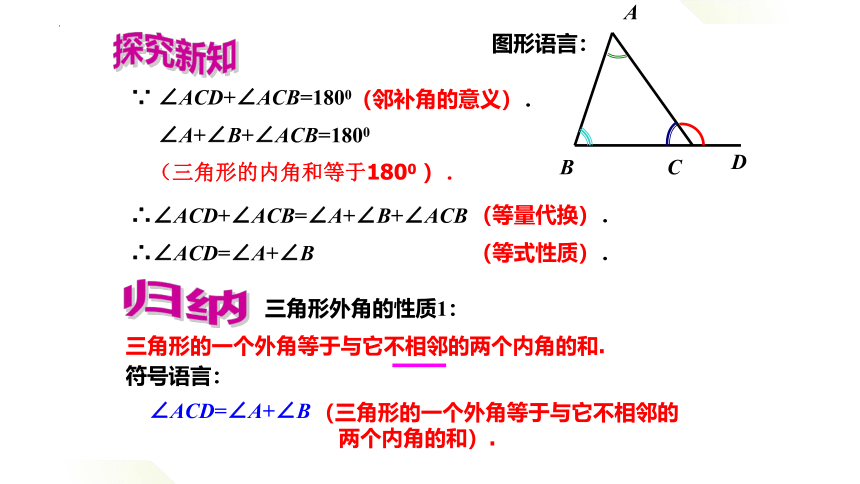
∵ ∠ACD+∠ACB=1800
(邻补角的意义).
∠A+∠B+∠ACB=1800
(三角形的内角和等于1800 ).
∴∠ACD+∠ACB=∠A+∠B+∠ACB
(等量代换).
∴∠ACD=∠A+∠B
(等式性质).
归纳
三角形外角的性质1:
三角形的一个外角等于与它不相邻的两个内角的和.
符号语言:
(三角形的一个外角等于与它不相邻的
两个内角的和).
∠ACD=∠A+∠B
图形语言:
探究新知
A
D
C
B
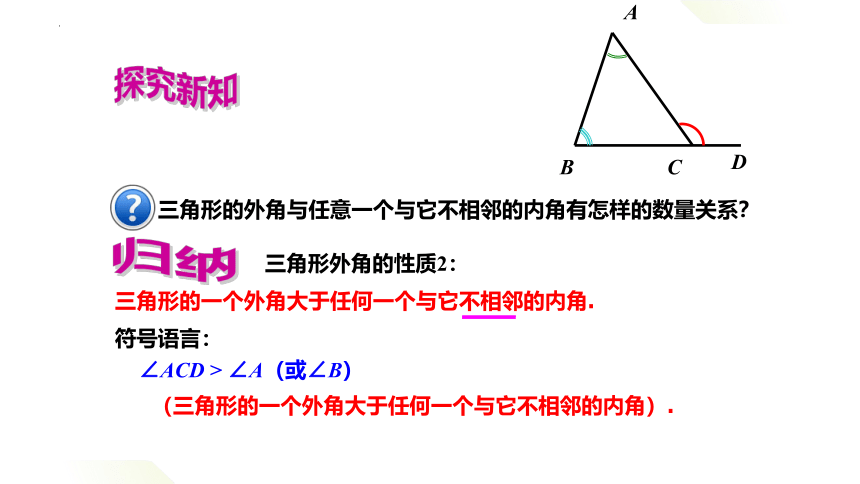
三角形外角的性质2:
三角形的一个外角大于任何一个与它不相邻的内角.
符号语言:
∠ACD > ∠A(或∠B)
三角形的外角与任意一个与它不相邻的内角有怎样的数量关系?
归纳
(三角形的一个外角大于任何一个与它不相邻的内角).
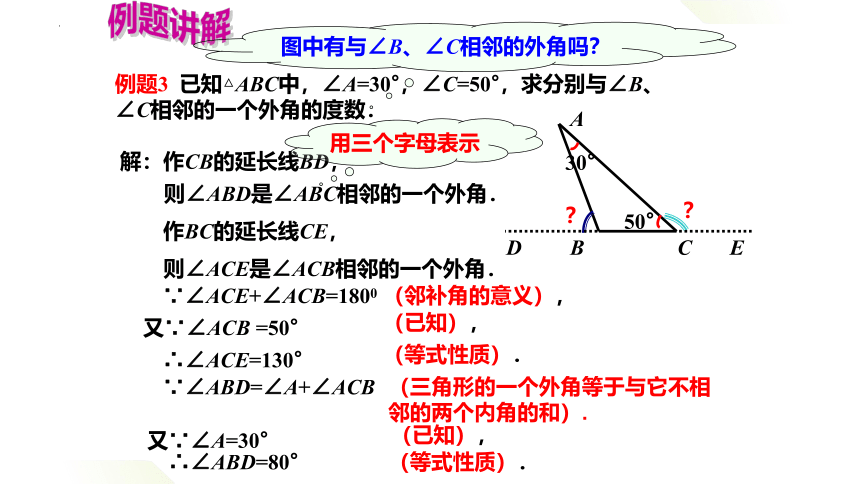
例题3 已知△ABC中,∠A=30°,∠C=50°,求分别与∠B、∠C相邻的一个外角的度数.
例题讲解
A
D
C
B
图中有与∠B、∠C相邻的外角吗?
解:作CB的延长线BD,
则∠ABD是∠ABC相邻的一个外角.
50°
30°
?
用三个字母表示
∵∠ABD=∠A+∠ACB
(三角形的一个外角等于与它不相邻的两个内角的和).
又∵∠ACB =50°
(已知),
∴∠ABD=80°
作BC的延长线CE,
E
则∠ACE是∠ACB相邻的一个外角.
?
∵∠ACE+∠ACB=1800
(邻补角的意义),
∴∠ACE=130°
(等式性质).
又∵∠A=30°
(已知),
(等式性质).
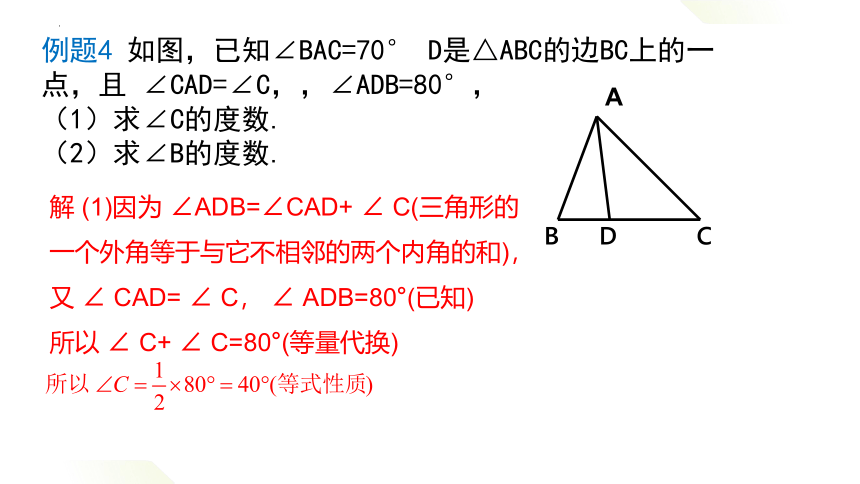
例题4 如图,已知∠BAC=70° D是△ABC的边BC上的一点,且 ∠CAD=∠C,,∠ADB=80°,
(1)求∠C的度数.
(2)求∠B的度数.
A
B
D
C
解 (1)因为 ∠ADB=∠CAD+ ∠ C(三角形的一个外角等于与它不相邻的两个内角的和),又 ∠ CAD= ∠ C, ∠ ADB=80°(已知)
所以 ∠ C+ ∠ C=80°(等量代换)
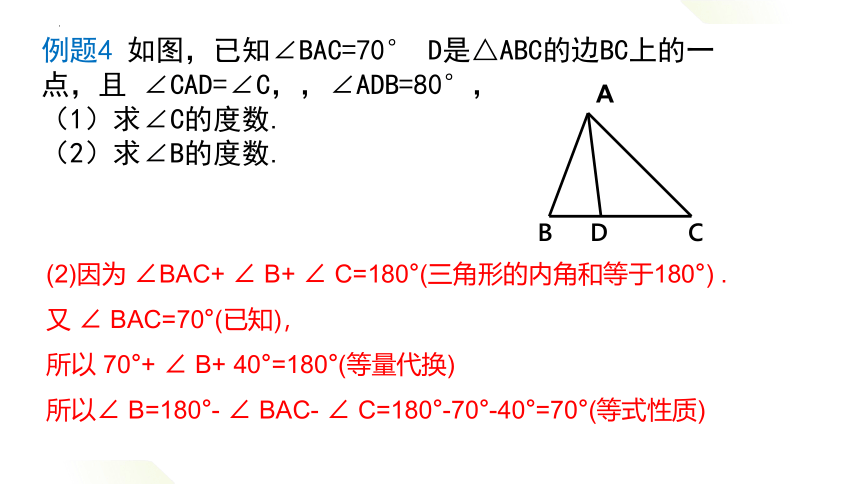
(2)因为 ∠BAC+ ∠ B+ ∠ C=180°(三角形的内角和等于180°) .
又 ∠ BAC=70°(已知),
所以 70°+ ∠ B+ 40°=180°(等量代换)
所以∠ B=180°- ∠ BAC- ∠ C=180°-70°-40°=70°(等式性质)
例题4 如图,已知∠BAC=70° D是△ABC的边BC上的一点,且 ∠CAD=∠C,,∠ADB=80°,
(1)求∠C的度数.
(2)求∠B的度数.
A
B
D
C
A
B
C
6
1
2
3
4
5
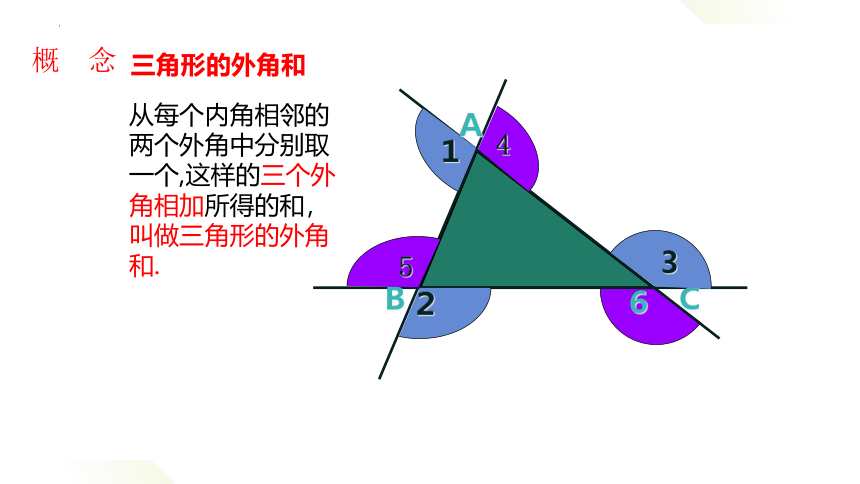
三角形的外角和
从每个内角相邻的两个外角中分别取一个,这样的三个外角相加所得的和,叫做三角形的外角和.
概 念
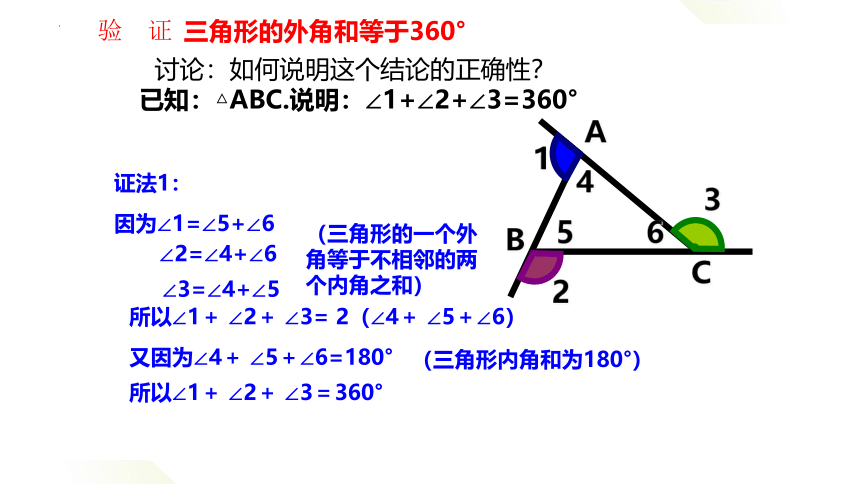
∠2=∠4+∠6
∠3=∠4+∠5
(三角形的一个外角等于不相邻的两个内角之和)
所以∠1+ ∠2+ ∠3= 2(∠4+ ∠5+∠6)
又因为∠4+ ∠5+∠6=180°
所以∠1+ ∠2+ ∠3=360°
因为∠1=∠5+∠6
证法1:
A
B
C
1
2
3
(三角形内角和为180°)
三角形的外角和等于360°
讨论:如何说明这个结论的正确性?
已知:△ABC.说明:∠1+∠2+∠3=360°
4
5
6
验 证
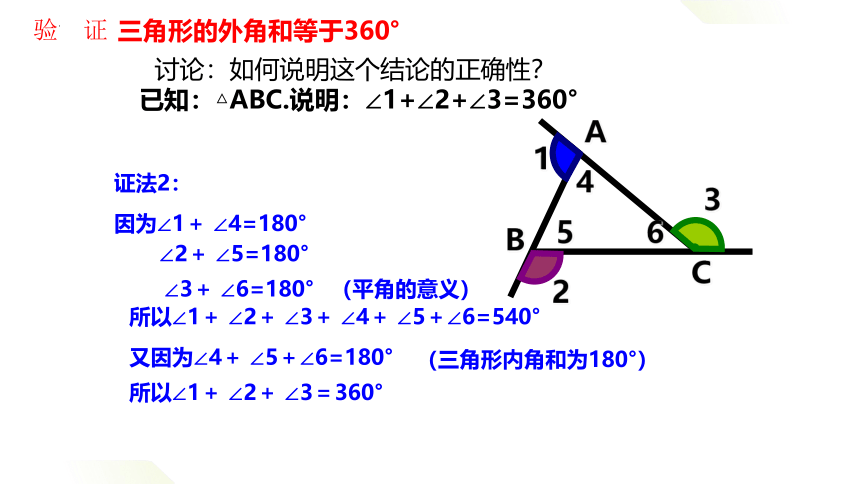
∠2+ ∠5=180°
∠3+ ∠6=180°
(平角的意义)
所以∠1+ ∠2+ ∠3+ ∠4+ ∠5+∠6=540°
又因为∠4+ ∠5+∠6=180°
所以∠1+ ∠2+ ∠3=360°
因为∠1+ ∠4=180°
证法2:
A
B
C
1
2
3
(三角形内角和为180°)
三角形的外角和等于360°
讨论:如何说明这个结论的正确性?
已知:△ABC.说明:∠1+∠2+∠3=360°
4
5
6
验 证
1.如果三角形的一个外角小于和它相邻的内角,那么这个三角形为( ____ )
A.钝角三角形
B.锐角三角形
C.直角三角形
D.以上都不对
【解析】解:∵三角形的一个外角小于和它相邻的内角,
∴该外角小于90度,与它相邻的内角大于90度,
∴这个三角形为钝角三角形.
故选:A.
A
2.下列说法错误的有( ____ )
①三角形任何两边之和大于第三边
②三角形的一个外角大于任何一个内角
③三角形的任何两边之差小于第三边
④三角形的任一内角都小于它的外角
A.1个
B.2个
C.3个
D.4个
【解析】解:①三角形任何两边之和大于第三边,正确,故①
B
不符合题意;
②三角形的一个外角不一定大于任何一个内角,故②符合题意;
③三角形的任何两边之差小于第三边,正确,故③不符合题意;
④三角形的任一内角不一定小于它的外角,故④符合题意.
∴错误的是②④,
故选:B.
3.如图,在△ABC中,∠BAC=80°,∠B=30°,AD平分∠BAC,则∠ADC的度数为( ____ )
A.90°
B.95°
C.70°
D.50°
【解析】解:∵AD平分∠BAC,
∴∠BAD= ∠BAC= ×80°=40°,
又∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=30°+40°=70°.
C
故选:C.
4.如图,已知在△ABC中,∠A=90°,∠1+∠2的度数是( ____ )
A.180°
B.270°
C.360°
D.无法确定
【解析】解:在△ABC中,∠A=90°,
所以∠ACB+∠ABC=90°,
又因为∠1+∠ACB=180°,
∠2+∠ABC=180°,
B
所以∠1+∠2=270°,
故选:B.
5.如图,一副三角板,如图所示叠放在一起,则图中∠α的度数是( ____ )
A.55°
B.65°
C.75°
D.85°
【解析】解:如图,∵∠1=60°,∠2=45°,
∴∠α=180°-45°-60°=75°,
故选:C.
C
6.如果三角形的一个内角等于它的外角,那么这个三角形是 _____ 三角形.
【解析】解:不妨设∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
故答案为:直角.
直角
7.在△ABC中,∠A=35°,∠B的外角等于105°,那么∠C= _____ .
【解析】解:∵∠A+∠C=105°,∠A=35°,
∴∠C=105°-35°=70°.
故答案为:70°.
70°
8.如果等腰三角形的一个外角是30°,那么它的底角是 ____ 度;如果等腰三角形的一个外角是110°,那么它的底角是度 ____________ .
【解析】解:∵等腰三角形的一个外角为30°,
∴相邻角为180°-30°=150°,
∵三角形的底角不能为钝角,
∴150°角为顶角,
∴底角为:(180°-150°)÷2=15°;
∵等腰三角形的一个外角是110°,
∴与这个外角相邻的内角是180°-110°=70°,
①70°角是顶角时,它的底角为: (180°-70°)=55°,
15
55°或70°
②70°角是底角时,它的底角70°,
所以,它的底角是55°或70°.
故答案为:15°;55°或70°.
9.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D= _____ .
【解析】解:∵∠B=46°,∠C=30°,
∴∠DAC=∠B+∠C=76°,
∵∠EFC=70°,
∴∠AFD=70°,
∴∠D=180°-∠DAC-∠AFD=34°,
故答案为:34°.
34°
10.已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC,AD与BC的位置有何关系?并说明理由.___
【解析】解:AD∥BC.
∵∠EAC=∠B+∠C,∠B=∠C,
∴∠EAC=2∠B.
又∵AD平分外角∠EAC,
∴∠EAC=2∠EAD,
∴∠B=∠EAD,
∴AD∥BC.
11.如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
分析:连接AD并延长至点E,
要求∠BDC的度数,只需求∠BDE+∠CDE即可,
解:∵∠BDE=∠B+ ______ ,
∠CDE=∠C+ ______ ,
∵∠BDC=∠BDE+∠CDE,
∴∠BDC=∠B+ ______ +∠C+ ______ .
∵∠BAC=51°,∠B=20°,∠C=30°,
∴∠BDC= ______ .
∠BAD
∠CAD
∠BAD
∠CAD
101°
【解析】解:∵∠BDE=∠B+∠BAD,
∠CDE=∠C+∠CAD,
∵∠BDC=∠BDE+∠CDE,
∴∠BDC=∠B+∠BAD+∠C+∠CAD.
∵∠BAC=51°,∠B=20°,∠C=30°,
∴∠BDC=101°.
故答案为:∠BAD,∠CAD,∠BAD,∠CAD,101°.
12.某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC= ______ ;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并说明理由.
(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC= _____ °,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R= ____ °.
122°
119
29
_________
【解析】解:(1)∵PB、PC分别平分∠ABC和∠ACB,
∴∠PBC= ABC,∠PCB= ∠ACB(角平分线的定义),
∵∠BPC+∠PBC+∠PCB=180°(三角形内角和定理),
∴∠BPC=180°-(∠PBC+∠PCB)
=180°-( ∠ABC+ ∠ACB)=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=180°-90°+ ∠A
=90°+ ∠A
=90
=122°.
故答案为:122°;
(2)∵BE是∠ABD的平分线,CE是∠ACB的平分线,
∴∠ECB= ∠ACB,∠EBD= ∠ABD.
∵∠ABD是△ABC的外角,∠EBD是△BCE的外角,
∴∠ABD=∠A+∠ACB,∠EBD=∠ECB+∠BEC,
∴∠EBD= ∠ABD= (∠A+∠ACB)=∠BEC+∠ECB,即 ∠A+∠ECB=∠ECB+∠BEC,
∴∠BEC= ∠A= ;
_________
(3)结论:∠BQC=90°- ∠A.
理由如下:∵∠CBM与∠BCN是△ABC的外角,
∴∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,
∵BQ,CQ分别是∠ABC与∠ACB外角的平分线,
∴∠QBC= (∠A+∠ACB),∠QCB= (∠A+∠ABC).
∵∠QBC+∠QCB+∠BQC=180°,
∴∠BQC=180°-∠QBC-∠QCB,
=180°- (∠A+∠ACB)- (∠A+∠ABC),
=180°- ∠A- (∠A+∠ABC+∠ACB),
=180°- ∠A-90°
=90°- ∠A;
(4)由(3)可知,∠BQC=90°- ∠A=90°- =58°,
由(1)可知∠BPC=90°+ ∠BQC=90°+ =119°;
由(2)可知,∠R= ∠BQC=29°
故答案为119,29.
谢谢
14.2三角形的外角与外角和(第2课时)
2023-2024学年沪教版七年级下册数学课件
如图所示, ∠ACD 与∠ACB 有什么位置关系?
A
D
C
B
∠ACD与∠ACB
互为邻补角
我们把三角形一个内角的邻补角称为
三角形的一个外角.
概念
在三角形中,与一个内角相邻的外角
有几个?
E
与一个内角相邻的外角有两个.
这两个的外角的大小关系如何?为什么?
这两个外角大小相等.
对顶角相等.
A
B
C
D
三角形的外角:
三角形的一边与另一边的延长线组成的角叫做三角形的外角.
外角
即一个内角的邻补角
探究新知
A
D
C
B
三角形的外角与内角有怎样的位置关系?
相邻和不相邻.
三角形的外角与相邻的内角有怎样的数量关系?
三角形的外角与相邻的内角是互补的关系.
即:∠ACD+∠ACB=1800 .
讨论
三角形的一个外角与它不相邻的两个内角
有怎样的数量关系?
探究新知
A
D
C
B
∵ ∠ACD+∠ACB=1800
(邻补角的意义).
∠A+∠B+∠ACB=1800
(三角形的内角和等于1800 ).
∴∠ACD+∠ACB=∠A+∠B+∠ACB
(等量代换).
∴∠ACD=∠A+∠B
(等式性质).
归纳
三角形外角的性质1:
三角形的一个外角等于与它不相邻的两个内角的和.
符号语言:
(三角形的一个外角等于与它不相邻的
两个内角的和).
∠ACD=∠A+∠B
图形语言:
探究新知
A
D
C
B
三角形外角的性质2:
三角形的一个外角大于任何一个与它不相邻的内角.
符号语言:
∠ACD > ∠A(或∠B)
三角形的外角与任意一个与它不相邻的内角有怎样的数量关系?
归纳
(三角形的一个外角大于任何一个与它不相邻的内角).
例题3 已知△ABC中,∠A=30°,∠C=50°,求分别与∠B、∠C相邻的一个外角的度数.
例题讲解
A
D
C
B
图中有与∠B、∠C相邻的外角吗?
解:作CB的延长线BD,
则∠ABD是∠ABC相邻的一个外角.
50°
30°
?
用三个字母表示
∵∠ABD=∠A+∠ACB
(三角形的一个外角等于与它不相邻的两个内角的和).
又∵∠ACB =50°
(已知),
∴∠ABD=80°
作BC的延长线CE,
E
则∠ACE是∠ACB相邻的一个外角.
?
∵∠ACE+∠ACB=1800
(邻补角的意义),
∴∠ACE=130°
(等式性质).
又∵∠A=30°
(已知),
(等式性质).
例题4 如图,已知∠BAC=70° D是△ABC的边BC上的一点,且 ∠CAD=∠C,,∠ADB=80°,
(1)求∠C的度数.
(2)求∠B的度数.
A
B
D
C
解 (1)因为 ∠ADB=∠CAD+ ∠ C(三角形的一个外角等于与它不相邻的两个内角的和),又 ∠ CAD= ∠ C, ∠ ADB=80°(已知)
所以 ∠ C+ ∠ C=80°(等量代换)
(2)因为 ∠BAC+ ∠ B+ ∠ C=180°(三角形的内角和等于180°) .
又 ∠ BAC=70°(已知),
所以 70°+ ∠ B+ 40°=180°(等量代换)
所以∠ B=180°- ∠ BAC- ∠ C=180°-70°-40°=70°(等式性质)
例题4 如图,已知∠BAC=70° D是△ABC的边BC上的一点,且 ∠CAD=∠C,,∠ADB=80°,
(1)求∠C的度数.
(2)求∠B的度数.
A
B
D
C
A
B
C
6
1
2
3
4
5
三角形的外角和
从每个内角相邻的两个外角中分别取一个,这样的三个外角相加所得的和,叫做三角形的外角和.
概 念
∠2=∠4+∠6
∠3=∠4+∠5
(三角形的一个外角等于不相邻的两个内角之和)
所以∠1+ ∠2+ ∠3= 2(∠4+ ∠5+∠6)
又因为∠4+ ∠5+∠6=180°
所以∠1+ ∠2+ ∠3=360°
因为∠1=∠5+∠6
证法1:
A
B
C
1
2
3
(三角形内角和为180°)
三角形的外角和等于360°
讨论:如何说明这个结论的正确性?
已知:△ABC.说明:∠1+∠2+∠3=360°
4
5
6
验 证
∠2+ ∠5=180°
∠3+ ∠6=180°
(平角的意义)
所以∠1+ ∠2+ ∠3+ ∠4+ ∠5+∠6=540°
又因为∠4+ ∠5+∠6=180°
所以∠1+ ∠2+ ∠3=360°
因为∠1+ ∠4=180°
证法2:
A
B
C
1
2
3
(三角形内角和为180°)
三角形的外角和等于360°
讨论:如何说明这个结论的正确性?
已知:△ABC.说明:∠1+∠2+∠3=360°
4
5
6
验 证
1.如果三角形的一个外角小于和它相邻的内角,那么这个三角形为( ____ )
A.钝角三角形
B.锐角三角形
C.直角三角形
D.以上都不对
【解析】解:∵三角形的一个外角小于和它相邻的内角,
∴该外角小于90度,与它相邻的内角大于90度,
∴这个三角形为钝角三角形.
故选:A.
A
2.下列说法错误的有( ____ )
①三角形任何两边之和大于第三边
②三角形的一个外角大于任何一个内角
③三角形的任何两边之差小于第三边
④三角形的任一内角都小于它的外角
A.1个
B.2个
C.3个
D.4个
【解析】解:①三角形任何两边之和大于第三边,正确,故①
B
不符合题意;
②三角形的一个外角不一定大于任何一个内角,故②符合题意;
③三角形的任何两边之差小于第三边,正确,故③不符合题意;
④三角形的任一内角不一定小于它的外角,故④符合题意.
∴错误的是②④,
故选:B.
3.如图,在△ABC中,∠BAC=80°,∠B=30°,AD平分∠BAC,则∠ADC的度数为( ____ )
A.90°
B.95°
C.70°
D.50°
【解析】解:∵AD平分∠BAC,
∴∠BAD= ∠BAC= ×80°=40°,
又∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=30°+40°=70°.
C
故选:C.
4.如图,已知在△ABC中,∠A=90°,∠1+∠2的度数是( ____ )
A.180°
B.270°
C.360°
D.无法确定
【解析】解:在△ABC中,∠A=90°,
所以∠ACB+∠ABC=90°,
又因为∠1+∠ACB=180°,
∠2+∠ABC=180°,
B
所以∠1+∠2=270°,
故选:B.
5.如图,一副三角板,如图所示叠放在一起,则图中∠α的度数是( ____ )
A.55°
B.65°
C.75°
D.85°
【解析】解:如图,∵∠1=60°,∠2=45°,
∴∠α=180°-45°-60°=75°,
故选:C.
C
6.如果三角形的一个内角等于它的外角,那么这个三角形是 _____ 三角形.
【解析】解:不妨设∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
故答案为:直角.
直角
7.在△ABC中,∠A=35°,∠B的外角等于105°,那么∠C= _____ .
【解析】解:∵∠A+∠C=105°,∠A=35°,
∴∠C=105°-35°=70°.
故答案为:70°.
70°
8.如果等腰三角形的一个外角是30°,那么它的底角是 ____ 度;如果等腰三角形的一个外角是110°,那么它的底角是度 ____________ .
【解析】解:∵等腰三角形的一个外角为30°,
∴相邻角为180°-30°=150°,
∵三角形的底角不能为钝角,
∴150°角为顶角,
∴底角为:(180°-150°)÷2=15°;
∵等腰三角形的一个外角是110°,
∴与这个外角相邻的内角是180°-110°=70°,
①70°角是顶角时,它的底角为: (180°-70°)=55°,
15
55°或70°
②70°角是底角时,它的底角70°,
所以,它的底角是55°或70°.
故答案为:15°;55°或70°.
9.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D= _____ .
【解析】解:∵∠B=46°,∠C=30°,
∴∠DAC=∠B+∠C=76°,
∵∠EFC=70°,
∴∠AFD=70°,
∴∠D=180°-∠DAC-∠AFD=34°,
故答案为:34°.
34°
10.已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC,AD与BC的位置有何关系?并说明理由.___
【解析】解:AD∥BC.
∵∠EAC=∠B+∠C,∠B=∠C,
∴∠EAC=2∠B.
又∵AD平分外角∠EAC,
∴∠EAC=2∠EAD,
∴∠B=∠EAD,
∴AD∥BC.
11.如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
分析:连接AD并延长至点E,
要求∠BDC的度数,只需求∠BDE+∠CDE即可,
解:∵∠BDE=∠B+ ______ ,
∠CDE=∠C+ ______ ,
∵∠BDC=∠BDE+∠CDE,
∴∠BDC=∠B+ ______ +∠C+ ______ .
∵∠BAC=51°,∠B=20°,∠C=30°,
∴∠BDC= ______ .
∠BAD
∠CAD
∠BAD
∠CAD
101°
【解析】解:∵∠BDE=∠B+∠BAD,
∠CDE=∠C+∠CAD,
∵∠BDC=∠BDE+∠CDE,
∴∠BDC=∠B+∠BAD+∠C+∠CAD.
∵∠BAC=51°,∠B=20°,∠C=30°,
∴∠BDC=101°.
故答案为:∠BAD,∠CAD,∠BAD,∠CAD,101°.
12.某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC= ______ ;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并说明理由.
(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC= _____ °,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R= ____ °.
122°
119
29
_________
【解析】解:(1)∵PB、PC分别平分∠ABC和∠ACB,
∴∠PBC= ABC,∠PCB= ∠ACB(角平分线的定义),
∵∠BPC+∠PBC+∠PCB=180°(三角形内角和定理),
∴∠BPC=180°-(∠PBC+∠PCB)
=180°-( ∠ABC+ ∠ACB)=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=180°-90°+ ∠A
=90°+ ∠A
=90
=122°.
故答案为:122°;
(2)∵BE是∠ABD的平分线,CE是∠ACB的平分线,
∴∠ECB= ∠ACB,∠EBD= ∠ABD.
∵∠ABD是△ABC的外角,∠EBD是△BCE的外角,
∴∠ABD=∠A+∠ACB,∠EBD=∠ECB+∠BEC,
∴∠EBD= ∠ABD= (∠A+∠ACB)=∠BEC+∠ECB,即 ∠A+∠ECB=∠ECB+∠BEC,
∴∠BEC= ∠A= ;
_________
(3)结论:∠BQC=90°- ∠A.
理由如下:∵∠CBM与∠BCN是△ABC的外角,
∴∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,
∵BQ,CQ分别是∠ABC与∠ACB外角的平分线,
∴∠QBC= (∠A+∠ACB),∠QCB= (∠A+∠ABC).
∵∠QBC+∠QCB+∠BQC=180°,
∴∠BQC=180°-∠QBC-∠QCB,
=180°- (∠A+∠ACB)- (∠A+∠ABC),
=180°- ∠A- (∠A+∠ABC+∠ACB),
=180°- ∠A-90°
=90°- ∠A;
(4)由(3)可知,∠BQC=90°- ∠A=90°- =58°,
由(1)可知∠BPC=90°+ ∠BQC=90°+ =119°;
由(2)可知,∠R= ∠BQC=29°
故答案为119,29.
谢谢
