18.1.1平行四边形的性质第1课时 课件(共22张PPT)
文档属性
| 名称 | 18.1.1平行四边形的性质第1课时 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 21:09:44 | ||
图片预览






文档简介
(共22张PPT)
第18.1.1 平行四边形的性质
第1课时
人教版数学八年级下册
1.理解平行四边形的概念.
2.探索平行四边形对边、对角之间的关系.
3.利用平行四边形的性质解决实际问题.
学习目标
观察下列图片,你能从图片中发现哪些图形呢?
上图中你发现了哪些图形?你还能举出一些例子吗?
平行四边形
情境引入
观察下列图片,你能从图片中发现哪些图形呢?
你能说一说什么是平行四边形吗?
情境引入
D
C
A
B
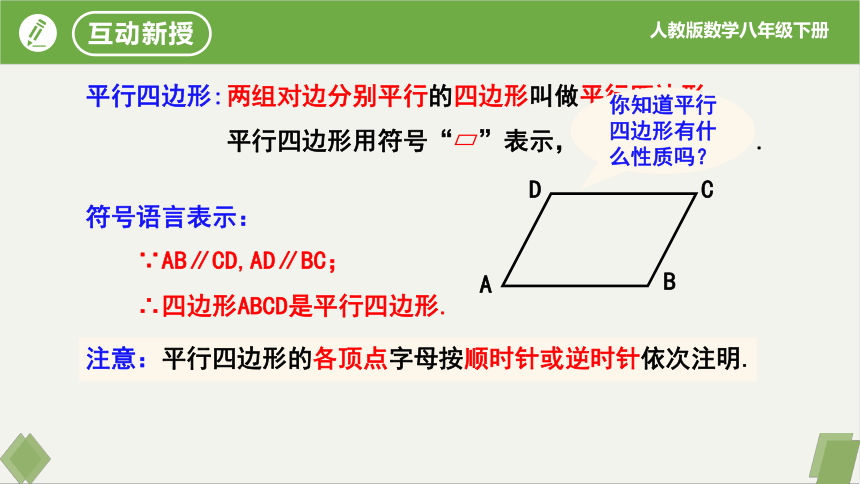
两组对边分别平行的四边形叫做平行四边形.
平行四边形用符号“ ”表示,记作“ ABCD”.
符号语言表示:
∵AB∥CD,AD∥BC;
∴四边形ABCD是平行四边形.
平行四边形:
你知道平行四边形有什么性质吗?
注意:平行四边形的各顶点字母按顺时针或逆时针依次注明.
互动新授
根据平行四边形的定义,我们知道平行四边形的两组对边分别平行.
除此之外,平行四边形还有什么性质呢?
探究
根据定义画一个平行四边形,观察这个四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?
互动新授
D
C
A
B
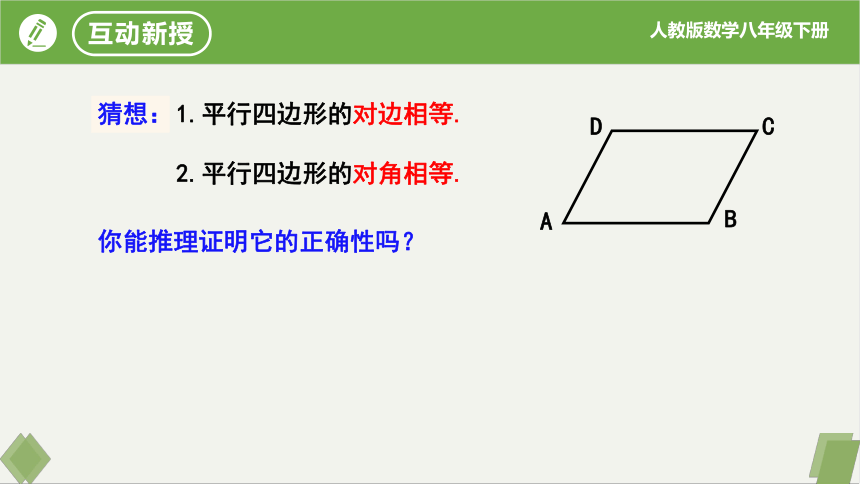
猜想:
2.平行四边形的对角相等.
1.平行四边形的对边相等.
你能推理证明它的正确性吗?
互动新授
A
B
C
D
如图,已知平行四边形ABCD,其中AB//CD,AD//BC,
求证:AB=CD,AD=BC,∠B=∠D,∠A=∠C.
分析:构造三角形,利用全等三角形的性质来得到对应边相等,对应角相等.在平行四边形中,连接任意一条对角线即可分成两个三角形.
互动新授
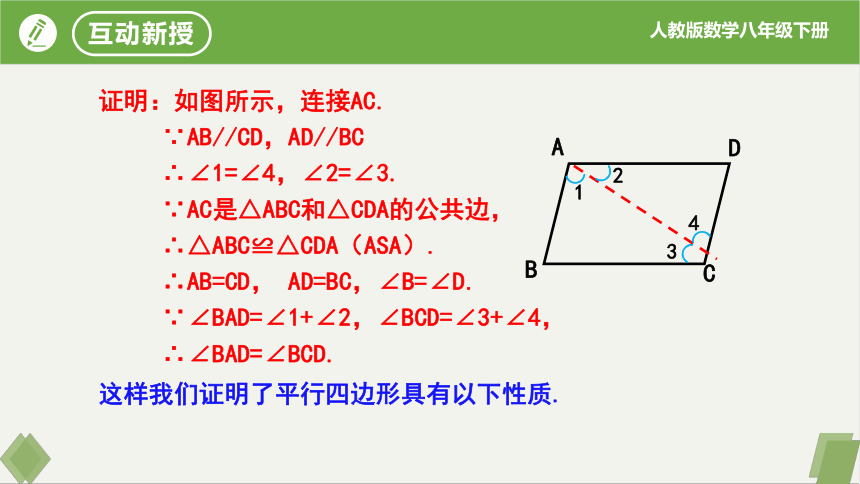
证明:如图所示,连接AC.
∵AB//CD,AD//BC
∴∠1=∠4,∠2=∠3.
∵AC是△ABC和△CDA的公共边,
∴△ABC≌△CDA(ASA).
∴AB=CD, AD=BC,∠B=∠D.
∵∠BAD=∠1+∠2,∠BCD=∠3+∠4,
∴∠BAD=∠BCD.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
3
4
这样我们证明了平行四边形具有以下性质.
互动新授
平行四边形的性质1:
平行四边形的对角相等.
平行四边形的对边相等.
平行四边形的性质2:
符号语言表示:
∵四边形ABCD是平行四边形;
∴AB=CD, AD=BC.
符号语言表示:
∵四边形ABCD是平行四边形;
∴∠B=∠D,∠A=∠C.
A
B
C
D
互动新授
例1 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS).
∴AE=CF.
D
A
B
C
F
E
典例精析
c
d
a
b
A C
B D
如图,a//b,c//d,c,d与a,b相交于A,B,C,D四点,由平行四边形的概念和性质可知,
四边形ABCD是平行四边形,AB=CD,
也就是说,两条平行线之间的任何两条平行线段都相等.
互动新授
a
b
A
B
从上面的结论可以知道,如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,a//b,A是a上的任意一点,AB⊥b,B是垂足,线段AB的长就是a,b之间的距离.
互动新授
1.如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠ABO=∠CDO B.∠BAD=∠BCD
C.AO=CO D.AC⊥BD
B
C
D
A
O
D
小试牛刀
1.小红不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了其中两块碎玻璃,其编号应该是( )
A.①,② B.①,④
C.③,④ D.②,③
2.在 ABCD中,∠A比∠D大70°,则∠C等于( )
A.70° B.100° C.110° D.125°
D
D
课堂检测
3.在 ABCD中,E、F是AC上的两点,AE=CF,求证:BE=DF.
A
B
C
D
E
F
证明:∵在 ABCD中,AB//CD
∴∠BAE=∠DCF
∵在△ABE 和△CDF中,AB=CD,
∠BAE=∠DCF, AE=CF
∴△ABE≌△CDF(SAS),
∴BE=DF.
课堂检测
1.如图,直线 AE//BD,点 C 在 BD上,若AE=5,BD=6,三角形ABD的面积为18,则三角形ACE的面积为 .
A
B
C
D
E
15
拓展训练
2.如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
解:S△ABC = AB BC,
= ×4×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
拓展训练
平行四边形的性质
概念
性质
两组对边分别平行的四边形叫做平行四边形.
①对边相等
②对角相等
两条平行线之间的距离
概念
性质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
两条平行线之间的平行线段相等.
课堂小结
1.已知直线a//b,点B、C、D是直线a上的三点,点A是直线b上一点,且AB=8、AC=5、AD=4,则两直线之间的距离( ).
A.等于4 B.小于4
C.不小于4 D.不大于4
b
A
a
C
B
D
D
课后作业
2.如图, ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
A
D
C
B
F
E
O
C
课后作业
谢谢聆听
第18.1.1 平行四边形的性质
第1课时
人教版数学八年级下册
1.理解平行四边形的概念.
2.探索平行四边形对边、对角之间的关系.
3.利用平行四边形的性质解决实际问题.
学习目标
观察下列图片,你能从图片中发现哪些图形呢?
上图中你发现了哪些图形?你还能举出一些例子吗?
平行四边形
情境引入
观察下列图片,你能从图片中发现哪些图形呢?
你能说一说什么是平行四边形吗?
情境引入
D
C
A
B
两组对边分别平行的四边形叫做平行四边形.
平行四边形用符号“ ”表示,记作“ ABCD”.
符号语言表示:
∵AB∥CD,AD∥BC;
∴四边形ABCD是平行四边形.
平行四边形:
你知道平行四边形有什么性质吗?
注意:平行四边形的各顶点字母按顺时针或逆时针依次注明.
互动新授
根据平行四边形的定义,我们知道平行四边形的两组对边分别平行.
除此之外,平行四边形还有什么性质呢?
探究
根据定义画一个平行四边形,观察这个四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?
互动新授
D
C
A
B
猜想:
2.平行四边形的对角相等.
1.平行四边形的对边相等.
你能推理证明它的正确性吗?
互动新授
A
B
C
D
如图,已知平行四边形ABCD,其中AB//CD,AD//BC,
求证:AB=CD,AD=BC,∠B=∠D,∠A=∠C.
分析:构造三角形,利用全等三角形的性质来得到对应边相等,对应角相等.在平行四边形中,连接任意一条对角线即可分成两个三角形.
互动新授
证明:如图所示,连接AC.
∵AB//CD,AD//BC
∴∠1=∠4,∠2=∠3.
∵AC是△ABC和△CDA的公共边,
∴△ABC≌△CDA(ASA).
∴AB=CD, AD=BC,∠B=∠D.
∵∠BAD=∠1+∠2,∠BCD=∠3+∠4,
∴∠BAD=∠BCD.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
3
4
这样我们证明了平行四边形具有以下性质.
互动新授
平行四边形的性质1:
平行四边形的对角相等.
平行四边形的对边相等.
平行四边形的性质2:
符号语言表示:
∵四边形ABCD是平行四边形;
∴AB=CD, AD=BC.
符号语言表示:
∵四边形ABCD是平行四边形;
∴∠B=∠D,∠A=∠C.
A
B
C
D
互动新授
例1 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS).
∴AE=CF.
D
A
B
C
F
E
典例精析
c
d
a
b
A C
B D
如图,a//b,c//d,c,d与a,b相交于A,B,C,D四点,由平行四边形的概念和性质可知,
四边形ABCD是平行四边形,AB=CD,
也就是说,两条平行线之间的任何两条平行线段都相等.
互动新授
a
b
A
B
从上面的结论可以知道,如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,a//b,A是a上的任意一点,AB⊥b,B是垂足,线段AB的长就是a,b之间的距离.
互动新授
1.如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠ABO=∠CDO B.∠BAD=∠BCD
C.AO=CO D.AC⊥BD
B
C
D
A
O
D
小试牛刀
1.小红不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了其中两块碎玻璃,其编号应该是( )
A.①,② B.①,④
C.③,④ D.②,③
2.在 ABCD中,∠A比∠D大70°,则∠C等于( )
A.70° B.100° C.110° D.125°
D
D
课堂检测
3.在 ABCD中,E、F是AC上的两点,AE=CF,求证:BE=DF.
A
B
C
D
E
F
证明:∵在 ABCD中,AB//CD
∴∠BAE=∠DCF
∵在△ABE 和△CDF中,AB=CD,
∠BAE=∠DCF, AE=CF
∴△ABE≌△CDF(SAS),
∴BE=DF.
课堂检测
1.如图,直线 AE//BD,点 C 在 BD上,若AE=5,BD=6,三角形ABD的面积为18,则三角形ACE的面积为 .
A
B
C
D
E
15
拓展训练
2.如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
解:S△ABC = AB BC,
= ×4×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
拓展训练
平行四边形的性质
概念
性质
两组对边分别平行的四边形叫做平行四边形.
①对边相等
②对角相等
两条平行线之间的距离
概念
性质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
两条平行线之间的平行线段相等.
课堂小结
1.已知直线a//b,点B、C、D是直线a上的三点,点A是直线b上一点,且AB=8、AC=5、AD=4,则两直线之间的距离( ).
A.等于4 B.小于4
C.不小于4 D.不大于4
b
A
a
C
B
D
D
课后作业
2.如图, ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
A
D
C
B
F
E
O
C
课后作业
谢谢聆听
