18.1.1平行四边形的性质第2课时(课件)-八年级数学下册同步课件 练习(人教版)
文档属性
| 名称 | 18.1.1平行四边形的性质第2课时(课件)-八年级数学下册同步课件 练习(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 659.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
第18.1.1 平行四边形的性质
第2课时
人教版数学八年级下册
1.探索并证明平行四边形对角线之间的关系.
2.利用平行四边形的性质解决实际问题.
学习目标
D
C
A
B
两组对边分别平行的四边形叫做平行四边形.
平行四边形用符号“ ”表示,记作“ ABCD”.
符号语言表示:
∵AB∥CD,AD∥BC;
∴四边形ABCD是平行四边形.
平行四边形:
你知道平行四边形有什么性质吗?
复习引入
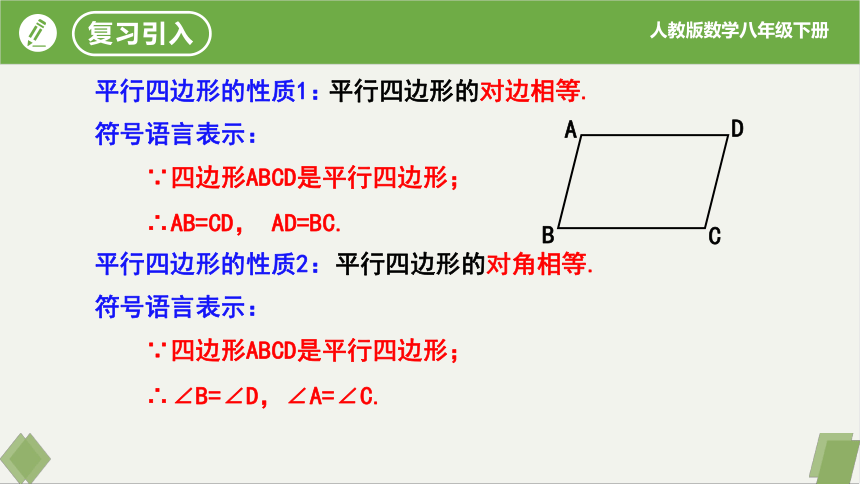
平行四边形的性质1:
平行四边形的对角相等.
平行四边形的对边相等.
平行四边形的性质2:
符号语言表示:
∵四边形ABCD是平行四边形;
∴AB=CD, AD=BC.
符号语言表示:
∵四边形ABCD是平行四边形;
∴∠B=∠D,∠A=∠C.
A
B
C
D
复习引入
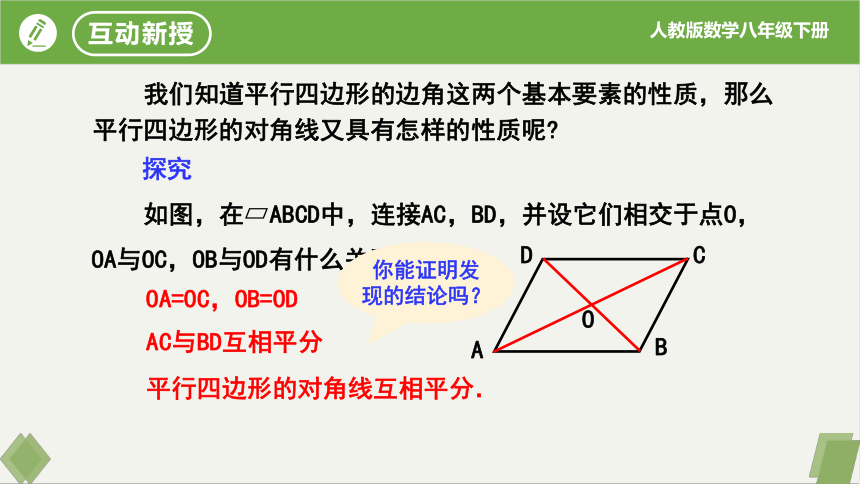
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢
探究
如图,在 ABCD中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?
D
C
A
B
O
平行四边形的对角线互相平分.
OA=OC,OB=OD
AC与BD互相平分
你能证明发现的结论吗?
互动新授
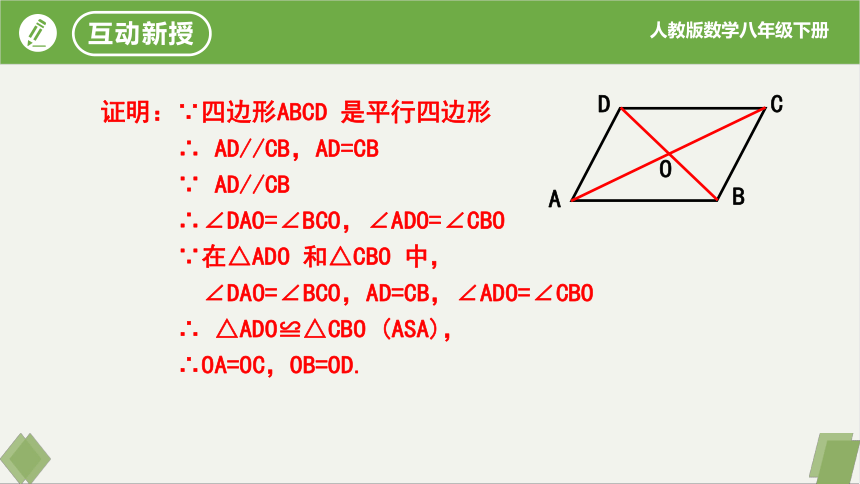
证明:∵四边形ABCD 是平行四边形
∴ AD//CB,AD=CB
∵ AD//CB
∴∠DAO=∠BCO,∠ADO=∠CBO
∵在△ADO 和△CBO 中,
∠DAO=∠BCO,AD=CB,∠ADO=∠CBO
∴ △ADO≌△CBO (ASA),
∴OA=OC,OB=OD.
D
C
A
B
O
互动新授
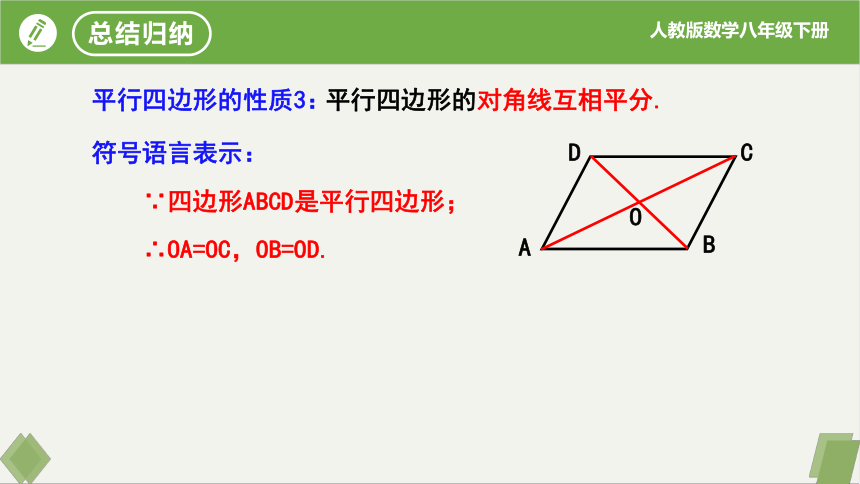
平行四边形的性质3:
平行四边形的对角线互相平分.
符号语言表示:
∵四边形ABCD是平行四边形;
∴OA=OC,OB=OD.
D
C
A
B
O
总结归纳
例2 如图,在 ABCD中,AB=10,AD=8,AC⊥BC.求BC、CD、AC、OA的长,以及 ABCD的面积.
解:∵四边形ABCD 是平行四边形
∴BC=AD=8,CD=AB=10
∵AC⊥BC
∴△ABC是直角三角形
根据勾股定理得:
∵OA=OC
∴OA= AC=3
∴S ABCD=BC·AC=8×6=48.
典例精析
1.如图,在 ABCD中,下列结论不一定成立的是( )
A.∠1=∠2 B.AC=BD
C.∠ADC=∠CBA D.OA=OC
B
小试牛刀
2.如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
B
小试牛刀
1.如图, ABCD的对角线交于点O,且AB=9,△OCD的周长为27,则平行四边形ABCD的两条对角线的和是( )
A.18 B.28 C.36 D.46
C
课堂检测
2.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_____.
5
课堂检测
3.如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式
可得5x=10(24-x),
解得x=16.
∴S ABCD=5×16=80.
课堂检测
1.如图,已知O是平行四边形ABCD的对角线的交点,AC=24,BD=18,AB=16,求△OCD的周长及AD边的取值范围.
解:由题意得OA=OC=12,OB=OD=9,CD=AB=16,
∴△OCD的周长为12+9+16=37.
在△ACD中,24-16<AD<24+16,∴8<AD<40;
在△ABD中,18-16<AD<18+16,∴2<AD<34;
在△AOD中,12-9<AD<12+9,∴3<AD<21.
综上所述,AD的取值范围应是8<AD<21.
拓展训练
2.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴C ABCD=2×(BC+CD)=20.
拓展训练
平行四边形的性质3:
平行四边形的对角线互相平分.
符号语言表示:
∵四边形ABCD是平行四边形;
∴OA=OC,OB=OD.
D
C
A
B
O
课堂小结
1.如图,在 ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是 ( )
A.9 B.18 C.27 D.36
B
课后作业
2.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:S=(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
课后作业
谢谢聆听
第18.1.1 平行四边形的性质
第2课时
人教版数学八年级下册
1.探索并证明平行四边形对角线之间的关系.
2.利用平行四边形的性质解决实际问题.
学习目标
D
C
A
B
两组对边分别平行的四边形叫做平行四边形.
平行四边形用符号“ ”表示,记作“ ABCD”.
符号语言表示:
∵AB∥CD,AD∥BC;
∴四边形ABCD是平行四边形.
平行四边形:
你知道平行四边形有什么性质吗?
复习引入
平行四边形的性质1:
平行四边形的对角相等.
平行四边形的对边相等.
平行四边形的性质2:
符号语言表示:
∵四边形ABCD是平行四边形;
∴AB=CD, AD=BC.
符号语言表示:
∵四边形ABCD是平行四边形;
∴∠B=∠D,∠A=∠C.
A
B
C
D
复习引入
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢
探究
如图,在 ABCD中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?
D
C
A
B
O
平行四边形的对角线互相平分.
OA=OC,OB=OD
AC与BD互相平分
你能证明发现的结论吗?
互动新授
证明:∵四边形ABCD 是平行四边形
∴ AD//CB,AD=CB
∵ AD//CB
∴∠DAO=∠BCO,∠ADO=∠CBO
∵在△ADO 和△CBO 中,
∠DAO=∠BCO,AD=CB,∠ADO=∠CBO
∴ △ADO≌△CBO (ASA),
∴OA=OC,OB=OD.
D
C
A
B
O
互动新授
平行四边形的性质3:
平行四边形的对角线互相平分.
符号语言表示:
∵四边形ABCD是平行四边形;
∴OA=OC,OB=OD.
D
C
A
B
O
总结归纳
例2 如图,在 ABCD中,AB=10,AD=8,AC⊥BC.求BC、CD、AC、OA的长,以及 ABCD的面积.
解:∵四边形ABCD 是平行四边形
∴BC=AD=8,CD=AB=10
∵AC⊥BC
∴△ABC是直角三角形
根据勾股定理得:
∵OA=OC
∴OA= AC=3
∴S ABCD=BC·AC=8×6=48.
典例精析
1.如图,在 ABCD中,下列结论不一定成立的是( )
A.∠1=∠2 B.AC=BD
C.∠ADC=∠CBA D.OA=OC
B
小试牛刀
2.如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
B
小试牛刀
1.如图, ABCD的对角线交于点O,且AB=9,△OCD的周长为27,则平行四边形ABCD的两条对角线的和是( )
A.18 B.28 C.36 D.46
C
课堂检测
2.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_____.
5
课堂检测
3.如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式
可得5x=10(24-x),
解得x=16.
∴S ABCD=5×16=80.
课堂检测
1.如图,已知O是平行四边形ABCD的对角线的交点,AC=24,BD=18,AB=16,求△OCD的周长及AD边的取值范围.
解:由题意得OA=OC=12,OB=OD=9,CD=AB=16,
∴△OCD的周长为12+9+16=37.
在△ACD中,24-16<AD<24+16,∴8<AD<40;
在△ABD中,18-16<AD<18+16,∴2<AD<34;
在△AOD中,12-9<AD<12+9,∴3<AD<21.
综上所述,AD的取值范围应是8<AD<21.
拓展训练
2.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴C ABCD=2×(BC+CD)=20.
拓展训练
平行四边形的性质3:
平行四边形的对角线互相平分.
符号语言表示:
∵四边形ABCD是平行四边形;
∴OA=OC,OB=OD.
D
C
A
B
O
课堂小结
1.如图,在 ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是 ( )
A.9 B.18 C.27 D.36
B
课后作业
2.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:S=(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
课后作业
谢谢聆听
