18.1.2平行四边形的判定第1课时(课件)-八年级数学下册同步课件 练习(人教版)
文档属性
| 名称 | 18.1.2平行四边形的判定第1课时(课件)-八年级数学下册同步课件 练习(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 710.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 09:29:17 | ||
图片预览




文档简介
(共27张PPT)
第18.1.2 平行四边形的判定
第1课时
人教版数学八年级下册
1.通过平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路.
2.掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
学习目标
D
C
A
B
平行四边形的性质1:
平行四边形的对角相等.
平行四边形的对边相等.
平行四边形的性质2:
平行四边形的性质3:
平行四边形的对角线互相平分.
复习引入
思考
通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分.
反过来,对边相等,或对角相等,或对角线互相平分的四边形是平行四边形吗?
也就是说,平行四边形的性质定理的逆命题成立吗?
你能得出什么猜想呢?
互动新授
猜想1:
猜想2:
猜想3:
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
你能根据平行四边形的定义证明它们吗?
互动新授
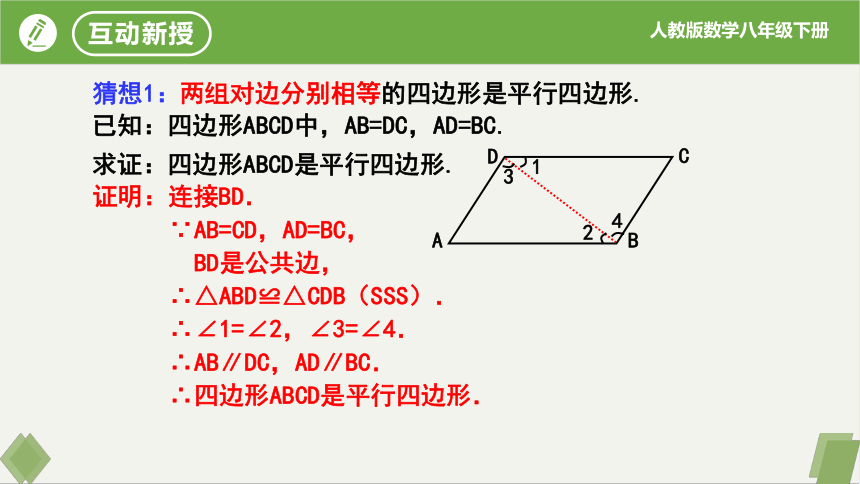
猜想1:
两组对边分别相等的四边形是平行四边形.
证明:连接BD.
∵AB=CD,AD=BC,
BD是公共边,
∴△ABD≌△CDB(SSS).
∴∠1=∠2,∠3=∠4.
∴AB∥DC,AD∥BC.
∴四边形ABCD是平行四边形.
已知:四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
互动新授
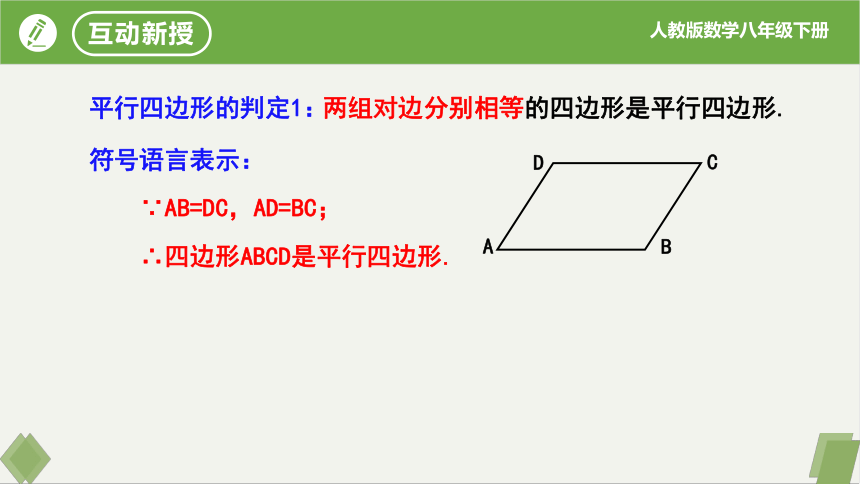
平行四边形的判定1:
两组对边分别相等的四边形是平行四边形.
D
A
B
C
符号语言表示:
∵AB=DC,AD=BC;
∴四边形ABCD是平行四边形.
互动新授
猜想2:
D
A
B
C
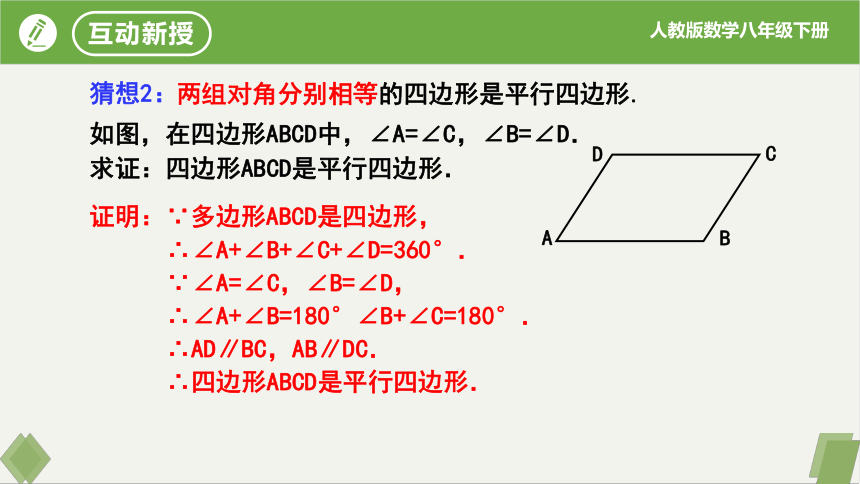
两组对角分别相等的四边形是平行四边形.
证明:∵多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°∠B+∠C=180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
互动新授
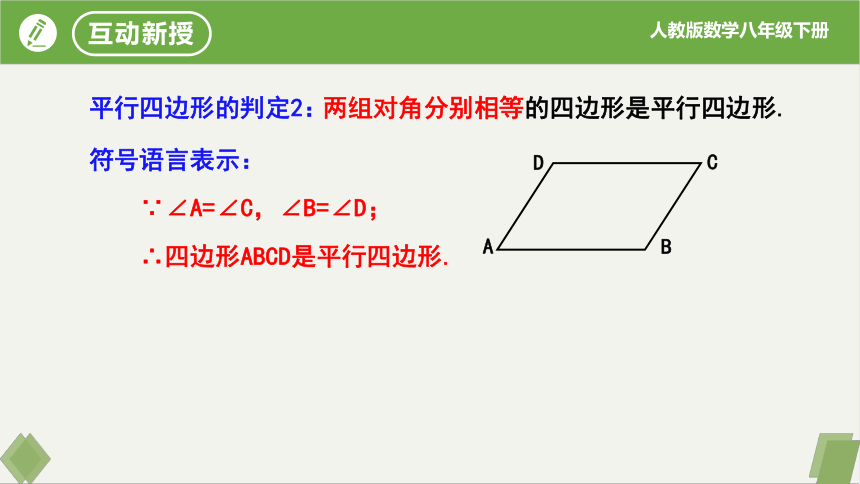
平行四边形的判定2:
两组对角分别相等的四边形是平行四边形.
D
A
B
C
符号语言表示:
∵∠A=∠C,∠B=∠D;
∴四边形ABCD是平行四边形.
互动新授
猜想3:
对角线互相平分的四边形是平行四边形.
如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
D
A
B
C
O
证明:∵OA=OC,OB=OD,∠1=∠2,
∴△AOD≌△COB(SAS).
∴∠3=∠4.
∴AD∥BC.
同理 AB∥DC.
∴四边形ABCD是平行四边形.
1
2
3
4
互动新授
平行四边形的判定3:
对角线互相平分的四边形是平行四边形.
符号语言表示:
∵OA=OC,OB=OD;
∴四边形ABCD是平行四边形.
D
A
B
C
O
互动新授
例3 如图, ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF,
∴ AO-AE=CO-CF,即EO=OF.
∵BO=DO,
∴四边形BFDE是平行四边形.
典例精析
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
我们猜想:一组对边平行且相等的四边形是平行四边形.
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
你能证明它的正确性吗?
互动新授
B
D
A
C
1
2
如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB//CD,
∴∠1=∠2.
∵AB=CD,AC=CA
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形.
互动新授
平行四边形的判定4:
一组对边平行且相等的四边形是平行四边形.
D
A
B
C
符号语言表示:
∵AB//CD,AB=CD;
∴四边形ABCD是平行四边形.
互动新授
例4 如图,在 ABCD中,E、F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,EB//FD.
∵EB= AB,FD= CD,
∴EB=FD.
∴四边形EBFD是平行四边形.
D
A
B
C
E
F
典例精析
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
小试牛刀
2.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.
证明:∵DE=DC,
∴∠DEC=∠C.
∵∠B=∠C,
∴∠B=∠DEC,
∴AB∥BE,
∵AD∥BC,
∴四边形ABED是平行四边形.
∴AD=BE.
小试牛刀
1.如图,在四边形ABCD中,AC与BD交于点O.如果AC=8cm,BD=10cm,那么当AO=____cm,BO=____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
4
5
课堂检测
2.如图,在四边形ABCD中,
(1)如果AB∥CD,AD∥BC,那么四边形ABCD是___________.
(2)如果∠A:∠B:∠ C:∠D=a:b:a:b(a,b为正数),那么四边形ABCD是__________.
(3)如果AD=6cm,AB=4cm,那么当BC=____cm,CD=____cm时,四边形ABCD为平行四边形.
B
D
A
C
平行四边形
平行四边形
6
4
课堂检测
3.如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
∵∠B=∠DEF,∠ACB=∠F,
∴△ABC≌△DEF,
∴AB=DE.
∵∠B=∠DEF,
∴AB∥DE.
∴四边形ABED是平行四边形.
课堂检测
1.如图,五边形ABCDE是正五边形,连接BD、CE,交于点P.
求证:四边形ABPE是平行四边形.
A
B
C
D
E
P
证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.
拓展训练
2.如图,△ABC中,AB=AC=10,D是BC边上的任意一点,分别作DF∥AB交AC于F,DE∥AC交AB于E,求DE+DF的值.
解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF.
∵AB=AC=10,
∴∠B=∠C.
∵DF∥AB,
∴∠CDF=∠B,
∴∠CDF=∠C,
∴DF=CF,
∴DE+DF=AF+FC=AC=10.
拓展训练
平行四边形的判定1:
两组对边分别相等的四边形是平行四边形.
平行四边形的判定2:
两组对角分别相等的四边形是平行四边形.
平行四边形的判定3:
对角线互相平分的四边形是平行四边形.
平行四边形的判定4:
一组对边平行且相等的四边形是平行四边形.
课堂小结
1.如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
课后作业
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥EF,AD=EF,EF∥BC,EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
2.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
课后作业
谢谢聆听
第18.1.2 平行四边形的判定
第1课时
人教版数学八年级下册
1.通过平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路.
2.掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
学习目标
D
C
A
B
平行四边形的性质1:
平行四边形的对角相等.
平行四边形的对边相等.
平行四边形的性质2:
平行四边形的性质3:
平行四边形的对角线互相平分.
复习引入
思考
通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分.
反过来,对边相等,或对角相等,或对角线互相平分的四边形是平行四边形吗?
也就是说,平行四边形的性质定理的逆命题成立吗?
你能得出什么猜想呢?
互动新授
猜想1:
猜想2:
猜想3:
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
你能根据平行四边形的定义证明它们吗?
互动新授
猜想1:
两组对边分别相等的四边形是平行四边形.
证明:连接BD.
∵AB=CD,AD=BC,
BD是公共边,
∴△ABD≌△CDB(SSS).
∴∠1=∠2,∠3=∠4.
∴AB∥DC,AD∥BC.
∴四边形ABCD是平行四边形.
已知:四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
互动新授
平行四边形的判定1:
两组对边分别相等的四边形是平行四边形.
D
A
B
C
符号语言表示:
∵AB=DC,AD=BC;
∴四边形ABCD是平行四边形.
互动新授
猜想2:
D
A
B
C
两组对角分别相等的四边形是平行四边形.
证明:∵多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°∠B+∠C=180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
互动新授
平行四边形的判定2:
两组对角分别相等的四边形是平行四边形.
D
A
B
C
符号语言表示:
∵∠A=∠C,∠B=∠D;
∴四边形ABCD是平行四边形.
互动新授
猜想3:
对角线互相平分的四边形是平行四边形.
如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
D
A
B
C
O
证明:∵OA=OC,OB=OD,∠1=∠2,
∴△AOD≌△COB(SAS).
∴∠3=∠4.
∴AD∥BC.
同理 AB∥DC.
∴四边形ABCD是平行四边形.
1
2
3
4
互动新授
平行四边形的判定3:
对角线互相平分的四边形是平行四边形.
符号语言表示:
∵OA=OC,OB=OD;
∴四边形ABCD是平行四边形.
D
A
B
C
O
互动新授
例3 如图, ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF,
∴ AO-AE=CO-CF,即EO=OF.
∵BO=DO,
∴四边形BFDE是平行四边形.
典例精析
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
我们猜想:一组对边平行且相等的四边形是平行四边形.
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
你能证明它的正确性吗?
互动新授
B
D
A
C
1
2
如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB//CD,
∴∠1=∠2.
∵AB=CD,AC=CA
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形.
互动新授
平行四边形的判定4:
一组对边平行且相等的四边形是平行四边形.
D
A
B
C
符号语言表示:
∵AB//CD,AB=CD;
∴四边形ABCD是平行四边形.
互动新授
例4 如图,在 ABCD中,E、F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,EB//FD.
∵EB= AB,FD= CD,
∴EB=FD.
∴四边形EBFD是平行四边形.
D
A
B
C
E
F
典例精析
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
小试牛刀
2.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.
证明:∵DE=DC,
∴∠DEC=∠C.
∵∠B=∠C,
∴∠B=∠DEC,
∴AB∥BE,
∵AD∥BC,
∴四边形ABED是平行四边形.
∴AD=BE.
小试牛刀
1.如图,在四边形ABCD中,AC与BD交于点O.如果AC=8cm,BD=10cm,那么当AO=____cm,BO=____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
4
5
课堂检测
2.如图,在四边形ABCD中,
(1)如果AB∥CD,AD∥BC,那么四边形ABCD是___________.
(2)如果∠A:∠B:∠ C:∠D=a:b:a:b(a,b为正数),那么四边形ABCD是__________.
(3)如果AD=6cm,AB=4cm,那么当BC=____cm,CD=____cm时,四边形ABCD为平行四边形.
B
D
A
C
平行四边形
平行四边形
6
4
课堂检测
3.如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
∵∠B=∠DEF,∠ACB=∠F,
∴△ABC≌△DEF,
∴AB=DE.
∵∠B=∠DEF,
∴AB∥DE.
∴四边形ABED是平行四边形.
课堂检测
1.如图,五边形ABCDE是正五边形,连接BD、CE,交于点P.
求证:四边形ABPE是平行四边形.
A
B
C
D
E
P
证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.
拓展训练
2.如图,△ABC中,AB=AC=10,D是BC边上的任意一点,分别作DF∥AB交AC于F,DE∥AC交AB于E,求DE+DF的值.
解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF.
∵AB=AC=10,
∴∠B=∠C.
∵DF∥AB,
∴∠CDF=∠B,
∴∠CDF=∠C,
∴DF=CF,
∴DE+DF=AF+FC=AC=10.
拓展训练
平行四边形的判定1:
两组对边分别相等的四边形是平行四边形.
平行四边形的判定2:
两组对角分别相等的四边形是平行四边形.
平行四边形的判定3:
对角线互相平分的四边形是平行四边形.
平行四边形的判定4:
一组对边平行且相等的四边形是平行四边形.
课堂小结
1.如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
课后作业
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥EF,AD=EF,EF∥BC,EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
2.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
课后作业
谢谢聆听
