18.1.2平行四边形的判定第2课时 课件(共18张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定第2课时 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 629.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 21:43:24 | ||
图片预览




文档简介
(共18张PPT)
第18.1.2 平行四边形的判定
第2课时
人教版数学八年级下册
1.理解三角形中位线的概念,掌握三角形中位线定理.
2.通过探索,猜想,证明三角形的中位线定理,进一步发展推理论证的能力.
学习目标
平行四边形的判定1:
两组对边分别相等的四边形是平行四边形.
平行四边形的判定2:
两组对角分别相等的四边形是平行四边形.
平行四边形的判定3:
对角线互相平分的四边形是平行四边形.
平行四边形的判定4:
一组对边平行且相等的四边形是平行四边形.
复习引入
前面我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质研究平行四边形的有关问题.
下面我们利用平行四边形研究三角形的有关问题.
互动新授
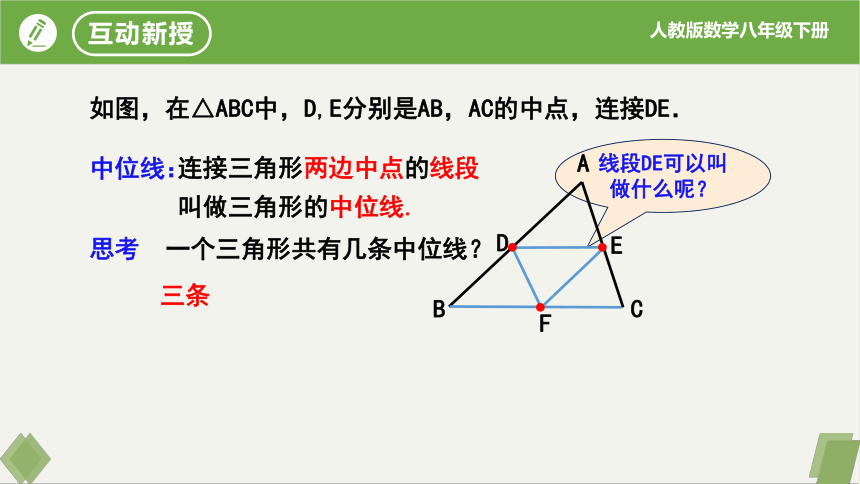
线段DE可以叫做什么呢?
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.
D
E
A
B
C
连接三角形两边中点的线段叫做三角形的中位线.
中位线:
思考 一个三角形共有几条中位线?
三条
F
.
.
.
互动新授
D
E
A
B
C
.
.
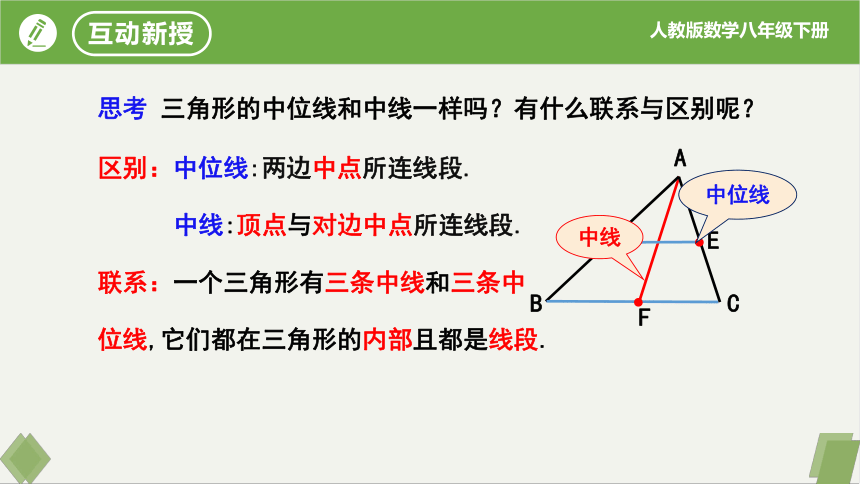
思考 三角形的中位线和中线一样吗?有什么联系与区别呢?
中位线
中线
F
.
区别:中位线:两边中点所连线段.
中线:顶点与对边中点所连线段.
联系:一个三角形有三条中线和三条中位线,它们都在三角形的内部且都是线段.
互动新授
D
E
A
B
C
.
.
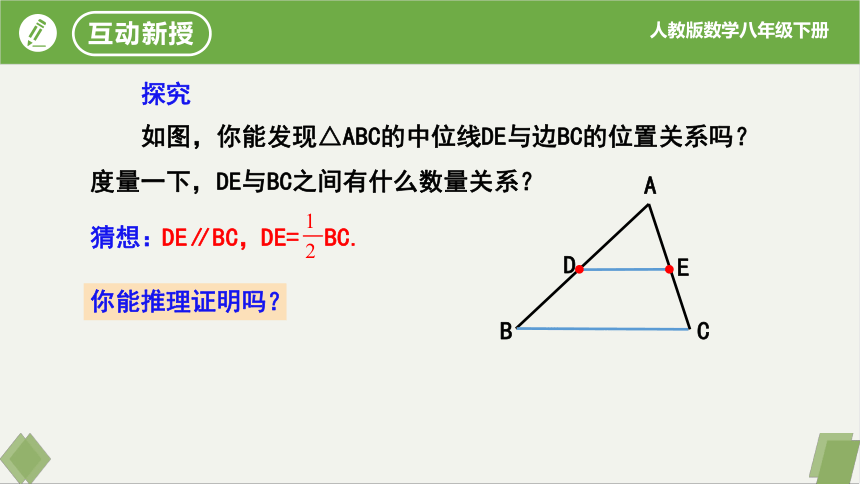
探究
如图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
猜想:
DE∥BC,
DE= BC.
你能推理证明吗?
互动新授
如图,D、E分别是△ABC的边AB、AC的中点.求证:DE∥BC,DE= BC.
D
E
A
B
C
.
.
互动新授
延长DE到F,使EF=DE,连接AF、CF、DC .
∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形.
∴CF AD.
∴CF BD.
∴四边形BCFD是平行四边形.
∴DF BC.
∵DE= DF,
∴DE∥BC,且DE= BC.
证明:
D
E
F
互动新授
通过上面证明,我们可以得到三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
D
E
A
B
C
.
.
符号语言表示:
∵D、E分别是边AB、AC的中点,
∴DE∥BC,DE= BC.
互动新授
2.如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是5,则△ABC的周长是( )
A.8 B.10 C.12 D.14
1.如图,EF为△ABC的中位线,若AB=6,则EF的长为( )
A.2 B.3 C.4 D.5
B
B
小试牛刀
证明:∵CD=CA, CF平分∠ACB,
∴FA=FD(三线合一),
∵FA=FD,AE=EB,
∴EF= BD.
1.如图,在△ABC中,点D在BC上,CD=CA,CF平分∠ACB,AE=EB,求证:EF=BD
课堂检测
2.已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.
(1)求证:四边形CDEF是平行四边形;
(2)若EF=2cm,求AB的长.
(1)证明:∵D、E分别是AB、AC的中点,
∴ED是Rt△ABC的中位线,∴ED∥FC.
∵EF∥DC,∴四边形CDEF是平行四边形;
(2)∵四边形CDEF是平行四边形∴DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,∴DC= AB,
∴AB=2DC=4cm.
课堂检测
1.如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
解:∵M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM= AB,PN= DC,PM∥AB,PN∥DC,
∵AB=CD,∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+(180° ∠NPB)=130°,
∴∠PMN=(180° 130°)÷ 2 =25°.
拓展训练
中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
D
E
A
B
C
.
.
符号语言表示:
∵D、E分别是边AB、AC的中点,
∴DE∥BC,DE= BC.
课堂小结
1.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴C△DOE=OD+OE+DE= (BD+BC+CD)=15.
课后作业
2.如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠DFA=∠FAB.
∵AF平分∠CAB,
∴∠DAF=∠FAB,
∴∠DAF=∠DFA,
∴AD=DF=3,
∴AC=2AD=2DF=6.
课后作业
谢谢聆听
第18.1.2 平行四边形的判定
第2课时
人教版数学八年级下册
1.理解三角形中位线的概念,掌握三角形中位线定理.
2.通过探索,猜想,证明三角形的中位线定理,进一步发展推理论证的能力.
学习目标
平行四边形的判定1:
两组对边分别相等的四边形是平行四边形.
平行四边形的判定2:
两组对角分别相等的四边形是平行四边形.
平行四边形的判定3:
对角线互相平分的四边形是平行四边形.
平行四边形的判定4:
一组对边平行且相等的四边形是平行四边形.
复习引入
前面我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质研究平行四边形的有关问题.
下面我们利用平行四边形研究三角形的有关问题.
互动新授
线段DE可以叫做什么呢?
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.
D
E
A
B
C
连接三角形两边中点的线段叫做三角形的中位线.
中位线:
思考 一个三角形共有几条中位线?
三条
F
.
.
.
互动新授
D
E
A
B
C
.
.
思考 三角形的中位线和中线一样吗?有什么联系与区别呢?
中位线
中线
F
.
区别:中位线:两边中点所连线段.
中线:顶点与对边中点所连线段.
联系:一个三角形有三条中线和三条中位线,它们都在三角形的内部且都是线段.
互动新授
D
E
A
B
C
.
.
探究
如图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
猜想:
DE∥BC,
DE= BC.
你能推理证明吗?
互动新授
如图,D、E分别是△ABC的边AB、AC的中点.求证:DE∥BC,DE= BC.
D
E
A
B
C
.
.
互动新授
延长DE到F,使EF=DE,连接AF、CF、DC .
∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形.
∴CF AD.
∴CF BD.
∴四边形BCFD是平行四边形.
∴DF BC.
∵DE= DF,
∴DE∥BC,且DE= BC.
证明:
D
E
F
互动新授
通过上面证明,我们可以得到三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
D
E
A
B
C
.
.
符号语言表示:
∵D、E分别是边AB、AC的中点,
∴DE∥BC,DE= BC.
互动新授
2.如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是5,则△ABC的周长是( )
A.8 B.10 C.12 D.14
1.如图,EF为△ABC的中位线,若AB=6,则EF的长为( )
A.2 B.3 C.4 D.5
B
B
小试牛刀
证明:∵CD=CA, CF平分∠ACB,
∴FA=FD(三线合一),
∵FA=FD,AE=EB,
∴EF= BD.
1.如图,在△ABC中,点D在BC上,CD=CA,CF平分∠ACB,AE=EB,求证:EF=BD
课堂检测
2.已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.
(1)求证:四边形CDEF是平行四边形;
(2)若EF=2cm,求AB的长.
(1)证明:∵D、E分别是AB、AC的中点,
∴ED是Rt△ABC的中位线,∴ED∥FC.
∵EF∥DC,∴四边形CDEF是平行四边形;
(2)∵四边形CDEF是平行四边形∴DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,∴DC= AB,
∴AB=2DC=4cm.
课堂检测
1.如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
解:∵M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM= AB,PN= DC,PM∥AB,PN∥DC,
∵AB=CD,∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+(180° ∠NPB)=130°,
∴∠PMN=(180° 130°)÷ 2 =25°.
拓展训练
中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
D
E
A
B
C
.
.
符号语言表示:
∵D、E分别是边AB、AC的中点,
∴DE∥BC,DE= BC.
课堂小结
1.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴C△DOE=OD+OE+DE= (BD+BC+CD)=15.
课后作业
2.如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠DFA=∠FAB.
∵AF平分∠CAB,
∴∠DAF=∠FAB,
∴∠DAF=∠DFA,
∴AD=DF=3,
∴AC=2AD=2DF=6.
课后作业
谢谢聆听
