18.2.1 矩形 课件(共19张PPT)
文档属性
| 名称 | 18.2.1 矩形 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 12:24:46 | ||
图片预览



文档简介
(共19张PPT)
18.2.1矩形
18.2.1矩形
学习目标:
1.理解矩形的概念,明确矩形和平行四边形的区别与联系;
2.探索并证明矩形的性质,会用矩形性质解决问题;
3.理解“直角三角形斜边上的中线等于斜边一半”的性质,并能初步运用
重点:矩形特殊性质的发现,证明
难点:矩形特殊性质的应用
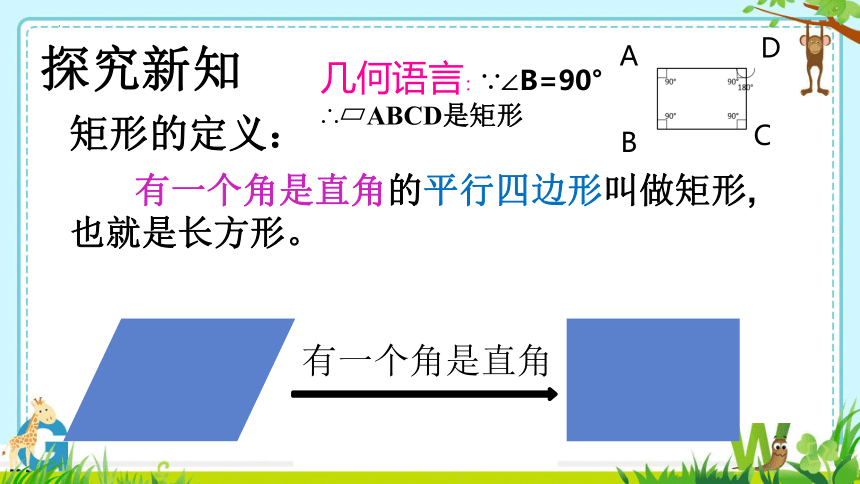
矩形的定义:
有一个角是直角的平行四边形叫做矩形,也就是长方形。
有一个角是直角
探究新知
几何语言:∵∠B=90°
∴ ABCD是矩形
A
B
C
D
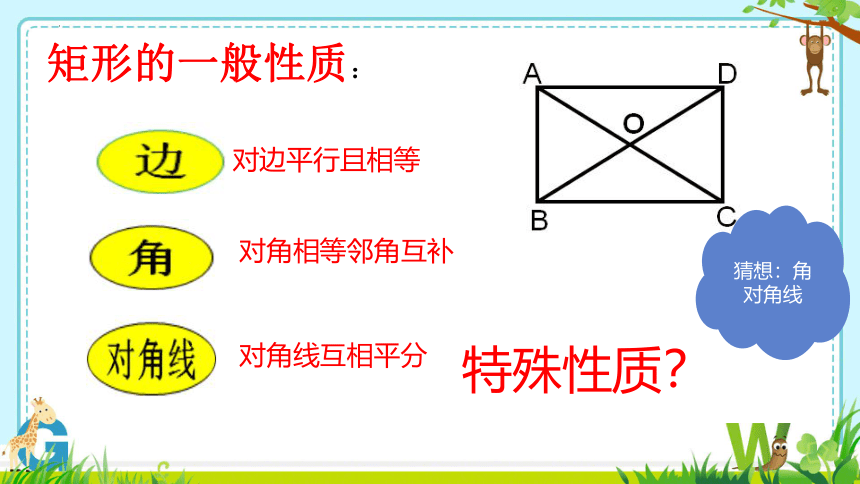
矩形的一般性质:
对边平行且相等
对角相等邻角互补
对角线互相平分
特殊性质?
猜想:角
对角线
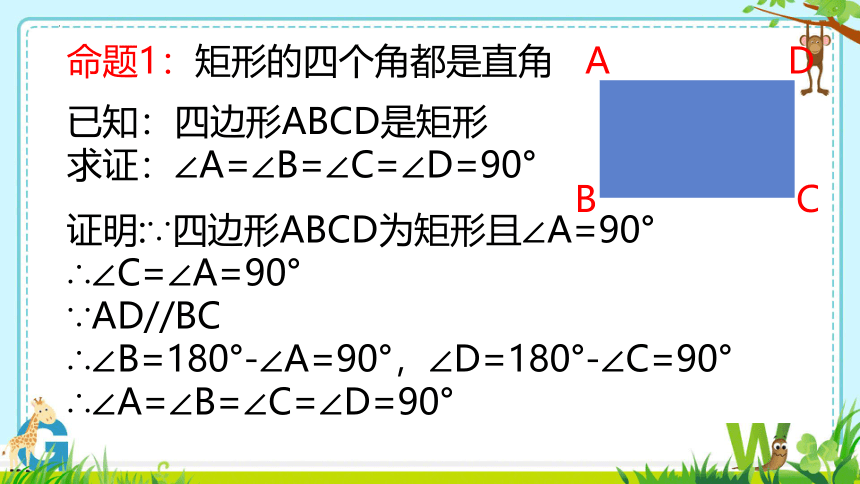
命题1:矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:∵四边形ABCD为矩形且∠A=90°
∴∠C=∠A=90°
∵AD//BC
∴∠B=180°-∠A=90°,∠D=180°-∠C=90°
∴∠A=∠B=∠C=∠D=90°
命题2:矩形的对角线相等
已知:四边形ABCD是矩形
求证:AC=BD
证明:在矩形ABCD中
AB=CD,∠ABC=∠DCB=90°,
又BC=CB
∴△ABC △DCB(SAS)
∴AC=BD
经过证明得出矩形的性质,让学生学会把文字语言转化为几何语言,为今后准确运用矩形的性质证题打基础。
活动设计
运用动画功能显示文本
使用说明
性质1:矩形的四个角都是直角
性质2:矩形的对角线相等
几何语言:
∵四边形ABCD为矩形
∴∠BAD=∠ABC=∠BCD=∠ADC=900
AC=BD
命题1:矩形的四个角都是直角
命题2:矩形的对角线相等
设计填表活动,通过比较平行四边形和矩形的性质,加深对矩形性质的理解。
活动设计
运用表格功能绘制表格。添加遮罩功能遮盖答案。运用触发动画功能。运用班级优化大师随机抽选学生回答,学生答题后再点击去除遮罩,答对的学生予以加分。
使用说明
类比归纳
轴对称图形
1、矩形具有而平行四边行不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
B
2.如图,四边形ABCD是矩形
A
B
C
D
O
(1)若∠AOD=50°,则∠OAD= ,
∠OAB= ,
∠AOB= ,
∠ACD= 。
(2)若AD=6,AB=8,则BD= ,AC= ,OB= .
65°
25°
130°
25°
10
10
5
新发现
两对全等的等腰三角形
四个全等的直角三角形
矩形问题通常可以转化为等腰三角形或直角三角形来解决
设计填空题,探究直角三角形的性质,教师提问学生回答,同步擦除蒙层显示答案,归纳结论。
活动设计
运用蒙层功能遮挡答案。运用触发动画功能显示文本。
使用说明
∵四边形ABCD是矩形,
∴AC=BD.
OA= = AC,OB= = BD .
∴ OA= BD,OB= AC.
再探新知
直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
几何语言:∵在Rt△ABC中,OB是斜边AC的中线
3、在Rt△ABC 中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为 。
4.在直角三角形ABC中,两直角边分别为5和12,则斜边上的中线为 。
对到目前为止学过的直角三角形的性质加以总结
活动设计
运用思维导图功能进行总结
使用说明
总结归纳
如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分。
∴ OA = OB
又 ∵ ∠AOB=60°,
∴ ΔOAB是等边三角形
∴OA=AB=4(cm)
∴ AC=BD = 2OA=2×4=8(cm)
例题精析
A
B
C
D
O
回顾反思
1.矩形定义及性质
2.直角三角形斜边上的中线等于斜边一半
分层布置作业,让不同能力的学生有不同收获
活动设计
运用形状功能绘图
使用说明
作业
1.矩形ABCD的对角线AC =6cm,则另一条对角线BD=_______。
2.已知矩形ABCD,AC=8,则BD= ,OD= 。
3.已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 , , .
4.已知矩形的周长是24cm,相邻两边之比是 1:2,那么这个矩形
的边长分别是 ,对角线长是_________.
5.如图,已知矩形ABCD,AC=4,则BD= ,∠ABC= _ °
若∠ADB=30°,则∠AOD= °;∠COD= AB=____,AD=______.
6.矩形不一定具有的性质是( )
A、对角线相等 B、四个角相等 C、是轴对称图形 D、对角线互相垂直
A
B
C
D
O
7.求证:矩形的对角线相等
18.2.1矩形
18.2.1矩形
学习目标:
1.理解矩形的概念,明确矩形和平行四边形的区别与联系;
2.探索并证明矩形的性质,会用矩形性质解决问题;
3.理解“直角三角形斜边上的中线等于斜边一半”的性质,并能初步运用
重点:矩形特殊性质的发现,证明
难点:矩形特殊性质的应用
矩形的定义:
有一个角是直角的平行四边形叫做矩形,也就是长方形。
有一个角是直角
探究新知
几何语言:∵∠B=90°
∴ ABCD是矩形
A
B
C
D
矩形的一般性质:
对边平行且相等
对角相等邻角互补
对角线互相平分
特殊性质?
猜想:角
对角线
命题1:矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:∵四边形ABCD为矩形且∠A=90°
∴∠C=∠A=90°
∵AD//BC
∴∠B=180°-∠A=90°,∠D=180°-∠C=90°
∴∠A=∠B=∠C=∠D=90°
命题2:矩形的对角线相等
已知:四边形ABCD是矩形
求证:AC=BD
证明:在矩形ABCD中
AB=CD,∠ABC=∠DCB=90°,
又BC=CB
∴△ABC △DCB(SAS)
∴AC=BD
经过证明得出矩形的性质,让学生学会把文字语言转化为几何语言,为今后准确运用矩形的性质证题打基础。
活动设计
运用动画功能显示文本
使用说明
性质1:矩形的四个角都是直角
性质2:矩形的对角线相等
几何语言:
∵四边形ABCD为矩形
∴∠BAD=∠ABC=∠BCD=∠ADC=900
AC=BD
命题1:矩形的四个角都是直角
命题2:矩形的对角线相等
设计填表活动,通过比较平行四边形和矩形的性质,加深对矩形性质的理解。
活动设计
运用表格功能绘制表格。添加遮罩功能遮盖答案。运用触发动画功能。运用班级优化大师随机抽选学生回答,学生答题后再点击去除遮罩,答对的学生予以加分。
使用说明
类比归纳
轴对称图形
1、矩形具有而平行四边行不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
B
2.如图,四边形ABCD是矩形
A
B
C
D
O
(1)若∠AOD=50°,则∠OAD= ,
∠OAB= ,
∠AOB= ,
∠ACD= 。
(2)若AD=6,AB=8,则BD= ,AC= ,OB= .
65°
25°
130°
25°
10
10
5
新发现
两对全等的等腰三角形
四个全等的直角三角形
矩形问题通常可以转化为等腰三角形或直角三角形来解决
设计填空题,探究直角三角形的性质,教师提问学生回答,同步擦除蒙层显示答案,归纳结论。
活动设计
运用蒙层功能遮挡答案。运用触发动画功能显示文本。
使用说明
∵四边形ABCD是矩形,
∴AC=BD.
OA= = AC,OB= = BD .
∴ OA= BD,OB= AC.
再探新知
直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
几何语言:∵在Rt△ABC中,OB是斜边AC的中线
3、在Rt△ABC 中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为 。
4.在直角三角形ABC中,两直角边分别为5和12,则斜边上的中线为 。
对到目前为止学过的直角三角形的性质加以总结
活动设计
运用思维导图功能进行总结
使用说明
总结归纳
如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分。
∴ OA = OB
又 ∵ ∠AOB=60°,
∴ ΔOAB是等边三角形
∴OA=AB=4(cm)
∴ AC=BD = 2OA=2×4=8(cm)
例题精析
A
B
C
D
O
回顾反思
1.矩形定义及性质
2.直角三角形斜边上的中线等于斜边一半
分层布置作业,让不同能力的学生有不同收获
活动设计
运用形状功能绘图
使用说明
作业
1.矩形ABCD的对角线AC =6cm,则另一条对角线BD=_______。
2.已知矩形ABCD,AC=8,则BD= ,OD= 。
3.已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 , , .
4.已知矩形的周长是24cm,相邻两边之比是 1:2,那么这个矩形
的边长分别是 ,对角线长是_________.
5.如图,已知矩形ABCD,AC=4,则BD= ,∠ABC= _ °
若∠ADB=30°,则∠AOD= °;∠COD= AB=____,AD=______.
6.矩形不一定具有的性质是( )
A、对角线相等 B、四个角相等 C、是轴对称图形 D、对角线互相垂直
A
B
C
D
O
7.求证:矩形的对角线相等
