18.2.1 矩形 第2课时 课件(共20张PPT)-八年级数学下册同步课件 练习(人教版)
文档属性
| 名称 | 18.2.1 矩形 第2课时 课件(共20张PPT)-八年级数学下册同步课件 练习(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 564.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 16:30:50 | ||
图片预览







文档简介
(共20张PPT)
第18.2.1 矩形第2课时
人教版数学八年级下册
1.理解矩形的判定定理.
2.尝试对矩形判定定理的证明.
3.利用矩形的判定定理解决简单问题.
学习目标
有一个角是直角的平行四边形是矩形,也就是长方形.
矩形:
矩形的性质:
1.对边平行且相等,
2.四个角都是直角,
3.对角线互相平分且相等.
复习引入
前面我们研究了矩形的性质,下面我们研究如何判定一个平行四边形或四边形是矩形.
由矩形的定义可知,有一个角是直角的平行四边形是矩形.
除此之外,还有没有其他判定方法呢
与研究平行四边形的方法类似,我们研究矩形的性质定理的逆命题,看看它们是否成立.
互动新授
思考
我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
1.对角线相等的平行四边形是矩形.
猜想:
你能证明上述猜想吗?
互动新授
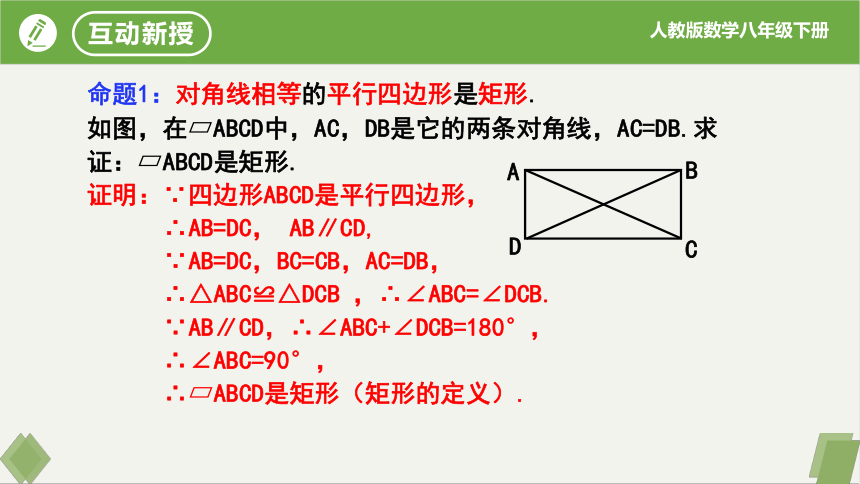
如图,在 ABCD中,AC,DB是它的两条对角线,AC=DB.求证: ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=DC, AB∥CD,
∵AB=DC,BC=CB,AC=DB,
∴△ABC≌△DCB ,∴∠ABC=∠DCB.
∵AB∥CD,∴∠ABC+∠DCB=180°,
∴∠ABC=90°,
∴ ABCD是矩形(矩形的定义).
A
B
C
D
命题1:对角线相等的平行四边形是矩形.
互动新授
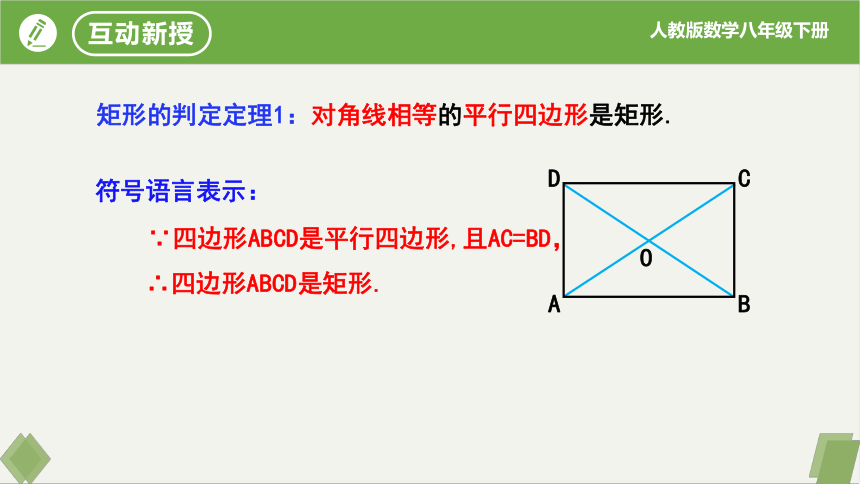
矩形的判定定理1:
D C
A B
O
符号语言表示:
∵四边形ABCD是平行四边形,且AC=BD,
∴四边形ABCD是矩形.
对角线相等的平行四边形是矩形.
互动新授
前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
根据四边形的内角和等于360°,由三个角是直角,可得出第四个角也是直角.
2.有三个角是直角的四边形是矩形.
猜想:
你能证明上述猜想吗?
互动新授
命题2:有三个角是直角的四边形是矩形.
如图,在四边形ABCD中,∠A=∠B=∠C=90°,求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
A
B
C
D
互动新授
矩形的判定定理2:
符号语言表示:
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
有三个角是直角的四边形是矩形.
A
B
C
D
互动新授
例1 如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,OB=OD= BD.
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
∵∠OAD=50°,
∴∠OAB=40°.
D C
A B
O
典例精析
1.如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90°
B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO
D.AO=BO=CO=DO
C
小试牛刀
2.如图,在 ABCD中,AC、BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是( )
A.∠BAC=∠ACB B.∠BAC=∠ACD
C.∠BAC=∠DAC D.∠BAC=∠ABD
D
小试牛刀
1.现在你能帮两个徒弟解决问题了吗?这两个徒弟下列判定所做的门为矩形的方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩形.( )
×
√
×
√
√
课堂检测
2.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=3,BC=4,AC=5.求证:四边形ABCD是矩形.
证明:四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°,
∵△ABC中,AB=3,BC=4,AC=5,
∵52=32+42,
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
课堂检测
1. 如图, ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:在 ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、∠ABC的平分线,
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴ ∠BAE+∠ABF= ∠DAB+ ∠ABC=90°.
A
B
D
C
H
E
F
G
拓展训练
1.有一个角是直角的平行四边形是矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
判定定理
课堂小结
1.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、∠MCA、∠ACN、∠CAF的角平分线,则四边形ABCD是( )
A.一般四边形 B.平行四边形
C.矩形 D.不能确定
C
课后作业
2.如图 ABCD中, ∠1=∠2中.此时四边形ABCD是矩形吗?为什么?
解:四边形ABCD是矩形.
理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
∵ ∠1= ∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD是矩形.
A
B
C
D
O
1
2
课后作业
谢谢聆听
第18.2.1 矩形第2课时
人教版数学八年级下册
1.理解矩形的判定定理.
2.尝试对矩形判定定理的证明.
3.利用矩形的判定定理解决简单问题.
学习目标
有一个角是直角的平行四边形是矩形,也就是长方形.
矩形:
矩形的性质:
1.对边平行且相等,
2.四个角都是直角,
3.对角线互相平分且相等.
复习引入
前面我们研究了矩形的性质,下面我们研究如何判定一个平行四边形或四边形是矩形.
由矩形的定义可知,有一个角是直角的平行四边形是矩形.
除此之外,还有没有其他判定方法呢
与研究平行四边形的方法类似,我们研究矩形的性质定理的逆命题,看看它们是否成立.
互动新授
思考
我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
1.对角线相等的平行四边形是矩形.
猜想:
你能证明上述猜想吗?
互动新授
如图,在 ABCD中,AC,DB是它的两条对角线,AC=DB.求证: ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=DC, AB∥CD,
∵AB=DC,BC=CB,AC=DB,
∴△ABC≌△DCB ,∴∠ABC=∠DCB.
∵AB∥CD,∴∠ABC+∠DCB=180°,
∴∠ABC=90°,
∴ ABCD是矩形(矩形的定义).
A
B
C
D
命题1:对角线相等的平行四边形是矩形.
互动新授
矩形的判定定理1:
D C
A B
O
符号语言表示:
∵四边形ABCD是平行四边形,且AC=BD,
∴四边形ABCD是矩形.
对角线相等的平行四边形是矩形.
互动新授
前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
根据四边形的内角和等于360°,由三个角是直角,可得出第四个角也是直角.
2.有三个角是直角的四边形是矩形.
猜想:
你能证明上述猜想吗?
互动新授
命题2:有三个角是直角的四边形是矩形.
如图,在四边形ABCD中,∠A=∠B=∠C=90°,求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
A
B
C
D
互动新授
矩形的判定定理2:
符号语言表示:
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
有三个角是直角的四边形是矩形.
A
B
C
D
互动新授
例1 如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,OB=OD= BD.
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
∵∠OAD=50°,
∴∠OAB=40°.
D C
A B
O
典例精析
1.如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90°
B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO
D.AO=BO=CO=DO
C
小试牛刀
2.如图,在 ABCD中,AC、BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是( )
A.∠BAC=∠ACB B.∠BAC=∠ACD
C.∠BAC=∠DAC D.∠BAC=∠ABD
D
小试牛刀
1.现在你能帮两个徒弟解决问题了吗?这两个徒弟下列判定所做的门为矩形的方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩形.( )
×
√
×
√
√
课堂检测
2.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=3,BC=4,AC=5.求证:四边形ABCD是矩形.
证明:四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°,
∵△ABC中,AB=3,BC=4,AC=5,
∵52=32+42,
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
课堂检测
1. 如图, ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:在 ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、∠ABC的平分线,
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴ ∠BAE+∠ABF= ∠DAB+ ∠ABC=90°.
A
B
D
C
H
E
F
G
拓展训练
1.有一个角是直角的平行四边形是矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
判定定理
课堂小结
1.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、∠MCA、∠ACN、∠CAF的角平分线,则四边形ABCD是( )
A.一般四边形 B.平行四边形
C.矩形 D.不能确定
C
课后作业
2.如图 ABCD中, ∠1=∠2中.此时四边形ABCD是矩形吗?为什么?
解:四边形ABCD是矩形.
理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
∵ ∠1= ∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD是矩形.
A
B
C
D
O
1
2
课后作业
谢谢聆听
