18.2.2 菱形 第2课时 课件(共21张PPT)-八年级数学下册同步课件 练习(人教版)
文档属性
| 名称 | 18.2.2 菱形 第2课时 课件(共21张PPT)-八年级数学下册同步课件 练习(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 649.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 16:36:08 | ||
图片预览






文档简介
(共21张PPT)
第18.2.2 菱形第2课时
人教版数学八年级下册
1.理解菱形的判定定理.
2.尝试对菱形判定定理的证明.
3.利用菱形的判定定理解决简单问题.
学习目标
菱形:
有一组邻边相等的平行四边形是菱形.
菱形的性质:
1.对边平行,
2.对角相等,
3.菱形的四条边都相等,
4.对角线互相平分且垂直,并且每一条对角线平分一组对角.
5.菱形是轴对称图形,它的对角线所在的直线就是它的对称轴.
= 底×高 = 对角线乘积的一半
菱形的面积
复习引入
前面我们研究了菱形的性质,下面我们研究如何判定一个平行四边形或四边形是菱形.
由菱形的定义可知,有一组邻边相等的平行四边形是菱形.
除此之外,还有没有其他判定方法呢
与研究平行四边形、矩形的方法类似,我们研究菱形的性质定理的逆命题,看看它们是否成立.
互动新授
思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
猜想1:
你能证明上述猜想吗?
对角线互相垂直的平行四边形是菱形.
互动新授
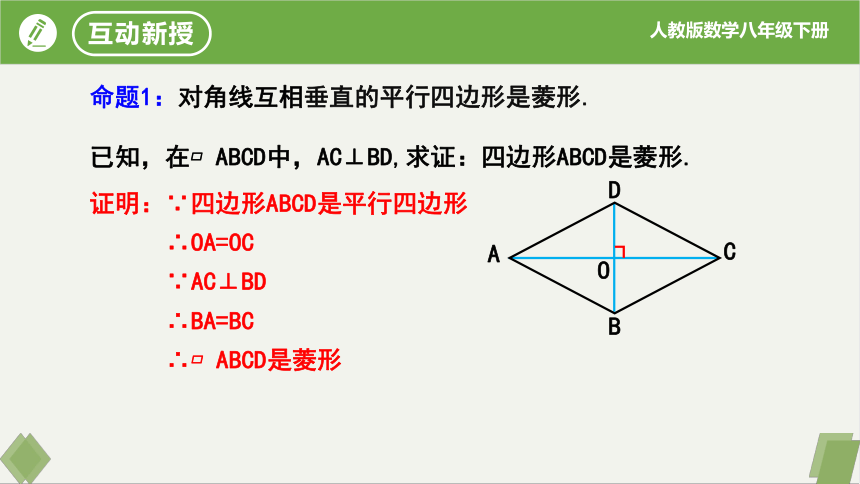
命题1:对角线互相垂直的平行四边形是菱形.
证明:∵四边形ABCD是平行四边形
∴OA=OC
∵AC⊥BD
∴BA=BC
∴ ABCD是菱形
已知,在 ABCD中,AC⊥BD,求证:四边形ABCD是菱形.
A
B
C
O
D
互动新授
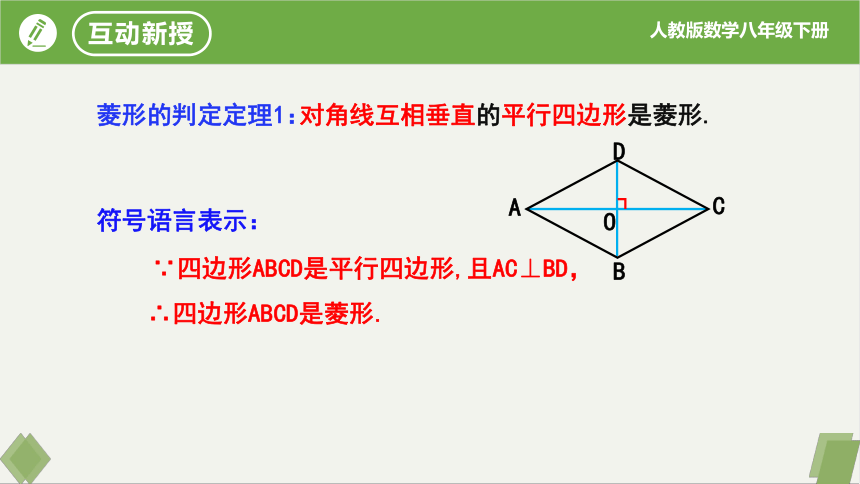
菱形的判定定理1:
符号语言表示:
∵四边形ABCD是平行四边形,且AC⊥BD,
∴四边形ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
A
B
C
O
D
互动新授
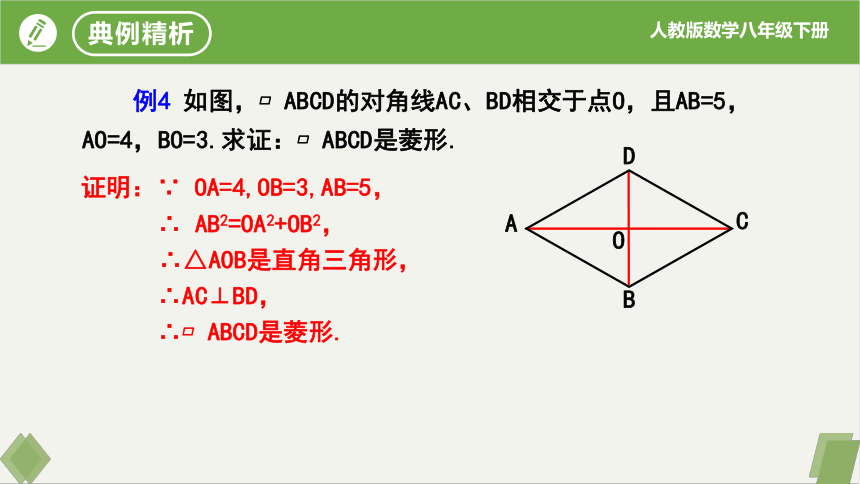
例4 如图, ABCD的对角线AC、BD相交于点O,且AB=5,AO=4,BO=3.求证: ABCD是菱形.
证明:∵ OA=4,OB=3,AB=5,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴AC⊥BD,
∴ ABCD是菱形.
A
B
C
O
D
典例精析
思考
我们知道,菱形的四条边相等.反过来,四条边相等的四边形是菱形吗?
猜想2:
你能证明上述猜想吗?
四条边相等的四边形是菱形.
互动新授
命题2:四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=AD,求证:四边形ABCD是菱形.
A
B
C
D
证明:∵AD=BC,AB=CD
∴四边形ABCD是平行四边形
∵AB=AD
∴四边形ABCD是菱形
互动新授
菱形的判定定理2:
符号语言表示:
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
A
B
C
D
四条边相等的四边形是菱形.
互动新授
1.已知四边形ABCD是平行四边形,下列结论中正确的有( )
①当AB=BC时,四边形ABCD是菱形;
②当AC⊥BD时,四边形ABCD是菱形;
③当∠ABC=90°时,四边形ABCD是菱形:
④当AC=BD时,四边形ABCD是菱形;
A.3个 B.4个 C.1个 D.2个
D
小试牛刀
2.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
C
小试牛刀
1.如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
A.∠1=∠2 B.BE=DF
C.∠EDF=60° D.AB=AF
B
课堂检测
证明:∵∠1=∠2且AE=AC,AD=AD,
∴△ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
2.如图,在△ABC中, AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF = ED.求证:四边形CDEF是菱形.
课堂检测
1.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
∵EF=BE,
∴四边形BCFE是菱形;
拓展训练
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
拓展训练
菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.
A
B
C
O
D
菱形的判定定理2:
四条边相等的四边形是菱形.
符号语言表示:
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
符号语言表示:
∵四边形ABCD是平行四边形,且AC⊥BD,
∴四边形ABCD是菱形.
课堂小结
1.判断
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
√
╳
╳
╳
课后作业
2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形
证明:∵DE∥AC, CE∥BD
∴四边形OCED是平行四边形
∵四边形ABCD是矩形
∴OC=OD
∴四边形OCED是菱形(一组邻边相等的平行四边形是菱形)
A
B
C
D
O
E
课后作业
谢谢聆听
第18.2.2 菱形第2课时
人教版数学八年级下册
1.理解菱形的判定定理.
2.尝试对菱形判定定理的证明.
3.利用菱形的判定定理解决简单问题.
学习目标
菱形:
有一组邻边相等的平行四边形是菱形.
菱形的性质:
1.对边平行,
2.对角相等,
3.菱形的四条边都相等,
4.对角线互相平分且垂直,并且每一条对角线平分一组对角.
5.菱形是轴对称图形,它的对角线所在的直线就是它的对称轴.
= 底×高 = 对角线乘积的一半
菱形的面积
复习引入
前面我们研究了菱形的性质,下面我们研究如何判定一个平行四边形或四边形是菱形.
由菱形的定义可知,有一组邻边相等的平行四边形是菱形.
除此之外,还有没有其他判定方法呢
与研究平行四边形、矩形的方法类似,我们研究菱形的性质定理的逆命题,看看它们是否成立.
互动新授
思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
猜想1:
你能证明上述猜想吗?
对角线互相垂直的平行四边形是菱形.
互动新授
命题1:对角线互相垂直的平行四边形是菱形.
证明:∵四边形ABCD是平行四边形
∴OA=OC
∵AC⊥BD
∴BA=BC
∴ ABCD是菱形
已知,在 ABCD中,AC⊥BD,求证:四边形ABCD是菱形.
A
B
C
O
D
互动新授
菱形的判定定理1:
符号语言表示:
∵四边形ABCD是平行四边形,且AC⊥BD,
∴四边形ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
A
B
C
O
D
互动新授
例4 如图, ABCD的对角线AC、BD相交于点O,且AB=5,AO=4,BO=3.求证: ABCD是菱形.
证明:∵ OA=4,OB=3,AB=5,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴AC⊥BD,
∴ ABCD是菱形.
A
B
C
O
D
典例精析
思考
我们知道,菱形的四条边相等.反过来,四条边相等的四边形是菱形吗?
猜想2:
你能证明上述猜想吗?
四条边相等的四边形是菱形.
互动新授
命题2:四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=AD,求证:四边形ABCD是菱形.
A
B
C
D
证明:∵AD=BC,AB=CD
∴四边形ABCD是平行四边形
∵AB=AD
∴四边形ABCD是菱形
互动新授
菱形的判定定理2:
符号语言表示:
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
A
B
C
D
四条边相等的四边形是菱形.
互动新授
1.已知四边形ABCD是平行四边形,下列结论中正确的有( )
①当AB=BC时,四边形ABCD是菱形;
②当AC⊥BD时,四边形ABCD是菱形;
③当∠ABC=90°时,四边形ABCD是菱形:
④当AC=BD时,四边形ABCD是菱形;
A.3个 B.4个 C.1个 D.2个
D
小试牛刀
2.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
C
小试牛刀
1.如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
A.∠1=∠2 B.BE=DF
C.∠EDF=60° D.AB=AF
B
课堂检测
证明:∵∠1=∠2且AE=AC,AD=AD,
∴△ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
2.如图,在△ABC中, AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF = ED.求证:四边形CDEF是菱形.
课堂检测
1.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
∵EF=BE,
∴四边形BCFE是菱形;
拓展训练
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
拓展训练
菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.
A
B
C
O
D
菱形的判定定理2:
四条边相等的四边形是菱形.
符号语言表示:
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
符号语言表示:
∵四边形ABCD是平行四边形,且AC⊥BD,
∴四边形ABCD是菱形.
课堂小结
1.判断
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
√
╳
╳
╳
课后作业
2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形
证明:∵DE∥AC, CE∥BD
∴四边形OCED是平行四边形
∵四边形ABCD是矩形
∴OC=OD
∴四边形OCED是菱形(一组邻边相等的平行四边形是菱形)
A
B
C
D
O
E
课后作业
谢谢聆听
