18.2.2.2 菱形的判定 课件(共23张PPT)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 18.2.2.2 菱形的判定 课件(共23张PPT)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 16:35:06 | ||
图片预览




文档简介
(共23张PPT)
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.2.2.2
菱形的判定
复习引入
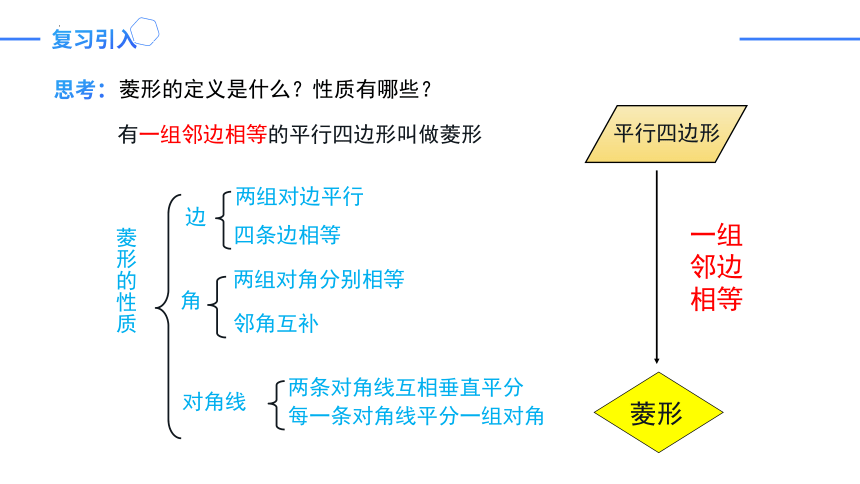
菱形的定义是什么?性质有哪些?
一组
邻边
相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
两条对角线互相垂直平分
每一条对角线平分一组对角
边
角
对角线
思考:
菱形的判定1
新知探究
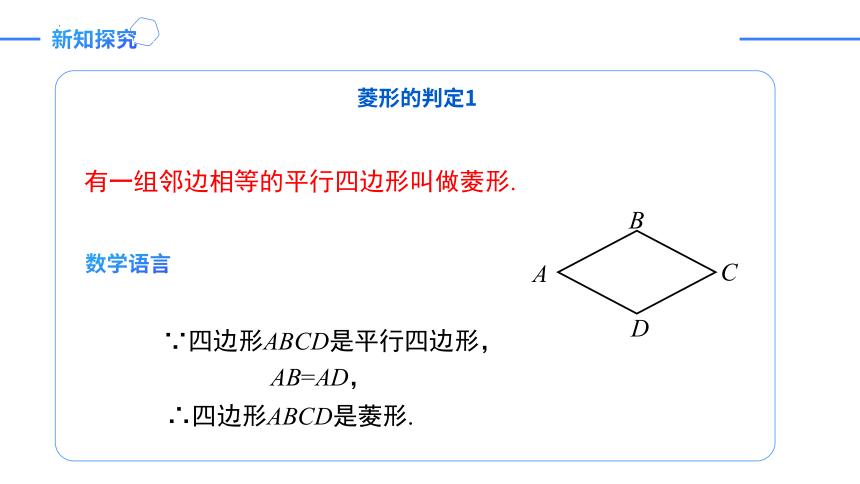
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
数学语言
有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
新知探究
思考:
用 4 支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:
四条边都相等的四边形是菱形吗?
你能写出该命题的“已知”和“求证”吗?
尝试证明之.
新知探究
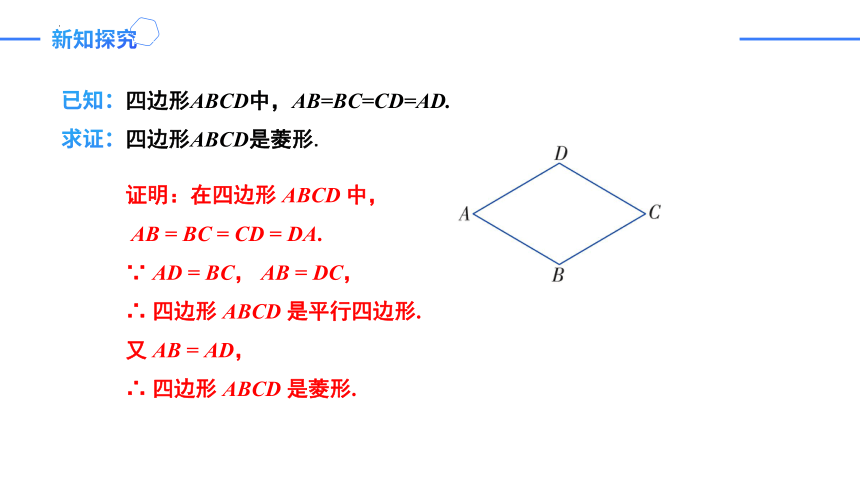
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:在四边形 ABCD 中,
AB = BC = CD = DA.
∵ AD = BC, AB = DC,
∴ 四边形 ABCD 是平行四边形.
又 AB = AD,
∴ 四边形 ABCD 是菱形.
菱形的判定2
新知探究
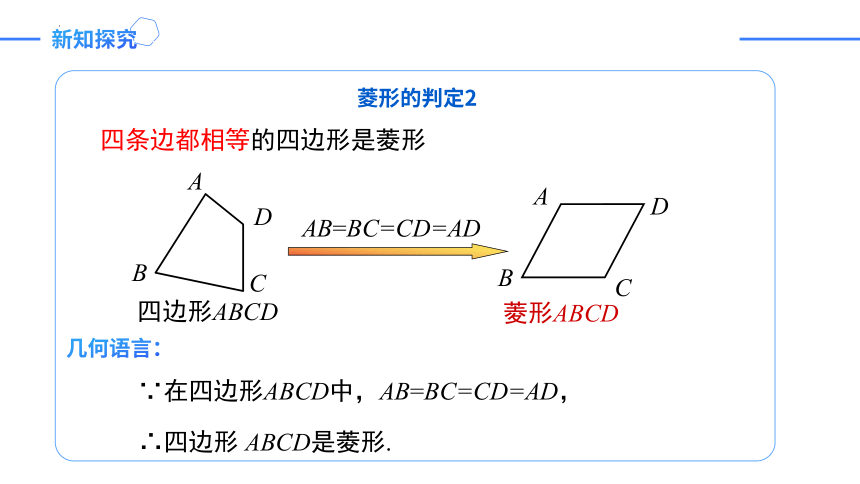
四条边都相等的四边形是菱形
AB=BC=CD=AD
几何语言:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
典例精析
例1
已知:如图,在四边形 ABCD 中,线段 BD垂直平分 AC,且相交于点 O,∠1 =∠2.求证:四边形 ABCD 是菱形.
证明 ∵线段 BD 垂直平分AC ,
∴ BA = BC,DA = DC,OA = OC.
在△AOB 和△COD 中,
∵∠1 =∠2,∠AOB =∠COD,OA = OC.
∴△OAB≌△OCD. ∴ AB = CD.
∴BA = BC = CD = DA.
∴四边形 ABCD 是菱形(四条边都相等的四边形是菱形).
新知探究
思考:
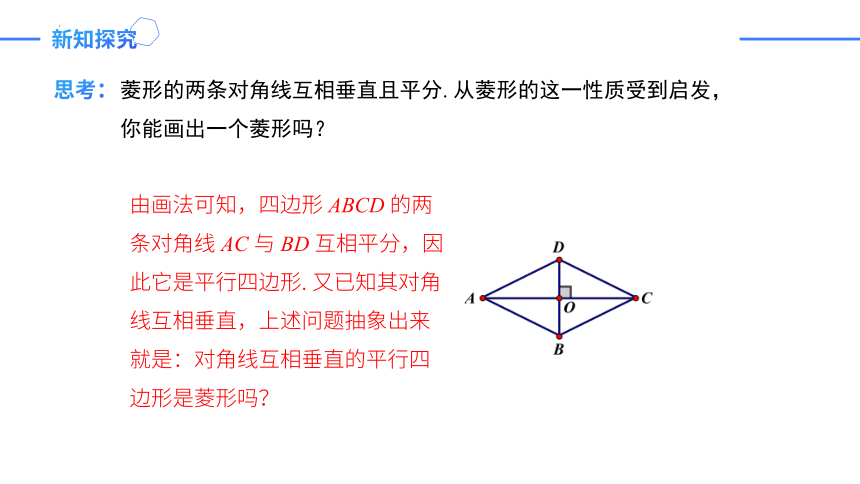
菱形的两条对角线互相垂直且平分. 从菱形的这一性质受到启发,你能画出一个菱形吗?
由画法可知,四边形 ABCD 的两条对角线 AC 与 BD 互相平分,因此它是平行四边形. 又已知其对角线互相垂直,上述问题抽象出来就是:对角线互相垂直的平行四边形是菱形吗?
新知探究
思考:
菱形的两条对角线互相垂直且平分. 从菱形的这一性质受到启发,你能画出一个菱形吗?
证明:
∵ 在 □ ABCD中,AC⊥BD,OA= OC,
∴BD 所在的直线是 AC 的垂直平分线.
∴ DA= DC.
∴ □ ABCD 是菱形.
菱形的判定3
新知探究
对角线互相垂直的平行四边形是菱形
AC⊥BD
几何语言:
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
典例精析
例2
证明:在Rt△BON和Rt△DOM 中,
∵ BO = DO, ∠DBN = ∠BDM,
∴ Rt△BON≌Rt△DOM. ∴OM=ON.
∵BD,NM 是四边形 BNDM的两条对角线且互相平分,
∴四边形 BNDM 是平行四边形.
又 MN⊥BD, ∴四边形 BNDM 是菱形.
如图,在平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,过点 O 作 MN⊥BD,分别交 AD,BC 于点M,N .
求证:四边形 BNDM 是菱形.
典例精析
例3
已知:如图,在 ABCD中,对角线AC与BD相交于点O,
AB = ,OA=2,OB=1. 求证: ABCD是菱形.
证明:在△AOB中,
∵AB= ,OA=2,OB=1,
∴AB2=AO2+OB2.
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD.
∴ ABCD是菱形(对角线垂直的平行四边形是菱形).
典例精析
例4
在学平行四边形的时候我们知道把两张等宽的纸条交叉重叠在一起得到的四边形是平行四边形,你能进一步判断重叠部分ABCD的形状吗?
A
C
D
B
分析:易知四边形ABCD是平行四边形,
只需证一组邻边相等或对角线互相垂直
即可进一步判断.
由题意可知BC边上的高和CD边上的高相等,
然后通过证△ABE≌△ADF,即得AB=AD.
E
F
归纳总结
典例精析
1.菱形的判定方法:
(1)(定义法):一组邻边相等的平行四边形是菱形;
(2)(对角线):对角线互相垂直的平行四边形是菱形;
(3)(边):四边相等的四边形是菱形.
平行四边形
四边形
2.判定菱形的常见思路:
四条边都相等
判定条件
对角线互相垂直
一组邻边相等
菱形
典例精析
例5
(1)证明:由尺规作∠BAF的平分线的过程
可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
典例精析
例5
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.
归纳总结
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四边相等的四边形是菱形.
运用定理进行计算和证明
菱形的判定
定义法
判定定理
归纳总结
1.下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形 B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形 D.四个角相等的四边形是菱形
C
2.能判定一个四边形是菱形的条件是( )
A.对角线相等且互相垂直
B.对角线相等且互相平分
C.对角线互相垂直
D.对角线互相垂直平分
D
当堂检测
3.如图,在□ ABCD 中, 对角线 AC, BD相交于点 O, 添加下列条件不能判定 □ ABCD 是菱形的是( )
A. AC⊥BD B. AB=BC
C. AC=BD D. ∠1=∠2
C
4.如图,在 ABCD中,AC,BD交于点O,AB=13,AC=24,DB=10,则四边形ABCD是 ( )
A.一般的平行四边形 B.长方形
C.菱形 D.不能确定
C
当堂检测
解:四边形 ABCD是菱形. 理由如下:
∵△ABC 为等腰三角形,∴AB=BC.
∵△CDA为等腰三角形,∴CD=AD.
而△CDA是△ABC的像,∴AB=BC=CD=DA.
∴四边形 ABCD 是菱形.
5.如图,把等腰三角形 ABC 绕它的底边 AC 上的中点 O 旋转180°,得到三角形 CDA,试问: 四边形 ABCD 是菱形吗?为什么?
当堂检测
6.如图,矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明:∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.
当堂检测
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形CDEF是菱形.
2
7.如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,
EF = ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.2.2.2
菱形的判定
复习引入
菱形的定义是什么?性质有哪些?
一组
邻边
相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
两条对角线互相垂直平分
每一条对角线平分一组对角
边
角
对角线
思考:
菱形的判定1
新知探究
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
数学语言
有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
新知探究
思考:
用 4 支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:
四条边都相等的四边形是菱形吗?
你能写出该命题的“已知”和“求证”吗?
尝试证明之.
新知探究
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:在四边形 ABCD 中,
AB = BC = CD = DA.
∵ AD = BC, AB = DC,
∴ 四边形 ABCD 是平行四边形.
又 AB = AD,
∴ 四边形 ABCD 是菱形.
菱形的判定2
新知探究
四条边都相等的四边形是菱形
AB=BC=CD=AD
几何语言:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
典例精析
例1
已知:如图,在四边形 ABCD 中,线段 BD垂直平分 AC,且相交于点 O,∠1 =∠2.求证:四边形 ABCD 是菱形.
证明 ∵线段 BD 垂直平分AC ,
∴ BA = BC,DA = DC,OA = OC.
在△AOB 和△COD 中,
∵∠1 =∠2,∠AOB =∠COD,OA = OC.
∴△OAB≌△OCD. ∴ AB = CD.
∴BA = BC = CD = DA.
∴四边形 ABCD 是菱形(四条边都相等的四边形是菱形).
新知探究
思考:
菱形的两条对角线互相垂直且平分. 从菱形的这一性质受到启发,你能画出一个菱形吗?
由画法可知,四边形 ABCD 的两条对角线 AC 与 BD 互相平分,因此它是平行四边形. 又已知其对角线互相垂直,上述问题抽象出来就是:对角线互相垂直的平行四边形是菱形吗?
新知探究
思考:
菱形的两条对角线互相垂直且平分. 从菱形的这一性质受到启发,你能画出一个菱形吗?
证明:
∵ 在 □ ABCD中,AC⊥BD,OA= OC,
∴BD 所在的直线是 AC 的垂直平分线.
∴ DA= DC.
∴ □ ABCD 是菱形.
菱形的判定3
新知探究
对角线互相垂直的平行四边形是菱形
AC⊥BD
几何语言:
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
典例精析
例2
证明:在Rt△BON和Rt△DOM 中,
∵ BO = DO, ∠DBN = ∠BDM,
∴ Rt△BON≌Rt△DOM. ∴OM=ON.
∵BD,NM 是四边形 BNDM的两条对角线且互相平分,
∴四边形 BNDM 是平行四边形.
又 MN⊥BD, ∴四边形 BNDM 是菱形.
如图,在平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,过点 O 作 MN⊥BD,分别交 AD,BC 于点M,N .
求证:四边形 BNDM 是菱形.
典例精析
例3
已知:如图,在 ABCD中,对角线AC与BD相交于点O,
AB = ,OA=2,OB=1. 求证: ABCD是菱形.
证明:在△AOB中,
∵AB= ,OA=2,OB=1,
∴AB2=AO2+OB2.
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD.
∴ ABCD是菱形(对角线垂直的平行四边形是菱形).
典例精析
例4
在学平行四边形的时候我们知道把两张等宽的纸条交叉重叠在一起得到的四边形是平行四边形,你能进一步判断重叠部分ABCD的形状吗?
A
C
D
B
分析:易知四边形ABCD是平行四边形,
只需证一组邻边相等或对角线互相垂直
即可进一步判断.
由题意可知BC边上的高和CD边上的高相等,
然后通过证△ABE≌△ADF,即得AB=AD.
E
F
归纳总结
典例精析
1.菱形的判定方法:
(1)(定义法):一组邻边相等的平行四边形是菱形;
(2)(对角线):对角线互相垂直的平行四边形是菱形;
(3)(边):四边相等的四边形是菱形.
平行四边形
四边形
2.判定菱形的常见思路:
四条边都相等
判定条件
对角线互相垂直
一组邻边相等
菱形
典例精析
例5
(1)证明:由尺规作∠BAF的平分线的过程
可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
典例精析
例5
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.
归纳总结
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四边相等的四边形是菱形.
运用定理进行计算和证明
菱形的判定
定义法
判定定理
归纳总结
1.下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形 B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形 D.四个角相等的四边形是菱形
C
2.能判定一个四边形是菱形的条件是( )
A.对角线相等且互相垂直
B.对角线相等且互相平分
C.对角线互相垂直
D.对角线互相垂直平分
D
当堂检测
3.如图,在□ ABCD 中, 对角线 AC, BD相交于点 O, 添加下列条件不能判定 □ ABCD 是菱形的是( )
A. AC⊥BD B. AB=BC
C. AC=BD D. ∠1=∠2
C
4.如图,在 ABCD中,AC,BD交于点O,AB=13,AC=24,DB=10,则四边形ABCD是 ( )
A.一般的平行四边形 B.长方形
C.菱形 D.不能确定
C
当堂检测
解:四边形 ABCD是菱形. 理由如下:
∵△ABC 为等腰三角形,∴AB=BC.
∵△CDA为等腰三角形,∴CD=AD.
而△CDA是△ABC的像,∴AB=BC=CD=DA.
∴四边形 ABCD 是菱形.
5.如图,把等腰三角形 ABC 绕它的底边 AC 上的中点 O 旋转180°,得到三角形 CDA,试问: 四边形 ABCD 是菱形吗?为什么?
当堂检测
6.如图,矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明:∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.
当堂检测
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形CDEF是菱形.
2
7.如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,
EF = ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
