18.2.3.1 正方形的性质 课件(共24张PPT)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 18.2.3.1 正方形的性质 课件(共24张PPT)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 16:39:36 | ||
图片预览




文档简介
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.2.3.1
正方形的性质
情景引入
这样的图形生活中无处不在!它们都有什么特点呢?
情景引入
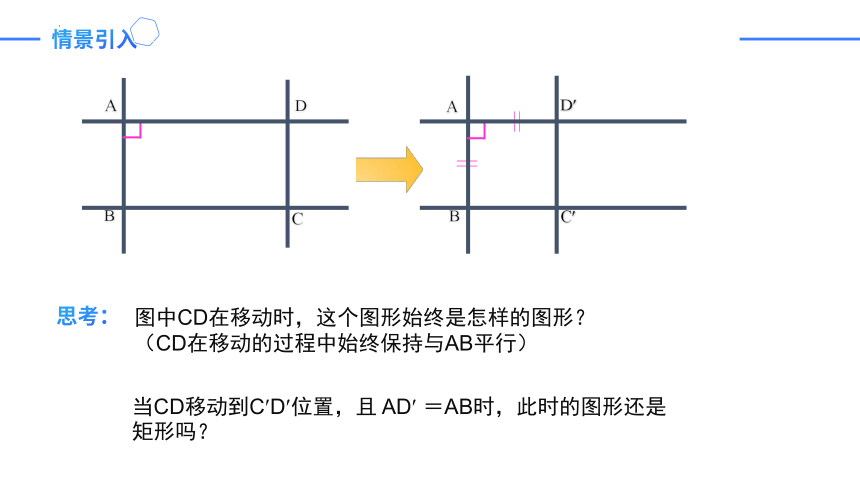
图中CD在移动时,这个图形始终是怎样的图形?
(CD在移动的过程中始终保持与AB平行)
当CD移动到C?D?位置,且 AD? =AB时,此时的图形还是矩形吗?
A
B
C
D
A
B
C?
D?
思考:
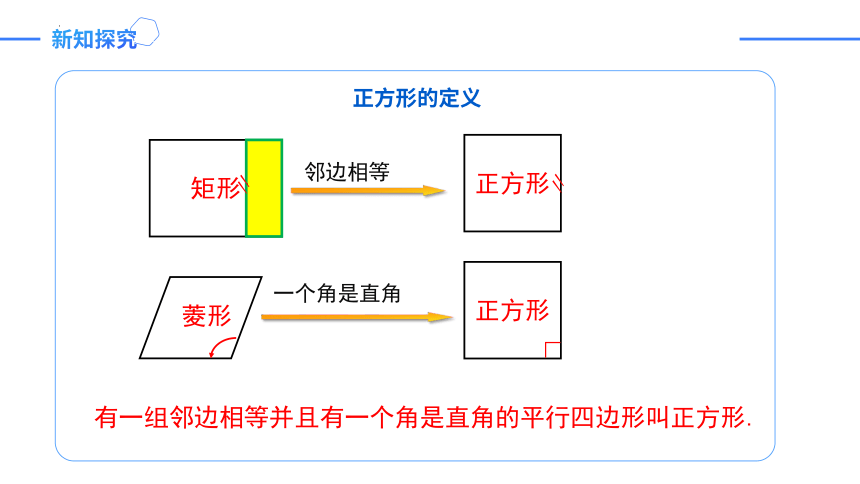
正方形的定义
新知探究
邻边相等
矩形
〃
正方形
〃
菱形
一个角是直角
正方形
∟
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
新知探究
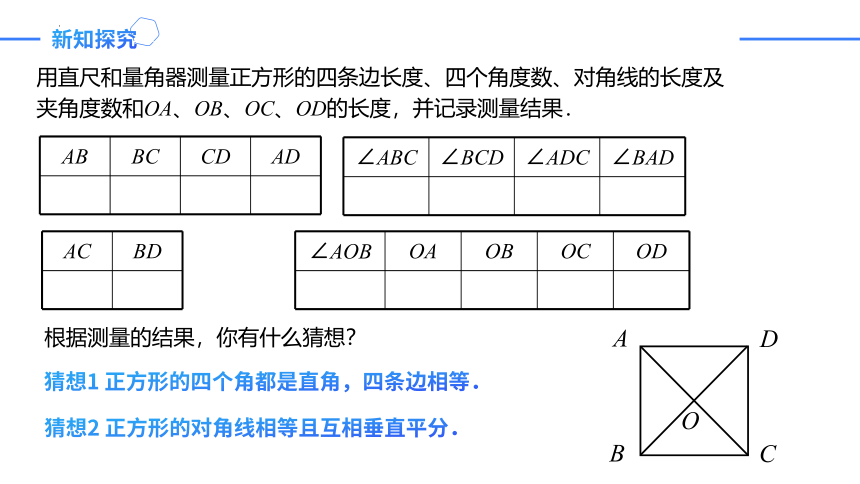
用直尺和量角器测量正方形的四条边长度、四个角度数、对角线的长度及夹角度数和OA、OB、OC、OD的长度,并记录测量结果.
A
B
C
D
O
AB
BC
CD
AD
根据测量的结果,你有什么猜想?
猜想1 正方形的四个角都是直角,四条边相等.
猜想2 正方形的对角线相等且互相垂直平分.
∠ABC
∠BCD
∠ADC
∠BAD
AC
BD
∠AOB
OA
OB
OC
OD
新知探究
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
新知探究
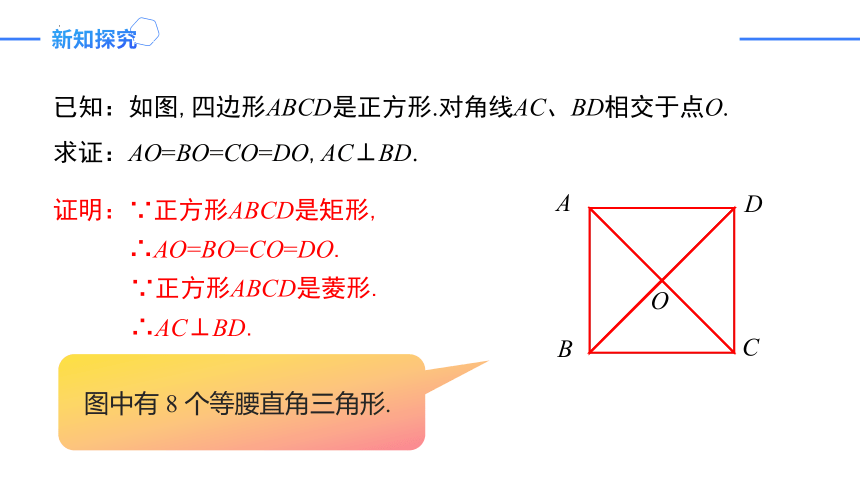
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
图中有 8 个等腰直角三角形.
A
B
C
D
O
新知探究
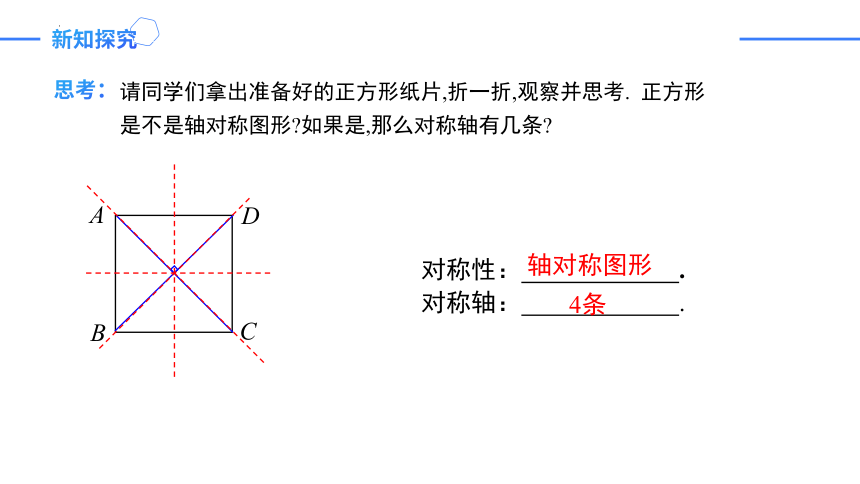
思考:
请同学们拿出准备好的正方形纸片,折一折,观察并思考.??正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
新知探究
正方形的特征:
1.具有平行四边形的一切特征
两组对边平行且相等,
两组对角相等,对角线互相平分
2.具有矩形的一切特征
四个角都是直角,对角线相等
3.具有菱形的一切特征
四条边都相等,对角线互相垂直且分别平分
4.既是中心对称图形,又是轴对称图形,有四条对称轴
O
A
B
C
D
平行四边形
四边形
正
方
形
矩形
菱形
平行四边形、菱形、矩形、正方形之间的关系
新知探究
矩形
正方形
平行四边形
菱形
一组邻边相等
一组邻边相等
一个角为直角
一个角为直角
典例精析
例1
在下列图中,有多少个正方形?有多少个矩形?
(1)
(2)
解:(1)有5个正方形,9个矩形;
(2)有14个正方形,36个矩形.
典例精析
例2
已知正方形ABCD的边AB长2cm,求这个正方形的周长、对角线长和它的面积.
解:①这个正方形的周长=4AB=4×2=8cm;
②这个正方形的对角线长= cm (勾股定理);
③这个正方形的面积=AB×AB=2×2=4(平方厘米)
典例精析
如图,在正方形 ABCD 中,点 F 为对角线 AC 上一点,连接 BF,DF. 你能找出图中的全等三角形吗?选择其中一对进行证明.
A
B
F
D
C
全等三角形有:△ AFD ≌ △AFB,
△CFD ≌ △CFB,△ACD ≌ △ABD.
例3
证明:∵四边形 ABCD 为正方形,
∴AD = AB ( 正方形的四条边都相等 ).
∠DAF =∠BAF
在 △ AFD 和 △AFB 中
∵ AF = AF,
∠DAF = ∠BAF,
AD = AB,
∴△ AFD ≌ △AFB ( SAS ).
典例精析
例4
如图四边形ABCD和DEFG都是正方形,试说明AE=CG
解:
因为四边形ABCD是正方形
根据正方形的四边相等,得
AD=CD
又知四边形DEFG也是正方形
所以 DE=DG
又因为正方形的每个内角为90°
所以∠ADE+∠EDC=∠CDG+∠EDC
所以∠ADE=∠CDG
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。
所以AE=CG
A
B
C
D
E
F
G
典例精析
例5
如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC
∵PE⊥BC , PF⊥DC
而四边形ABCD是正方形
∴∠FCE=90°
∴四边形PECF是矩形
∴PC=EF
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=EF
典例精析
例6
如图,已知正方形ABCD的边长为1,连接AC,BD相交于点O,CE平分∠ACD交BD于点E,求DE的长.
A
B
C
D
O
E
F
解:过点E作EF⊥CD于F.
∵四边形ABCD是正方形,
∴AC⊥BD,∠BDC=45°,
∴∠EDF=45°,
∴EF=DF.
∵CE平分∠ACD交BD于点E,
∴EO=EF.
又∵∠EOC=∠EFC=90°,
EC=EC,
∴Rt△CEO≌Rt△CEF.
典例精析
例7
如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,求∠EAF的度数.
解:在Rt△ABF与Rt△AGF中,
∵AB=AG,AF=AF,∠B=∠AGF=90°,
∴△ABF≌△AGF(HL),∴∠BAF=∠GAF,
同理易得:△AGE≌△ADE,有∠GAE=∠DAE;
即∠EAF=∠EAG+∠FAG=12(∠DAG+∠BAG)
=12∠DAB=45°,
故∠EAF=45°.
?
归纳总结
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
正方形与平行四边形、矩形、菱形的关系
当堂检测
随堂练习
1.平行四边形、矩形、菱形、正方形都具有的性质是 ( )
A.对角线互相平分 B.对角线相互垂直
C.对角线相等 D.对角线互相垂直平分且相等
2.如图,在菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的周长为 ( )
A.14 B.15 C.12 D.17
A
C
A
B
C
D
E
F
60°
当堂检测
45°
正方形
12cm
2a+1
3.正方形的一边和对角线的夹角为___________.
4.如果一个四边形既是菱形又是矩形,那么它一定是_________.
5.已知正方形的面积为9cm?,它的周长为 _______________.
6.正方形的边长为a,当边长增加1时,其面积增加了__________.
O
A
B
C
D
7. 已知正方形ABCD在直角坐标系内,点A的坐标为(0,1),
点B的坐标为(0,0),则点C,D的坐标分别为________
和________.(只写一组)
8. 如图,在正方形ABCD中,E是对角线AC上一点,
且AE=AB,则∠EBC的度数是 .
A
D
B
C
O
E
(1,0)
(1,1)
22.5°
当堂检测
11.正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
9.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
30°
16cm
10.以正方形ABCD的边DC向外作等边△DCE,则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
M
A
B
C
D
E
F
O
当堂检测
12.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,
面积为AD2=8.
当堂检测
13.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC , PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.2.3.1
正方形的性质
情景引入
这样的图形生活中无处不在!它们都有什么特点呢?
情景引入
图中CD在移动时,这个图形始终是怎样的图形?
(CD在移动的过程中始终保持与AB平行)
当CD移动到C?D?位置,且 AD? =AB时,此时的图形还是矩形吗?
A
B
C
D
A
B
C?
D?
思考:
正方形的定义
新知探究
邻边相等
矩形
〃
正方形
〃
菱形
一个角是直角
正方形
∟
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
新知探究
用直尺和量角器测量正方形的四条边长度、四个角度数、对角线的长度及夹角度数和OA、OB、OC、OD的长度,并记录测量结果.
A
B
C
D
O
AB
BC
CD
AD
根据测量的结果,你有什么猜想?
猜想1 正方形的四个角都是直角,四条边相等.
猜想2 正方形的对角线相等且互相垂直平分.
∠ABC
∠BCD
∠ADC
∠BAD
AC
BD
∠AOB
OA
OB
OC
OD
新知探究
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
新知探究
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
图中有 8 个等腰直角三角形.
A
B
C
D
O
新知探究
思考:
请同学们拿出准备好的正方形纸片,折一折,观察并思考.??正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
新知探究
正方形的特征:
1.具有平行四边形的一切特征
两组对边平行且相等,
两组对角相等,对角线互相平分
2.具有矩形的一切特征
四个角都是直角,对角线相等
3.具有菱形的一切特征
四条边都相等,对角线互相垂直且分别平分
4.既是中心对称图形,又是轴对称图形,有四条对称轴
O
A
B
C
D
平行四边形
四边形
正
方
形
矩形
菱形
平行四边形、菱形、矩形、正方形之间的关系
新知探究
矩形
正方形
平行四边形
菱形
一组邻边相等
一组邻边相等
一个角为直角
一个角为直角
典例精析
例1
在下列图中,有多少个正方形?有多少个矩形?
(1)
(2)
解:(1)有5个正方形,9个矩形;
(2)有14个正方形,36个矩形.
典例精析
例2
已知正方形ABCD的边AB长2cm,求这个正方形的周长、对角线长和它的面积.
解:①这个正方形的周长=4AB=4×2=8cm;
②这个正方形的对角线长= cm (勾股定理);
③这个正方形的面积=AB×AB=2×2=4(平方厘米)
典例精析
如图,在正方形 ABCD 中,点 F 为对角线 AC 上一点,连接 BF,DF. 你能找出图中的全等三角形吗?选择其中一对进行证明.
A
B
F
D
C
全等三角形有:△ AFD ≌ △AFB,
△CFD ≌ △CFB,△ACD ≌ △ABD.
例3
证明:∵四边形 ABCD 为正方形,
∴AD = AB ( 正方形的四条边都相等 ).
∠DAF =∠BAF
在 △ AFD 和 △AFB 中
∵ AF = AF,
∠DAF = ∠BAF,
AD = AB,
∴△ AFD ≌ △AFB ( SAS ).
典例精析
例4
如图四边形ABCD和DEFG都是正方形,试说明AE=CG
解:
因为四边形ABCD是正方形
根据正方形的四边相等,得
AD=CD
又知四边形DEFG也是正方形
所以 DE=DG
又因为正方形的每个内角为90°
所以∠ADE+∠EDC=∠CDG+∠EDC
所以∠ADE=∠CDG
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。
所以AE=CG
A
B
C
D
E
F
G
典例精析
例5
如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC
∵PE⊥BC , PF⊥DC
而四边形ABCD是正方形
∴∠FCE=90°
∴四边形PECF是矩形
∴PC=EF
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=EF
典例精析
例6
如图,已知正方形ABCD的边长为1,连接AC,BD相交于点O,CE平分∠ACD交BD于点E,求DE的长.
A
B
C
D
O
E
F
解:过点E作EF⊥CD于F.
∵四边形ABCD是正方形,
∴AC⊥BD,∠BDC=45°,
∴∠EDF=45°,
∴EF=DF.
∵CE平分∠ACD交BD于点E,
∴EO=EF.
又∵∠EOC=∠EFC=90°,
EC=EC,
∴Rt△CEO≌Rt△CEF.
典例精析
例7
如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,求∠EAF的度数.
解:在Rt△ABF与Rt△AGF中,
∵AB=AG,AF=AF,∠B=∠AGF=90°,
∴△ABF≌△AGF(HL),∴∠BAF=∠GAF,
同理易得:△AGE≌△ADE,有∠GAE=∠DAE;
即∠EAF=∠EAG+∠FAG=12(∠DAG+∠BAG)
=12∠DAB=45°,
故∠EAF=45°.
?
归纳总结
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
正方形与平行四边形、矩形、菱形的关系
当堂检测
随堂练习
1.平行四边形、矩形、菱形、正方形都具有的性质是 ( )
A.对角线互相平分 B.对角线相互垂直
C.对角线相等 D.对角线互相垂直平分且相等
2.如图,在菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的周长为 ( )
A.14 B.15 C.12 D.17
A
C
A
B
C
D
E
F
60°
当堂检测
45°
正方形
12cm
2a+1
3.正方形的一边和对角线的夹角为___________.
4.如果一个四边形既是菱形又是矩形,那么它一定是_________.
5.已知正方形的面积为9cm?,它的周长为 _______________.
6.正方形的边长为a,当边长增加1时,其面积增加了__________.
O
A
B
C
D
7. 已知正方形ABCD在直角坐标系内,点A的坐标为(0,1),
点B的坐标为(0,0),则点C,D的坐标分别为________
和________.(只写一组)
8. 如图,在正方形ABCD中,E是对角线AC上一点,
且AE=AB,则∠EBC的度数是 .
A
D
B
C
O
E
(1,0)
(1,1)
22.5°
当堂检测
11.正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
9.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
30°
16cm
10.以正方形ABCD的边DC向外作等边△DCE,则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
M
A
B
C
D
E
F
O
当堂检测
12.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,
面积为AD2=8.
当堂检测
13.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC , PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
