第十八章 平行四边形复盘提升 单元复习课件(共30张PPT)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 第十八章 平行四边形复盘提升 单元复习课件(共30张PPT)-八年级数学下册同步精品课堂(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 25.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 20:41:01 | ||
图片预览






文档简介
(共30张PPT)
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
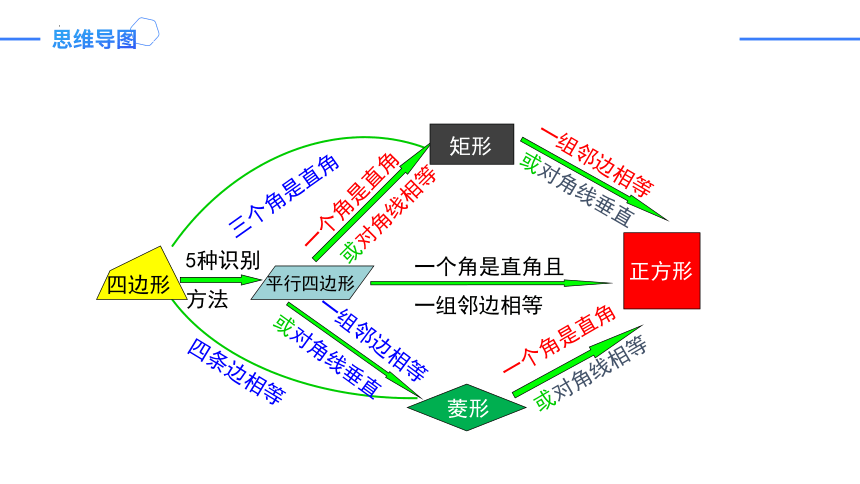
思维导图
5种识别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
探究思维
思考:把一块矩形纸板放在阳光下,它的影子可能是哪些图形?
研究内容
研究步骤
研究方法
平行四
边形
矩形
菱形
正方形
边、角、对
角线的特征
下定义→探性 质→研判定
观察、猜想、证明;把四边形问
题转化为三角形问题;从性质定
理的逆命题讨论中研究判定定理
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比平行四边形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,类
比平行四边形和矩形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比矩形和菱形
知识串讲
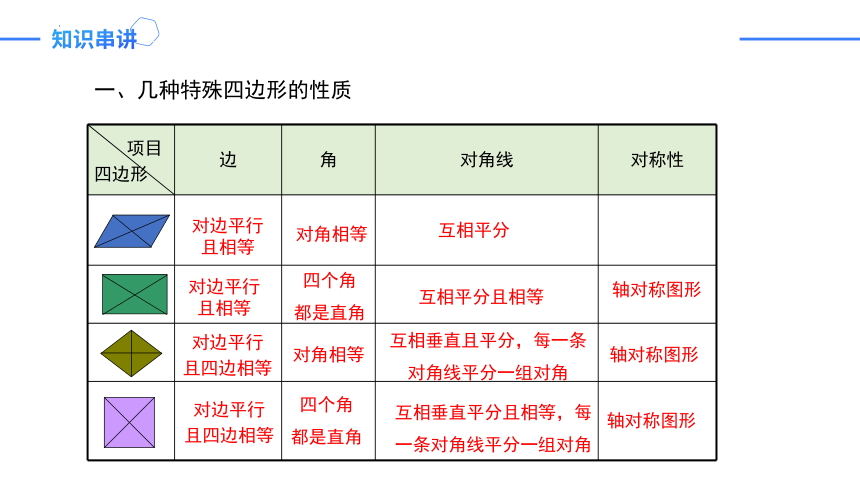
一、几种特殊四边形的性质
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
知识串讲
四边形 条件
平行 四边形
矩形
菱形
正方形
二、几种特殊四边形的常用判定方法:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形,3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
知识串讲
四、其他重要概念及性质
1.两条平行线之间的距离:
2.三角形的中位线定理:
两条平行线中,一条直线上任意一点到另一条直线的距离叫做两条平行线之间的距离.
三角形的中位线平行于第三边,并且等于第三边的一半.
3.直角三角形斜边上的中线:
直角三角形斜边上的中线等于斜边的一半.
考点梳理
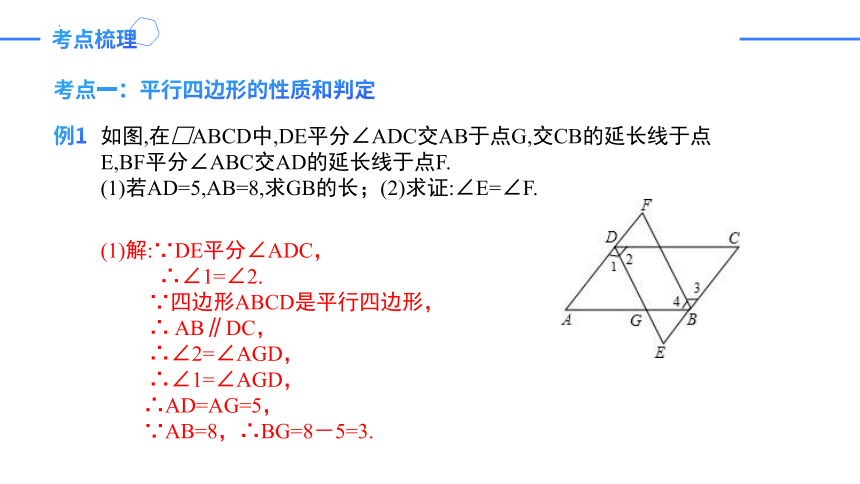
例1
如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的延长线于点E,BF平分∠ABC交AD的延长线于点F.
(1)若AD=5,AB=8,求GB的长;(2)求证:∠E=∠F.
(1)解:∵DE平分∠ADC,
∴∠1=∠2.
∵四边形ABCD是平行四边形,
∴ AB∥DC,
∴∠2=∠AGD,
∴∠1=∠AGD,
∴AD=AG=5,
∵AB=8,∴BG=8-5=3.
考点一:平行四边形的性质和判定
考点梳理
例1
(2)证明:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,DC∥AB,AD∥BC.
∵ DE平分∠ADC, BF平分∠ABC,
∴ ∠2= ∠4.
∵ DC∥AB,
∴ ∠2=∠AGD,
∴ ∠4=∠AGD,
∴ DE∥FB.
∵AF∥CE,
∴ 四边形BFDE是平行四边形,
∴ ∠E=∠F.
如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的延长线于点E,BF平分∠ABC交AD的延长线于点F.
(1)若AD=5,AB=8,求GB的长;(2)求证:∠E=∠F.
刻意练习
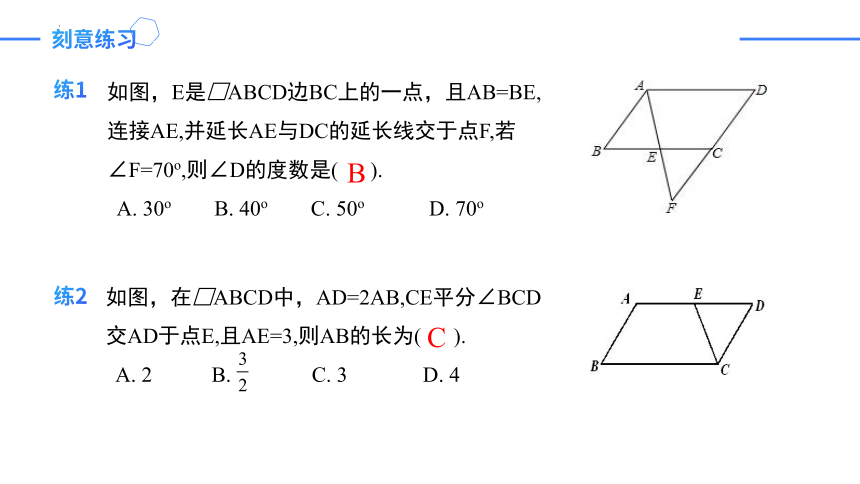
练1
如图,E是□ABCD边BC上的一点,且AB=BE,连接AE,并延长AE与DC的延长线交于点F,若∠F=70o,则∠D的度数是( ).
A. 30o B. 40o C. 50o D. 70o
B
如图,在□ABCD中,AD=2AB,CE平分∠BCD
交AD于点E,且AE=3,则AB的长为( ).
A. 2 B. C. 3 D. 4
C
练2
刻意练习
练3
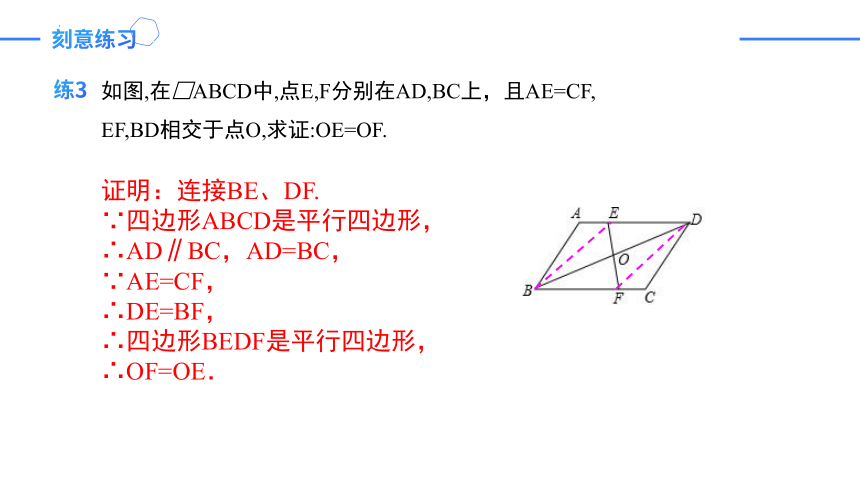
如图,在□ABCD中,点E,F分别在AD,BC上,且AE=CF,
EF,BD相交于点O,求证:OE=OF.
证明:连接BE、DF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OF=OE.
考点梳理
考点二:三角形的中位线
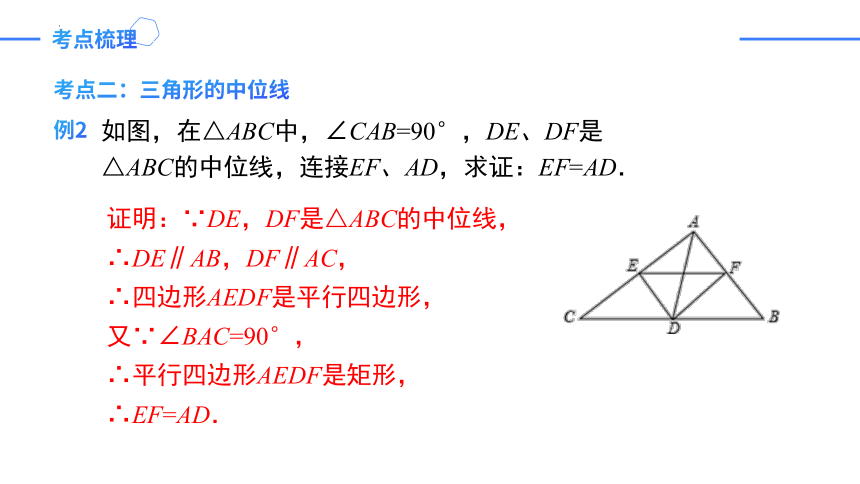
例2
如图,在△ABC中,∠CAB=90°,DE、DF是△ABC的中位线,连接EF、AD,求证:EF=AD.
证明:∵DE,DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,
∴平行四边形AEDF是矩形,
∴EF=AD.
考点梳理
例3
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF= BC.
若AB=12,求EF的长.
解:连接CD,
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,DE= BC,DC= AB.
∵CF= BC,
∴DE ∥FC,DE =FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∴EF= AB=6.
刻意练习
练4
如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
A.8 B.10 C.12 D.16
D
如图,在 ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于 ( )
A.2 B.3 C.4 D.5
C
练5
刻意练习
练6
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
证明:(1)∵点D,E,F分别是
AB,BC,CA的中点,
∴DE、EF都是△ABC的中位线,
∴EF∥AB,DE∥AC,
∴四边形ADEF是平行四边形.
刻意练习
练6
(2)∵四边形ADEF是平行四边形,
∴∠DEF=∠BAC,
∵D,F分别是AB,CA的中点,
AH是边BC上的高,
∴DH=AD,FH=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∵∠DAH+∠FAH=∠BAC,
∠DHA+∠FHA=∠DHF,
∴∠DHF=∠BAC,
∴∠DHF=∠DEF.
考点梳理
考点三:特殊平行四边形的性质与判定
例4
如图,在□ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形, AB=4,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴OA= OC,OB = OD.
又∵△ABO是等边三角形,
∴OA= OB=AB= 4,∠BAC=60°.
∴AC= BD= 2OA = 2×4 = 8.
A
B
C
D
O
考点梳理
例4
∴□ABCD是矩形 (对角线相等的平行四边形是矩形).
∴∠ABC=90°(矩形的四个角都是直角) .
在Rt△ABC中,由勾股定理,得
AB2 + BC2 =AC2 ,
∴BC= .
∴S□ABCD=AB·BC=4× =
如图,在□ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形, AB=4,求□ABCD的面积.
A
B
C
D
O
考点梳理
例5
如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×6=3(菱形的对角线互相平分)
在等腰三角形ABC中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 6.
∴AC=
A
B
C
O
D
考点梳理
例6
如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.
理由如下:∵EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠3=∠1.
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,∴∠2=∠4,
考点梳理
例6
如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
∴EC=AE,∴BE=AE.
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形;
(2)当∠A=45°时,菱形BECF是正方形.
证明如下:∵∠A=45°,∠ACB=90°,
∴∠CBA=45°,∴∠EBF=2∠CBA=90°,
∴菱形BECF是正方形.
刻意练习
练7
证明:在△AOB中.
∵AB= , OA=2,OB=1.
∴AB2=AO2+OB2.
∴ △AOB是直角三角形, ∠AOB是直角.
∴AC⊥BD.
∴ □ABCD是菱形
(对角线垂直的平行四边形是菱形).
已知:如右图,在□ABCD中,对角线AC与BD相交于点O, AB= ,OA=2,OB=1. 求证: □ABCD是菱形.
A
B
C
O
D
刻意练习
练8
如图,O是菱形ABCD对角线的交点,作BE∥AC,CE∥BD,BE、CE交于点E,四边形CEBO是矩形吗?说出你的理由.
D
A
B
C
E
O
解:四边形CEBO是矩形.
理由如下:已知四边形ABCD是菱形.
∴AC⊥BD.
∴∠BOC=90°.
∵DE∥AC,CE∥BD,
∴四边形CEBO是平行四边形.
∴四边形CEBO是矩形(有一个角是直角的平行四边形是矩形).
刻意练习
练9
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
如图,过正方形ABCD的顶点B作直线 l,过A、C作l的垂线,
垂足分别为E,F.若AE=1,CF=3,则AB的长度为 .
A
B
C
D
E
F
l
A
O
D
C
B
F
E
4
练10
刻意练习
练11
如图,△ABC中,点O是AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角∠ACG的平分线于点F,连接AE、AF.
(1)求证:∠ECF=90°;
(2)当点O运动到何处时,四边形AECF是矩形?请说明理由;
(1)证明:∵CE平分∠BCO,
CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠ECF= ×180°=90°.
刻意练习
练11
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.理由如下:
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF.
又∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴OE=OF.
又∵当点O运动到AC的中点时,AO=CO,
∴四边形AECF是平行四边形.
∵∠ECF=90°,
∴四边形AECF是矩形.
(2)当点O运动到何处时,四边形AECF是矩形?请说明理由;
刻意练习
练11
解:当点O运动到AC的中点时,
且满足∠ACB为直角时,四边形AECF是正方形.
∵由(2)知当点O运动到AC的中点时,四边形AECF
是矩形,
已知MN∥BC,
当∠ACB=90°,
则∠AOF=∠COE=∠COF=∠AOE=90°,
即AC⊥EF,
∴四边形AECF是正方形.
(3)在(2)的条件下,△ABC应该满足什么条件时, 四边形AECF为正
方形.
考点梳理
练12
如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
(1)证明:∵四边形ABCD是正方形,
∴AB=AD.
在△ABE和△DAF中,
∴△ABE≌△DAF.
考点梳理
练12
(2) 解:∵四边形ABCD是正方形,
∴∠1+∠4=90°.
∵∠3=∠4,
∴∠1+∠3=90°,
∴∠AFD=90°.
在正方形ABCD中, AD∥BC,
∴∠1=∠AGB=30°.
在Rt△ADF中,∠AFD=90°,AD=2,
∴AF= ,DF=1.
由(1)得△ABE≌△DAF,
∴AE=DF=1,
∴EF=AF-AE= -1.
课程小结
平行四边形
四边形
正
方
形
矩形
菱形
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
思维导图
5种识别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
探究思维
思考:把一块矩形纸板放在阳光下,它的影子可能是哪些图形?
研究内容
研究步骤
研究方法
平行四
边形
矩形
菱形
正方形
边、角、对
角线的特征
下定义→探性 质→研判定
观察、猜想、证明;把四边形问
题转化为三角形问题;从性质定
理的逆命题讨论中研究判定定理
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比平行四边形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,类
比平行四边形和矩形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比矩形和菱形
知识串讲
一、几种特殊四边形的性质
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
知识串讲
四边形 条件
平行 四边形
矩形
菱形
正方形
二、几种特殊四边形的常用判定方法:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形,3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
知识串讲
四、其他重要概念及性质
1.两条平行线之间的距离:
2.三角形的中位线定理:
两条平行线中,一条直线上任意一点到另一条直线的距离叫做两条平行线之间的距离.
三角形的中位线平行于第三边,并且等于第三边的一半.
3.直角三角形斜边上的中线:
直角三角形斜边上的中线等于斜边的一半.
考点梳理
例1
如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的延长线于点E,BF平分∠ABC交AD的延长线于点F.
(1)若AD=5,AB=8,求GB的长;(2)求证:∠E=∠F.
(1)解:∵DE平分∠ADC,
∴∠1=∠2.
∵四边形ABCD是平行四边形,
∴ AB∥DC,
∴∠2=∠AGD,
∴∠1=∠AGD,
∴AD=AG=5,
∵AB=8,∴BG=8-5=3.
考点一:平行四边形的性质和判定
考点梳理
例1
(2)证明:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,DC∥AB,AD∥BC.
∵ DE平分∠ADC, BF平分∠ABC,
∴ ∠2= ∠4.
∵ DC∥AB,
∴ ∠2=∠AGD,
∴ ∠4=∠AGD,
∴ DE∥FB.
∵AF∥CE,
∴ 四边形BFDE是平行四边形,
∴ ∠E=∠F.
如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的延长线于点E,BF平分∠ABC交AD的延长线于点F.
(1)若AD=5,AB=8,求GB的长;(2)求证:∠E=∠F.
刻意练习
练1
如图,E是□ABCD边BC上的一点,且AB=BE,连接AE,并延长AE与DC的延长线交于点F,若∠F=70o,则∠D的度数是( ).
A. 30o B. 40o C. 50o D. 70o
B
如图,在□ABCD中,AD=2AB,CE平分∠BCD
交AD于点E,且AE=3,则AB的长为( ).
A. 2 B. C. 3 D. 4
C
练2
刻意练习
练3
如图,在□ABCD中,点E,F分别在AD,BC上,且AE=CF,
EF,BD相交于点O,求证:OE=OF.
证明:连接BE、DF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OF=OE.
考点梳理
考点二:三角形的中位线
例2
如图,在△ABC中,∠CAB=90°,DE、DF是△ABC的中位线,连接EF、AD,求证:EF=AD.
证明:∵DE,DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,
∴平行四边形AEDF是矩形,
∴EF=AD.
考点梳理
例3
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF= BC.
若AB=12,求EF的长.
解:连接CD,
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,DE= BC,DC= AB.
∵CF= BC,
∴DE ∥FC,DE =FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∴EF= AB=6.
刻意练习
练4
如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
A.8 B.10 C.12 D.16
D
如图,在 ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于 ( )
A.2 B.3 C.4 D.5
C
练5
刻意练习
练6
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
证明:(1)∵点D,E,F分别是
AB,BC,CA的中点,
∴DE、EF都是△ABC的中位线,
∴EF∥AB,DE∥AC,
∴四边形ADEF是平行四边形.
刻意练习
练6
(2)∵四边形ADEF是平行四边形,
∴∠DEF=∠BAC,
∵D,F分别是AB,CA的中点,
AH是边BC上的高,
∴DH=AD,FH=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∵∠DAH+∠FAH=∠BAC,
∠DHA+∠FHA=∠DHF,
∴∠DHF=∠BAC,
∴∠DHF=∠DEF.
考点梳理
考点三:特殊平行四边形的性质与判定
例4
如图,在□ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形, AB=4,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴OA= OC,OB = OD.
又∵△ABO是等边三角形,
∴OA= OB=AB= 4,∠BAC=60°.
∴AC= BD= 2OA = 2×4 = 8.
A
B
C
D
O
考点梳理
例4
∴□ABCD是矩形 (对角线相等的平行四边形是矩形).
∴∠ABC=90°(矩形的四个角都是直角) .
在Rt△ABC中,由勾股定理,得
AB2 + BC2 =AC2 ,
∴BC= .
∴S□ABCD=AB·BC=4× =
如图,在□ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形, AB=4,求□ABCD的面积.
A
B
C
D
O
考点梳理
例5
如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×6=3(菱形的对角线互相平分)
在等腰三角形ABC中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 6.
∴AC=
A
B
C
O
D
考点梳理
例6
如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.
理由如下:∵EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠3=∠1.
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,∴∠2=∠4,
考点梳理
例6
如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
∴EC=AE,∴BE=AE.
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形;
(2)当∠A=45°时,菱形BECF是正方形.
证明如下:∵∠A=45°,∠ACB=90°,
∴∠CBA=45°,∴∠EBF=2∠CBA=90°,
∴菱形BECF是正方形.
刻意练习
练7
证明:在△AOB中.
∵AB= , OA=2,OB=1.
∴AB2=AO2+OB2.
∴ △AOB是直角三角形, ∠AOB是直角.
∴AC⊥BD.
∴ □ABCD是菱形
(对角线垂直的平行四边形是菱形).
已知:如右图,在□ABCD中,对角线AC与BD相交于点O, AB= ,OA=2,OB=1. 求证: □ABCD是菱形.
A
B
C
O
D
刻意练习
练8
如图,O是菱形ABCD对角线的交点,作BE∥AC,CE∥BD,BE、CE交于点E,四边形CEBO是矩形吗?说出你的理由.
D
A
B
C
E
O
解:四边形CEBO是矩形.
理由如下:已知四边形ABCD是菱形.
∴AC⊥BD.
∴∠BOC=90°.
∵DE∥AC,CE∥BD,
∴四边形CEBO是平行四边形.
∴四边形CEBO是矩形(有一个角是直角的平行四边形是矩形).
刻意练习
练9
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
如图,过正方形ABCD的顶点B作直线 l,过A、C作l的垂线,
垂足分别为E,F.若AE=1,CF=3,则AB的长度为 .
A
B
C
D
E
F
l
A
O
D
C
B
F
E
4
练10
刻意练习
练11
如图,△ABC中,点O是AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角∠ACG的平分线于点F,连接AE、AF.
(1)求证:∠ECF=90°;
(2)当点O运动到何处时,四边形AECF是矩形?请说明理由;
(1)证明:∵CE平分∠BCO,
CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠ECF= ×180°=90°.
刻意练习
练11
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.理由如下:
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF.
又∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴OE=OF.
又∵当点O运动到AC的中点时,AO=CO,
∴四边形AECF是平行四边形.
∵∠ECF=90°,
∴四边形AECF是矩形.
(2)当点O运动到何处时,四边形AECF是矩形?请说明理由;
刻意练习
练11
解:当点O运动到AC的中点时,
且满足∠ACB为直角时,四边形AECF是正方形.
∵由(2)知当点O运动到AC的中点时,四边形AECF
是矩形,
已知MN∥BC,
当∠ACB=90°,
则∠AOF=∠COE=∠COF=∠AOE=90°,
即AC⊥EF,
∴四边形AECF是正方形.
(3)在(2)的条件下,△ABC应该满足什么条件时, 四边形AECF为正
方形.
考点梳理
练12
如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
(1)证明:∵四边形ABCD是正方形,
∴AB=AD.
在△ABE和△DAF中,
∴△ABE≌△DAF.
考点梳理
练12
(2) 解:∵四边形ABCD是正方形,
∴∠1+∠4=90°.
∵∠3=∠4,
∴∠1+∠3=90°,
∴∠AFD=90°.
在正方形ABCD中, AD∥BC,
∴∠1=∠AGB=30°.
在Rt△ADF中,∠AFD=90°,AD=2,
∴AF= ,DF=1.
由(1)得△ABE≌△DAF,
∴AE=DF=1,
∴EF=AF-AE= -1.
课程小结
平行四边形
四边形
正
方
形
矩形
菱形
