专题01 平面图形的认识(二)【考点串讲PPT】课件(共36张PPT)-七年级数学下学期期中考点大串讲(苏科版)
文档属性
| 名称 | 专题01 平面图形的认识(二)【考点串讲PPT】课件(共36张PPT)-七年级数学下学期期中考点大串讲(苏科版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 20:39:48 | ||
图片预览









文档简介
七年级苏科版数学下册期中考点大串讲
串讲01 平面图形的认识(二)
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
考点一 平行线的性质与判定
三线八角的概念:指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对. 正确认识这八个角要抓住:同位角位置相同即“同旁和同侧”;内错角要抓住“内部和异侧”;同旁内角要抓住“同旁和内部”.
平行线的定义:在同一平面内,不相交的两条直线叫做平行线,平行用符号“∥”表示.
平行公理(唯一性):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论(传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合.
平行线之间的距离概念:两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离.
性质:1)夹在两条平行线间的平行线段处处相等;
2)平行线间的距离处处相等.
知识大全
考点一 平行线的性质与判定
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补..
平行线的判定
判定方法1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行.
判定方法2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行.
判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行.
判定方法4:垂直于同一直线的两直线互相平行.
易错易混
考点一 平行线的性质与判定
1. 平行线必在同一平面内,分别在两个平面内的两条直线,即使不相交,也可以不平行,因此“在同一平面内”是平行线存在的前提条件.
2. 平行线指的是“两条直线”而不是两条射线或线段,今后遇到线段、射线平行时,特指线段、射线所在的直线平行.
3. 在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论. 这是平行线特有的性质不要一提同位角或内错角就认为它们相等,一提同旁内角就认为互补,若没有两直线平行的条件,这些是不成立的.
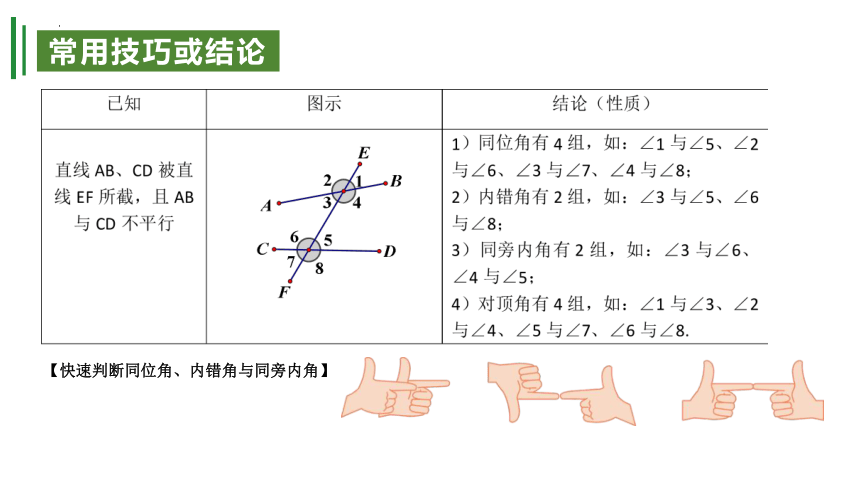
常用技巧或结论
【快速判断同位角、内错角与同旁内角】
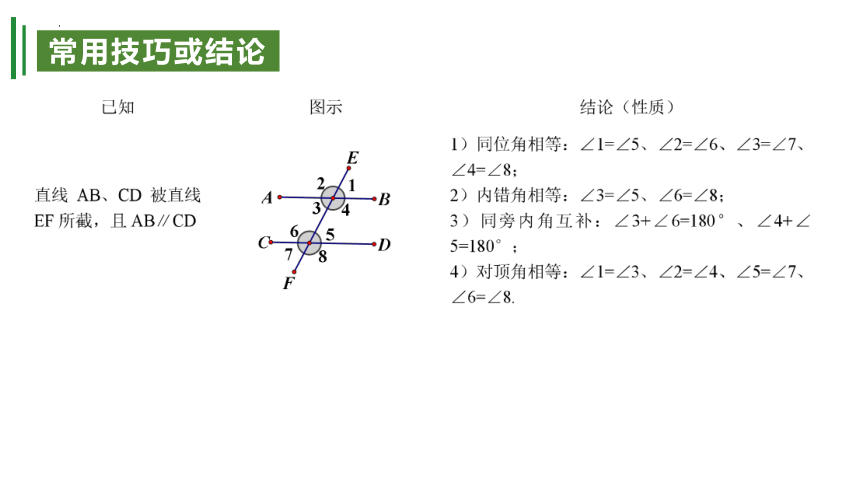
常用技巧或结论
热考题型
考点一 平行线的性质与判定
1(20-21七年级下·广东梅州·期中)如下图,在“????”字型图中,????????、????????被????????所截,则∠????与∠4是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
2(23-24七年级上·黑龙江哈尔滨·期中)如图,下列结论正确的是(????)
A.∠5与∠4是对顶角 B.∠1与∠3是同位角
C.∠2与∠3是同旁内角 D.∠1与∠2是同旁内角
?
热考题型
考点一 平行线的性质与判定
3(23-24七年级上·安徽宿州·期中)在同一平面内两条直线的位置关系可能是(????)
A.相交或垂直 B.垂直或平行 C.平行或相交 D.相交或重合
4(22-23七年级下·天津和平·期末)下列说法中正确的是(????)
A.过一点有且只有一条直线垂直于已知直线
B.直线外一点到这条直线的垂线段,叫做这点到这条直线距离
C.经过直线外一点,有且仅有一条直线与已知直线平行
D.两条直线被第三条直线所截,同旁内角互补
5(21-22七年级下·山东菏泽·期中)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(????)
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
热考题型
考点一 平行线的性质与判定
6(22-23七年级下·贵州贵阳·期末)如图,已知????????⊥????????,????????⊥????????,∠1=∠2,请判断????????与????????的位置关系,并说明理由.
?
【详解】解:????????与????????的位置关系是:????????∥????????,理由如下:
∵????????⊥????????,????????⊥????????,
∴∠????????????=90°,∠????????????=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∵∠1=∠2,
∴∠3=∠4,
∴????????∥????????.
?
热考题型
考点一 平行线的性质与判定
7(2022·浙江绍兴·中考真题)如图,把一块三角板????????????的直角顶点B放在直线????????上,∠????=30°,AC∥EF,则∠1=(????)
A.30° B.45°
C.60° D.75°
8(2022·陕西·中考真题)如图,????????∥????????,????????∥????????.若∠1=58°,则∠2的大小为(????)
A.120° B.122° C.132° D.148°
?
热考题型
考点一 平行线的性质与判定
9(21-22七年级下·湖南张家界·期末)如图:CD∥AB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是(????)
A.①②③ B.①②④ C.②③④ D.①②③④
?
10(21-22七年级下·湖北武汉·期中)如图,某人骑自行车自????沿正东方向前进,第一次在????处拐弯,两次拐弯后,仍沿正东方向行驶,两次拐弯的角度可能是( )
A.第一次右拐15°,第二次左拐165°
B.第一次右拐15°,第二次左拐15°
C.第一次左拐15°,第二次左拐165°
D.第一次右拐165°,第二次左拐165°
?
热考题型
考点一 平行线的性质与判定
11(21-22七年级下·重庆铜梁·期中)如图,已知????????∥????????,且∠C=110°,则∠1与∠2的数量关系为 .
?
【详解】解:过点C作????????∥????????,如图:
则????????∥????????∥????????,
∴∠????????????=∠1,∠????????????+∠2=180°,
∵∠????????????=110°,
∴∠????????????=110°?∠????????????=110°?∠1,
∴110°?∠1+∠2=180°,
∴∠2=∠1+70°.
【解题方法】遇“拐点”,作平行线
?
知识大全
考点二 三角形的概念及性质
三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所构成的图形叫做三角形.
三角形的表示:用符号“Δ”表示,顶点是A、B、C的三角形记作“ΔABC”,读作“三角形ABC”.
三角形的分类:
1)三角形按边分类:三角形三边都不相等的三角形???????????????????????????????????????等腰三角形等边三角形???????????????????????????????????底边和腰不相等的等腰三角形
2)三角形按角分类:三角形直角三角形??????????????????斜三角形锐角三角形钝角三角形
?
三角形的稳定性: 三角形三条边的长度确定之后,三角形的形状就唯一确定了.
?
知识大全
考点二 三角形的概念及性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}重要线段
概念
图形
性质
三角形的高
从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高).
∵AD是?ABC中BC边的高
∴∠ADB=∠ADC=90°
三角形的中线
在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线
∵AD是?ABC中BC边的中线
∴BD=CD S△ABD=S△ADC
三角形的角平分线
三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线.
∵AD是?ABC中∠BAC的角平分线
∴∠BAD=∠DAC=∠BAC
知识大全
考点二 三角形的概念及性质
三角形三边关系定理:三角形的两边之和大于第三边.
推论:三角形的两边之差小于第三边.
三角形的内角和定理:三角形三个内角和等于180°.
推论:直角三角形的两个锐角互余.
三角形的内角和定理的应用:
1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数;
2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数;
3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数.
三角形的外角和定理:三角形的外角和等于360°.
三角形的外角和的性质:1)三角形的一个外角等于和它不相邻的两个内角的和;
2)三角形的一个外角大于任何一个和它不相邻的内角.
常用技巧或结论
三角形的稳定性解题技巧:
1)当三角形三条边的长度确定之后,三角形的形状就唯一确定了.
2)四边形及多边形不具有稳定性,要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了.
三角形三边关系定理及推论的应用:
1)判断三条已知线段能否组成三角形,只需检验最短的两边之和大于第三边,则可说明能组成三角形.
2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b
3)所有通过周长相加减求三角形的边,求出两个答案的,要注意检查每个答案能否组成三角形.
热考题型
考点二 三角形的概念及性质
1.(23-24七年级上·山东烟台·期中)如图所示的五边形边框,木匠师傅至少需要再钉 根木条才能使其不变形.
2.(22-23七年级下·山东枣庄·期末)如图,????????,????????,????????分别是△????????????的中线、角平分线、高线,下列结论中错误的是(????)
A.????????=12???????? B.2∠????????????=∠????????????
C.∠????+∠????????????=90° D.????????=????????
?
热考题型
考点二 三角形的概念及性质
3.(23-24七年级上·江苏盐城·期末)如图,在△????????????中,∠????<∠????,????????为????????边的中线,△????????????的周长比△????????????的周长大3,????????=8,则????????= .
?
【详解】解:∵????????为????????边的中线,∴????????=????????,
∵△????????????的周长比△????????????的周长大3,
∴????????+????????+?????????????????+????????+????????=3,∴?????????????????=3,
∵????????=8,∴????????=5,
?
热考题型
考点二 三角形的概念及性质
4.(22-23七年级下·黑龙江哈尔滨·期中)如图是10×8的网格,网格中每个小正方形的边长均为1,△????????????的三个顶点A、B、C都在小正方形的顶点上,请在图中分别按要求画图:
(1)在图中画△????????????的中线????????;
(2)在图中画△????????????的高线????????.
(3)直接写出△????????????的面积是________.
?
(3)解:????△????????????=12×8×2=8,
?
热考题型
考点二 三角形的概念及性质
5.(21-22七年级下·江苏南京·期末)已知三角形三边长分别为2,9,????,若????为偶数,则这样的三角形有 个.
?
【详解】解:∵三角形三边长分别为2,9,????∴7∵x为偶数,∴x可能是8和10,即这样的三角形有2个.
?
6.【易错必考】(23-24八年级上·湖北武汉·期中)已知等腰三角形的一边长为4,一边长为9,则它的周长为 .
【详解】解:当腰长为4,底边长为9时,4+4=8<9,不能组成三角形,不符合题意;
当腰长为9,底边长为4时,4+9=13>9,能组成三角形,符合题意,此时周长为4+9+9=22,
?
热考题型
考点二 三角形的概念及性质
热考题型
考点二 三角形的概念及性质
8.(22-23七年级上·山东威海·期末)如图,将△????????????沿着????????对折,点A落到????′处,若∠????????????′+∠????????????′=82°,则∠????= ??度.
?
【详解】解:∵将△????????????沿着????????对折,A落到????′,
∴∠????????????=∠????′????????,∠????????????=∠????′????????,
∴∠????????????′+2∠????????????=180°,∠????′????????+2∠????????????=180°,
∴∠????????????′+2∠????????????+∠????′????????+2∠????????????=360°,
∵∠????????????′+∠????????????′=82°,
∴∠????????????+∠????????????=139°,
∴∠????=180°?∠????????????+∠????????????=180°?139°=41°,
?
9.(22-23七年级下·四川成都·期末)若直角三角形的一个锐角等于40°,则它的另一个锐角等于(????)
A.50° B.60° C.70° D.140°
?
热考题型
考点二 三角形的概念及性质
10.(20-21七年级下·云南西双版纳·期中)如图,????1∥????2,点O在直线????1上,且∠????????????=90°,若∠2=51°,则∠1= .
?
【详解】解:∵∠2=51°, ∴∠????????????=∠2=51°,
∵∠????????????=90°,∴∠????????????=90°?51°=39°,
∵????1∥????2,∴∠????????????=∠1=39°,
?
11.(23-24八年级上·重庆城口·期末)抖空竹是我国独有的民族体育运动之一,作为一种中国古老的技艺,有着悠久的历史和传统,2006年,抖空竹被列入国家级非物质文化遗产代表性项目名录.如图1,小亮同学用数学抽象思维绘制出如图2,已知????????∥????????,∠????=21°,∠????=37°,则∠????的度数是 .
?
【详解】解:∵ ????????∥????????,
∴∠????????????=∠????=37°,
∵∠????=21°,
∴∠????=∠?????????????∠????=16°.
?
知识大全
考点三 图形的平移
平移的概念:在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.平移不改变图形的形状和大小.
平移的三大要素:1)平移的起点,2)平移的方向,3)平移的距离.
作图步骤:
1)根据题意,确定平移的方向和平移的距离;
2)找出原图形的关键点;
3)按平移方向和平移距离平移各个关键点,得到各关键点的对应点;
4)按原图形依次连接对应点,得到平移后的图形.
平移的性质:
1)平移不改变图形的大小、形状,只改变图形的位置,因此平移前后的两个图形全等.
2)平移前后对应线段平行且相等、对应角相等.
3)任意两组对应点的连线平行(或在同一条直线上)且相等,对应点之间的距离就是平移的距离.
热考题型
考点三 图形的平移
1.(22-23七年级下·四川广元·期中)下面生活中的现象可以看成平移的是(????)
①转动的指针②水平传输带上物品的运动③从楼顶自由下落的铁球(球不旋转)④随风摆动的旗帜
A.①② B.③④ C.②③ D.②④
热考题型
考点三 图形的平移
3.(22-23七年级下·吉林长春·期末)如图,△????????????的周长为12cm,若将△????????????沿射线????????方向平移3cm后得到△????????????,????????与????????相交点????,连结????????,则△????????????与△????????????的周长和为(????)
A.15cm B.13cm C.12cm D.9cm
?
【详解】解:由平移的性质可得,????????=????????,????????=????????,
∴△????????????与△????????????的周长和=????????+????????+????????+????????+????????+????????,
=????????+????????+????????+????????+????????+????????,
=????????+????????+????????,
=????????+????????+????????,
∵△????????????的周长为12cm,
∴????????+????????+????????=12cm,
∴△????????????与△????????????的周长和为12cm,
故选:C.
?
热考题型
考点三 图形的平移
4.(22-23七年级下·黑龙江鸡西·期中)春天到了,为美化环境,鸡西市儿童公园在一块长方形的空地上修两条宽一米的小路,其余部分种上不同的花卉,测得数据如图所示,求种花的面积和为 .
【详解】解:根据题意可知,种花的面积和为:
5?1×3?1=4×2=8.
故答案为:8.
?
知识大全
考点四 多边形的内角和与外角和
多边形的定义:在平面中,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
多边形的对角线:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.?
多边形内角和定理:n边形的内角和为(n?2)?180°(n≥3).
多边形外角和定理:任意多边形的外角和等于360°,与多边形的形状和边数无关.
正多边形的定义:各角相等,各边相等的多边形叫做正多边形.
解题技巧
考点四 多边形的内角和与外角和
1)正n边形的每个内角为(n?2)×180°????,每一个外角为360°????.
2)正n边形有n条对称轴.
3)对于正n边形,当n为奇数时,是轴对称图形;当n为偶数时,既是轴对称图形,又是中心对称图形.
4)从n边形的一个顶点可以引(n-3)条对角线,并且这些对角线把多边形分成了(n–2)个三角形,n边形的对角线条数为????(?????3)2?
?
解题技巧
考点四 多边形的内角和与外角和
1)n边形的内角和随边数的增加而增加,边数每增加1,内角和增加180°.
2)任意多边形的内角和均为180°的整数倍.
3)利用多边形内角和定理可解决三类问题:
①已知多边形的边数求内角和;
②已知多边形的内角和求边数;
③已知足够的角度条件下求某一个内角的度数.
热考题型
考点四 多边形的内角和与外角和
1.(23-24七年级上·贵州毕节·期末)若从多边形的一个顶点出发,最多可引3条对角线,则这个多边形的对角线共有(????)
A.6条 B.9条 C.12条 D.18条
2.(23-24九年级上·四川绵阳·期末)从十二边形的一个顶点引对角线,可把这个多边形分成(????)个三角形.
A.10 B.11 C.12 D.13
3.(22-23七年级下·广东惠州·开学考试)一个多边形的内角和是720°,则这个多边形的边数是
?
6
?
4(22-23七年级下·甘肃天水·期末)如图,小明在操场上从????点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地????点时,一共走了(????)米
A.56 B.64 C.80 D.72
?
热考题型
考点四 多边形的内角和与外角和
5.(22-23七年级上·湖北武汉·阶段练习)一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是( )
A.9 B.10 C.8或9或10 D.9或10或11
【详解】解:设内角和为1440°的多边形的边数是n,则(n-2)?180=1440,解得:n=10.
∵截去一个角后边上可以增加1,不变,减少1,∴原多边形的边数是9或10或11.故选:D.
【解题技巧】一个n变形剪去一个角后,若剪去的一个角只经过一个顶点和一边,则剩下的形状是n边形,若剪去的一个角经过两条邻边,则剩下的形状是(n+1)边形,若剪去的一个角经过两个相邻点,则剩下的形状是(n-1)边形.所以遇到相关题目时,要分类讨论.
热考题型
考点四 多边形的内角和与外角和
6.(22-23七年级下·福建泉州·期末)正四边形与其他正多边形组合可以铺设地板,则该多边形可以是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【详解】解:A.正五边形每个内角108°,正四边形每个内角90°,显然不能组合成360°,所以不能铺设地板,不符合题意;
B.正六边形每个内角120°,正四边形每个内角90°,不能组合成360°,所以不能铺设地板,不符合题意;
C.正四边形每个内角90°,正八边形每个内角135°,90°+135°×2=360°,所以能铺设地板,符合题意;
D.因为十边形的每个内角是144°,正四边形的每个内角是90°,不能组合成360°,所以不能铺设地板,不符合题意;故选:C.
?
【解题技巧】解决几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
谢谢!
串讲01 平面图形的认识(二)
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
考点一 平行线的性质与判定
三线八角的概念:指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对. 正确认识这八个角要抓住:同位角位置相同即“同旁和同侧”;内错角要抓住“内部和异侧”;同旁内角要抓住“同旁和内部”.
平行线的定义:在同一平面内,不相交的两条直线叫做平行线,平行用符号“∥”表示.
平行公理(唯一性):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论(传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合.
平行线之间的距离概念:两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离.
性质:1)夹在两条平行线间的平行线段处处相等;
2)平行线间的距离处处相等.
知识大全
考点一 平行线的性质与判定
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补..
平行线的判定
判定方法1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行.
判定方法2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行.
判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行.
判定方法4:垂直于同一直线的两直线互相平行.
易错易混
考点一 平行线的性质与判定
1. 平行线必在同一平面内,分别在两个平面内的两条直线,即使不相交,也可以不平行,因此“在同一平面内”是平行线存在的前提条件.
2. 平行线指的是“两条直线”而不是两条射线或线段,今后遇到线段、射线平行时,特指线段、射线所在的直线平行.
3. 在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论. 这是平行线特有的性质不要一提同位角或内错角就认为它们相等,一提同旁内角就认为互补,若没有两直线平行的条件,这些是不成立的.
常用技巧或结论
【快速判断同位角、内错角与同旁内角】
常用技巧或结论
热考题型
考点一 平行线的性质与判定
1(20-21七年级下·广东梅州·期中)如下图,在“????”字型图中,????????、????????被????????所截,则∠????与∠4是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
2(23-24七年级上·黑龙江哈尔滨·期中)如图,下列结论正确的是(????)
A.∠5与∠4是对顶角 B.∠1与∠3是同位角
C.∠2与∠3是同旁内角 D.∠1与∠2是同旁内角
?
热考题型
考点一 平行线的性质与判定
3(23-24七年级上·安徽宿州·期中)在同一平面内两条直线的位置关系可能是(????)
A.相交或垂直 B.垂直或平行 C.平行或相交 D.相交或重合
4(22-23七年级下·天津和平·期末)下列说法中正确的是(????)
A.过一点有且只有一条直线垂直于已知直线
B.直线外一点到这条直线的垂线段,叫做这点到这条直线距离
C.经过直线外一点,有且仅有一条直线与已知直线平行
D.两条直线被第三条直线所截,同旁内角互补
5(21-22七年级下·山东菏泽·期中)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(????)
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
热考题型
考点一 平行线的性质与判定
6(22-23七年级下·贵州贵阳·期末)如图,已知????????⊥????????,????????⊥????????,∠1=∠2,请判断????????与????????的位置关系,并说明理由.
?
【详解】解:????????与????????的位置关系是:????????∥????????,理由如下:
∵????????⊥????????,????????⊥????????,
∴∠????????????=90°,∠????????????=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∵∠1=∠2,
∴∠3=∠4,
∴????????∥????????.
?
热考题型
考点一 平行线的性质与判定
7(2022·浙江绍兴·中考真题)如图,把一块三角板????????????的直角顶点B放在直线????????上,∠????=30°,AC∥EF,则∠1=(????)
A.30° B.45°
C.60° D.75°
8(2022·陕西·中考真题)如图,????????∥????????,????????∥????????.若∠1=58°,则∠2的大小为(????)
A.120° B.122° C.132° D.148°
?
热考题型
考点一 平行线的性质与判定
9(21-22七年级下·湖南张家界·期末)如图:CD∥AB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是(????)
A.①②③ B.①②④ C.②③④ D.①②③④
?
10(21-22七年级下·湖北武汉·期中)如图,某人骑自行车自????沿正东方向前进,第一次在????处拐弯,两次拐弯后,仍沿正东方向行驶,两次拐弯的角度可能是( )
A.第一次右拐15°,第二次左拐165°
B.第一次右拐15°,第二次左拐15°
C.第一次左拐15°,第二次左拐165°
D.第一次右拐165°,第二次左拐165°
?
热考题型
考点一 平行线的性质与判定
11(21-22七年级下·重庆铜梁·期中)如图,已知????????∥????????,且∠C=110°,则∠1与∠2的数量关系为 .
?
【详解】解:过点C作????????∥????????,如图:
则????????∥????????∥????????,
∴∠????????????=∠1,∠????????????+∠2=180°,
∵∠????????????=110°,
∴∠????????????=110°?∠????????????=110°?∠1,
∴110°?∠1+∠2=180°,
∴∠2=∠1+70°.
【解题方法】遇“拐点”,作平行线
?
知识大全
考点二 三角形的概念及性质
三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所构成的图形叫做三角形.
三角形的表示:用符号“Δ”表示,顶点是A、B、C的三角形记作“ΔABC”,读作“三角形ABC”.
三角形的分类:
1)三角形按边分类:三角形三边都不相等的三角形???????????????????????????????????????等腰三角形等边三角形???????????????????????????????????底边和腰不相等的等腰三角形
2)三角形按角分类:三角形直角三角形??????????????????斜三角形锐角三角形钝角三角形
?
三角形的稳定性: 三角形三条边的长度确定之后,三角形的形状就唯一确定了.
?
知识大全
考点二 三角形的概念及性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}重要线段
概念
图形
性质
三角形的高
从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高).
∵AD是?ABC中BC边的高
∴∠ADB=∠ADC=90°
三角形的中线
在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线
∵AD是?ABC中BC边的中线
∴BD=CD S△ABD=S△ADC
三角形的角平分线
三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线.
∵AD是?ABC中∠BAC的角平分线
∴∠BAD=∠DAC=∠BAC
知识大全
考点二 三角形的概念及性质
三角形三边关系定理:三角形的两边之和大于第三边.
推论:三角形的两边之差小于第三边.
三角形的内角和定理:三角形三个内角和等于180°.
推论:直角三角形的两个锐角互余.
三角形的内角和定理的应用:
1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数;
2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数;
3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数.
三角形的外角和定理:三角形的外角和等于360°.
三角形的外角和的性质:1)三角形的一个外角等于和它不相邻的两个内角的和;
2)三角形的一个外角大于任何一个和它不相邻的内角.
常用技巧或结论
三角形的稳定性解题技巧:
1)当三角形三条边的长度确定之后,三角形的形状就唯一确定了.
2)四边形及多边形不具有稳定性,要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了.
三角形三边关系定理及推论的应用:
1)判断三条已知线段能否组成三角形,只需检验最短的两边之和大于第三边,则可说明能组成三角形.
2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b
3)所有通过周长相加减求三角形的边,求出两个答案的,要注意检查每个答案能否组成三角形.
热考题型
考点二 三角形的概念及性质
1.(23-24七年级上·山东烟台·期中)如图所示的五边形边框,木匠师傅至少需要再钉 根木条才能使其不变形.
2.(22-23七年级下·山东枣庄·期末)如图,????????,????????,????????分别是△????????????的中线、角平分线、高线,下列结论中错误的是(????)
A.????????=12???????? B.2∠????????????=∠????????????
C.∠????+∠????????????=90° D.????????=????????
?
热考题型
考点二 三角形的概念及性质
3.(23-24七年级上·江苏盐城·期末)如图,在△????????????中,∠????<∠????,????????为????????边的中线,△????????????的周长比△????????????的周长大3,????????=8,则????????= .
?
【详解】解:∵????????为????????边的中线,∴????????=????????,
∵△????????????的周长比△????????????的周长大3,
∴????????+????????+?????????????????+????????+????????=3,∴?????????????????=3,
∵????????=8,∴????????=5,
?
热考题型
考点二 三角形的概念及性质
4.(22-23七年级下·黑龙江哈尔滨·期中)如图是10×8的网格,网格中每个小正方形的边长均为1,△????????????的三个顶点A、B、C都在小正方形的顶点上,请在图中分别按要求画图:
(1)在图中画△????????????的中线????????;
(2)在图中画△????????????的高线????????.
(3)直接写出△????????????的面积是________.
?
(3)解:????△????????????=12×8×2=8,
?
热考题型
考点二 三角形的概念及性质
5.(21-22七年级下·江苏南京·期末)已知三角形三边长分别为2,9,????,若????为偶数,则这样的三角形有 个.
?
【详解】解:∵三角形三边长分别为2,9,????∴7∵x为偶数,∴x可能是8和10,即这样的三角形有2个.
?
6.【易错必考】(23-24八年级上·湖北武汉·期中)已知等腰三角形的一边长为4,一边长为9,则它的周长为 .
【详解】解:当腰长为4,底边长为9时,4+4=8<9,不能组成三角形,不符合题意;
当腰长为9,底边长为4时,4+9=13>9,能组成三角形,符合题意,此时周长为4+9+9=22,
?
热考题型
考点二 三角形的概念及性质
热考题型
考点二 三角形的概念及性质
8.(22-23七年级上·山东威海·期末)如图,将△????????????沿着????????对折,点A落到????′处,若∠????????????′+∠????????????′=82°,则∠????= ??度.
?
【详解】解:∵将△????????????沿着????????对折,A落到????′,
∴∠????????????=∠????′????????,∠????????????=∠????′????????,
∴∠????????????′+2∠????????????=180°,∠????′????????+2∠????????????=180°,
∴∠????????????′+2∠????????????+∠????′????????+2∠????????????=360°,
∵∠????????????′+∠????????????′=82°,
∴∠????????????+∠????????????=139°,
∴∠????=180°?∠????????????+∠????????????=180°?139°=41°,
?
9.(22-23七年级下·四川成都·期末)若直角三角形的一个锐角等于40°,则它的另一个锐角等于(????)
A.50° B.60° C.70° D.140°
?
热考题型
考点二 三角形的概念及性质
10.(20-21七年级下·云南西双版纳·期中)如图,????1∥????2,点O在直线????1上,且∠????????????=90°,若∠2=51°,则∠1= .
?
【详解】解:∵∠2=51°, ∴∠????????????=∠2=51°,
∵∠????????????=90°,∴∠????????????=90°?51°=39°,
∵????1∥????2,∴∠????????????=∠1=39°,
?
11.(23-24八年级上·重庆城口·期末)抖空竹是我国独有的民族体育运动之一,作为一种中国古老的技艺,有着悠久的历史和传统,2006年,抖空竹被列入国家级非物质文化遗产代表性项目名录.如图1,小亮同学用数学抽象思维绘制出如图2,已知????????∥????????,∠????=21°,∠????=37°,则∠????的度数是 .
?
【详解】解:∵ ????????∥????????,
∴∠????????????=∠????=37°,
∵∠????=21°,
∴∠????=∠?????????????∠????=16°.
?
知识大全
考点三 图形的平移
平移的概念:在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.平移不改变图形的形状和大小.
平移的三大要素:1)平移的起点,2)平移的方向,3)平移的距离.
作图步骤:
1)根据题意,确定平移的方向和平移的距离;
2)找出原图形的关键点;
3)按平移方向和平移距离平移各个关键点,得到各关键点的对应点;
4)按原图形依次连接对应点,得到平移后的图形.
平移的性质:
1)平移不改变图形的大小、形状,只改变图形的位置,因此平移前后的两个图形全等.
2)平移前后对应线段平行且相等、对应角相等.
3)任意两组对应点的连线平行(或在同一条直线上)且相等,对应点之间的距离就是平移的距离.
热考题型
考点三 图形的平移
1.(22-23七年级下·四川广元·期中)下面生活中的现象可以看成平移的是(????)
①转动的指针②水平传输带上物品的运动③从楼顶自由下落的铁球(球不旋转)④随风摆动的旗帜
A.①② B.③④ C.②③ D.②④
热考题型
考点三 图形的平移
3.(22-23七年级下·吉林长春·期末)如图,△????????????的周长为12cm,若将△????????????沿射线????????方向平移3cm后得到△????????????,????????与????????相交点????,连结????????,则△????????????与△????????????的周长和为(????)
A.15cm B.13cm C.12cm D.9cm
?
【详解】解:由平移的性质可得,????????=????????,????????=????????,
∴△????????????与△????????????的周长和=????????+????????+????????+????????+????????+????????,
=????????+????????+????????+????????+????????+????????,
=????????+????????+????????,
=????????+????????+????????,
∵△????????????的周长为12cm,
∴????????+????????+????????=12cm,
∴△????????????与△????????????的周长和为12cm,
故选:C.
?
热考题型
考点三 图形的平移
4.(22-23七年级下·黑龙江鸡西·期中)春天到了,为美化环境,鸡西市儿童公园在一块长方形的空地上修两条宽一米的小路,其余部分种上不同的花卉,测得数据如图所示,求种花的面积和为 .
【详解】解:根据题意可知,种花的面积和为:
5?1×3?1=4×2=8.
故答案为:8.
?
知识大全
考点四 多边形的内角和与外角和
多边形的定义:在平面中,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
多边形的对角线:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.?
多边形内角和定理:n边形的内角和为(n?2)?180°(n≥3).
多边形外角和定理:任意多边形的外角和等于360°,与多边形的形状和边数无关.
正多边形的定义:各角相等,各边相等的多边形叫做正多边形.
解题技巧
考点四 多边形的内角和与外角和
1)正n边形的每个内角为(n?2)×180°????,每一个外角为360°????.
2)正n边形有n条对称轴.
3)对于正n边形,当n为奇数时,是轴对称图形;当n为偶数时,既是轴对称图形,又是中心对称图形.
4)从n边形的一个顶点可以引(n-3)条对角线,并且这些对角线把多边形分成了(n–2)个三角形,n边形的对角线条数为????(?????3)2?
?
解题技巧
考点四 多边形的内角和与外角和
1)n边形的内角和随边数的增加而增加,边数每增加1,内角和增加180°.
2)任意多边形的内角和均为180°的整数倍.
3)利用多边形内角和定理可解决三类问题:
①已知多边形的边数求内角和;
②已知多边形的内角和求边数;
③已知足够的角度条件下求某一个内角的度数.
热考题型
考点四 多边形的内角和与外角和
1.(23-24七年级上·贵州毕节·期末)若从多边形的一个顶点出发,最多可引3条对角线,则这个多边形的对角线共有(????)
A.6条 B.9条 C.12条 D.18条
2.(23-24九年级上·四川绵阳·期末)从十二边形的一个顶点引对角线,可把这个多边形分成(????)个三角形.
A.10 B.11 C.12 D.13
3.(22-23七年级下·广东惠州·开学考试)一个多边形的内角和是720°,则这个多边形的边数是
?
6
?
4(22-23七年级下·甘肃天水·期末)如图,小明在操场上从????点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地????点时,一共走了(????)米
A.56 B.64 C.80 D.72
?
热考题型
考点四 多边形的内角和与外角和
5.(22-23七年级上·湖北武汉·阶段练习)一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是( )
A.9 B.10 C.8或9或10 D.9或10或11
【详解】解:设内角和为1440°的多边形的边数是n,则(n-2)?180=1440,解得:n=10.
∵截去一个角后边上可以增加1,不变,减少1,∴原多边形的边数是9或10或11.故选:D.
【解题技巧】一个n变形剪去一个角后,若剪去的一个角只经过一个顶点和一边,则剩下的形状是n边形,若剪去的一个角经过两条邻边,则剩下的形状是(n+1)边形,若剪去的一个角经过两个相邻点,则剩下的形状是(n-1)边形.所以遇到相关题目时,要分类讨论.
热考题型
考点四 多边形的内角和与外角和
6.(22-23七年级下·福建泉州·期末)正四边形与其他正多边形组合可以铺设地板,则该多边形可以是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【详解】解:A.正五边形每个内角108°,正四边形每个内角90°,显然不能组合成360°,所以不能铺设地板,不符合题意;
B.正六边形每个内角120°,正四边形每个内角90°,不能组合成360°,所以不能铺设地板,不符合题意;
C.正四边形每个内角90°,正八边形每个内角135°,90°+135°×2=360°,所以能铺设地板,符合题意;
D.因为十边形的每个内角是144°,正四边形的每个内角是90°,不能组合成360°,所以不能铺设地板,不符合题意;故选:C.
?
【解题技巧】解决几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
谢谢!
同课章节目录
