专题01 数据的收集、整理、描述与认识概率【考点串讲】课件(共30张PPT)-八年级数学下学期期中考点大串讲(苏科版)
文档属性
| 名称 | 专题01 数据的收集、整理、描述与认识概率【考点串讲】课件(共30张PPT)-八年级数学下学期期中考点大串讲(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 20:38:27 | ||
图片预览








文档简介
八年级苏科版数学下册期中考点大串讲
串讲01 数据的收集、整理、
描述与认识概率
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
考点一 数据的收集、整理、描述
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
概念
优缺点
全面调查
(普查)
为特定的目的对全部考察对象进行的调查,叫做全面调查.
优点:收集到的数据全面、准确
缺点:一般花费多、工作量大,耗时长
?
?
抽样调查
抽取一部分对象进行调查,根据调查样本数据推断全体对象的情况叫抽样调查.
优点:调查范围小,花费少、工作量较小,省时.
缺点:抽取的样本是否具有代表性,直接关系到对总体估计的准确程度.
【使用抽象调查时的注意事项】抽样时注意样本的代表性和广泛性.
【小技巧】一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.所以要根据调查目的、调查对象等因素,合理选择调查方法,不能凭主观臆想随意选择.
知识大全
考点一 数据的收集、整理、描述
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分类
概念
注意事项
总体
所要调查对象的全体对象叫做总体.
考察一个班学生的身高,那么总体就是指这个班学生身高的全体,不能错误地理解为学生的全体为总体.
个体
总体中的每一个考察对象叫做个体.
总体包括所有的个体.
样本
从总体中抽取的部分个体叫做样本.
样本是总体的一部分,一个总体中可以有许多样本,样本能够在一定程度上反映总体.
样本容量
样本中个体的数目称为样本容量.(无单位)
一般地,样本容量越大,通过样本对总体的估计越精确.
知识大全
考点一 数据的收集、整理、描述
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}统计图
图形
优点
缺点
常见结论
条形统计图
1)能清楚地表示出每个项目中的具体数目.
2)易于比较数目之间的差别.
对于条形统计图,人们习惯于由条形柱的高度看相应的数据,即条形柱的高度与相应的数据成正比,若条形柱的高度与数据不成正比,就容易给人造成错觉.
各组数量之和=总数
扇形统计图
能清楚地表示出各部分在总体中所占的百分比.
在两个扇形统计图中,若一个统计图中的某一个量所占的百分比比另一个统计图中的某个量所占的百分比多,这样容易造成第一个统计量比第二个统计量大的错误理解.
各部分百分比之和=100%;
?
各部分圆心角的度数=相应百分比×360°
知识大全
考点一 数据的收集、整理、描述
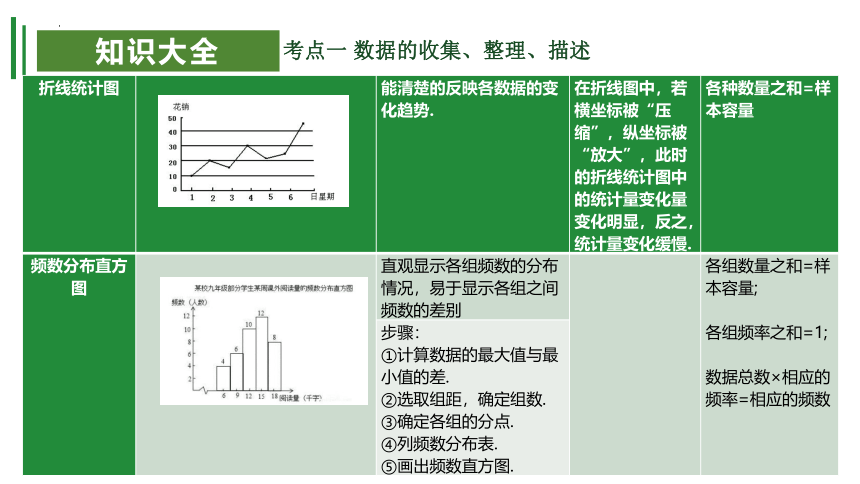
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}折线统计图
能清楚的反映各数据的变化趋势.
?
在折线图中,若横坐标被“压缩”,纵坐标被“放大”,此时的折线统计图中的统计量变化量变化明显,反之,统计量变化缓慢.
各种数量之和=样本容量
频数分布直方图
直观显示各组频数的分布情况,易于显示各组之间频数的差别
?
各组数量之和=样本容量;
?
各组频率之和=1;
?
数据总数×相应的频率=相应的频数
步骤:
①计算数据的最大值与最小值的差.
②选取组距,确定组数.
③确定各组的分点.
④列频数分布表.
⑤画出频数直方图.
易错易混
考点一 数据的收集、整理、描述
1. 条形统计图中每个小长方形的高即为该组对象数据的个数(频数),各小长方形的高之比等于相应的个数(频数)之比.
2. 扇形统计图中,用圆代表总体,扇形的大小代表各部分数量占总体数量的百分数,但是没有给出具体数值,因此不能通过两个扇形统计图来比较两个统计量的多少.
3. 在利用折线统计图比较两个统计量的变化趋势时,要保证两个图中横、纵坐标的一致性,即坐标轴上同一单位长度所表示的意义应该一致.
4. 画频数分布直方图时,分组要遵循三个原则:不空,即该组必须有数据;不重,即一个数据只能在一个组;不漏,即不能漏掉某一个数据.
热考题型
考点一 数据的收集、整理、描述
1.(23-24八年级上·重庆万州·期末)万州区教师进修学院为了督查国家双减政策的落实情况,现调查某校学生每日睡眠时长问题,选用下列哪种方法最恰当(????)
A.查阅文献资料 B.对学生问卷调查 C.上网查询 D.对校领导问卷调查
2.(23-24八年级上·河南开封·期末)某数学小组想了解本校1800余名学生对数学的喜爱情况,现拟定以下步骤进行调查:①从每班随机抽取10人进行调查;②设计对数学喜爱情况的调查问卷;③利用样本估计总体得出调查结论;④对得到结果进行记录整理.其中排序正确的是(????)
A.①②③④ B.②①④③ C.②①③④ D.①④②③
热考题型
考点一 数据的收集、整理、描述
3.(23-24八年级上·福建厦门·期中)下面调查方式中,合适的是(????)
A.调查长江的水质情况,采用抽样调查的方式
B.调查你所在班级同学的视力情况,采用抽样调查的方式
C.要了解全市初中学生的业余爱好,采用全面调查的方式
D.调查某栏目的收视率,采用全面调查的方式
4(23-24八年级上·江苏泰州·期末)为了了解兴化市八年级12000名学生的体重情况,从中抽查了700名学生的体重,就这个问题来说,下列说法正确的是(????)
A.12000名学生是总体 B.每个学生是个体
C.700名学生是所抽取的一个样本 D.样本容量为700
5.(19-20七年级下·湖南长沙·期末)今年某市有3万名学生参加了关于“你喜爱的一项体育运动”的问卷调查,从中抽取3000名学生的调查结果进行统计分析,以下说法错误的是(????)
A.3万名学生的问卷调查结果是总体 B.3000名学生的问卷调查结果是样本
C.3000名学生是样本容量 D.每一名学生的问卷调查结果是个体
?
热考题型
考点一 数据的收集、整理、描述
6.(22-23八年级下·江苏常州·期中)“2001年4月1日,王伟驾驶编号81192战机,面对美国侦察机的侵犯,用生命勇敢捍卫祖国南海领空,22年过去了,我们不会忘记,81192,收到请返航!”为了了解荣成市中学生对该历史事件的知晓情况,分别做了下列三种不同的抽样调查:①随机调查了荣成市1000名初三学生对该历史事件的知晓情况;②调查了荣成市实验中学全体学生对该历史事件的知晓情况;③利用荣成市学籍库随机调查了10%的中学生对该历史事件的知晓情况,你认为抽样最合理的是 (填序号).
【详解】解:随机调查了荣成市1000名初三学生对该历史事件的知晓情况;调查不具代表性,故①不合题意;
调查了荣成市实验中学全体学生对该历史事件的知晓情况;调查不具广泛性,故②不合题意;
利用荣成市学籍库随机调查了10%的中学生对该历史事件的知晓情况.调查具有广泛性、代表性,故③符合题意;
故答案为:③
热考题型
考点一 数据的收集、整理、描述
7.(22-23·河北 邯郸·期中)如图,根据条形图所提供的信息,请指出以下四种答案中哪一个是正确的(????)
A.8年级学生最少 B.9年级的男生是女生的两倍
C.10年级学生女生比男生多 D.8年级和10年级的学生一样多
【详解】根据图中数据计算:七年级人数是8+13=21;八年级人数是14+16=30;九年级人数是10+20=30,十年级人数是14+18=32,所以A和D错误;
根据统计图的高低,显然10年级学生女生比男生少,故C错误;
B中,九年级的男生20人是女生10人的两倍,正确.
故选B.
?
热考题型
考点一 数据的收集、整理、描述
7.(23-24七年级上·广东佛山·期中)南海图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有45本,则丙类书的本数是(????)
A.90 B.120 C.180 D.200
【详解】解:课外书籍的总本数是45÷15%=300,
则丙类书的本数是300×1?15%?45%=120,故选:B.
?
8.(2023·吉安·三模)随着初中学业水平考试的临近,某校连续四个月开展了学科知识模拟测试,并将测试成绩进行整理,最终绘制了如图所示的统计图(四次参加模拟测试的学生人数不变)下列四个结论中不正确的是(????)
A.共有500名学生参加模拟测试
B.从第1个月到第4个月,测试成绩为“优秀”的学生人数在总人数中的占比逐渐增长
C.第2个月测试成绩为“优秀”的学生达到50人
D.第4个月增长的“优秀”人数比第3个月增长的“优秀”人数少
热考题型
考点一 数据的收集、整理、描述
9.(22-23八年级下·江苏盐城·期中)吾悦广场开了一家特色美食店,开业一周后老板计划用统计图直观反映这周各天收入的起伏情况,下列各统计图中你认为最优的选择是(??)
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
10.(21-22七年级下·吉林长春·期中)为了直观地表示世界七大洲的面积各占全球陆地面积的百分比,最适合使用的统计图是 统计图.
11.(20-21八年级上·重庆沙坪坝·期末)一个班有40名学生,在一次身体素质测试中,将全班学生的测试结果分为优秀、合格、不合格.测试结果达到优秀的有18人,合格的有17人,则在这次测试中,测试结果不合格的频率是( )
A.0.125 B.0.30 C.0.45 D.1.25
扇形
【详解】解:不合格人数为40?18?17=5(人),
∴不合格人数的频率是540=0.125,故选:A.
?
12.(23-24八年级上·江苏宿迁·期末)阅读是人类获取知识、启智增慧、培养道德的重要途径,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读的时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
??
根据以上信息,解答下列问题:
(1)在这次抽样调查中,样本容量是______;
(2)请补全频数分布直方图,并计算在扇形统计图中B类所对应扇形的圆心角的度数;
热考题型
考点一 数据的收集、整理、描述
【详解】(1)解:由图表可知,40÷40%=100(名),
所以这次抽样调查中,样本容量是100,
故答案为:100.
?
12.(23-24八年级上·江苏宿迁·期末)阅读是人类获取知识、启智增慧、培养道德的重要途径,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读的时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
??
根据以上信息,解答下列问题:
(1)在这次抽样调查中,样本容量是______;
(2)请补全频数分布直方图,并计算在扇形统计图中B类所对应扇形的圆心角的度数;
热考题型
考点一 数据的收集、整理、描述
(2)解:由题知,100?5?40?25=30(名),
补全频数分布直方图如下:
360°×30100=108°,所以B类所对应扇形的圆心角度数为108°.
?
12.(23-24八年级上·江苏宿迁·期末)阅读是人类获取知识、启智增慧、培养道德的重要途径,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读的时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
??
根据以上信息,解答下列问题:
(1)在这次抽样调查中,样本容量是______;
(2)请补全频数分布直方图,并计算在扇形统计图中B类所对应扇形的圆心角的度数;
(3)若该校有1200名学生,试估计该校学生近两周平均每天在家阅读时长不足1个小时的人数.
热考题型
考点一 数据的收集、整理、描述
(3)解:1200×5+30100=420(名),
答:该校学生近两周平均每天在家阅读时长不足1个小时有420人.
?
热考题型
考点一 数据的收集、整理、描述
13.(22-23八年级下·江西南昌·期末)夏季来临,为了进一步增强广大学生预防溺水安全教育的意识,某校举行了防溺水安全知识竞赛,测试满分为100分,随机在八年级抽取了10名参赛学生成绩,已知抽到的八年级的竞赛成绩(单位:分)如下:80,95,100,85,75,85,90,85,70,85.
(1)请你求出以上10名同学成绩的众数;
(2)请你给广大同学提三条预防溺水的建议.
?
【详解】(1)解: 85分出现的次数最多,为4次,众数为85(分);
(2)预防溺水的建议:不私自下水游泳;不擅自与他人结伴游泳;
不在无家长或老师带队的情况下游泳;不到不熟悉的水域游泳;不到无安全设施、无救护人员的水域游泳;
不准不会水性的学生擅自下水施救.
?
知识大全
考点二 认识概率
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义
事件发生的概率
确定事件
必然
事件
在一定条件下,有些事情我们事先肯定它一定发生,这些事情称为必然事件。
P(必然事件)=1
?
不可能事件
在一定条件下,有些事情我们事先肯定它一定不会发生,这些事情称为不可能事件。
P(不可能事件)=0
不确定事件(随机事件)
在一定条件下,许多事情我们无法确定它会不会发生,这些事情称为不确定事件(又叫随机事件)。
0<P(随机事件)<1
解题技巧
考点二 认识概率
判断事件发生的可能性大小,首先看是什么事件,必然事件的可能性最大为100%,不可能事件的可能性最小为0,随机事件的可能性有大有小,其发生可能性介于0-100%.在随机事件中,要想判断随机事件发生的概率就要列举出随机事件中可能出现的各种结果,其中包含的结果数多的事件发生的可能性大.所以平时要多加练习如何列举全随机事件中包含的各种结果,如果少列举一种都会造成错误结果.
解题技巧
考点二 认识概率
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性. 因此可以用随机事件发生的频率来估计该事件发生的概率.
适用范围:当实验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.
热考题型
考点二 认识概率
1.(23-24八年级上·江苏泰州·期末)下列事件中是确定事件的是( )
A.14人中至少有2人在同一个月过生日 B.小明投篮一次得3分
C.一个月有30天 D.小林参加马拉松比赛,成绩是第一名
2.(23-24八年级上·北京昌平·期末)下列事件中,属于随机事件的是( )
A.李叔叔以家庭主申请人的身份申请北京市小客车指标,在提交申请后的第一次“摇号”就中签
B.直角三角形两锐角互余
C.第一小组的10名同学中,包含了3名女生,若从这组选出4名同学完成任务,则至少有1名男生
D.掷一枚标准的骰子,面朝上的点数等于8
热考题型
考点二 认识概率
2.(22-23八年级下·江苏南京·期中)八年级(1)班有40位同学,他们的学号是1?40,随机抽取一名学生参加座谈会,下列事件:①抽到的学号为奇数;②抽到的学号是个位数;③抽到的学号不小于35.其中,发生可能性最小的事件为 (填序号).
?
【详解】解:①抽到的学号是奇数的可能性为2040=12;
②抽到的学号是个位数的可能性为940;
③抽到的学号不小于35的可能性为640=320,
∵320<940<12,
∴发生可能性最小的事件为为③,
故答案为:③.
?
热考题型
考点二 认识概率
3.(20-21八年级下·江苏常州·期中)一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,将球搅匀,从中任意摸出1个球.
(1)会出现哪些可能的结果?
(2)能够事先确定摸到的一定是红球吗?
(3)你认为摸到哪种颜色的球的可能性最大?哪种颜色的球的可能性最小?
(4)怎样改变袋子中红球、绿球、白球的个数,使摸到这三种颜色的球的概率相同?
?
【详解】解:(1)从中任意摸出1个球可能是红球,也可能是绿球或白球;
(2)不能事先确定摸到的一定是红球;
(3)摸到白球的可能性最大,摸到红球的可能性最小;
(4)只要袋子中红球、绿球和白球的数量相等即可.
热考题型
考点二 认识概率
4(22-23八年级下·江苏泰州·期末)袋中装有8个小球,颜色为红、白、黑,每个球除颜色外其它都相同,将球摇匀,从中任意摸出一个球,若要求摸出的球是黑球和不是黑球的可能性一样,则红球和白球共有 个.
【详解】解:若要求摸出的球是黑球和不是黑球的可能性一样,则黑球占12;
红球和白球共占12.
故红球和白球共有12×8=4个.
故答案为:4.
?
热考题型
考点二 认识概率
5.(20-21九年级上·河南洛阳·期末)下列说法错误的是(???)
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件在试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
6.(20-21九年级上·陕西西安·阶段练习)抛掷一枚质地均匀的硬币,“反面朝上”的概率为0.5,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是(????)
A.可能有50次反面朝上 B.每两次必有1次反面朝上
C.必有50次反面朝上 D.不可能有100次反面朝上
【解题技巧】概率是频率的稳定值,频率是概率的近似值,且随实验次数的增多,值越来越精确.
热考题型
考点二 认识概率
7.(22-23八年级下·河北沧州·阶段练习)在一个样本中,50个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5,则第4小组的频率是(????)
A.0.15 B.0.2 C.0.3 D.0.4
?
【详解】解:50个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5,
∴第4小组的频数为50?2?8?15?5=20,∴第4小组频率为20÷50=0.4,故选:D.
?
8.(22-23八年级下·江苏盐城·期中)期中调研日期为“2023年04月20日”,其中出现的频率相同的数字是(????)
A.0和4 B.0和3 C.2和4 D.0和2
【详解】解:在“2023年04月20日”中,共有0、2、3、4四个数字,其中0出现了3次,2出现了3次,3出现了1次,4出现了1次,
则数字0和2的频率相同,均为33+3+1+1=0.375,
数字3和4的频率相同,均为13+3+1+1=0.125.
故选:D.
?
热考题型
考点二 认识概率
9.(22-23八年级下·江苏连云港·阶段练习)在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率稳定于0.25,
(1)请估计摸到白球的概率将会接近______;
(2)如果要使摸到白球的概率为25,需要往盒子里再放入多少个白球?
?
【详解】(1)经过大量重复上述摸球的过程,发现摸到白球的频率稳定于0.25;
∴估计摸到白球的概率将会接近0.25
故答案为:0.25.
?
热考题型
考点二 认识概率
9.(22-23八年级下·江苏连云港·阶段练习)在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率稳定于0.25,
(1)请估计摸到白球的概率将会接近______;
(2)如果要使摸到白球的概率为25,需要往盒子里再放入多少个白球?
?
(2)原有白球:60×0.25=15
设需要往盒子里再放入x个白球
根据题意得:15+????60+????=25,解得:????=15(经检验,????=15是原方程的解)
答:需要往盒子里再放入15个白球.
?
谢谢!
串讲01 数据的收集、整理、
描述与认识概率
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
考点一 数据的收集、整理、描述
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
概念
优缺点
全面调查
(普查)
为特定的目的对全部考察对象进行的调查,叫做全面调查.
优点:收集到的数据全面、准确
缺点:一般花费多、工作量大,耗时长
?
?
抽样调查
抽取一部分对象进行调查,根据调查样本数据推断全体对象的情况叫抽样调查.
优点:调查范围小,花费少、工作量较小,省时.
缺点:抽取的样本是否具有代表性,直接关系到对总体估计的准确程度.
【使用抽象调查时的注意事项】抽样时注意样本的代表性和广泛性.
【小技巧】一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.所以要根据调查目的、调查对象等因素,合理选择调查方法,不能凭主观臆想随意选择.
知识大全
考点一 数据的收集、整理、描述
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分类
概念
注意事项
总体
所要调查对象的全体对象叫做总体.
考察一个班学生的身高,那么总体就是指这个班学生身高的全体,不能错误地理解为学生的全体为总体.
个体
总体中的每一个考察对象叫做个体.
总体包括所有的个体.
样本
从总体中抽取的部分个体叫做样本.
样本是总体的一部分,一个总体中可以有许多样本,样本能够在一定程度上反映总体.
样本容量
样本中个体的数目称为样本容量.(无单位)
一般地,样本容量越大,通过样本对总体的估计越精确.
知识大全
考点一 数据的收集、整理、描述
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}统计图
图形
优点
缺点
常见结论
条形统计图
1)能清楚地表示出每个项目中的具体数目.
2)易于比较数目之间的差别.
对于条形统计图,人们习惯于由条形柱的高度看相应的数据,即条形柱的高度与相应的数据成正比,若条形柱的高度与数据不成正比,就容易给人造成错觉.
各组数量之和=总数
扇形统计图
能清楚地表示出各部分在总体中所占的百分比.
在两个扇形统计图中,若一个统计图中的某一个量所占的百分比比另一个统计图中的某个量所占的百分比多,这样容易造成第一个统计量比第二个统计量大的错误理解.
各部分百分比之和=100%;
?
各部分圆心角的度数=相应百分比×360°
知识大全
考点一 数据的收集、整理、描述
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}折线统计图
能清楚的反映各数据的变化趋势.
?
在折线图中,若横坐标被“压缩”,纵坐标被“放大”,此时的折线统计图中的统计量变化量变化明显,反之,统计量变化缓慢.
各种数量之和=样本容量
频数分布直方图
直观显示各组频数的分布情况,易于显示各组之间频数的差别
?
各组数量之和=样本容量;
?
各组频率之和=1;
?
数据总数×相应的频率=相应的频数
步骤:
①计算数据的最大值与最小值的差.
②选取组距,确定组数.
③确定各组的分点.
④列频数分布表.
⑤画出频数直方图.
易错易混
考点一 数据的收集、整理、描述
1. 条形统计图中每个小长方形的高即为该组对象数据的个数(频数),各小长方形的高之比等于相应的个数(频数)之比.
2. 扇形统计图中,用圆代表总体,扇形的大小代表各部分数量占总体数量的百分数,但是没有给出具体数值,因此不能通过两个扇形统计图来比较两个统计量的多少.
3. 在利用折线统计图比较两个统计量的变化趋势时,要保证两个图中横、纵坐标的一致性,即坐标轴上同一单位长度所表示的意义应该一致.
4. 画频数分布直方图时,分组要遵循三个原则:不空,即该组必须有数据;不重,即一个数据只能在一个组;不漏,即不能漏掉某一个数据.
热考题型
考点一 数据的收集、整理、描述
1.(23-24八年级上·重庆万州·期末)万州区教师进修学院为了督查国家双减政策的落实情况,现调查某校学生每日睡眠时长问题,选用下列哪种方法最恰当(????)
A.查阅文献资料 B.对学生问卷调查 C.上网查询 D.对校领导问卷调查
2.(23-24八年级上·河南开封·期末)某数学小组想了解本校1800余名学生对数学的喜爱情况,现拟定以下步骤进行调查:①从每班随机抽取10人进行调查;②设计对数学喜爱情况的调查问卷;③利用样本估计总体得出调查结论;④对得到结果进行记录整理.其中排序正确的是(????)
A.①②③④ B.②①④③ C.②①③④ D.①④②③
热考题型
考点一 数据的收集、整理、描述
3.(23-24八年级上·福建厦门·期中)下面调查方式中,合适的是(????)
A.调查长江的水质情况,采用抽样调查的方式
B.调查你所在班级同学的视力情况,采用抽样调查的方式
C.要了解全市初中学生的业余爱好,采用全面调查的方式
D.调查某栏目的收视率,采用全面调查的方式
4(23-24八年级上·江苏泰州·期末)为了了解兴化市八年级12000名学生的体重情况,从中抽查了700名学生的体重,就这个问题来说,下列说法正确的是(????)
A.12000名学生是总体 B.每个学生是个体
C.700名学生是所抽取的一个样本 D.样本容量为700
5.(19-20七年级下·湖南长沙·期末)今年某市有3万名学生参加了关于“你喜爱的一项体育运动”的问卷调查,从中抽取3000名学生的调查结果进行统计分析,以下说法错误的是(????)
A.3万名学生的问卷调查结果是总体 B.3000名学生的问卷调查结果是样本
C.3000名学生是样本容量 D.每一名学生的问卷调查结果是个体
?
热考题型
考点一 数据的收集、整理、描述
6.(22-23八年级下·江苏常州·期中)“2001年4月1日,王伟驾驶编号81192战机,面对美国侦察机的侵犯,用生命勇敢捍卫祖国南海领空,22年过去了,我们不会忘记,81192,收到请返航!”为了了解荣成市中学生对该历史事件的知晓情况,分别做了下列三种不同的抽样调查:①随机调查了荣成市1000名初三学生对该历史事件的知晓情况;②调查了荣成市实验中学全体学生对该历史事件的知晓情况;③利用荣成市学籍库随机调查了10%的中学生对该历史事件的知晓情况,你认为抽样最合理的是 (填序号).
【详解】解:随机调查了荣成市1000名初三学生对该历史事件的知晓情况;调查不具代表性,故①不合题意;
调查了荣成市实验中学全体学生对该历史事件的知晓情况;调查不具广泛性,故②不合题意;
利用荣成市学籍库随机调查了10%的中学生对该历史事件的知晓情况.调查具有广泛性、代表性,故③符合题意;
故答案为:③
热考题型
考点一 数据的收集、整理、描述
7.(22-23·河北 邯郸·期中)如图,根据条形图所提供的信息,请指出以下四种答案中哪一个是正确的(????)
A.8年级学生最少 B.9年级的男生是女生的两倍
C.10年级学生女生比男生多 D.8年级和10年级的学生一样多
【详解】根据图中数据计算:七年级人数是8+13=21;八年级人数是14+16=30;九年级人数是10+20=30,十年级人数是14+18=32,所以A和D错误;
根据统计图的高低,显然10年级学生女生比男生少,故C错误;
B中,九年级的男生20人是女生10人的两倍,正确.
故选B.
?
热考题型
考点一 数据的收集、整理、描述
7.(23-24七年级上·广东佛山·期中)南海图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有45本,则丙类书的本数是(????)
A.90 B.120 C.180 D.200
【详解】解:课外书籍的总本数是45÷15%=300,
则丙类书的本数是300×1?15%?45%=120,故选:B.
?
8.(2023·吉安·三模)随着初中学业水平考试的临近,某校连续四个月开展了学科知识模拟测试,并将测试成绩进行整理,最终绘制了如图所示的统计图(四次参加模拟测试的学生人数不变)下列四个结论中不正确的是(????)
A.共有500名学生参加模拟测试
B.从第1个月到第4个月,测试成绩为“优秀”的学生人数在总人数中的占比逐渐增长
C.第2个月测试成绩为“优秀”的学生达到50人
D.第4个月增长的“优秀”人数比第3个月增长的“优秀”人数少
热考题型
考点一 数据的收集、整理、描述
9.(22-23八年级下·江苏盐城·期中)吾悦广场开了一家特色美食店,开业一周后老板计划用统计图直观反映这周各天收入的起伏情况,下列各统计图中你认为最优的选择是(??)
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
10.(21-22七年级下·吉林长春·期中)为了直观地表示世界七大洲的面积各占全球陆地面积的百分比,最适合使用的统计图是 统计图.
11.(20-21八年级上·重庆沙坪坝·期末)一个班有40名学生,在一次身体素质测试中,将全班学生的测试结果分为优秀、合格、不合格.测试结果达到优秀的有18人,合格的有17人,则在这次测试中,测试结果不合格的频率是( )
A.0.125 B.0.30 C.0.45 D.1.25
扇形
【详解】解:不合格人数为40?18?17=5(人),
∴不合格人数的频率是540=0.125,故选:A.
?
12.(23-24八年级上·江苏宿迁·期末)阅读是人类获取知识、启智增慧、培养道德的重要途径,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读的时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
??
根据以上信息,解答下列问题:
(1)在这次抽样调查中,样本容量是______;
(2)请补全频数分布直方图,并计算在扇形统计图中B类所对应扇形的圆心角的度数;
热考题型
考点一 数据的收集、整理、描述
【详解】(1)解:由图表可知,40÷40%=100(名),
所以这次抽样调查中,样本容量是100,
故答案为:100.
?
12.(23-24八年级上·江苏宿迁·期末)阅读是人类获取知识、启智增慧、培养道德的重要途径,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读的时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
??
根据以上信息,解答下列问题:
(1)在这次抽样调查中,样本容量是______;
(2)请补全频数分布直方图,并计算在扇形统计图中B类所对应扇形的圆心角的度数;
热考题型
考点一 数据的收集、整理、描述
(2)解:由题知,100?5?40?25=30(名),
补全频数分布直方图如下:
360°×30100=108°,所以B类所对应扇形的圆心角度数为108°.
?
12.(23-24八年级上·江苏宿迁·期末)阅读是人类获取知识、启智增慧、培养道德的重要途径,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读的时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
??
根据以上信息,解答下列问题:
(1)在这次抽样调查中,样本容量是______;
(2)请补全频数分布直方图,并计算在扇形统计图中B类所对应扇形的圆心角的度数;
(3)若该校有1200名学生,试估计该校学生近两周平均每天在家阅读时长不足1个小时的人数.
热考题型
考点一 数据的收集、整理、描述
(3)解:1200×5+30100=420(名),
答:该校学生近两周平均每天在家阅读时长不足1个小时有420人.
?
热考题型
考点一 数据的收集、整理、描述
13.(22-23八年级下·江西南昌·期末)夏季来临,为了进一步增强广大学生预防溺水安全教育的意识,某校举行了防溺水安全知识竞赛,测试满分为100分,随机在八年级抽取了10名参赛学生成绩,已知抽到的八年级的竞赛成绩(单位:分)如下:80,95,100,85,75,85,90,85,70,85.
(1)请你求出以上10名同学成绩的众数;
(2)请你给广大同学提三条预防溺水的建议.
?
【详解】(1)解: 85分出现的次数最多,为4次,众数为85(分);
(2)预防溺水的建议:不私自下水游泳;不擅自与他人结伴游泳;
不在无家长或老师带队的情况下游泳;不到不熟悉的水域游泳;不到无安全设施、无救护人员的水域游泳;
不准不会水性的学生擅自下水施救.
?
知识大全
考点二 认识概率
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义
事件发生的概率
确定事件
必然
事件
在一定条件下,有些事情我们事先肯定它一定发生,这些事情称为必然事件。
P(必然事件)=1
?
不可能事件
在一定条件下,有些事情我们事先肯定它一定不会发生,这些事情称为不可能事件。
P(不可能事件)=0
不确定事件(随机事件)
在一定条件下,许多事情我们无法确定它会不会发生,这些事情称为不确定事件(又叫随机事件)。
0<P(随机事件)<1
解题技巧
考点二 认识概率
判断事件发生的可能性大小,首先看是什么事件,必然事件的可能性最大为100%,不可能事件的可能性最小为0,随机事件的可能性有大有小,其发生可能性介于0-100%.在随机事件中,要想判断随机事件发生的概率就要列举出随机事件中可能出现的各种结果,其中包含的结果数多的事件发生的可能性大.所以平时要多加练习如何列举全随机事件中包含的各种结果,如果少列举一种都会造成错误结果.
解题技巧
考点二 认识概率
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性. 因此可以用随机事件发生的频率来估计该事件发生的概率.
适用范围:当实验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.
热考题型
考点二 认识概率
1.(23-24八年级上·江苏泰州·期末)下列事件中是确定事件的是( )
A.14人中至少有2人在同一个月过生日 B.小明投篮一次得3分
C.一个月有30天 D.小林参加马拉松比赛,成绩是第一名
2.(23-24八年级上·北京昌平·期末)下列事件中,属于随机事件的是( )
A.李叔叔以家庭主申请人的身份申请北京市小客车指标,在提交申请后的第一次“摇号”就中签
B.直角三角形两锐角互余
C.第一小组的10名同学中,包含了3名女生,若从这组选出4名同学完成任务,则至少有1名男生
D.掷一枚标准的骰子,面朝上的点数等于8
热考题型
考点二 认识概率
2.(22-23八年级下·江苏南京·期中)八年级(1)班有40位同学,他们的学号是1?40,随机抽取一名学生参加座谈会,下列事件:①抽到的学号为奇数;②抽到的学号是个位数;③抽到的学号不小于35.其中,发生可能性最小的事件为 (填序号).
?
【详解】解:①抽到的学号是奇数的可能性为2040=12;
②抽到的学号是个位数的可能性为940;
③抽到的学号不小于35的可能性为640=320,
∵320<940<12,
∴发生可能性最小的事件为为③,
故答案为:③.
?
热考题型
考点二 认识概率
3.(20-21八年级下·江苏常州·期中)一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,将球搅匀,从中任意摸出1个球.
(1)会出现哪些可能的结果?
(2)能够事先确定摸到的一定是红球吗?
(3)你认为摸到哪种颜色的球的可能性最大?哪种颜色的球的可能性最小?
(4)怎样改变袋子中红球、绿球、白球的个数,使摸到这三种颜色的球的概率相同?
?
【详解】解:(1)从中任意摸出1个球可能是红球,也可能是绿球或白球;
(2)不能事先确定摸到的一定是红球;
(3)摸到白球的可能性最大,摸到红球的可能性最小;
(4)只要袋子中红球、绿球和白球的数量相等即可.
热考题型
考点二 认识概率
4(22-23八年级下·江苏泰州·期末)袋中装有8个小球,颜色为红、白、黑,每个球除颜色外其它都相同,将球摇匀,从中任意摸出一个球,若要求摸出的球是黑球和不是黑球的可能性一样,则红球和白球共有 个.
【详解】解:若要求摸出的球是黑球和不是黑球的可能性一样,则黑球占12;
红球和白球共占12.
故红球和白球共有12×8=4个.
故答案为:4.
?
热考题型
考点二 认识概率
5.(20-21九年级上·河南洛阳·期末)下列说法错误的是(???)
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件在试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
6.(20-21九年级上·陕西西安·阶段练习)抛掷一枚质地均匀的硬币,“反面朝上”的概率为0.5,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是(????)
A.可能有50次反面朝上 B.每两次必有1次反面朝上
C.必有50次反面朝上 D.不可能有100次反面朝上
【解题技巧】概率是频率的稳定值,频率是概率的近似值,且随实验次数的增多,值越来越精确.
热考题型
考点二 认识概率
7.(22-23八年级下·河北沧州·阶段练习)在一个样本中,50个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5,则第4小组的频率是(????)
A.0.15 B.0.2 C.0.3 D.0.4
?
【详解】解:50个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5,
∴第4小组的频数为50?2?8?15?5=20,∴第4小组频率为20÷50=0.4,故选:D.
?
8.(22-23八年级下·江苏盐城·期中)期中调研日期为“2023年04月20日”,其中出现的频率相同的数字是(????)
A.0和4 B.0和3 C.2和4 D.0和2
【详解】解:在“2023年04月20日”中,共有0、2、3、4四个数字,其中0出现了3次,2出现了3次,3出现了1次,4出现了1次,
则数字0和2的频率相同,均为33+3+1+1=0.375,
数字3和4的频率相同,均为13+3+1+1=0.125.
故选:D.
?
热考题型
考点二 认识概率
9.(22-23八年级下·江苏连云港·阶段练习)在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率稳定于0.25,
(1)请估计摸到白球的概率将会接近______;
(2)如果要使摸到白球的概率为25,需要往盒子里再放入多少个白球?
?
【详解】(1)经过大量重复上述摸球的过程,发现摸到白球的频率稳定于0.25;
∴估计摸到白球的概率将会接近0.25
故答案为:0.25.
?
热考题型
考点二 认识概率
9.(22-23八年级下·江苏连云港·阶段练习)在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率稳定于0.25,
(1)请估计摸到白球的概率将会接近______;
(2)如果要使摸到白球的概率为25,需要往盒子里再放入多少个白球?
?
(2)原有白球:60×0.25=15
设需要往盒子里再放入x个白球
根据题意得:15+????60+????=25,解得:????=15(经检验,????=15是原方程的解)
答:需要往盒子里再放入15个白球.
?
谢谢!
同课章节目录
