专题03 分式【考点串讲】课件(共31张PPT) -八年级数学下学期期中考点大串讲(苏科版)
文档属性
| 名称 | 专题03 分式【考点串讲】课件(共31张PPT) -八年级数学下学期期中考点大串讲(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 20:57:23 | ||
图片预览










文档简介
八年级苏科版数学下册期中考点大串讲
串讲03 分式
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
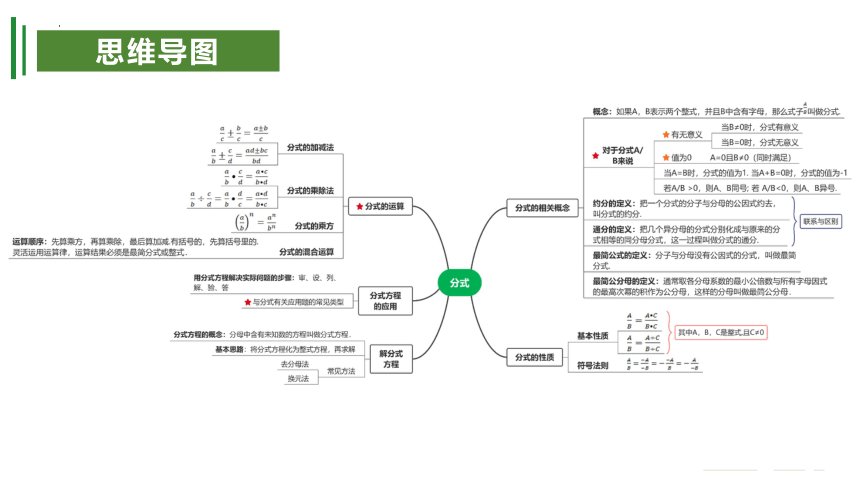
思维导图
知识大全
考点一 分式的运算
分式的概念:如果A,B表示两个整式,并且B中含有字母,那么式子AB叫做分式,A为分子,B为分母.
对于分式AB来说: ①当B≠0时,分式有意义;当 B=0时,分式无意义.
②当A=0且B≠0这两个条件同时满足时,分式值为0.
③当A=B时,分式的值为1.当A+B=0时,分式的值为-1.
④若AB>0,则A、B同号; 若AB<0,则A、B异号.
约分的定义:把一个分式的分子与分母的公因式约去,叫分式的约分.
最简公式的定义:分子与分母没有公因式的分式,叫做最简分式.
通分的定义:把几个异分母的分式分别化成与原来的分式相等的同分母分式,这一过程叫做分式的通分.
通分步骤:①定最简公分母;②化异分母为最简公分母.
最简公分母的定义:通常取各分母系数的最小公倍数与所有字母因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
?
解题技巧
考点一 分式的基础
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类型
确定最简公分母的方法
?
分母为单项式
1)取单项式中所有系数的最小公倍数作为最简公分母的系数;
2)取单项式中每个字母出现的最高次数作为最简公分母中该字母的次数.
?
分母为多项式
1)对每个分母因式分解;
2)找出每个出现的因式的最高次幂,它们的积为最简公分母;
3) 若有系数,求各分母系数的最小公倍数作为最简公分母的系数.
知识大全
考点一 分式的基础
分式的基本性质:分式的分子和分母同乘(或除以)一个不等于0的整式,分式的值不变. 即:AB=A?CB?C(C≠0)或AB=A÷CB÷C(C≠0),其中A,B,C是整式.
分式符号法则:分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变,即:AB=?A?B=??AB=?A?B.
?
知识大全
考点一 分式的基础
热考题型
考点一 分式的基础
1.(23-24八年级下·河南南阳·阶段练习)在代数式?????????????,????2,2????+3,13????+????中,属于分式的有(???)
A.1个 B.2个 C.3个 D.4个
?
2.(23-24八年级下·全国·课后作业)若代数式?????2?????3有意义,则x的取值范围是( )
A.????>2且????≠3 B.????≥2
C.????≠3 D.????≥2且????≠3
?
3.(21-22八年级上·贵州铜仁·期末)下列关于分式的判断,正确的是(????)
A.当????=2时,????+1?????2的值为0
B.当????≠3时,?????3????有意义
C.无论x为何值,3????+1的值不可能是正整数
D.无论x为何值,1????2+1总有意义
?
【详解】解:A.当????=2时,分式????+1?????2无意义,故该选项错误,不符合题意;
B.当????=0时,分式?????3????无意义,故该选项错误,不符合题意;
C.当????=2时,分式3????+1=1,为正整数,故该选项错误,不符合题意;
D.因为无论x为何值????2+1≥1,即????2+1≠0,
所以分式1????2+1总有意义,故该选项正确,符合题意.
故选D.
?
热考题型
考点一 分式的基础
4.(23-24八年级上·山东临沂·期末)已知????2??????6=0,则2????????2+3?????6的值是(????)
A.13 B.12 C.23 D.1
5.(23-24八年级上·湖南长沙·阶段练习)若分式2????+1????2的值为正,则????的取值范围是(??? )
A.????>0 B.????>?12 C.????≠?12 D.????>?12且????≠0
?
【详解】解:∵????2??????6=0,∴????2?????=6,
∴2????????2+3?????6=2????????2?????+4?????6=2????6+4?????6=2????4????=12,故选:B.
?
【详解】解:由题意得,????2>0,且????≠0,
∵分式2????+1????2的值为正,∴2????+1>0,
∴????>?12,∴????>?12且????≠0.
故选:D.
?
热考题型
考点一 分式的基础
6.(23-24八年级上·全国·课后作业)(1)当????取什么值时,分式????+13?????2有意义?
(2)当????取什么值时,分式?15?????的值为负?
(3)当????取什么值时,分式?????21+????2的值为负?
(4)当????取什么值时,分式????2?1????+1的值为0?
?
【详解】解:(1)∵分式????+13?????2有意义∴3?????2≠0,解得:????≠23;
(2)∵分式?15?????的值为负∴5?????>0,∴????<5;
(3)∵分式?????21+????2的值为负∴1+????2>0且?????2<0,??∴????≠0;
(4)∵分式????2?1????+1的值为0,∴????2?1=0且????+1≠0,解得:????=1
?
热考题型
考点一 分式的基础
7.(23-24八年级上·黑龙江牡丹江·期末)观察下列关于????的分式,探究其规律:2????,5????3,8????5,11????7,?,按着上述规律,第????个分式是 .
?
【详解】解:根据分式的分子和分母的规律可得,第????个分式是3?????1????2?????1.
?
8.(23-24八年级下·江苏泰州·阶段练习)计算.
(1)约分:????2+4????????+4????2????2?4????2 ;
(2)通分:????????2?????????,?????????????2+????????.
?
【详解】(1)????2+4????????+4????2????2?4????2=????+2????2????+2?????????2????=????+2?????????2????;
(2)∵????????2?????????=?????????????????,?????????????2+????????=?????????????????+????
∴????????2?????????=?????????????????+????=??????+?????????????????????+????,
?????????????2+????????=?????????????????+????=??????????????????????????+?????????????=?????????2????????+?????????????,
?
热考题型
考点一 分式的基础
9.(21-22八年级下·陕西咸阳·阶段练习)下列各选项中,所求的最简公分母错误的是(????)
A.12????与13????的最简公分母是6????
B.12????2????与2????????3????的最简公分母是2????2????????
C.1????2?4与1????+2的最简公分母是????+2?????2
D.????3?????3????与?????????????的最简公分母是3?????????
?
【详解】解:12????与13????的最简公分母是6????,故A正确,不符合题意,
12????2????与2????????3????的最简公分母是2????2????3????,故B错误,符合题意,
1????2?4与1????+2的最简公分母是????+2?????2,故C正确,不符合题意,
????3?????3????与?????????????的最简公分母是3?????????,故D正确,不符合题意,
故选:B.
?
热考题型
考点一 分式的基础
10.(23-24八年级下·全国·课后作业)下列各式:①?????????????+????;②???????????????????;③???????????????????;④????????????????????.其中与?????????????+????相等的是( )
A.①②③ B.②③④ C.②③ D.③④
11.【热考易错】(23-24八年级下·江苏连云港·阶段练习)将分式?????3????????????中的m、n同时扩大为原来的3倍,分式的值将(????)
A.扩大3倍 B.不变 C.缩小为原来的13 D.缩小为原来的19
12.(23-24八年级上·全国·课堂例题)不改变分式的值,把分式12?????0.7????0.3????+????的分子与分母的各项系数化为整数为 .
?
【详解】解:12?????0.7????0.3????+????=0.5?????0.7????0.3????+????将分子、分母同时扩大10倍,不改变分式的值10×0.5?????0.7????10×0.3????+????=5?????7????3????+10????
?
热考题型
考点一 分式的基础
13.(22-23七年级上·上海黄浦·期中)已如3????2?7????+2?????1????+1=3+?????????1+????????+1是恒等式,请分别求的a、b的值.
?
【详解】解:3????2?7????+2?????1????+1=3+?????????1+????????+1,
∴去分母可得:3????2?7????+2=3????+1?????1+????????+1+?????????1,
∴3????2?7????+2=3????2+????+????????+??????????3,
由恒等式可得:????+????=?7??????????3=2,解得:????=?1????=?6.
?
热考题型
考点一 分式的基础
14.(23-24八年级下·江苏镇江·阶段练习)计算
(1)2????+3????+1?????+2????+1
(2)????2????2??????????????22????
(3)25?????2????2+10????+25÷????2?1????+5?????2+2????+1?????5
(4)?????3?????2÷????+2?5?????2
?
【详解】(1)解:原式=2????+3?????+2????+1=2????+3??????2????+1=????+1????+1=1;
(2)解:原式=?????2????2?????????????22????=?????????2????;
(3)解:原式=5?????5+????????+52÷?????1????+1????+5?????+12?????5=5?????5+????????+52?????+5?????1????+1?????+12?????5=?????+1?????1;
(4)解:原式=?????3?????2÷????2?4?????2?5?????2=?????3?????2÷????2?4?5?????2=?????3?????2÷????2?9?????2=?????3?????2÷?????3????+3?????2=?????3?????2??????2?????3????+3=1????+3.
?
热考题型
考点一 分式的基础
15.(23-24八年级下·河南南阳·阶段练习)先化简????2????+2?????+2÷4????????2?4,然后从?6?
【详解】解:????2????+2?????+2÷4????????2?4=????2?????2?2????+2????+4????+2÷4????????+2?????2=4????+2?????+2?????24????=?????2????,
∵分式要有意义,
∴????+2?????2≠0????≠0,
∴????≠±2且????≠0,
∵?6∴当????=1时,原式=1?21=?1;当????=?1时,原式=?1?2?1=3.
?
知识大全
考点二 解分式方程
分式方程的概念:分母中含有未知数的方程叫做分式方程.
增根的概念:在方程变形时,有时可能产生不适合原方程的根,这种根叫做方程的增根.
易错易混
考点二 解分式方程
1. 分式方程与整式方程的根本区别:分母中含有未知数,也是判断分式方程的依据.
2. 去分母时要把方程两边的式子作为一个整体,记得不要漏乘整式项.
3. 分式方程的结果还要代回方程的最简公分母中,只有最简公分母不是零的解才是原方程的解.
4. 分式方程的增根是去分母后的整式方程的根,也是使分式方程的公分母为0的根,它不是原分式方程的根.
5. 解分式方程可能产生使分式方程无意义的根,检验是解分式方程的必要步骤.
6. 分式方程有增根与无解并非是同一个概念.分式方程无解,需分类讨论:可能是解为增根,也可能是去分母后的整式方程无解.
热考题型
考点二 解分式方程
1.(23-24八年级上·山东聊城·阶段练习)下列关于x的方程中(1)1????=1;(2)2????+13=1+1?3????4;(3)????????+????????=1;(4)?????????3=????+4;(5)2????+3????????+1=0,其中是分式方程的有(????)
A.1个 B.2个 C.3个 D.4个
2.(23-24八年级下·江苏扬州·阶段练习)解方程:
(1)2?????5?????2+3=3?????3?????2;
(2)?????????2?1=8????2?4.
?
【详解】(1)解:2?????5?????2+3=3?????3?????2,
去分母得:2?????5+3?????2=3?????3,
去括号得:2?????5+3?????6=3?????3,
移项合并同类项得:2????=8,
系数化为1得:????=4,
检验:把????=4代入?????2得:?????2=4?2=2≠0,∴????=4是原方程的解.
?
(2)解:?????????2?1=8????2?4,
去分母得:????????+2?????2?4=8,
去括号得:????2+2?????????2+4=8,
移项合并同类项得:2????=4,
系数化为1得:????=2,
检验:把????=2代入????2?4得:????2?4=4?4=0,
∴????=2是原方程的增根,
∴原方程无解.
?
热考题型
考点二 解分式方程
3.(23-24八年级上·山东东营·期中)若关于x的方程3?????????=22?????1有解,则a的值不能为(????)
A.3 B.2 C.13 D.12
?
【详解】解:两边同时乘以(?????????)(2?????1)得,
6?????3=2?????2????,
解得:????=3?2????4,
∵方程3?????????=22?????1有解,
∴当????=3?2????4时(?????????)(2?????1)不等于0,
即:3?2????4?????≠0,2×3?2????4?1≠0,
解得:????≠12,
故选:D.
?
热考题型
考点二 解分式方程
4.(23-24八年级下·全国·课后作业)已知关于x的分式方程??????????????1?3????=1+????????2?????无解,求a的值.
?
【详解】
解:方程两边都乘?????????1,得??????????????3?????1=?????????1+????,
整理,得????+2????=3?????.①
当????+2=0,3?????≠0,
即????=?2时,方程①无解,则原方程无解;
当????+2≠0,即????≠?2时,
∵原分式方程无解,
∴?????????1=0,即????=0或????=1.
把????=0代入①,得????=3,
把????=1代入①,得????=12.
综上,a的值为?2或3或12.
?
热考题型
考点二 解分式方程
5.(23-24八年级下·上海浦东新·阶段练习)按照解分式方程的一般步骤解关于????的分式方程????(????+1)(?????1)+7=1?????1,出现增根????=1,那么????的值为 .
?
【详解】解:去分母得:????+7(????+1)(?????1)=????+1,
将增根????=1代入得:????+7×1+1×1?1=1+1,
解得:????=2,
?
热考题型
考点二 解分式方程
6.(23-24八年级下·河南南阳·阶段练习)若数a使关于x的分式方程2?????1+????1?????=4的解为非负数,则a的取值正确的是 .
?
【详解】解:分式方程整理得:2?????1??????????1=4,
去分母得:2?????=4?????4,解得????=6?????4,
由分式方程的解为非负数,得到6?????4≥0且6?????4≠1
解得????≤6且????≠2.
故答案为:????≤6且????≠2.
?
热考题型
考点二 解分式方程
7.(22-23八年级上·河北沧州·期中)已知方程????????????+1?2????+1=2的解与方程????????+1+2?????1=1的解相同,求a的值.
?
【详解】解:化为整式方程得:x(x﹣1)+2(x+1)=x2﹣1,
化简得:x=﹣3,
经检验x=﹣3是原方程的解,
∴原方程的解是x=﹣3,
将x=-3代入????????????+1?2????+1=2,
解得a=?14,
经检验a=?14是原方程的解,
∴a=?14.
?
知识大全
考点三 用分式方程解决实际问题
用分式方程解决实际问题的步骤:
审:理解并找出实际问题中的等量关系;
设:用代数式表示实际问题中的基础数据;
列:找到所列代数式中的等量关系,以此为依据列出方程;
解:求解方程;
验:考虑求出的解是否具有实际意义;+
1)检验所求的解是否是所列分式方程的解.
2)检验所求的解是否符合实际意义.
答:实际问题的答案.
解题大全
考点三 用分式方程解决实际问题
与分式方程有关应用题的常见类型:
热考题型
考点三 用分式方程解决实际问题
1.(23-24八年级下·福建福州·开学考试)为落实“全民健身国家战略,推动健康中国建设”,我市体育局组织了系列的体育赛事,其中半程马拉松(21.0975公里),他们约好一起去公园长跑训练,跑完后,发现小林用52分钟跑的路程和小李用57分钟跑的路程一样多,而小林的平均配速比小李的平均配速小0.5分钟/公里,问这次训练小林和小李的平均配速各是多少分钟/公里.(说明:“配速”是速度的一种,指每公里所花的时间,它是长跑者关注的一项重要指标)
?
【详解】解:设这次训练小林的平均配速为x分钟/公里,则这次训练小李的平均配速为(????+0.5)分钟/公里,由题意可得,
依题意得:52????=57????+0.5,
解得:????=5.2,
经检验,????=5.2是原方程的解,
∴5.2+0.5=5.7,
答:这次训练小林的平均配速为5.2分钟/公里,小李的平均配速为5.7分钟/公里.
?
热考题型
考点三 用分式方程解决实际问题
2.(23-24八年级上·河北邯郸·期末)甲、乙两个工程队共同参与一项筑路工程,甲队单独施工需90天完成.甲队先单独施工30天,然后增加了乙队,两队又合做了15天.总工程全部完成.求乙队单独施工需多少天完成.
【详解】解:设乙队单独施工需????天完成,
根据题意得:3090+1590+15????=1,
解得:????=30,
经检验,????=30是分式方程3090+1590+15????=1的解.
答:乙队单独施工需30天完成.
?
热考题型
考点三 用分式方程解决实际问题
3.(23-24八年级上·湖南岳阳·期中)某超市用6 000元购进一批“红富士”苹果进行试销,由于销售状况良好,超市又调拨13 000元资金购进该品种苹果,但这次的进价比试销时的进价每千克多了0.5元,购进苹果的质量是试销时的2倍.
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种苹果按每千克8元的定价出售,当大部分苹果售出后,余下的400千克按定价的7折(“7折”即定价的70%)售完,那么超市在这两次苹果销售中共盈利多少元?
?
【详解】(1)解:设试销时该品种苹果的进价是每千克????元,
依题意可得:13000????+0.5=6000????×2,解得????=6.
经检验,????=6是原方程的解,且符合题意.
答:试销时该品种苹果的进价是每千克6元.
(2)解:试销时购进苹果的质量为60006=1000(千克),
第二次购进苹果的质量为2×1000=2000(千克),
盈利为1000+2000?400×8+400×8×0.7?6000?13000=4040(元).
答:超市在这两次苹果销售中共盈利4040元.
?
热考题型
考点三 用分式方程解决实际问题
4.(23-24八年级上·吉林长春·期末)一艘轮船沿江顺流航行100千米和逆流航行60千米所有的时间相同.已知水流的速度是5千米/时,求轮船在静水中的速度.
【详解】解:设轮船在静水中的速度为x千米/时.
依题意得:100????+5=60?????5,
解得:????=20,
经检验:????=20是原方程的解,且符合题意.?????
答:轮船在静水中的速度为20千米/时.
?
谢谢!
串讲03 分式
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
考点一 分式的运算
分式的概念:如果A,B表示两个整式,并且B中含有字母,那么式子AB叫做分式,A为分子,B为分母.
对于分式AB来说: ①当B≠0时,分式有意义;当 B=0时,分式无意义.
②当A=0且B≠0这两个条件同时满足时,分式值为0.
③当A=B时,分式的值为1.当A+B=0时,分式的值为-1.
④若AB>0,则A、B同号; 若AB<0,则A、B异号.
约分的定义:把一个分式的分子与分母的公因式约去,叫分式的约分.
最简公式的定义:分子与分母没有公因式的分式,叫做最简分式.
通分的定义:把几个异分母的分式分别化成与原来的分式相等的同分母分式,这一过程叫做分式的通分.
通分步骤:①定最简公分母;②化异分母为最简公分母.
最简公分母的定义:通常取各分母系数的最小公倍数与所有字母因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
?
解题技巧
考点一 分式的基础
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类型
确定最简公分母的方法
?
分母为单项式
1)取单项式中所有系数的最小公倍数作为最简公分母的系数;
2)取单项式中每个字母出现的最高次数作为最简公分母中该字母的次数.
?
分母为多项式
1)对每个分母因式分解;
2)找出每个出现的因式的最高次幂,它们的积为最简公分母;
3) 若有系数,求各分母系数的最小公倍数作为最简公分母的系数.
知识大全
考点一 分式的基础
分式的基本性质:分式的分子和分母同乘(或除以)一个不等于0的整式,分式的值不变. 即:AB=A?CB?C(C≠0)或AB=A÷CB÷C(C≠0),其中A,B,C是整式.
分式符号法则:分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变,即:AB=?A?B=??AB=?A?B.
?
知识大全
考点一 分式的基础
热考题型
考点一 分式的基础
1.(23-24八年级下·河南南阳·阶段练习)在代数式?????????????,????2,2????+3,13????+????中,属于分式的有(???)
A.1个 B.2个 C.3个 D.4个
?
2.(23-24八年级下·全国·课后作业)若代数式?????2?????3有意义,则x的取值范围是( )
A.????>2且????≠3 B.????≥2
C.????≠3 D.????≥2且????≠3
?
3.(21-22八年级上·贵州铜仁·期末)下列关于分式的判断,正确的是(????)
A.当????=2时,????+1?????2的值为0
B.当????≠3时,?????3????有意义
C.无论x为何值,3????+1的值不可能是正整数
D.无论x为何值,1????2+1总有意义
?
【详解】解:A.当????=2时,分式????+1?????2无意义,故该选项错误,不符合题意;
B.当????=0时,分式?????3????无意义,故该选项错误,不符合题意;
C.当????=2时,分式3????+1=1,为正整数,故该选项错误,不符合题意;
D.因为无论x为何值????2+1≥1,即????2+1≠0,
所以分式1????2+1总有意义,故该选项正确,符合题意.
故选D.
?
热考题型
考点一 分式的基础
4.(23-24八年级上·山东临沂·期末)已知????2??????6=0,则2????????2+3?????6的值是(????)
A.13 B.12 C.23 D.1
5.(23-24八年级上·湖南长沙·阶段练习)若分式2????+1????2的值为正,则????的取值范围是(??? )
A.????>0 B.????>?12 C.????≠?12 D.????>?12且????≠0
?
【详解】解:∵????2??????6=0,∴????2?????=6,
∴2????????2+3?????6=2????????2?????+4?????6=2????6+4?????6=2????4????=12,故选:B.
?
【详解】解:由题意得,????2>0,且????≠0,
∵分式2????+1????2的值为正,∴2????+1>0,
∴????>?12,∴????>?12且????≠0.
故选:D.
?
热考题型
考点一 分式的基础
6.(23-24八年级上·全国·课后作业)(1)当????取什么值时,分式????+13?????2有意义?
(2)当????取什么值时,分式?15?????的值为负?
(3)当????取什么值时,分式?????21+????2的值为负?
(4)当????取什么值时,分式????2?1????+1的值为0?
?
【详解】解:(1)∵分式????+13?????2有意义∴3?????2≠0,解得:????≠23;
(2)∵分式?15?????的值为负∴5?????>0,∴????<5;
(3)∵分式?????21+????2的值为负∴1+????2>0且?????2<0,??∴????≠0;
(4)∵分式????2?1????+1的值为0,∴????2?1=0且????+1≠0,解得:????=1
?
热考题型
考点一 分式的基础
7.(23-24八年级上·黑龙江牡丹江·期末)观察下列关于????的分式,探究其规律:2????,5????3,8????5,11????7,?,按着上述规律,第????个分式是 .
?
【详解】解:根据分式的分子和分母的规律可得,第????个分式是3?????1????2?????1.
?
8.(23-24八年级下·江苏泰州·阶段练习)计算.
(1)约分:????2+4????????+4????2????2?4????2 ;
(2)通分:????????2?????????,?????????????2+????????.
?
【详解】(1)????2+4????????+4????2????2?4????2=????+2????2????+2?????????2????=????+2?????????2????;
(2)∵????????2?????????=?????????????????,?????????????2+????????=?????????????????+????
∴????????2?????????=?????????????????+????=??????+?????????????????????+????,
?????????????2+????????=?????????????????+????=??????????????????????????+?????????????=?????????2????????+?????????????,
?
热考题型
考点一 分式的基础
9.(21-22八年级下·陕西咸阳·阶段练习)下列各选项中,所求的最简公分母错误的是(????)
A.12????与13????的最简公分母是6????
B.12????2????与2????????3????的最简公分母是2????2????????
C.1????2?4与1????+2的最简公分母是????+2?????2
D.????3?????3????与?????????????的最简公分母是3?????????
?
【详解】解:12????与13????的最简公分母是6????,故A正确,不符合题意,
12????2????与2????????3????的最简公分母是2????2????3????,故B错误,符合题意,
1????2?4与1????+2的最简公分母是????+2?????2,故C正确,不符合题意,
????3?????3????与?????????????的最简公分母是3?????????,故D正确,不符合题意,
故选:B.
?
热考题型
考点一 分式的基础
10.(23-24八年级下·全国·课后作业)下列各式:①?????????????+????;②???????????????????;③???????????????????;④????????????????????.其中与?????????????+????相等的是( )
A.①②③ B.②③④ C.②③ D.③④
11.【热考易错】(23-24八年级下·江苏连云港·阶段练习)将分式?????3????????????中的m、n同时扩大为原来的3倍,分式的值将(????)
A.扩大3倍 B.不变 C.缩小为原来的13 D.缩小为原来的19
12.(23-24八年级上·全国·课堂例题)不改变分式的值,把分式12?????0.7????0.3????+????的分子与分母的各项系数化为整数为 .
?
【详解】解:12?????0.7????0.3????+????=0.5?????0.7????0.3????+????将分子、分母同时扩大10倍,不改变分式的值10×0.5?????0.7????10×0.3????+????=5?????7????3????+10????
?
热考题型
考点一 分式的基础
13.(22-23七年级上·上海黄浦·期中)已如3????2?7????+2?????1????+1=3+?????????1+????????+1是恒等式,请分别求的a、b的值.
?
【详解】解:3????2?7????+2?????1????+1=3+?????????1+????????+1,
∴去分母可得:3????2?7????+2=3????+1?????1+????????+1+?????????1,
∴3????2?7????+2=3????2+????+????????+??????????3,
由恒等式可得:????+????=?7??????????3=2,解得:????=?1????=?6.
?
热考题型
考点一 分式的基础
14.(23-24八年级下·江苏镇江·阶段练习)计算
(1)2????+3????+1?????+2????+1
(2)????2????2??????????????22????
(3)25?????2????2+10????+25÷????2?1????+5?????2+2????+1?????5
(4)?????3?????2÷????+2?5?????2
?
【详解】(1)解:原式=2????+3?????+2????+1=2????+3??????2????+1=????+1????+1=1;
(2)解:原式=?????2????2?????????????22????=?????????2????;
(3)解:原式=5?????5+????????+52÷?????1????+1????+5?????+12?????5=5?????5+????????+52?????+5?????1????+1?????+12?????5=?????+1?????1;
(4)解:原式=?????3?????2÷????2?4?????2?5?????2=?????3?????2÷????2?4?5?????2=?????3?????2÷????2?9?????2=?????3?????2÷?????3????+3?????2=?????3?????2??????2?????3????+3=1????+3.
?
热考题型
考点一 分式的基础
15.(23-24八年级下·河南南阳·阶段练习)先化简????2????+2?????+2÷4????????2?4,然后从?6?
【详解】解:????2????+2?????+2÷4????????2?4=????2?????2?2????+2????+4????+2÷4????????+2?????2=4????+2?????+2?????24????=?????2????,
∵分式要有意义,
∴????+2?????2≠0????≠0,
∴????≠±2且????≠0,
∵?6∴当????=1时,原式=1?21=?1;当????=?1时,原式=?1?2?1=3.
?
知识大全
考点二 解分式方程
分式方程的概念:分母中含有未知数的方程叫做分式方程.
增根的概念:在方程变形时,有时可能产生不适合原方程的根,这种根叫做方程的增根.
易错易混
考点二 解分式方程
1. 分式方程与整式方程的根本区别:分母中含有未知数,也是判断分式方程的依据.
2. 去分母时要把方程两边的式子作为一个整体,记得不要漏乘整式项.
3. 分式方程的结果还要代回方程的最简公分母中,只有最简公分母不是零的解才是原方程的解.
4. 分式方程的增根是去分母后的整式方程的根,也是使分式方程的公分母为0的根,它不是原分式方程的根.
5. 解分式方程可能产生使分式方程无意义的根,检验是解分式方程的必要步骤.
6. 分式方程有增根与无解并非是同一个概念.分式方程无解,需分类讨论:可能是解为增根,也可能是去分母后的整式方程无解.
热考题型
考点二 解分式方程
1.(23-24八年级上·山东聊城·阶段练习)下列关于x的方程中(1)1????=1;(2)2????+13=1+1?3????4;(3)????????+????????=1;(4)?????????3=????+4;(5)2????+3????????+1=0,其中是分式方程的有(????)
A.1个 B.2个 C.3个 D.4个
2.(23-24八年级下·江苏扬州·阶段练习)解方程:
(1)2?????5?????2+3=3?????3?????2;
(2)?????????2?1=8????2?4.
?
【详解】(1)解:2?????5?????2+3=3?????3?????2,
去分母得:2?????5+3?????2=3?????3,
去括号得:2?????5+3?????6=3?????3,
移项合并同类项得:2????=8,
系数化为1得:????=4,
检验:把????=4代入?????2得:?????2=4?2=2≠0,∴????=4是原方程的解.
?
(2)解:?????????2?1=8????2?4,
去分母得:????????+2?????2?4=8,
去括号得:????2+2?????????2+4=8,
移项合并同类项得:2????=4,
系数化为1得:????=2,
检验:把????=2代入????2?4得:????2?4=4?4=0,
∴????=2是原方程的增根,
∴原方程无解.
?
热考题型
考点二 解分式方程
3.(23-24八年级上·山东东营·期中)若关于x的方程3?????????=22?????1有解,则a的值不能为(????)
A.3 B.2 C.13 D.12
?
【详解】解:两边同时乘以(?????????)(2?????1)得,
6?????3=2?????2????,
解得:????=3?2????4,
∵方程3?????????=22?????1有解,
∴当????=3?2????4时(?????????)(2?????1)不等于0,
即:3?2????4?????≠0,2×3?2????4?1≠0,
解得:????≠12,
故选:D.
?
热考题型
考点二 解分式方程
4.(23-24八年级下·全国·课后作业)已知关于x的分式方程??????????????1?3????=1+????????2?????无解,求a的值.
?
【详解】
解:方程两边都乘?????????1,得??????????????3?????1=?????????1+????,
整理,得????+2????=3?????.①
当????+2=0,3?????≠0,
即????=?2时,方程①无解,则原方程无解;
当????+2≠0,即????≠?2时,
∵原分式方程无解,
∴?????????1=0,即????=0或????=1.
把????=0代入①,得????=3,
把????=1代入①,得????=12.
综上,a的值为?2或3或12.
?
热考题型
考点二 解分式方程
5.(23-24八年级下·上海浦东新·阶段练习)按照解分式方程的一般步骤解关于????的分式方程????(????+1)(?????1)+7=1?????1,出现增根????=1,那么????的值为 .
?
【详解】解:去分母得:????+7(????+1)(?????1)=????+1,
将增根????=1代入得:????+7×1+1×1?1=1+1,
解得:????=2,
?
热考题型
考点二 解分式方程
6.(23-24八年级下·河南南阳·阶段练习)若数a使关于x的分式方程2?????1+????1?????=4的解为非负数,则a的取值正确的是 .
?
【详解】解:分式方程整理得:2?????1??????????1=4,
去分母得:2?????=4?????4,解得????=6?????4,
由分式方程的解为非负数,得到6?????4≥0且6?????4≠1
解得????≤6且????≠2.
故答案为:????≤6且????≠2.
?
热考题型
考点二 解分式方程
7.(22-23八年级上·河北沧州·期中)已知方程????????????+1?2????+1=2的解与方程????????+1+2?????1=1的解相同,求a的值.
?
【详解】解:化为整式方程得:x(x﹣1)+2(x+1)=x2﹣1,
化简得:x=﹣3,
经检验x=﹣3是原方程的解,
∴原方程的解是x=﹣3,
将x=-3代入????????????+1?2????+1=2,
解得a=?14,
经检验a=?14是原方程的解,
∴a=?14.
?
知识大全
考点三 用分式方程解决实际问题
用分式方程解决实际问题的步骤:
审:理解并找出实际问题中的等量关系;
设:用代数式表示实际问题中的基础数据;
列:找到所列代数式中的等量关系,以此为依据列出方程;
解:求解方程;
验:考虑求出的解是否具有实际意义;+
1)检验所求的解是否是所列分式方程的解.
2)检验所求的解是否符合实际意义.
答:实际问题的答案.
解题大全
考点三 用分式方程解决实际问题
与分式方程有关应用题的常见类型:
热考题型
考点三 用分式方程解决实际问题
1.(23-24八年级下·福建福州·开学考试)为落实“全民健身国家战略,推动健康中国建设”,我市体育局组织了系列的体育赛事,其中半程马拉松(21.0975公里),他们约好一起去公园长跑训练,跑完后,发现小林用52分钟跑的路程和小李用57分钟跑的路程一样多,而小林的平均配速比小李的平均配速小0.5分钟/公里,问这次训练小林和小李的平均配速各是多少分钟/公里.(说明:“配速”是速度的一种,指每公里所花的时间,它是长跑者关注的一项重要指标)
?
【详解】解:设这次训练小林的平均配速为x分钟/公里,则这次训练小李的平均配速为(????+0.5)分钟/公里,由题意可得,
依题意得:52????=57????+0.5,
解得:????=5.2,
经检验,????=5.2是原方程的解,
∴5.2+0.5=5.7,
答:这次训练小林的平均配速为5.2分钟/公里,小李的平均配速为5.7分钟/公里.
?
热考题型
考点三 用分式方程解决实际问题
2.(23-24八年级上·河北邯郸·期末)甲、乙两个工程队共同参与一项筑路工程,甲队单独施工需90天完成.甲队先单独施工30天,然后增加了乙队,两队又合做了15天.总工程全部完成.求乙队单独施工需多少天完成.
【详解】解:设乙队单独施工需????天完成,
根据题意得:3090+1590+15????=1,
解得:????=30,
经检验,????=30是分式方程3090+1590+15????=1的解.
答:乙队单独施工需30天完成.
?
热考题型
考点三 用分式方程解决实际问题
3.(23-24八年级上·湖南岳阳·期中)某超市用6 000元购进一批“红富士”苹果进行试销,由于销售状况良好,超市又调拨13 000元资金购进该品种苹果,但这次的进价比试销时的进价每千克多了0.5元,购进苹果的质量是试销时的2倍.
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种苹果按每千克8元的定价出售,当大部分苹果售出后,余下的400千克按定价的7折(“7折”即定价的70%)售完,那么超市在这两次苹果销售中共盈利多少元?
?
【详解】(1)解:设试销时该品种苹果的进价是每千克????元,
依题意可得:13000????+0.5=6000????×2,解得????=6.
经检验,????=6是原方程的解,且符合题意.
答:试销时该品种苹果的进价是每千克6元.
(2)解:试销时购进苹果的质量为60006=1000(千克),
第二次购进苹果的质量为2×1000=2000(千克),
盈利为1000+2000?400×8+400×8×0.7?6000?13000=4040(元).
答:超市在这两次苹果销售中共盈利4040元.
?
热考题型
考点三 用分式方程解决实际问题
4.(23-24八年级上·吉林长春·期末)一艘轮船沿江顺流航行100千米和逆流航行60千米所有的时间相同.已知水流的速度是5千米/时,求轮船在静水中的速度.
【详解】解:设轮船在静水中的速度为x千米/时.
依题意得:100????+5=60?????5,
解得:????=20,
经检验:????=20是原方程的解,且符合题意.?????
答:轮船在静水中的速度为20千米/时.
?
谢谢!
同课章节目录
