专题02 中心对称图形-平行四边形【考点串讲】课件(共46张PPT) -八年级数学下学期期中考点大串讲(苏科版)
文档属性
| 名称 | 专题02 中心对称图形-平行四边形【考点串讲】课件(共46张PPT) -八年级数学下学期期中考点大串讲(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 20:58:18 | ||
图片预览









文档简介
(共46张PPT)
八年级苏科版数学下册期中考点大串讲
串讲02 中心对称图形-
平行四边形
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
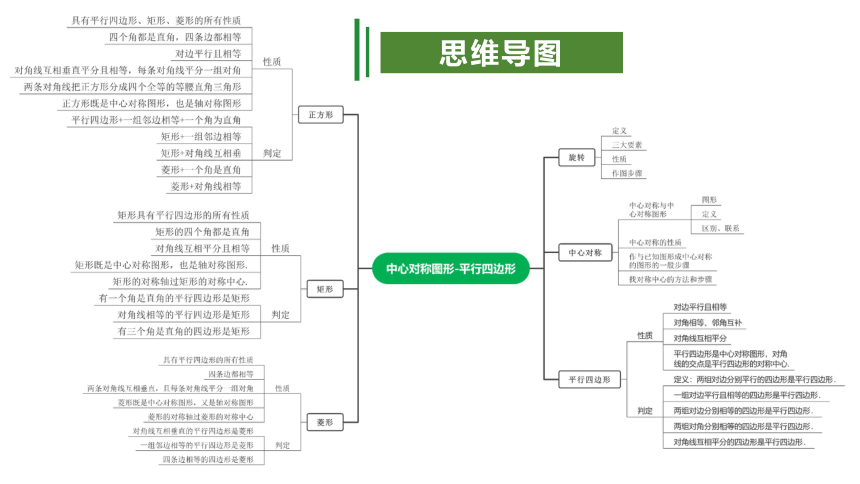
思维导图
知识大全
考点一 图形的旋转
旋转的定义:在平面内,一个图形绕一个定点沿某个方向(顺时针或逆时针)转过一个角度,这样的图形运动叫旋转.这个定点叫做旋转中心,转过的这个角叫做旋转角.
三大要素:旋转中心、旋转方向和旋转角度.
性质:
1)对应点到旋转中心的距离相等;
2)每对对应点与旋转中心所连线段的夹角等于旋转角;
3)旋转前后的图形全等.
作图步骤:
1)根据题意,确定旋转中心、旋转方向及旋转角;
2)找出原图形的关键点;
3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点;
4)按原图形依次连接对应点,得到旋转后的图形.
易错易混
考点一 图形的旋转
1. 图形的旋转由旋转中心、旋转方向与旋转的角度所决定.
2. 旋转中心可以是图形外的一点,也可以是图形上的一点,还可以是图形内的一点.
3. 对应点之间的运动轨迹是一段圆弧,对应点到旋转中心的线段就是这段圆弧所在圆的半径.
4. 旋转是一种全等变换,旋转改变的是图形的位置,图形的大小关系不发生改变,所以在解答有关旋转的问题时,要注意挖掘相等线段、角,因此特殊三角形性质的运用、锐角三角函数建立的边角关系起着关键的作用.
热考题型
考点一 图形的旋转
1.(22-23九年级上·广东韶关·期末)下列现象:①地下水位逐年下降,②传送带的移动,③方向盘的转动,④水龙头的转动;其中属于旋转的有( )
A.4个 B.3个 C.2个 D.1个
2.(22-23八年级上·山东济宁·期末)下列图形均可由“基本图案”通过变换得到:(只填序号)
既可以由“基本图案”平移,也可以通过旋转得到的有( )个.
A.1 B.2 C.3 D.4
3.(22-23八年级下·安徽宿州·期中)如图,是由旋转后得到的,下列说法正确的是( )
A.旋转中心不是点 B.
C.旋转方向是顺时针 D.
热考题型
考点一 图形的旋转
4.(22-23七年级上·河北邯郸·期末)如图,将绕点顺时针旋转一定的角度得到,此时点在边上,若,,则的长是 .
【详解】解:将绕点顺时针旋转一定的角度得到,
,,,
5.(23-24八年级上·山东东营·期末)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,的顶点均在格点上.
(1)画出关于原点O的中心对称图形;
(2)将绕点E顺时针旋转90°得到,画出;
(3)若由绕着某点旋转得到的,则这点的坐标为 .
(3)解:根据旋转的性质可得,旋转中心为和垂直平分线的交点,图中点P即为旋转中心,
∴,
热考题型
考点一 图形的旋转
6.(22-23八年级下·广东佛山·期中)有一种平面图形,它绕着中心旋转,不论旋转多少度,所得到的图形与原图形完全重合,你觉得它可能是( )
A.三角形 B.等边三角形 C.正方形 D.圆
7.(22-23八年级下·广东深圳·期中)如图,在平行四边形中,,,将平行四边形绕O点逆时针方向旋转得平行四边形,则点的坐标是( )
A. B. C. D.
【详解】解:∵将平行四边形绕O点逆时针方向旋转得平行四边形的位置,,
∴点的坐标是:.
热考题型
考点一 图形的旋转
8.(22-23八年级下·湖南怀化·期中)在平面直角坐标系中,点的坐标为,将点绕原点顺时针旋转度后得到点 ,则点坐标为 .
【详解】如图,过作轴于点,则,
∵,∴,
由题意得,,∴,
∴,
在中,由勾股定理得:,
∴点,
热考题型
考点一 图形的旋转
9.(23-24八年级上·山东泰安·期末)如图,在平面直角坐标系中,已知点、,对连续作旋转变换,依次得到三角形(1)、(2)、(3)、(4)、…,则第(2023)个三角形的直角顶点的坐标是 .
【详解】点,
,
第(3)个三角形的直角顶点的坐标是
即所求三角形的直角顶点是图形经过了每组为3个三角形的674组后的第一个三角形的直角顶点,而第674组的第三个三角形与下一组的第一个三角形的直角顶点重合,
第(2023)个三角形直角顶点的坐标是即.
故答案为:.
知识大全
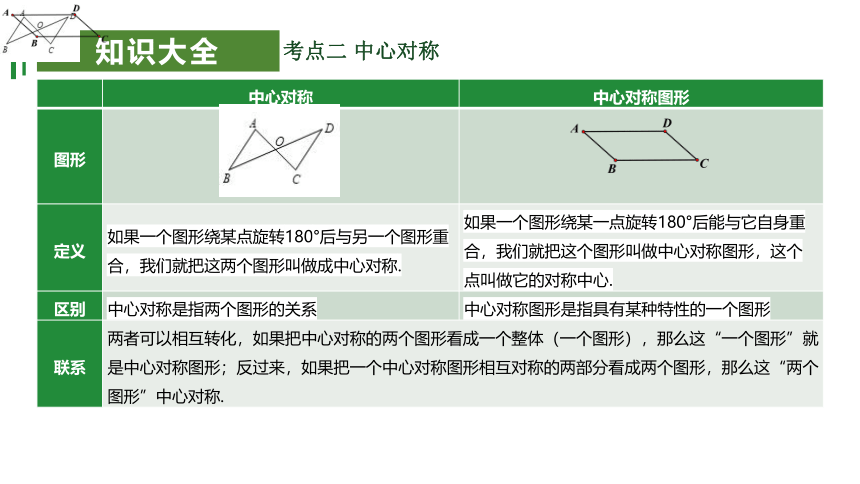
考点二 中心对称
中心对称 中心对称图形
图形
定义 如果一个图形绕某点旋转180°后与另一个图形重合,我们就把这两个图形叫做成中心对称. 如果一个图形绕某一点旋转180°后能与它自身重合,我们就把这个图形叫做中心对称图形,这个点叫做它的对称中心.
区别 中心对称是指两个图形的关系 中心对称图形是指具有某种特性的一个图形
联系 两者可以相互转化,如果把中心对称的两个图形看成一个整体(一个图形),那么这“一个图形”就是中心对称图形;反过来,如果把一个中心对称图形相互对称的两部分看成两个图形,那么这“两个图形”中心对称.
知识大全
考点二 中心对称
中心对称的性质:1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
中心对称的两个图形是全等图形.
作与已知图形成中心对称的图形的一般步骤:
1)作已知图形各顶点(或决定图形形状的关键点)关于对称中心的对称点——连接关键点和对称中心,并延长一倍确定关键点的对称点.
2)把各对称点按已知图形的连接方式依次连接起来,则所得到的图形就是已知图形关于对称中心对称的图形.
找对称中心的方法和步骤:
方法1:连接两个对应点,取对应点连线的中点,则中点为对称中心.
方法2:连接两个对应点,在连接两个对应点,两组对应点连线的交点为对称中心.
热考题型
考点二 中心对称
1.(2022·山西·模拟预测)中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
2.(23-24八年级上·河北张家口·期末)如图,线段与相交于点,且,则下列结论中正确的个数是( )
①;②;③线段与关于点成中心对称;④和关于点成中心对称.
A.4 B.3 C.2 D.1
热考题型
考点二 中心对称
3.(22-23八年级下·山东德州·期中)如图,在平行四边形中,,为对角线,,边上的高为5,则阴影部分的面积为( )
A.8 B.10 C.15 D.30
【详解】解:由图可知,图中阴影部分的每一块关于平行四边形的中心对称图形都在平行四边形上,且都是非阴影的部分,则阴影部分的面积为,故选:C.
4.(23-24八年级上·四川雅安·期末)已知,,则点关于原点对称的点的坐标是( )
A. B. C. D.
【详解】解:∵,∴,,
∴,,则点,
则点关于原点对称的点的坐标为
故选:C.
热考题型
考点二 中心对称
5.(23-24八年级上·山东淄博·期末)已知点和点关于坐标原点对称,则的值为( )
A. B. C.7 D.
【详解】解:∵点和点关于坐标原点对称,
∴,∴,
∴,故选:B.
6.(22-23八年级下·湖南常德·期中)如图所示,与关于点O中心对称,但点O不慎被涂掉了.
(1)请你找到对称中心O的位置.
(2)连接线段和线段,试判断四边形的形状,并说明理由.
(2)四边形是平行四边形
由中心对称的性质可得,,
∴四边形是平行四边形.
热考题型
考点二 中心对称
7.(22-23八年级下·浙江宁波·期中)如图,在的方格中,有4个小方格被涂黑成“L形”.
(1)在图1中再涂黑4格,使新涂黑的图形与原来的“L形“关于对称中心点O成中心对称;
(2)在图2和图3中再分别涂黑4格,使新涂黑的图形与原来的“L形”所组成的新图形既是轴对称图形又是中心对称图形(两个图各画一种).
知识大全
考点三 平行四边形
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形的表示:用符号“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
平行四边形的性质:
1)对边平行且相等;
2)对角相等、邻角互补;
3)对角线互相平分;
4)平行四边形是中心对称图形,但不是轴对称图形,平行四边形的对角线的交点是平行四边形的对称中心.
解题技巧
考点三 平行四边形
1)平行四边形相邻两边之和等于周长的一半.
2)平行四边形中有相等的边、角和平行关系,所以经常需结合三角形全等来解题.
3)过平行四边形对称中心的任一直线等分平行四边形的面积及周长.
4)如图①,AE平分∠BAD,则可利用平行线的性质结合等角对等边得到△ABE为等腰三角形,即AB=BE.
5)如图②,已知点E为AD上一点,根据平行线间的距离处处相等,可得S△BEC=S△ABE+S△CDE.
6)如图③,根据平行四边形的面积的求法,可得AE·BC=AF·CD.
知识大全
考点三 平行四边形
平行四边形的判定定理:
①定义:两组对边分别平行的四边形是平行四边形.
②一组对边平行且相等的四边形是平行四边形.
③两组对边分别相等的四边形是平行四边形.
④两组对角分别相等的四边形是平行四边形.
⑤对角线互相平分的四边形是平行四边形.
解题技巧
考点三 平行四边形
一般地,要判定一个四边形是平行四边形有多种方法,主要有以下三种思路:
1)当已知条件中有关于所证四边形的角时,可用“两组对角分别相等的四边形是平行四边形”来证明;
2)当已知条件中有关于所证四边形的边时,可选择“两组对边分别相等的四边形是平行四边形”或“两组对边分别平行的四边形是平行四边形”或“有一组对边平行且相等的四边形是平行四边形”来证明;
3)当已知条件中有关于所证四边形的对角线时,可选择“对角线互相平分的四边形是平行四边形”来证明.
热考题型
考点三 平行四边形
1.(22-23八年级下·天津河东·期中)如图,在平行四边形中,,,的平分线交于点E,则的长为 .
【详解】解:∵四边形是平行四边形,∴,∴,
∵的平分线交于点E,∴,∴,∴,
∵,,∴,
2.(23-24八年级上·山东泰安·期末)如图,E是平行四边形内任一点,若,则图中阴影部分的面积是( )
A.3 B.3.5 C.4 D.4.5
【详解】解:设两个阴影部分三角形的底为,高分别为,则为平行四边形的高,
∴.
故选:C.
热考题型
考点三 平行四边形
3.(2024八年级下·江苏·专题练习)不能判定四边形为平行四边形的题设是( )
A., B.平行且相等
C., D.,
4.(22-23八年级下·福建福州·期中)如图,E,F是对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
解:使四边形是平行四边形.就要使,,就要使,而在平行四边形中已有,,再加一个或可用证,或用证.
故答案为:或或.
热考题型
考点三 平行四边形
5.(23-24八年级上·山东威海·期末)如图,在边长为2的等边中,点为的延长线上的一点,连接,将绕点A逆时针旋转到,连接,过点作交直线于点.
(1)猜想线段之间的数量关系,并说明理由;
(2)求出的长度.
【详解】(1),理由:
∵是等边三角形,∴,
∵绕点A逆时针旋转到,∴,
∵,
∴,∴,∴,
∵,∴;
(2)∵,
∴,在等边中,,
∴,∴,
又∵,∴四边形是平行四边形.
∴,∴.
热考题型
考点三 平行四边形
6.(22-23八年级下·江苏无锡·阶段练习)如图,为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架,然后向右拉动框架,给出如下的判断:①四边形为平行四边形;②对角线的长度不变;③四边形的面积不变;④四边形的周长不变,其中所有正确的结论是 .
【详解】解:两组对边的长度分别相等,
四边形是平行四边形,故①正确,
向右扭动框架,
的长度变大,故②错误,
平行四边形的底不变,高变小了,
平行四边形的面积变小,故③错误,
平行四边形的四条边不变,
四边形的周长不变,故④正确.
故所有正确的结论是①④.
故答案为:①④
热考题型
考点三 平行四边形
7.(22-23八年级下·辽宁盘锦·期中)如图,中,AD平分,E是中点,,,,求的长.
【详解】解:延长交于点F,如图
AD平分,,
,
,
,
,
D是的中点,
E是中点,
.
知识大全
考点四 菱形
菱形的定义:有一组邻边相等的平行四边形叫做菱形.
菱形的性质:1)具有平行四边形的所有性质;
2)四条边都相等;
3)两条对角线互相垂直,且每条对角线平分一组对角.
4)菱形既是中心对称图形,又是轴对称图形,菱形的对称中心是菱形对角线的交点,菱形的对称轴是菱形对角线所在的直线,菱形的对称轴过菱形的对称中心.
菱形的判定:1)对角线互相垂直的平行四边形是菱形.
2)一组邻边相等的平行四边形是菱形.
3)四条边相等的四边形是菱形.
【解题思路】判定一个四边形是菱形时,可先说明它是平行四边形,再说明它的一组邻边相等或它的对角线互相垂直,也可直接说明它的四条边都相等或它的对角线互相垂直平分.
菱形的面积公式:S=ah=对角线乘积的一半(其中a为边长,h为高).
菱形的周长公式:周长l=4a(其中a为边长).
易错易混
考点四 菱形
1. 对于菱形的定义要注意两点:a.是平行四边形;b.一组邻边相等.
2. 定义说有一组邻边相等的平行四边形才是菱形,不要错误地理解为有一组邻边相等的四边形是菱形.
3. 菱形的面积S=对角线乘积的一半,适用于对角线互相垂直的任意四边形的面积的计算.
4. 在求菱形面积时,要根据图形特点及已知条体灵活选择面积公式来解决问题,
5. 在利用对角线长求菱形的面积时,要特别注意不要漏掉计算公式中的 .
热考题型
考点四 菱形
1.(23-24八年级上·吉林长春·期末)如图,在菱形中,,以点为圆心,以长为半径画弧,交对角线于点,再分别以点、为圆心,以大于的长为半径画弧,两弧相交于点,作射线交于点,则的大小为( )
A. B. C. D.
【详解】解:∵菱形,,
∴,,,
∴,
∴,
由作图可得:,,
∴,
∴;
故选C
热考题型
考点四 菱形
2.(22-23八年级下·云南迪庆·期末)如图,四边形是菱形,,,于点,则的长为( )
A. B. C. D.
【详解】
解:四边形是菱形,
,,,
,
,
,
故选:C
热考题型
考点四 菱形
3.(22-23八年级下·新疆吐鲁番·阶段练习)如图,菱形的两对角线,相交于点O,若,,则菱形的边长为 ,周长为 面积为
【详解】解:∵菱形的两对角线,相交于点O,,,
∴,,菱形的面积为,
∴,
∴
∴菱形的边长为,菱形的周长为,
故答案为:;;12.
热考题型
考点四 菱形
4.(23-24九年级上·河南周口·期末)如图,的对角线交于点O,下列条件不能判定是菱形的是( )
A. B.
C. D.
【详解】解:A.由、,根据邻边相等的平行四边形是菱形可得:四边形是菱形,故该选项不符合题意;
B.由可得,根据邻边相等的平行四边形是菱形可得:四边形是菱形,故该选项不符合题意;
C.由,根据对角线垂直的平行四边形是菱形可得:四边形是菱形,故该选项不符合题意;
C.是的对边,不能说明四边形是菱形,故该选项符合题意.
故选:D.
热考题型
考点四 菱形
5.(22-23八年级下·江苏泰州·阶段练习)如图,在四边形中,,点在的延长线上,,连接,交边于点,且.
(1)求证:;
(2)连接、,若,求证:四边形为菱形.
【详解】(1)证明:,,
在和中,,,,
,;
(2)证明:,,四边形是平行四边形,
,,
,,四边形是菱形.
知识大全
考点五 矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形.
矩形的性质:1)矩形具有平行四边形的所有性质;
2)矩形的四个角都是直角;
3)对角线互相平分且相等;
4)矩形既是中心对称图形,也是轴对称图形.矩形的对称中心是矩形对角线的交点;矩形有两条对称轴,矩形的对称轴是过矩形对边中点的直线;矩形的对称轴过矩形的对称中心.
【推论】1)在直角三角形中斜边的中线,等于斜边的一半.
2)直角三角形中,30度角所对应的直角边等于斜边的一半.
矩形的判定:1) 有一个角是直角的平行四边形是矩形;
2)对角线相等的平行四边形是矩形;
3)有三个角是直角的四边形是矩形.
【解题思路】要证明一个四边形是矩形,首先要判断四边形是否为平行四边形,若是,则需要再证明对角线相等或有一个角是直角;若不易判断,则可通过证明有三个角是直角来直接证明.
热考题型
考点五 矩形
1.(23-24九年级上·四川成都·阶段练习)如图,在矩形中,,,对角线,相交于点O.点,分别是,的中点,连接,则的周长为( )
A.12 B.18 C.20 D.16
【详解】在矩形中,,,
,
对角线,相交于点O,,点E,F分别是,的中点,
是的中位线,
,,
,
的周长为:,
故选:B.
热考题型
考点五 矩形
2.(22-23八年级下·浙江宁波·期中)如图,点是矩形内一点,连结,,,,,知道下列哪个选项的值就能要求的面积( )
A.与面积之差 B.与面积之差
C.与面积之差 D.与面积之差
【详解】解:过作于,延长交于,
四边形是矩形,,,,
的面积,的面积,
的面积的面积矩形的面积,
的面积矩形的面积,
的面积的面积的面积,
的面积的面积的面积的面积,
的面积的面积的面积的面积的面积的面积的面积.
故选:C.
热考题型
考点五 矩形
3.(23-24八年级上·山东临沂·期末)如图,在长方形中,,点在线段上,且,动点在线段上,从点出发以的速度向点运动,同时点在线段上,以的速度由点向点运动,当与全等时,的值为( )
A. B. C.或 D.或
【详解】解:当与全等时,有两种情况,
当,,,
∵,∴,∴,
∴点和点运动的时间为,,∴;
当,,,此时,,,
∴点和点运动的时间为为,∴;
∴的值为或,故选:.
热考题型
考点五 矩形
4.(22-23八年级下·河南商丘·期末)如图,在中,于点E,点在边的延长线上,则添加下列条件不能证明四边形是矩形的是( )
A. B.
C. D.
【详解】解:四边形是平行四边形,∴,,
,,
,,四边形是矩形,故A不符合题意;
,,
∵,,四边形是矩形,故B不符合题意;
,,即,,四边形是平行四边形,
又,,平行四边形是矩形,故C不符合题意;
,
,故四边形不能判定是矩形,故D符合题意;
故选:D.
热考题型
考点五 矩形
5.(22-23八年级下·浙江宁波·阶段练习)如图,在四边形中,,E,F,G,H分别是的中点,求证:四边形是矩形.
【详解】证明:如图所示,连接,
∵,
∴垂直平分,即,
∵E,F分别是的中点,
∴是的中位线,
∴,
同理得,,
∴,
∴四边形是平行四边形,
∴平行四边形是矩形.
热考题型
考点五 矩形
6.(22-23八年级下·浙江杭州·期中)如图所示,在四边形中,对角线,相交于点O,,,且,.
(1)求证:四边形是矩形.
(2)若,于点E,求的度数.
【详解】(1)证明:∵在四边形中,对角线,相交于点O,,,
∴四边形是平行四边形,,
∵,,∴,
∴,∴四边形是矩形;
(2)∵四边形是矩形∴,
∵,,∴,
∵,∴,
∵四边形是矩形,∴,
∴,∴.
知识大全
考点六 正方形
正方形的定义:四条边都相等,四个角都是直角的四边形叫做正方形.
正方形的性质:
1)正方形具有平行四边形、矩形、菱形的所有性质.
2)正方形的四个角都是直角,四条边都相等.
3)正方形对边平行且相等.
4)正方形的对角线互相垂直平分且相等,每条对角线平分一组对角;
5)正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
6)正方形既是中心对称图形,也是轴对称图形.
【补充】正方形对角线与边的夹角为45°.
正方形的判定:1)平行四边形+一组邻边相等+一个角为直角;
2)矩形+一组邻边相等;
3)矩形+对角线互相垂直;
4)菱形+一个角是直角;
5)菱形+对角线相等.
知识大全
考点六 正方形
正方形的面积公式:面积==对角线乘积的一半=2S△ABC=4S△AOB.
正方形的周长公式:周长= 4a
解题大全
考点六 正方形
判定一个四边形是正方形通常先证明它是矩形,再证明它有一组邻边相等或对角线互相垂直;或者先证明它是菱形,再证明它有一个角是直角或对角线相等;还可以先判定四边形是平行四边形,再证明它有一个角为直角和一组邻边相等.
热考题型
考点六 正方形
1.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
【详解】观察图形可知, 所在的三角形与3所在的三角形全等,
,又,.故选D.
热考题型
考点六 正方形
2.如图,已知在正方形ABCD中,E是BC上一点,将正方形的边CD沿DE折叠到DF,延长EF交AB于点G,连接DG.现有如下4个结论:①AG=GF;②AG与EC一定不相等;③;④的周长是一个定值.其中正确的个数为( )
A.1 B.2 C.3 D.4
【详解】根据折叠的意义,得△DEC≌△DEF,
∴EF=EC,DF=DC,∠CDE=∠FDE,
∵DA=DF,DG=DG,∴Rt△ADG≌Rt△FDG,
∴AG=FG,∠ADG=∠FDG,∴∠GDE=∠FDG+∠FDE=(∠ADF+∠CDF)=45°,
∵△BGE的周长=BG+BE+GE,GE=GF+EF=EC+AG,
∴△BGE的周长=BG+BE+ EC+AG=AB+AC,是定值,
∴正确的结论有①③④,故选C.
热考题型
考点六 正方形
3.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
【详解】设CH=x, 因为BE:EC=2:1,BC=9,所以,EC=3,
由折叠知,EH=DH=9-x,
在Rt△ECH中,由勾股定理,得:,解得:x=4,即CH=4
4.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
谢谢!
八年级苏科版数学下册期中考点大串讲
串讲02 中心对称图形-
平行四边形
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
考点一 图形的旋转
旋转的定义:在平面内,一个图形绕一个定点沿某个方向(顺时针或逆时针)转过一个角度,这样的图形运动叫旋转.这个定点叫做旋转中心,转过的这个角叫做旋转角.
三大要素:旋转中心、旋转方向和旋转角度.
性质:
1)对应点到旋转中心的距离相等;
2)每对对应点与旋转中心所连线段的夹角等于旋转角;
3)旋转前后的图形全等.
作图步骤:
1)根据题意,确定旋转中心、旋转方向及旋转角;
2)找出原图形的关键点;
3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点;
4)按原图形依次连接对应点,得到旋转后的图形.
易错易混
考点一 图形的旋转
1. 图形的旋转由旋转中心、旋转方向与旋转的角度所决定.
2. 旋转中心可以是图形外的一点,也可以是图形上的一点,还可以是图形内的一点.
3. 对应点之间的运动轨迹是一段圆弧,对应点到旋转中心的线段就是这段圆弧所在圆的半径.
4. 旋转是一种全等变换,旋转改变的是图形的位置,图形的大小关系不发生改变,所以在解答有关旋转的问题时,要注意挖掘相等线段、角,因此特殊三角形性质的运用、锐角三角函数建立的边角关系起着关键的作用.
热考题型
考点一 图形的旋转
1.(22-23九年级上·广东韶关·期末)下列现象:①地下水位逐年下降,②传送带的移动,③方向盘的转动,④水龙头的转动;其中属于旋转的有( )
A.4个 B.3个 C.2个 D.1个
2.(22-23八年级上·山东济宁·期末)下列图形均可由“基本图案”通过变换得到:(只填序号)
既可以由“基本图案”平移,也可以通过旋转得到的有( )个.
A.1 B.2 C.3 D.4
3.(22-23八年级下·安徽宿州·期中)如图,是由旋转后得到的,下列说法正确的是( )
A.旋转中心不是点 B.
C.旋转方向是顺时针 D.
热考题型
考点一 图形的旋转
4.(22-23七年级上·河北邯郸·期末)如图,将绕点顺时针旋转一定的角度得到,此时点在边上,若,,则的长是 .
【详解】解:将绕点顺时针旋转一定的角度得到,
,,,
5.(23-24八年级上·山东东营·期末)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,的顶点均在格点上.
(1)画出关于原点O的中心对称图形;
(2)将绕点E顺时针旋转90°得到,画出;
(3)若由绕着某点旋转得到的,则这点的坐标为 .
(3)解:根据旋转的性质可得,旋转中心为和垂直平分线的交点,图中点P即为旋转中心,
∴,
热考题型
考点一 图形的旋转
6.(22-23八年级下·广东佛山·期中)有一种平面图形,它绕着中心旋转,不论旋转多少度,所得到的图形与原图形完全重合,你觉得它可能是( )
A.三角形 B.等边三角形 C.正方形 D.圆
7.(22-23八年级下·广东深圳·期中)如图,在平行四边形中,,,将平行四边形绕O点逆时针方向旋转得平行四边形,则点的坐标是( )
A. B. C. D.
【详解】解:∵将平行四边形绕O点逆时针方向旋转得平行四边形的位置,,
∴点的坐标是:.
热考题型
考点一 图形的旋转
8.(22-23八年级下·湖南怀化·期中)在平面直角坐标系中,点的坐标为,将点绕原点顺时针旋转度后得到点 ,则点坐标为 .
【详解】如图,过作轴于点,则,
∵,∴,
由题意得,,∴,
∴,
在中,由勾股定理得:,
∴点,
热考题型
考点一 图形的旋转
9.(23-24八年级上·山东泰安·期末)如图,在平面直角坐标系中,已知点、,对连续作旋转变换,依次得到三角形(1)、(2)、(3)、(4)、…,则第(2023)个三角形的直角顶点的坐标是 .
【详解】点,
,
第(3)个三角形的直角顶点的坐标是
即所求三角形的直角顶点是图形经过了每组为3个三角形的674组后的第一个三角形的直角顶点,而第674组的第三个三角形与下一组的第一个三角形的直角顶点重合,
第(2023)个三角形直角顶点的坐标是即.
故答案为:.
知识大全
考点二 中心对称
中心对称 中心对称图形
图形
定义 如果一个图形绕某点旋转180°后与另一个图形重合,我们就把这两个图形叫做成中心对称. 如果一个图形绕某一点旋转180°后能与它自身重合,我们就把这个图形叫做中心对称图形,这个点叫做它的对称中心.
区别 中心对称是指两个图形的关系 中心对称图形是指具有某种特性的一个图形
联系 两者可以相互转化,如果把中心对称的两个图形看成一个整体(一个图形),那么这“一个图形”就是中心对称图形;反过来,如果把一个中心对称图形相互对称的两部分看成两个图形,那么这“两个图形”中心对称.
知识大全
考点二 中心对称
中心对称的性质:1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
中心对称的两个图形是全等图形.
作与已知图形成中心对称的图形的一般步骤:
1)作已知图形各顶点(或决定图形形状的关键点)关于对称中心的对称点——连接关键点和对称中心,并延长一倍确定关键点的对称点.
2)把各对称点按已知图形的连接方式依次连接起来,则所得到的图形就是已知图形关于对称中心对称的图形.
找对称中心的方法和步骤:
方法1:连接两个对应点,取对应点连线的中点,则中点为对称中心.
方法2:连接两个对应点,在连接两个对应点,两组对应点连线的交点为对称中心.
热考题型
考点二 中心对称
1.(2022·山西·模拟预测)中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
2.(23-24八年级上·河北张家口·期末)如图,线段与相交于点,且,则下列结论中正确的个数是( )
①;②;③线段与关于点成中心对称;④和关于点成中心对称.
A.4 B.3 C.2 D.1
热考题型
考点二 中心对称
3.(22-23八年级下·山东德州·期中)如图,在平行四边形中,,为对角线,,边上的高为5,则阴影部分的面积为( )
A.8 B.10 C.15 D.30
【详解】解:由图可知,图中阴影部分的每一块关于平行四边形的中心对称图形都在平行四边形上,且都是非阴影的部分,则阴影部分的面积为,故选:C.
4.(23-24八年级上·四川雅安·期末)已知,,则点关于原点对称的点的坐标是( )
A. B. C. D.
【详解】解:∵,∴,,
∴,,则点,
则点关于原点对称的点的坐标为
故选:C.
热考题型
考点二 中心对称
5.(23-24八年级上·山东淄博·期末)已知点和点关于坐标原点对称,则的值为( )
A. B. C.7 D.
【详解】解:∵点和点关于坐标原点对称,
∴,∴,
∴,故选:B.
6.(22-23八年级下·湖南常德·期中)如图所示,与关于点O中心对称,但点O不慎被涂掉了.
(1)请你找到对称中心O的位置.
(2)连接线段和线段,试判断四边形的形状,并说明理由.
(2)四边形是平行四边形
由中心对称的性质可得,,
∴四边形是平行四边形.
热考题型
考点二 中心对称
7.(22-23八年级下·浙江宁波·期中)如图,在的方格中,有4个小方格被涂黑成“L形”.
(1)在图1中再涂黑4格,使新涂黑的图形与原来的“L形“关于对称中心点O成中心对称;
(2)在图2和图3中再分别涂黑4格,使新涂黑的图形与原来的“L形”所组成的新图形既是轴对称图形又是中心对称图形(两个图各画一种).
知识大全
考点三 平行四边形
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形的表示:用符号“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
平行四边形的性质:
1)对边平行且相等;
2)对角相等、邻角互补;
3)对角线互相平分;
4)平行四边形是中心对称图形,但不是轴对称图形,平行四边形的对角线的交点是平行四边形的对称中心.
解题技巧
考点三 平行四边形
1)平行四边形相邻两边之和等于周长的一半.
2)平行四边形中有相等的边、角和平行关系,所以经常需结合三角形全等来解题.
3)过平行四边形对称中心的任一直线等分平行四边形的面积及周长.
4)如图①,AE平分∠BAD,则可利用平行线的性质结合等角对等边得到△ABE为等腰三角形,即AB=BE.
5)如图②,已知点E为AD上一点,根据平行线间的距离处处相等,可得S△BEC=S△ABE+S△CDE.
6)如图③,根据平行四边形的面积的求法,可得AE·BC=AF·CD.
知识大全
考点三 平行四边形
平行四边形的判定定理:
①定义:两组对边分别平行的四边形是平行四边形.
②一组对边平行且相等的四边形是平行四边形.
③两组对边分别相等的四边形是平行四边形.
④两组对角分别相等的四边形是平行四边形.
⑤对角线互相平分的四边形是平行四边形.
解题技巧
考点三 平行四边形
一般地,要判定一个四边形是平行四边形有多种方法,主要有以下三种思路:
1)当已知条件中有关于所证四边形的角时,可用“两组对角分别相等的四边形是平行四边形”来证明;
2)当已知条件中有关于所证四边形的边时,可选择“两组对边分别相等的四边形是平行四边形”或“两组对边分别平行的四边形是平行四边形”或“有一组对边平行且相等的四边形是平行四边形”来证明;
3)当已知条件中有关于所证四边形的对角线时,可选择“对角线互相平分的四边形是平行四边形”来证明.
热考题型
考点三 平行四边形
1.(22-23八年级下·天津河东·期中)如图,在平行四边形中,,,的平分线交于点E,则的长为 .
【详解】解:∵四边形是平行四边形,∴,∴,
∵的平分线交于点E,∴,∴,∴,
∵,,∴,
2.(23-24八年级上·山东泰安·期末)如图,E是平行四边形内任一点,若,则图中阴影部分的面积是( )
A.3 B.3.5 C.4 D.4.5
【详解】解:设两个阴影部分三角形的底为,高分别为,则为平行四边形的高,
∴.
故选:C.
热考题型
考点三 平行四边形
3.(2024八年级下·江苏·专题练习)不能判定四边形为平行四边形的题设是( )
A., B.平行且相等
C., D.,
4.(22-23八年级下·福建福州·期中)如图,E,F是对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
解:使四边形是平行四边形.就要使,,就要使,而在平行四边形中已有,,再加一个或可用证,或用证.
故答案为:或或.
热考题型
考点三 平行四边形
5.(23-24八年级上·山东威海·期末)如图,在边长为2的等边中,点为的延长线上的一点,连接,将绕点A逆时针旋转到,连接,过点作交直线于点.
(1)猜想线段之间的数量关系,并说明理由;
(2)求出的长度.
【详解】(1),理由:
∵是等边三角形,∴,
∵绕点A逆时针旋转到,∴,
∵,
∴,∴,∴,
∵,∴;
(2)∵,
∴,在等边中,,
∴,∴,
又∵,∴四边形是平行四边形.
∴,∴.
热考题型
考点三 平行四边形
6.(22-23八年级下·江苏无锡·阶段练习)如图,为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架,然后向右拉动框架,给出如下的判断:①四边形为平行四边形;②对角线的长度不变;③四边形的面积不变;④四边形的周长不变,其中所有正确的结论是 .
【详解】解:两组对边的长度分别相等,
四边形是平行四边形,故①正确,
向右扭动框架,
的长度变大,故②错误,
平行四边形的底不变,高变小了,
平行四边形的面积变小,故③错误,
平行四边形的四条边不变,
四边形的周长不变,故④正确.
故所有正确的结论是①④.
故答案为:①④
热考题型
考点三 平行四边形
7.(22-23八年级下·辽宁盘锦·期中)如图,中,AD平分,E是中点,,,,求的长.
【详解】解:延长交于点F,如图
AD平分,,
,
,
,
,
D是的中点,
E是中点,
.
知识大全
考点四 菱形
菱形的定义:有一组邻边相等的平行四边形叫做菱形.
菱形的性质:1)具有平行四边形的所有性质;
2)四条边都相等;
3)两条对角线互相垂直,且每条对角线平分一组对角.
4)菱形既是中心对称图形,又是轴对称图形,菱形的对称中心是菱形对角线的交点,菱形的对称轴是菱形对角线所在的直线,菱形的对称轴过菱形的对称中心.
菱形的判定:1)对角线互相垂直的平行四边形是菱形.
2)一组邻边相等的平行四边形是菱形.
3)四条边相等的四边形是菱形.
【解题思路】判定一个四边形是菱形时,可先说明它是平行四边形,再说明它的一组邻边相等或它的对角线互相垂直,也可直接说明它的四条边都相等或它的对角线互相垂直平分.
菱形的面积公式:S=ah=对角线乘积的一半(其中a为边长,h为高).
菱形的周长公式:周长l=4a(其中a为边长).
易错易混
考点四 菱形
1. 对于菱形的定义要注意两点:a.是平行四边形;b.一组邻边相等.
2. 定义说有一组邻边相等的平行四边形才是菱形,不要错误地理解为有一组邻边相等的四边形是菱形.
3. 菱形的面积S=对角线乘积的一半,适用于对角线互相垂直的任意四边形的面积的计算.
4. 在求菱形面积时,要根据图形特点及已知条体灵活选择面积公式来解决问题,
5. 在利用对角线长求菱形的面积时,要特别注意不要漏掉计算公式中的 .
热考题型
考点四 菱形
1.(23-24八年级上·吉林长春·期末)如图,在菱形中,,以点为圆心,以长为半径画弧,交对角线于点,再分别以点、为圆心,以大于的长为半径画弧,两弧相交于点,作射线交于点,则的大小为( )
A. B. C. D.
【详解】解:∵菱形,,
∴,,,
∴,
∴,
由作图可得:,,
∴,
∴;
故选C
热考题型
考点四 菱形
2.(22-23八年级下·云南迪庆·期末)如图,四边形是菱形,,,于点,则的长为( )
A. B. C. D.
【详解】
解:四边形是菱形,
,,,
,
,
,
故选:C
热考题型
考点四 菱形
3.(22-23八年级下·新疆吐鲁番·阶段练习)如图,菱形的两对角线,相交于点O,若,,则菱形的边长为 ,周长为 面积为
【详解】解:∵菱形的两对角线,相交于点O,,,
∴,,菱形的面积为,
∴,
∴
∴菱形的边长为,菱形的周长为,
故答案为:;;12.
热考题型
考点四 菱形
4.(23-24九年级上·河南周口·期末)如图,的对角线交于点O,下列条件不能判定是菱形的是( )
A. B.
C. D.
【详解】解:A.由、,根据邻边相等的平行四边形是菱形可得:四边形是菱形,故该选项不符合题意;
B.由可得,根据邻边相等的平行四边形是菱形可得:四边形是菱形,故该选项不符合题意;
C.由,根据对角线垂直的平行四边形是菱形可得:四边形是菱形,故该选项不符合题意;
C.是的对边,不能说明四边形是菱形,故该选项符合题意.
故选:D.
热考题型
考点四 菱形
5.(22-23八年级下·江苏泰州·阶段练习)如图,在四边形中,,点在的延长线上,,连接,交边于点,且.
(1)求证:;
(2)连接、,若,求证:四边形为菱形.
【详解】(1)证明:,,
在和中,,,,
,;
(2)证明:,,四边形是平行四边形,
,,
,,四边形是菱形.
知识大全
考点五 矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形.
矩形的性质:1)矩形具有平行四边形的所有性质;
2)矩形的四个角都是直角;
3)对角线互相平分且相等;
4)矩形既是中心对称图形,也是轴对称图形.矩形的对称中心是矩形对角线的交点;矩形有两条对称轴,矩形的对称轴是过矩形对边中点的直线;矩形的对称轴过矩形的对称中心.
【推论】1)在直角三角形中斜边的中线,等于斜边的一半.
2)直角三角形中,30度角所对应的直角边等于斜边的一半.
矩形的判定:1) 有一个角是直角的平行四边形是矩形;
2)对角线相等的平行四边形是矩形;
3)有三个角是直角的四边形是矩形.
【解题思路】要证明一个四边形是矩形,首先要判断四边形是否为平行四边形,若是,则需要再证明对角线相等或有一个角是直角;若不易判断,则可通过证明有三个角是直角来直接证明.
热考题型
考点五 矩形
1.(23-24九年级上·四川成都·阶段练习)如图,在矩形中,,,对角线,相交于点O.点,分别是,的中点,连接,则的周长为( )
A.12 B.18 C.20 D.16
【详解】在矩形中,,,
,
对角线,相交于点O,,点E,F分别是,的中点,
是的中位线,
,,
,
的周长为:,
故选:B.
热考题型
考点五 矩形
2.(22-23八年级下·浙江宁波·期中)如图,点是矩形内一点,连结,,,,,知道下列哪个选项的值就能要求的面积( )
A.与面积之差 B.与面积之差
C.与面积之差 D.与面积之差
【详解】解:过作于,延长交于,
四边形是矩形,,,,
的面积,的面积,
的面积的面积矩形的面积,
的面积矩形的面积,
的面积的面积的面积,
的面积的面积的面积的面积,
的面积的面积的面积的面积的面积的面积的面积.
故选:C.
热考题型
考点五 矩形
3.(23-24八年级上·山东临沂·期末)如图,在长方形中,,点在线段上,且,动点在线段上,从点出发以的速度向点运动,同时点在线段上,以的速度由点向点运动,当与全等时,的值为( )
A. B. C.或 D.或
【详解】解:当与全等时,有两种情况,
当,,,
∵,∴,∴,
∴点和点运动的时间为,,∴;
当,,,此时,,,
∴点和点运动的时间为为,∴;
∴的值为或,故选:.
热考题型
考点五 矩形
4.(22-23八年级下·河南商丘·期末)如图,在中,于点E,点在边的延长线上,则添加下列条件不能证明四边形是矩形的是( )
A. B.
C. D.
【详解】解:四边形是平行四边形,∴,,
,,
,,四边形是矩形,故A不符合题意;
,,
∵,,四边形是矩形,故B不符合题意;
,,即,,四边形是平行四边形,
又,,平行四边形是矩形,故C不符合题意;
,
,故四边形不能判定是矩形,故D符合题意;
故选:D.
热考题型
考点五 矩形
5.(22-23八年级下·浙江宁波·阶段练习)如图,在四边形中,,E,F,G,H分别是的中点,求证:四边形是矩形.
【详解】证明:如图所示,连接,
∵,
∴垂直平分,即,
∵E,F分别是的中点,
∴是的中位线,
∴,
同理得,,
∴,
∴四边形是平行四边形,
∴平行四边形是矩形.
热考题型
考点五 矩形
6.(22-23八年级下·浙江杭州·期中)如图所示,在四边形中,对角线,相交于点O,,,且,.
(1)求证:四边形是矩形.
(2)若,于点E,求的度数.
【详解】(1)证明:∵在四边形中,对角线,相交于点O,,,
∴四边形是平行四边形,,
∵,,∴,
∴,∴四边形是矩形;
(2)∵四边形是矩形∴,
∵,,∴,
∵,∴,
∵四边形是矩形,∴,
∴,∴.
知识大全
考点六 正方形
正方形的定义:四条边都相等,四个角都是直角的四边形叫做正方形.
正方形的性质:
1)正方形具有平行四边形、矩形、菱形的所有性质.
2)正方形的四个角都是直角,四条边都相等.
3)正方形对边平行且相等.
4)正方形的对角线互相垂直平分且相等,每条对角线平分一组对角;
5)正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
6)正方形既是中心对称图形,也是轴对称图形.
【补充】正方形对角线与边的夹角为45°.
正方形的判定:1)平行四边形+一组邻边相等+一个角为直角;
2)矩形+一组邻边相等;
3)矩形+对角线互相垂直;
4)菱形+一个角是直角;
5)菱形+对角线相等.
知识大全
考点六 正方形
正方形的面积公式:面积==对角线乘积的一半=2S△ABC=4S△AOB.
正方形的周长公式:周长= 4a
解题大全
考点六 正方形
判定一个四边形是正方形通常先证明它是矩形,再证明它有一组邻边相等或对角线互相垂直;或者先证明它是菱形,再证明它有一个角是直角或对角线相等;还可以先判定四边形是平行四边形,再证明它有一个角为直角和一组邻边相等.
热考题型
考点六 正方形
1.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
【详解】观察图形可知, 所在的三角形与3所在的三角形全等,
,又,.故选D.
热考题型
考点六 正方形
2.如图,已知在正方形ABCD中,E是BC上一点,将正方形的边CD沿DE折叠到DF,延长EF交AB于点G,连接DG.现有如下4个结论:①AG=GF;②AG与EC一定不相等;③;④的周长是一个定值.其中正确的个数为( )
A.1 B.2 C.3 D.4
【详解】根据折叠的意义,得△DEC≌△DEF,
∴EF=EC,DF=DC,∠CDE=∠FDE,
∵DA=DF,DG=DG,∴Rt△ADG≌Rt△FDG,
∴AG=FG,∠ADG=∠FDG,∴∠GDE=∠FDG+∠FDE=(∠ADF+∠CDF)=45°,
∵△BGE的周长=BG+BE+GE,GE=GF+EF=EC+AG,
∴△BGE的周长=BG+BE+ EC+AG=AB+AC,是定值,
∴正确的结论有①③④,故选C.
热考题型
考点六 正方形
3.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
【详解】设CH=x, 因为BE:EC=2:1,BC=9,所以,EC=3,
由折叠知,EH=DH=9-x,
在Rt△ECH中,由勾股定理,得:,解得:x=4,即CH=4
4.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
谢谢!
同课章节目录
