专题03 整式的乘法与因式分解【考点串讲】课件(共32张PPT)-七年级数学下学期期中考点大串讲(苏科版)
文档属性
| 名称 | 专题03 整式的乘法与因式分解【考点串讲】课件(共32张PPT)-七年级数学下学期期中考点大串讲(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 20:53:31 | ||
图片预览










文档简介
七年级苏科版数学下册期中考点大串讲
串讲03 整式的乘除与
因式分解
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
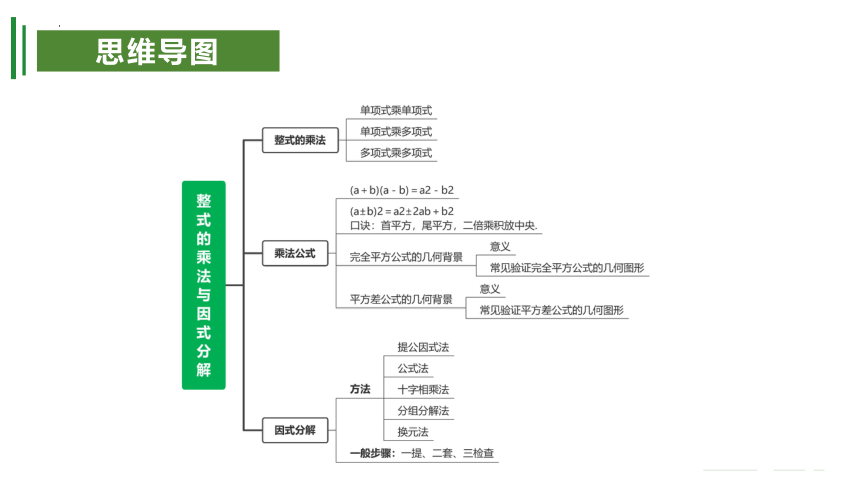
考点一 整式的乘法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}整式的乘法
运算步骤说明
补充说明及注意事项
单项式乘单项式
①将单项式系数相乘作为积的系数;
②相同字母的因式,利用同底数幂的乘法,作为积的一个因式;
③单独出现的字母,连同它的指数,作为积的一个因式.
1)实质:乘法的交换律和同底数幂的乘法法则的综合应用.
2)单项式乘单项式所得结果仍是单项式 .
单项式乘多项式
①先用单项式和多项式的每一项分别相乘;
②再把所得的积相加.
1)单项式乘多项式实质上是转化为单项式乘以单项式
2)单项式乘多项式的结果是多项式,积的项数与原多项式的项数相同.
多项式乘多项式
①先用一个多项式的每一项与另一个多项式的每一项相乘,
②再把所得的积相加.
运用法则时应注意以下两点:
①相乘时,按一定的顺序进行,必须做到不重不漏;
②多项式与多项式相乘,多项式的每一项都应该带上它前面的正负号.且结果仍是多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.
热考题型
考点一 整式的乘法
1.(23-24八年级上·河南南阳·阶段练习)计算下列各题
(1)34??????????????2????????????3
(2)????+1?????6?1?????4?????
?
【详解】(1)34??????????????2????????????3
=34???????????????8????3????3????3
=?6????4????4????3+8????3????4????3;
(2)????+1?????6?1?????4?????
=????2?6????+?????6?4??????4????+????2
=????2?6????+?????6?4+????+4?????????2
=?10.
?
热考题型
考点一 整式的乘法
2.(23-24八年级上·重庆渝中·期中)若????????2?????+3?????2????=????3+5?????6对任意????都成立,则????+????= .
?
【详解】
解:????????2?????+3?????2????=????3+5?????6,
????3?????????+3?????2????=????3+5?????6,
????3+?????+3?????2????=????3+5?????6,
∵原式子对任意????都成立,
∴?????+3=5,?2????=?6,
解得:????=?2,????=3,
∴????+????=?2+3=1.
故答案为:1.
?
热考题型
考点一 整式的乘法
3.(23-24八年级上·河南周口·阶段练习)在计算2????+????????+????时,甲错把b看成了6,得到的结果是:2????2+8?????24;乙错把a看成了?????,得到的结果是:2????2+14????+20,求a、b的值.
?
【详解】解:因为甲错把b看成了6,
则2????+????????+6=2????2+12+????????+6????=2????2+8?????24,
可得:????=?4,
因为乙错把a看成了?????,
则:2?????????????+????=2????+4????+????=2????2+2????+4????+4????=2????2+14????+20,
得:????=5.
?
热考题型
考点一 整式的乘法
4.(22-23七年级下·全国·假期作业)小红准备完成题目:计算 ,她发现第一个因式的一次项系数被墨水遮挡住了.
(1)她把被遮住的一次项系数猜成3,请你完成计算:????2+3????+2?????1;
(2)老师说:“你猜错了,这个题目的正确答案是不含一次项的,”请通过计算说明原题中被遮住的一次项系数是多少?
?
【详解】(1)解:????2+3????+2?????1=????3+3????2+2?????????2?3?????2=????3+2????2??????2;
(2)解:设第一次因式的一次项系数为a,则原题目变为????2+????????+2?????1,
????2+????????+2?????1=????3+????????2+2?????????2??????????2
=????3+?????1????2+2??????????2,
∵????2+????????+2?????1的计算结果不含一次项,∴2?????=0,
∴????=2,∴被遮住的一次项系数是2.
?
热考题型
考点一 整式的乘法
5.(23-24八年级上·河北邯郸·期末)发现:任意三个连续的奇数中,最大数与最小数的平方差是4的倍数.验证:
(1)92?52的结果是8的______倍;
(2)设三个连续的奇数中间的一个为2????+1(????为整数),计算最大奇数与最小奇数的平方差,并说明它是8的倍数.
?
【详解】(1)解:92?52=81?25=56,
56÷8=7,故答案为:7.
(2)解:由题意得,最大奇数为2????+3,最小奇数为2?????1,则:
2????+32?2?????12=2????+3+2?????12????+3?2????+1=44????+2=82????+1,
∵????为整数,∴2????+1为整数,
∴任意三个连续的奇数中,最大数与最小数的平方差是8的倍数.
?
热考题型
考点一 整式的乘法
6.(21-22七年级下·江苏无锡·期中)已知:????+?????????34的结果中不含关于字母x的一次项,求????+22?3???????????3的值.
?
【详解】解:????+?????????34
=????2+?????34?????34???? ,
∵结果中不含关于字母x的一次项,
∴????=34,
化简????+22?3???????????3可得:原式=4????+13,????????????
将????=34代入化简之后的式子得:4????+13=4×34+13=16.
?
热考题型
考点一 整式的乘法
7.(22-23七年级下·陕西西安·阶段练习)已知????2+3?????4=0,求代数式????+22?????3+2????????+6?????的值.
?
【详解】解:????+22?????3+2????????+6?????
=2????2?3????+4?????6+2????2+12?????????
=4????2+12?????6
∵????2+3?????4=0,∴????2+3????=4,
∴原式=4????2+3?????6
=4×4?6
=10
?
热考题型
考点一 整式的乘法
8.(23-24七年级下·陕西咸阳·阶段练习)如图,甲长方形的两邻边长分别为????+1,????+5,乙长方形的两邻边长分别为????+2,????+4.(其中????为正整数)
(1)图中甲长方形的面积为????1,乙长方形的面积为????2,比较大小:????1______????2(填“>”、“=”或“<”),并说明理由;
?
【详解】(1)解:<,
理由如下:????1?????2=????+1????+5?????+2????+4
=????2+6????+5?????2+6????+8
=????2+6????+5?????2?6?????8
=?3<0,
∴ ????1故答案为:<.
?
热考题型
考点一 整式的乘法
8.(23-24七年级下·陕西咸阳·阶段练习)如图,甲长方形的两邻边长分别为????+1,????+5,乙长方形的两邻边长分别为????+2,????+4.(其中????为正整数)
(2)现有一正方形,其周长与图中甲长方形的周长相等,正方形的面积为????.若甲、乙两个长方形的面积????1,????2与正方形的面积????满足????1+????2=32????,求这个正方形的面积.
?
(2)解:∵正方形的周长与图中甲长方形的周长相等,
∴正方形的周长为2????+1+????+5=4????+12,
∴正方形的边长为????+3,
∴正方形的面积????=????+32=????2+6????+9.
∵ ????1+????2=32????,∴ ????2+6????+5+????2+6????+8=32????2+6????+9,
整理得????2+6????=1,∴ ????2+6????+9=1+9=10,
∴这个正方形的面积为10.
?
热考题型
考点一 整式的乘法
9.(22-23七年级下·陕西咸阳·阶段练习)定义新运算????????????????=??????????????????,如8732=8?27?3=6×4=24,那么2????+?????????2????3?????5?????????????化简的结果是(????)
A.2????2?3????????+6????2 B.2????2??????????6????2
C.?2????2+3????????+6????2 D.?2????2?????????+6????2
?
【详解】解:2????+?????????2????3?????5?????????????=2????+???????????????????2?????3?????5????
=????+2?????2????+3????
=?2????2?????????+6????2.
故选:D.
?
知识大全
考点二 乘法公式
易错易混
考点二 乘法公式
1.应用完全平方公式计算时,应注意以下几个问题:
①公式中的a,b可是单项式,也可以是多项式;
②对形如两数和(或差)的平方的计算,都可以用这个公式;
③对于三项的可以把其中的两项看做一项后,也可以用完全平方公式.
2.应用平方差公式计算时,应注意以下几个问题:
①左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
②右边是相同项的平方减去相反项的平方;
③公式中的a和b可以是具体数,也可以是单项式或多项式;
④对形如两数和与这两数差相乘的算式,都可以运用这个公式计算,且会比用多项式乘以多项式法则简便.
知识大全
考点二 乘法公式
完全平方公式的几何背景
1.意义:运用几何图形直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.
2. 常见验证完全平方公式的几何图形
结论:(a+b)2=a2+2ab+b2.(用大正方形的面积等于边长为a和边长为b的两个正方形与两个长宽分别是a,b的长方形的面积和作为相等关系)
知识大全
考点二 乘法公式
平方差公式的几何背景
1.意义:运用几何图形直观理解、解决平方差公式的推导过程,通过几何图形之间的数量关系对平方差公式做出几何解释.
2. 常见验证平方差公式的几何图形
结论:(a+b)(a-b)=a2-b2
热考题型
考点二 乘法公式
1.(22-23七年级下·浙江金华·期末)若????+????????+????能运用平方差公式计算,则????,????满足的条件可能是(????)
①????=????,????=????;②????=????,????=?????;③????=?????,????=????;④????=?????,????=?????.
A.①③ B.①④ C.②③ D.②④
?
【详解】解:∵????+????????+????能运用平方差公式计算,
∴????=????,????=?????或????=?????,????=????,故选:C.
?
2.(20-21七年级下·广东茂名·期中)下列多项式不是完全平方式的是(????).
A.????2?4?????4 B.14+????2+???? C.????2+2????????+????2 D.????2+4????+4
?
3.【易错常考】(21-22七年级下·江苏苏州·期中)若????2?2????+1????+144是完全平方式,则常数????的值为(????)
A.-11或13 B.11或-13 C.±11 D.±13
?
【详解】∵????2?2(????+1)????+144是完全平方式,∴????+1=±12,
解得:????=11或?13,故答案为B.
?
热考题型
考点二 乘法公式
4.(23-24六年级下·山东淄博·期中)利用乘法公式计算:
(1)?2022;
(2)1232?124×122.
?
【详解】(1)解:?2022=2022=200+22=2002+2×200×2+22=40000+800+4=40804;
(2)1232?124×122=1232?123+1×123?1 =1232?1232?12=1232?1232+1=1.
?
5.(湖南省长沙市明德教育集团2023-2024学年九年级下学期月考数学试题)先化简,后求值:?????2????2+?????2????????+2??????????????4????,其中????=1,????=?1.
?
【详解】
解:原式=????2?4????????+4????2+????2?4????2?????2+4????????=????2
当????=1,????=?1时,原式=1
?
热考题型
考点二 乘法公式
6.求值:(2+1)22+124+128+1216+1232+1264+1=
?
【详解】原式=(2?1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1).
=(22?1)(22+1)(24+?1)(28+1)(216+1)(232+1)(264+1)
=(264?1)(264+1)
=2128?1.
?
7.(23-24七年级下·宁夏银川·阶段练习)求值:
(1)已知????+????=5,????????=2,求????2+????2的值.
(2)已知????+????=10,????2+????2=6,求????????的值
?
【详解】(1)∵????+????2=????2+2????????+????2,????+????=5,????????=2,
∴52=????2+2×2+????2,
解得????2+????2=21;
(2)∵????+????2=????2+2????????+????2,????+????=10,????2+????2=6,
∴102=6+2????????,
解得????????=100?62=47.
?
热考题型
考点二 乘法公式
【详解】解:由A选项可得:?????????2+2????????=????2+????2,故本选项不符合题意;
由B选项可得:????+????2=?????????2+4????????,故本选项符合题意;
由C选项可得:????+????2=????2+????2+2????????,故本选项不符合题意;
由选项D可得:?????????2=????2?2????????+????2,故本选项不符合题意,
故选:B.
?
热考题型
考点二 乘法公式
9.(23-24八年级上·山东滨州·期末)如图,在边长为a的正方形上裁去边长为b的正方形.
(1)图1阴影面积是 ;
(2)图2是将图1中的阴影部分裁开,重新拼成梯形,根据图形可以得到乘法公式 ;
(3)运用得到的公式,计算:1?1221?1321?142?1?11002= .
?
【详解】(1)解:阴影面积是:????2?????2,故答案为:????2?????2;
(2)解:根据梯形的面积公式可知图2中阴影部分的面积为:2×12(????+????)(?????????)=(????+????)(?????????),
∴可以得到的乘法公式为????+?????????????=????2?????2,故答案为:????+?????????????=????2?????2;
?
热考题型
考点二 乘法公式
9.(23-24八年级上·山东滨州·期末)如图,在边长为a的正方形上裁去边长为b的正方形.
(3)运用得到的公式,计算:1?1221?1321?142?1?11002= .
?
(3)解:1?1221?1321?142?1?11002
=1?121+121?131+131?141+14?1?11001+1100
=12×32×23×43×34×54×?×99100×101100
=12×101100
=101200.
?
知识大全
考点三 因式分解
易错易混
考点三 因式分解
1.因式分解分解对象是多项式,分解结果必须是积的形式,且积的因式必须是整式,这三个要素缺一不可;
2.因式分解必须是恒等变形;
3.因式分解必须分解到每个因式都不能分解为止.
4.因式分解与整式乘法是互逆变形,因式分解是把和差化为积的形式,而整式乘法是把积化为和差的形式.
解题技巧
考点三 因式分解
因式分解的关键在于熟练掌握因式分解的两种基本方法:提取公因式法和公式法.因式分解的一般步骤:
热考题型
考点三 因式分解
1.(21-22七年级上·上海·期末)下列等式中:①????2?????2=????+?????????????;②30=2×3×5;③????2+????+1=????????+1+1;④????+????2=????2+2????????+????2,从左到右的变形是因式分解的有( )
A.1个 B.2个 C.3个 D.4个
?
【详解】解:①由因式分解的概念可得,????2?????2=????+?????????????是从左到右的变形是因式分解;
②30不是多项式,故30=2×3×5从左到右的变形不是因式分解;
③????2+????+1不是几个整式的乘积的形式,故????2+????+1=????????+1+1从左到右的变形不是因式分解;
④????+????2=????2+2????????+????2,从左到右的变形是整式乘法,故从左到右的变形不是因式分解,
故选:A.
?
热考题型
考点三 因式分解
2.(22-23七年级下·陕西西安·阶段练习)若6????2?19????+15=????????+????????????+????,则????????+????????的值为 .
?
【详解】解:∵6????2?19????+15=????????+????????????+????,
而????????+????????????+????=????????????2+????????????+????????????+????????=????????????2+????????+????????????+????????,
∴????????=6,????????=15,
∴????????+????????=6+15=21,
?
3.(22-23七年级下·江苏苏州·期中)因式分解????2+????????+????时,甲看错了a的值,分解的结果是????+6?????1,乙看错了b的值,分解的结果为?????2????+1,那么????2+????????+????分解因式正确的结果为 .
?
【详解】解:甲错了a的值,(????+6)(?????1)=????2+5?????6,∴????=?6,
乙看错了b的值,?????2????+1=????2??????2,∴????=?1,
∴????2+????????+????分解因式正确的结果:????2??????6=(?????3)(????+2).
?
热考题型
考点三 因式分解
4.(22-23七年级下·江苏南京·阶段练习)分解因式:
(1)9????2(2?????????)+(?????2????);
(2)(????2?????)2+14(?????????2)+24.
?
【详解】(1)
解:9????2(2?????????)+(?????2????)
=9????2(2?????????)?(2?????????)
=(9????2?1)(2?????????)
=(2?????????)(3????+1)(3?????1);
(2)
(????2?????)2+14(?????????2)+24
=(????2?????)2?14(????2?????)+24
=(????2??????2)(????2??????12)
=(?????2)(????+1)(?????4)(????+3).
?
热考题型
考点三 因式分解
7.(23-24八年级上·全国·课后作业)计算:
(1)2022+202×196+982.
(2)9992?998×1002.
?
【详解】(1)解:原式=2022+2×202×98+982=(202+98)2=3002=90000.
(2)解:原式=(1000?1)2?(1000?2)(1000+2)=10002?2×1000×1+1?10002+4=?2000+5=?1995.
?
8.(23-24七年级下·全国·假期作业)已知????,????,????为三角形????????????的三边长,且满足????2????2?????2????2=????4?????4,则三角形????????????的形状为(????)
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.锐角三角形
?
【详解】因为????2????2?????2????2=????4?????4,即????2????2?????2=????2+????2????2?????2,
所以????2+????2????2?????2?????2????2?????2=0,
????2?????2????2+????2+????2=0,????+?????????????????2+????2+????2=0.
因为????,????,????是三角形的三边长,所以????+????>0,????2+????2+????2>0,所以?????????=0,即????=????,
所以三角形????????????为等腰三角形.
?
谢谢!
串讲03 整式的乘除与
因式分解
解题技巧
01
02
04
05
03
目
录
易错易混
知识大全
思维导图
热考题型
思维导图
知识大全
考点一 整式的乘法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}整式的乘法
运算步骤说明
补充说明及注意事项
单项式乘单项式
①将单项式系数相乘作为积的系数;
②相同字母的因式,利用同底数幂的乘法,作为积的一个因式;
③单独出现的字母,连同它的指数,作为积的一个因式.
1)实质:乘法的交换律和同底数幂的乘法法则的综合应用.
2)单项式乘单项式所得结果仍是单项式 .
单项式乘多项式
①先用单项式和多项式的每一项分别相乘;
②再把所得的积相加.
1)单项式乘多项式实质上是转化为单项式乘以单项式
2)单项式乘多项式的结果是多项式,积的项数与原多项式的项数相同.
多项式乘多项式
①先用一个多项式的每一项与另一个多项式的每一项相乘,
②再把所得的积相加.
运用法则时应注意以下两点:
①相乘时,按一定的顺序进行,必须做到不重不漏;
②多项式与多项式相乘,多项式的每一项都应该带上它前面的正负号.且结果仍是多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.
热考题型
考点一 整式的乘法
1.(23-24八年级上·河南南阳·阶段练习)计算下列各题
(1)34??????????????2????????????3
(2)????+1?????6?1?????4?????
?
【详解】(1)34??????????????2????????????3
=34???????????????8????3????3????3
=?6????4????4????3+8????3????4????3;
(2)????+1?????6?1?????4?????
=????2?6????+?????6?4??????4????+????2
=????2?6????+?????6?4+????+4?????????2
=?10.
?
热考题型
考点一 整式的乘法
2.(23-24八年级上·重庆渝中·期中)若????????2?????+3?????2????=????3+5?????6对任意????都成立,则????+????= .
?
【详解】
解:????????2?????+3?????2????=????3+5?????6,
????3?????????+3?????2????=????3+5?????6,
????3+?????+3?????2????=????3+5?????6,
∵原式子对任意????都成立,
∴?????+3=5,?2????=?6,
解得:????=?2,????=3,
∴????+????=?2+3=1.
故答案为:1.
?
热考题型
考点一 整式的乘法
3.(23-24八年级上·河南周口·阶段练习)在计算2????+????????+????时,甲错把b看成了6,得到的结果是:2????2+8?????24;乙错把a看成了?????,得到的结果是:2????2+14????+20,求a、b的值.
?
【详解】解:因为甲错把b看成了6,
则2????+????????+6=2????2+12+????????+6????=2????2+8?????24,
可得:????=?4,
因为乙错把a看成了?????,
则:2?????????????+????=2????+4????+????=2????2+2????+4????+4????=2????2+14????+20,
得:????=5.
?
热考题型
考点一 整式的乘法
4.(22-23七年级下·全国·假期作业)小红准备完成题目:计算 ,她发现第一个因式的一次项系数被墨水遮挡住了.
(1)她把被遮住的一次项系数猜成3,请你完成计算:????2+3????+2?????1;
(2)老师说:“你猜错了,这个题目的正确答案是不含一次项的,”请通过计算说明原题中被遮住的一次项系数是多少?
?
【详解】(1)解:????2+3????+2?????1=????3+3????2+2?????????2?3?????2=????3+2????2??????2;
(2)解:设第一次因式的一次项系数为a,则原题目变为????2+????????+2?????1,
????2+????????+2?????1=????3+????????2+2?????????2??????????2
=????3+?????1????2+2??????????2,
∵????2+????????+2?????1的计算结果不含一次项,∴2?????=0,
∴????=2,∴被遮住的一次项系数是2.
?
热考题型
考点一 整式的乘法
5.(23-24八年级上·河北邯郸·期末)发现:任意三个连续的奇数中,最大数与最小数的平方差是4的倍数.验证:
(1)92?52的结果是8的______倍;
(2)设三个连续的奇数中间的一个为2????+1(????为整数),计算最大奇数与最小奇数的平方差,并说明它是8的倍数.
?
【详解】(1)解:92?52=81?25=56,
56÷8=7,故答案为:7.
(2)解:由题意得,最大奇数为2????+3,最小奇数为2?????1,则:
2????+32?2?????12=2????+3+2?????12????+3?2????+1=44????+2=82????+1,
∵????为整数,∴2????+1为整数,
∴任意三个连续的奇数中,最大数与最小数的平方差是8的倍数.
?
热考题型
考点一 整式的乘法
6.(21-22七年级下·江苏无锡·期中)已知:????+?????????34的结果中不含关于字母x的一次项,求????+22?3???????????3的值.
?
【详解】解:????+?????????34
=????2+?????34?????34???? ,
∵结果中不含关于字母x的一次项,
∴????=34,
化简????+22?3???????????3可得:原式=4????+13,????????????
将????=34代入化简之后的式子得:4????+13=4×34+13=16.
?
热考题型
考点一 整式的乘法
7.(22-23七年级下·陕西西安·阶段练习)已知????2+3?????4=0,求代数式????+22?????3+2????????+6?????的值.
?
【详解】解:????+22?????3+2????????+6?????
=2????2?3????+4?????6+2????2+12?????????
=4????2+12?????6
∵????2+3?????4=0,∴????2+3????=4,
∴原式=4????2+3?????6
=4×4?6
=10
?
热考题型
考点一 整式的乘法
8.(23-24七年级下·陕西咸阳·阶段练习)如图,甲长方形的两邻边长分别为????+1,????+5,乙长方形的两邻边长分别为????+2,????+4.(其中????为正整数)
(1)图中甲长方形的面积为????1,乙长方形的面积为????2,比较大小:????1______????2(填“>”、“=”或“<”),并说明理由;
?
【详解】(1)解:<,
理由如下:????1?????2=????+1????+5?????+2????+4
=????2+6????+5?????2+6????+8
=????2+6????+5?????2?6?????8
=?3<0,
∴ ????1故答案为:<.
?
热考题型
考点一 整式的乘法
8.(23-24七年级下·陕西咸阳·阶段练习)如图,甲长方形的两邻边长分别为????+1,????+5,乙长方形的两邻边长分别为????+2,????+4.(其中????为正整数)
(2)现有一正方形,其周长与图中甲长方形的周长相等,正方形的面积为????.若甲、乙两个长方形的面积????1,????2与正方形的面积????满足????1+????2=32????,求这个正方形的面积.
?
(2)解:∵正方形的周长与图中甲长方形的周长相等,
∴正方形的周长为2????+1+????+5=4????+12,
∴正方形的边长为????+3,
∴正方形的面积????=????+32=????2+6????+9.
∵ ????1+????2=32????,∴ ????2+6????+5+????2+6????+8=32????2+6????+9,
整理得????2+6????=1,∴ ????2+6????+9=1+9=10,
∴这个正方形的面积为10.
?
热考题型
考点一 整式的乘法
9.(22-23七年级下·陕西咸阳·阶段练习)定义新运算????????????????=??????????????????,如8732=8?27?3=6×4=24,那么2????+?????????2????3?????5?????????????化简的结果是(????)
A.2????2?3????????+6????2 B.2????2??????????6????2
C.?2????2+3????????+6????2 D.?2????2?????????+6????2
?
【详解】解:2????+?????????2????3?????5?????????????=2????+???????????????????2?????3?????5????
=????+2?????2????+3????
=?2????2?????????+6????2.
故选:D.
?
知识大全
考点二 乘法公式
易错易混
考点二 乘法公式
1.应用完全平方公式计算时,应注意以下几个问题:
①公式中的a,b可是单项式,也可以是多项式;
②对形如两数和(或差)的平方的计算,都可以用这个公式;
③对于三项的可以把其中的两项看做一项后,也可以用完全平方公式.
2.应用平方差公式计算时,应注意以下几个问题:
①左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
②右边是相同项的平方减去相反项的平方;
③公式中的a和b可以是具体数,也可以是单项式或多项式;
④对形如两数和与这两数差相乘的算式,都可以运用这个公式计算,且会比用多项式乘以多项式法则简便.
知识大全
考点二 乘法公式
完全平方公式的几何背景
1.意义:运用几何图形直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.
2. 常见验证完全平方公式的几何图形
结论:(a+b)2=a2+2ab+b2.(用大正方形的面积等于边长为a和边长为b的两个正方形与两个长宽分别是a,b的长方形的面积和作为相等关系)
知识大全
考点二 乘法公式
平方差公式的几何背景
1.意义:运用几何图形直观理解、解决平方差公式的推导过程,通过几何图形之间的数量关系对平方差公式做出几何解释.
2. 常见验证平方差公式的几何图形
结论:(a+b)(a-b)=a2-b2
热考题型
考点二 乘法公式
1.(22-23七年级下·浙江金华·期末)若????+????????+????能运用平方差公式计算,则????,????满足的条件可能是(????)
①????=????,????=????;②????=????,????=?????;③????=?????,????=????;④????=?????,????=?????.
A.①③ B.①④ C.②③ D.②④
?
【详解】解:∵????+????????+????能运用平方差公式计算,
∴????=????,????=?????或????=?????,????=????,故选:C.
?
2.(20-21七年级下·广东茂名·期中)下列多项式不是完全平方式的是(????).
A.????2?4?????4 B.14+????2+???? C.????2+2????????+????2 D.????2+4????+4
?
3.【易错常考】(21-22七年级下·江苏苏州·期中)若????2?2????+1????+144是完全平方式,则常数????的值为(????)
A.-11或13 B.11或-13 C.±11 D.±13
?
【详解】∵????2?2(????+1)????+144是完全平方式,∴????+1=±12,
解得:????=11或?13,故答案为B.
?
热考题型
考点二 乘法公式
4.(23-24六年级下·山东淄博·期中)利用乘法公式计算:
(1)?2022;
(2)1232?124×122.
?
【详解】(1)解:?2022=2022=200+22=2002+2×200×2+22=40000+800+4=40804;
(2)1232?124×122=1232?123+1×123?1 =1232?1232?12=1232?1232+1=1.
?
5.(湖南省长沙市明德教育集团2023-2024学年九年级下学期月考数学试题)先化简,后求值:?????2????2+?????2????????+2??????????????4????,其中????=1,????=?1.
?
【详解】
解:原式=????2?4????????+4????2+????2?4????2?????2+4????????=????2
当????=1,????=?1时,原式=1
?
热考题型
考点二 乘法公式
6.求值:(2+1)22+124+128+1216+1232+1264+1=
?
【详解】原式=(2?1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1).
=(22?1)(22+1)(24+?1)(28+1)(216+1)(232+1)(264+1)
=(264?1)(264+1)
=2128?1.
?
7.(23-24七年级下·宁夏银川·阶段练习)求值:
(1)已知????+????=5,????????=2,求????2+????2的值.
(2)已知????+????=10,????2+????2=6,求????????的值
?
【详解】(1)∵????+????2=????2+2????????+????2,????+????=5,????????=2,
∴52=????2+2×2+????2,
解得????2+????2=21;
(2)∵????+????2=????2+2????????+????2,????+????=10,????2+????2=6,
∴102=6+2????????,
解得????????=100?62=47.
?
热考题型
考点二 乘法公式
【详解】解:由A选项可得:?????????2+2????????=????2+????2,故本选项不符合题意;
由B选项可得:????+????2=?????????2+4????????,故本选项符合题意;
由C选项可得:????+????2=????2+????2+2????????,故本选项不符合题意;
由选项D可得:?????????2=????2?2????????+????2,故本选项不符合题意,
故选:B.
?
热考题型
考点二 乘法公式
9.(23-24八年级上·山东滨州·期末)如图,在边长为a的正方形上裁去边长为b的正方形.
(1)图1阴影面积是 ;
(2)图2是将图1中的阴影部分裁开,重新拼成梯形,根据图形可以得到乘法公式 ;
(3)运用得到的公式,计算:1?1221?1321?142?1?11002= .
?
【详解】(1)解:阴影面积是:????2?????2,故答案为:????2?????2;
(2)解:根据梯形的面积公式可知图2中阴影部分的面积为:2×12(????+????)(?????????)=(????+????)(?????????),
∴可以得到的乘法公式为????+?????????????=????2?????2,故答案为:????+?????????????=????2?????2;
?
热考题型
考点二 乘法公式
9.(23-24八年级上·山东滨州·期末)如图,在边长为a的正方形上裁去边长为b的正方形.
(3)运用得到的公式,计算:1?1221?1321?142?1?11002= .
?
(3)解:1?1221?1321?142?1?11002
=1?121+121?131+131?141+14?1?11001+1100
=12×32×23×43×34×54×?×99100×101100
=12×101100
=101200.
?
知识大全
考点三 因式分解
易错易混
考点三 因式分解
1.因式分解分解对象是多项式,分解结果必须是积的形式,且积的因式必须是整式,这三个要素缺一不可;
2.因式分解必须是恒等变形;
3.因式分解必须分解到每个因式都不能分解为止.
4.因式分解与整式乘法是互逆变形,因式分解是把和差化为积的形式,而整式乘法是把积化为和差的形式.
解题技巧
考点三 因式分解
因式分解的关键在于熟练掌握因式分解的两种基本方法:提取公因式法和公式法.因式分解的一般步骤:
热考题型
考点三 因式分解
1.(21-22七年级上·上海·期末)下列等式中:①????2?????2=????+?????????????;②30=2×3×5;③????2+????+1=????????+1+1;④????+????2=????2+2????????+????2,从左到右的变形是因式分解的有( )
A.1个 B.2个 C.3个 D.4个
?
【详解】解:①由因式分解的概念可得,????2?????2=????+?????????????是从左到右的变形是因式分解;
②30不是多项式,故30=2×3×5从左到右的变形不是因式分解;
③????2+????+1不是几个整式的乘积的形式,故????2+????+1=????????+1+1从左到右的变形不是因式分解;
④????+????2=????2+2????????+????2,从左到右的变形是整式乘法,故从左到右的变形不是因式分解,
故选:A.
?
热考题型
考点三 因式分解
2.(22-23七年级下·陕西西安·阶段练习)若6????2?19????+15=????????+????????????+????,则????????+????????的值为 .
?
【详解】解:∵6????2?19????+15=????????+????????????+????,
而????????+????????????+????=????????????2+????????????+????????????+????????=????????????2+????????+????????????+????????,
∴????????=6,????????=15,
∴????????+????????=6+15=21,
?
3.(22-23七年级下·江苏苏州·期中)因式分解????2+????????+????时,甲看错了a的值,分解的结果是????+6?????1,乙看错了b的值,分解的结果为?????2????+1,那么????2+????????+????分解因式正确的结果为 .
?
【详解】解:甲错了a的值,(????+6)(?????1)=????2+5?????6,∴????=?6,
乙看错了b的值,?????2????+1=????2??????2,∴????=?1,
∴????2+????????+????分解因式正确的结果:????2??????6=(?????3)(????+2).
?
热考题型
考点三 因式分解
4.(22-23七年级下·江苏南京·阶段练习)分解因式:
(1)9????2(2?????????)+(?????2????);
(2)(????2?????)2+14(?????????2)+24.
?
【详解】(1)
解:9????2(2?????????)+(?????2????)
=9????2(2?????????)?(2?????????)
=(9????2?1)(2?????????)
=(2?????????)(3????+1)(3?????1);
(2)
(????2?????)2+14(?????????2)+24
=(????2?????)2?14(????2?????)+24
=(????2??????2)(????2??????12)
=(?????2)(????+1)(?????4)(????+3).
?
热考题型
考点三 因式分解
7.(23-24八年级上·全国·课后作业)计算:
(1)2022+202×196+982.
(2)9992?998×1002.
?
【详解】(1)解:原式=2022+2×202×98+982=(202+98)2=3002=90000.
(2)解:原式=(1000?1)2?(1000?2)(1000+2)=10002?2×1000×1+1?10002+4=?2000+5=?1995.
?
8.(23-24七年级下·全国·假期作业)已知????,????,????为三角形????????????的三边长,且满足????2????2?????2????2=????4?????4,则三角形????????????的形状为(????)
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.锐角三角形
?
【详解】因为????2????2?????2????2=????4?????4,即????2????2?????2=????2+????2????2?????2,
所以????2+????2????2?????2?????2????2?????2=0,
????2?????2????2+????2+????2=0,????+?????????????????2+????2+????2=0.
因为????,????,????是三角形的三边长,所以????+????>0,????2+????2+????2>0,所以?????????=0,即????=????,
所以三角形????????????为等腰三角形.
?
谢谢!
同课章节目录
