1.章末总结 课件(共31张PPT)——高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 1.章末总结 课件(共31张PPT)——高中数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 646.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
章末总结
1
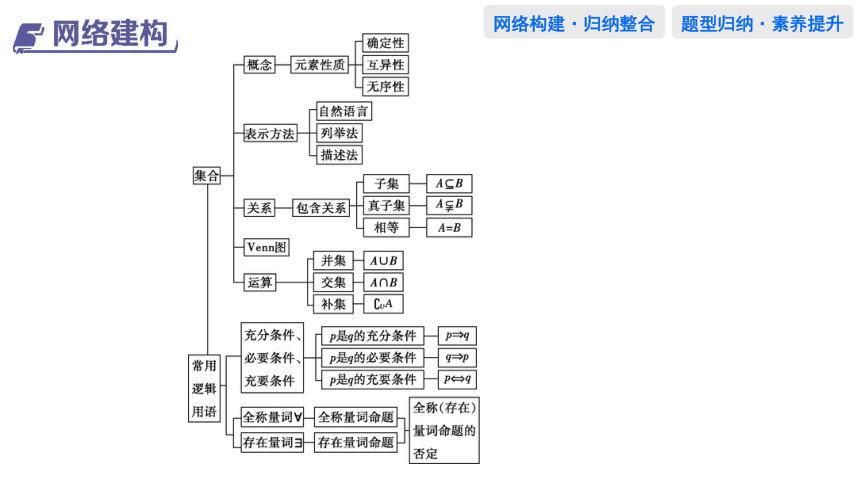
网络构建
归纳整合
判断对错(正确的打“√”,错误的打“×”).
1. NN*={0}, ZN={负整数}, RQ={无理数}.( )
3.A B x∈A是x∈B的充分条件 x∈B是x∈A的必要条件.( )
√
√
√
4.“A∩B=A∩C”是“B=C”的充分不必要条件.( )
5.若命题“若p,则q”为真命题,则“若p,则﹁q”为假命题.( )
6.若命题“ x∈M,p(x)”为真命题,则“ x∈M,﹁p(x)”为假命题.( )
×
√
√
2
题型归纳
素养提升
题型一 集合的基本概念
√
解析:(1)集合元素要满足互异性,当a=0时,该集合为{1,3,0}符合,当a=3时,该集合为{1,3,9}符合,其他均不符合.故选C.
(2)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9 B.8 C.5 D.4
√
解析:(2)因为x2+y2≤3,所以x2≤3,
因为x∈Z,所以x=-1,0,1
当x=-1时,y=-1,0,1;
当x=0时,y=-1,0,1;
当x=1时,y=-1,0,1,所以共有9个.故选A.
与集合中的元素有关问题的求解策略
(1)确定集合的元素是什么,即集合是数集还是点集.
(2)看这些元素满足什么限制条件.
(3)根据限制条件列式求参数的值或确定集合中元素的个数时,要注意检验集合是否满足元素的互异性.
题型二 集合间的基本关系
√
{m|m≤4}
(2)已知集合A={x|-2≤x≤7},B={x|m+1(1)空集是任何集合的子集,在涉及集合关系时要优先考虑空集的情况,否则会造成漏解.
(2)端点值:已知两集合间的关系求参数的取值范围,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的条件,常用数轴解决此类问题.
题型三 集合的基本运算
√
法二 观察选项进行特取,取x=4,
则4∈M,4∈N,
所以4∈(M∩N),排除A,B;取x=1,
则1∈M,1∈N,所以1∈(M∩N),排除C.故选D.
(2)(2022·全国甲卷)设全集U={-2,-1,0,1,2,3},集合A={-1,2},B={x|x2-4x+3=0},则 U(A∪B)等于( )
A.{1,3} B.{0,3}
C.{-2,1} D.{-2,0}
解析:(2)集合B={1,3},所以A∪B={-1,1,2,3},所以 U(A∪B)={-2,0}.故选D.
√
(3)(2022·新高考Ⅱ卷)已知集合A={-1,1,2,4},B=
{x||x-1|≤1},则A∩B等于( )
A.{-1,2} B.{1,2}
C.{1,4} D.{-1,4}
√
解析:(3)法一 由|x-1|≤1,得-1≤x-1≤1,解得0≤x≤2,所以B={x|0≤x≤2},所以A∩B={1,2}.故选B.
法二 因为4 B,所以4 A∩B,故排除C,D;又-1 B,
所以-1 A∩B,故排除A.故选B.
√
(5)设M,N,U均为非空集合,且满足M N U,则( UM)∩( UN)等于( )
A.M B.N
C. UM D. UN
√
解析:(5)集合M,N,U的Venn图,如图所示,
因为M N U,所以 UN UM,
所以( UM)∩( UN)= UN.故选D.
(1)集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.
(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图.
题型四 充分条件、必要条件与充要条件
[例4] (1)设x,y都是实数,则“x>2,且y>3”是“x>2或y>3”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
√
(2)已知a∈R,则“a≤2”是“|x-2|+|x|>a恒成立”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
√
解析:(2)根据绝对值的几何意义,|x-2|表示数轴上的点x与点2的距离,|x|表示数轴上点x与原点的距离,所以|x-2|+|x|≥2,所以a<2,而{a|a<2} {a|a≤2},故“a≤2”是“a<2”的必要不充分条件.故选B.
(1)充分条件与必要条件的判定方法.
①定义法:直接判断若q则p的真假.
②利用集合间的包含关系判断:若A B,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.
(2)利用充分条件和必要条件求参数的取值范围,主要是根据集合间的包含关系与充分条件和必要条件的关系,将问题转化为集合之间的关系,建立关于参数的不等式或不等式组求解.
题型五 全称量词与存在量词
[例5] (1)十七世纪,数学家费马提出猜想:“对任意正整数n>2,关于x,y,z的方程xn+yn=zn没有正整数解”,经历三百多年,1995年数学家安德鲁·怀尔斯给出了证明,使它终成费马大定理,则费马大定理的否定为( )
A.对任意正整数n,关于x,y,z的方程xn+yn=zn都没有正整数解
B.对任意正整数n>2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解
C.存在正整数n≤2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解
D.存在正整数n>2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解
√
解析:(1)命题为全称量词命题,
则命题的否定为“存在正整数n>2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解”.故选D.
(2)已知命题p: x∈R,x2+x-a>0为假命题,则实数a的取值范围是 .
(1)已知含量词的命题的真假求参数的取值范围,实质上是对命题意义的考查.解决此类问题,一定要辨清参数,恰当选取主元,合理确定解题思路.
(2)解决此类问题的关键是根据含量词命题的真假转化为相关数学知识,利用函数、方程、不等式等知识求解参数的取值范围,解题过程中要注意变量取值范围的限制.
章末总结
1
网络构建
归纳整合
判断对错(正确的打“√”,错误的打“×”).
1. NN*={0}, ZN={负整数}, RQ={无理数}.( )
3.A B x∈A是x∈B的充分条件 x∈B是x∈A的必要条件.( )
√
√
√
4.“A∩B=A∩C”是“B=C”的充分不必要条件.( )
5.若命题“若p,则q”为真命题,则“若p,则﹁q”为假命题.( )
6.若命题“ x∈M,p(x)”为真命题,则“ x∈M,﹁p(x)”为假命题.( )
×
√
√
2
题型归纳
素养提升
题型一 集合的基本概念
√
解析:(1)集合元素要满足互异性,当a=0时,该集合为{1,3,0}符合,当a=3时,该集合为{1,3,9}符合,其他均不符合.故选C.
(2)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9 B.8 C.5 D.4
√
解析:(2)因为x2+y2≤3,所以x2≤3,
因为x∈Z,所以x=-1,0,1
当x=-1时,y=-1,0,1;
当x=0时,y=-1,0,1;
当x=1时,y=-1,0,1,所以共有9个.故选A.
与集合中的元素有关问题的求解策略
(1)确定集合的元素是什么,即集合是数集还是点集.
(2)看这些元素满足什么限制条件.
(3)根据限制条件列式求参数的值或确定集合中元素的个数时,要注意检验集合是否满足元素的互异性.
题型二 集合间的基本关系
√
{m|m≤4}
(2)已知集合A={x|-2≤x≤7},B={x|m+1
(2)端点值:已知两集合间的关系求参数的取值范围,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的条件,常用数轴解决此类问题.
题型三 集合的基本运算
√
法二 观察选项进行特取,取x=4,
则4∈M,4∈N,
所以4∈(M∩N),排除A,B;取x=1,
则1∈M,1∈N,所以1∈(M∩N),排除C.故选D.
(2)(2022·全国甲卷)设全集U={-2,-1,0,1,2,3},集合A={-1,2},B={x|x2-4x+3=0},则 U(A∪B)等于( )
A.{1,3} B.{0,3}
C.{-2,1} D.{-2,0}
解析:(2)集合B={1,3},所以A∪B={-1,1,2,3},所以 U(A∪B)={-2,0}.故选D.
√
(3)(2022·新高考Ⅱ卷)已知集合A={-1,1,2,4},B=
{x||x-1|≤1},则A∩B等于( )
A.{-1,2} B.{1,2}
C.{1,4} D.{-1,4}
√
解析:(3)法一 由|x-1|≤1,得-1≤x-1≤1,解得0≤x≤2,所以B={x|0≤x≤2},所以A∩B={1,2}.故选B.
法二 因为4 B,所以4 A∩B,故排除C,D;又-1 B,
所以-1 A∩B,故排除A.故选B.
√
(5)设M,N,U均为非空集合,且满足M N U,则( UM)∩( UN)等于( )
A.M B.N
C. UM D. UN
√
解析:(5)集合M,N,U的Venn图,如图所示,
因为M N U,所以 UN UM,
所以( UM)∩( UN)= UN.故选D.
(1)集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.
(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图.
题型四 充分条件、必要条件与充要条件
[例4] (1)设x,y都是实数,则“x>2,且y>3”是“x>2或y>3”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
√
(2)已知a∈R,则“a≤2”是“|x-2|+|x|>a恒成立”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
√
解析:(2)根据绝对值的几何意义,|x-2|表示数轴上的点x与点2的距离,|x|表示数轴上点x与原点的距离,所以|x-2|+|x|≥2,所以a<2,而{a|a<2} {a|a≤2},故“a≤2”是“a<2”的必要不充分条件.故选B.
(1)充分条件与必要条件的判定方法.
①定义法:直接判断若q则p的真假.
②利用集合间的包含关系判断:若A B,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.
(2)利用充分条件和必要条件求参数的取值范围,主要是根据集合间的包含关系与充分条件和必要条件的关系,将问题转化为集合之间的关系,建立关于参数的不等式或不等式组求解.
题型五 全称量词与存在量词
[例5] (1)十七世纪,数学家费马提出猜想:“对任意正整数n>2,关于x,y,z的方程xn+yn=zn没有正整数解”,经历三百多年,1995年数学家安德鲁·怀尔斯给出了证明,使它终成费马大定理,则费马大定理的否定为( )
A.对任意正整数n,关于x,y,z的方程xn+yn=zn都没有正整数解
B.对任意正整数n>2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解
C.存在正整数n≤2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解
D.存在正整数n>2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解
√
解析:(1)命题为全称量词命题,
则命题的否定为“存在正整数n>2,关于x,y,z的方程xn+yn=zn至少存在一组正整数解”.故选D.
(2)已知命题p: x∈R,x2+x-a>0为假命题,则实数a的取值范围是 .
(1)已知含量词的命题的真假求参数的取值范围,实质上是对命题意义的考查.解决此类问题,一定要辨清参数,恰当选取主元,合理确定解题思路.
(2)解决此类问题的关键是根据含量词命题的真假转化为相关数学知识,利用函数、方程、不等式等知识求解参数的取值范围,解题过程中要注意变量取值范围的限制.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
