2024年辽宁中考数学二轮专题复习 微专题 二次函数与等腰三角形问题 课件(共58张PPT)
文档属性
| 名称 | 2024年辽宁中考数学二轮专题复习 微专题 二次函数与等腰三角形问题 课件(共58张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 07:00:25 | ||
图片预览








文档简介
(共58张PPT)
例1题图
微技能——分类讨论思想确定动点位置
一阶
一题多设问
例1 已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C.连接AC.
微专题:二次函数与等腰三角形问题
探究1:在抛物线对称轴上找一点P使得△ACP为等腰三角形.
(1)若AC为等腰三角形的底边时,AP=PC;在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例1题解图①
解:探究1:(1)满足条件的点P如解图①所示.
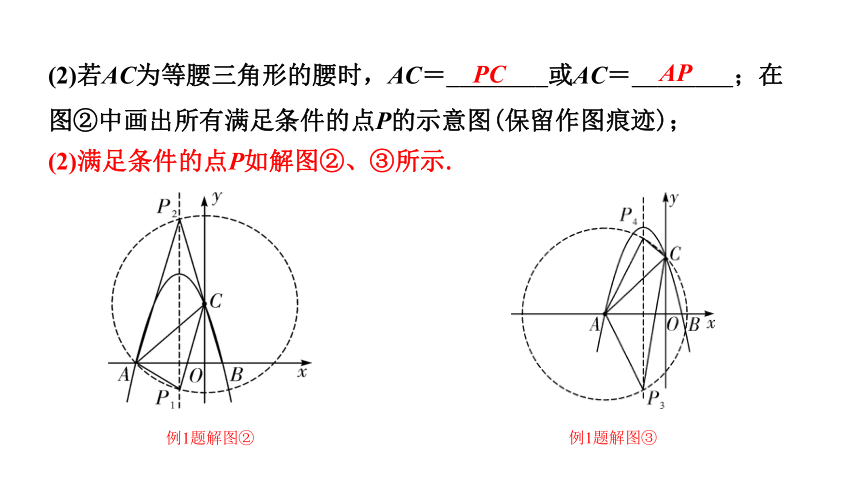
(2)若AC为等腰三角形的腰时,AC=________或AC=________;在图②中画出所有满足条件的点P的示意图(保留作图痕迹);
PC
AP
(2)满足条件的点P如解图②、③所示.
例1题解图②
例1题解图③
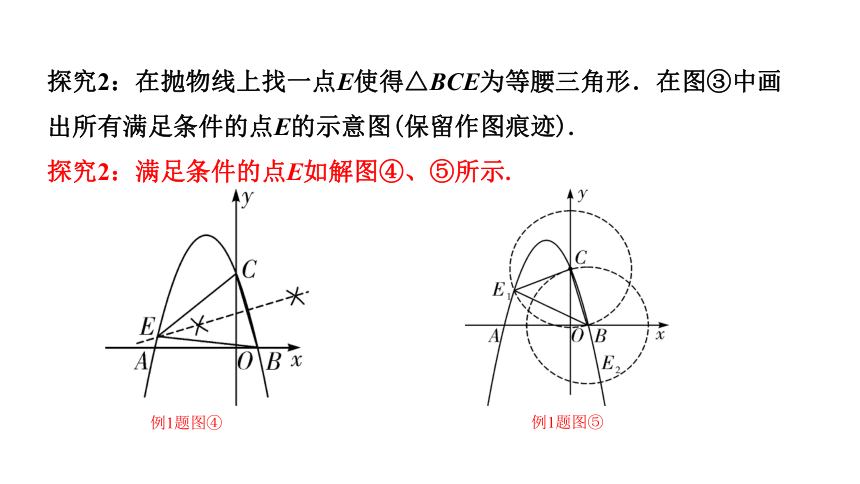
探究2:在抛物线上找一点E使得△BCE为等腰三角形.在图③中画出所有满足条件的点E的示意图(保留作图痕迹).
例1题图④
探究2:满足条件的点E如解图④、⑤所示.
例1题图⑤
【作图依据】______________________________________________
线段垂直平分线上的点到线段两端点的距离相等.
【方法总结】等腰三角形的存在性一般要分情况讨论:常以已知边为______或______讨论;以探究1为例,已知边AC为底时,可以作已知边的______________________,所找点即为__________________的交点;若已知边AC为腰时,作图方法为:_______________________________,所找点即为____________________
腰
底边
垂直平分线(中垂线)
垂直平分线和对称轴
圆与对称轴的交点.
AC的长为半径画圆
分别以点A、C为圆心,
三点共线时,不能构成三角形,须忽略.
●
易错警示
【思考】若动点在y轴上、x轴上时,确定动点位置有什么不同呢?
一题多设问
二阶
一题多设问
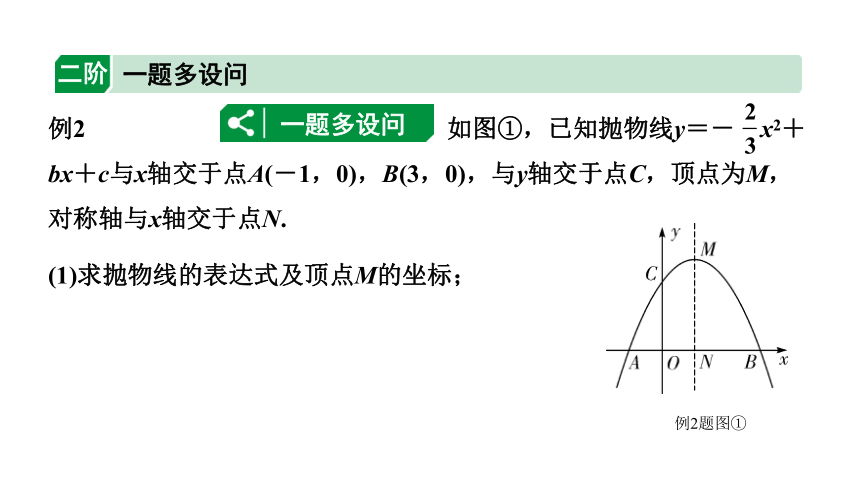
例2 如图①,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,顶点为M,对称轴与x轴交于点N.
例2题图①
(1)求抛物线的表达式及顶点M的坐标;
∴抛物线的表达式为y=- x2+ x+2
∴抛物线的对称轴为直线x= =
当x=1时,y=
∴顶点M的坐标为(1, );
解:(1)将点A(-1,0),B(3,0)代入抛物线y=- x2+bx+c中,
得 解得
例2题图①
例2题图②
(2)如图②,点P是抛物线上一点,当△PCO是以OC为底边的等腰三角形时,请直接写出点P的横坐标;
【思维教练】由于点P在抛物线上,△PCO是以OC为底边的等腰三角形,所以点P在OC的垂直平分线与抛物线的交点上.
例2题图②
令x=0,则y=2,∴C(0,2),∴OC=2,
∵△COP是以CO为底的等腰三角形,
∴CD=DO=1,
∴点P,P′的纵坐标为1,
当y=1时,- x2+ x+2=1,
P
P′
D
【解法提示】如解图①,作CO的垂直平分线交抛物线于点P和点P′,交CO于点D.连接CP、OP,OP′,CP′,△POC和△P′CO是以OC为底的等腰三角形.
解得x=1+ 或x=1- .
∴点P的横坐标为1+ ,
点P′的横坐标为1- .
即存在点P使△PCO是以OC为底边的等腰三角形,点P的横坐标为
1+ 或1- .
(2)点P的横坐标为1+ 或1-
例2题图②
P
P′
D
例2题图③
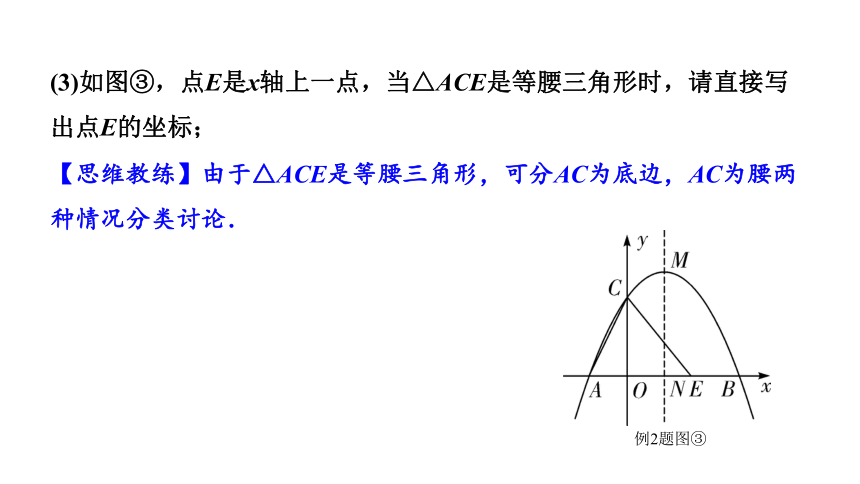
(3)如图③,点E是x轴上一点,当△ACE是等腰三角形时,请直接写出点E的坐标;
【思维教练】由于△ACE是等腰三角形,可分AC为底边,AC为腰两种情况分类讨论.
【解法提示】∵点E在x轴上,
∴设点E的坐标为(m,0).由(1)易得点C的坐标为(0,2),
∴AC= ,
∵△ACE是等腰三角形,
①当AE=AC时,
ⅰ.当点E在点A的右侧时,
∵AE=AC= ,
则EO= -1,
例2题图③
∴E的横坐标为 -1;
∴E( -1,0);
ⅱ.当点E在点A的左侧时,
∵AE=AC= ,则EO= +1,
∴点E的横坐标是- -1;
∴E(- -1,0);
②当AC=CE时,∵CO⊥AE,
∴点E在AO的延长线上,且AO=EO,
∴点E的横坐标为1;∴E(1,0);
例2题图③
③当AC为底时,则AE=CE时,则点E为AC的垂直平分线与x轴的交点.
∵AE=1+m,OE=m,
∴AE2=(1+m)2.
∵点C的坐标为(0,2),
∴OC=2.
∴CE2=m2+22.
∵CE=AE,∴22+m2=(1+m)2,
解得m=
例2题图③
∴E( ,0),
综上所述,点E的坐标为( -1,0)或(- -1,0)或(1,0)或
( ,0).
(3)点E的坐标为( -1,0)或(- -1,0)或(1,0)或( ,0);
例2题图③
例2题图④
(4)如图④,对称轴MN上一点是否存在点G,使得△CGB是等腰三角形,若存在,请直接写出点G的纵坐标;若不存在,请说明理由;
【思维教练】未明确说等腰三角形的腰和底,故要分类讨论:①CG=CB,②CG=BG,③BG=BC求解即可.
【解法提示】∵点G在对称轴上,∴设点G的坐标为(1,m),
∵点C(0,2),B(3,0),
∴BC2=22+32=13,CG2=1+(m-2)2,BG2=22+m2,
当△CGB是等腰三角形时,可分以下三种情况:
①当CG=CB时,1+(m-2)2=13,解得m=2+2 或m=2-2 ,
∴G(1,2+2 )或(1,2-2 );
②当CG=BG时,1+(m-2)2=22+m2,解得m= ,∴G(1, );
③当BG=BC时,22+m2=13,解得m=3或m=-3,
∴G(1,3)或(1,-3);
综上所述,当△CGB是等腰三角形时,点G的纵坐标为2+2 或
2-2 或 或3或-3.
(4)存在,点G的纵坐标为2+2 或2-2 或 或3或-3;
例2题图⑤
(5)如图⑤,点D的坐标为(4,0),动点Q从点A开始沿AC方向以每秒
个单位长度的速度运动,动点P从点C开始,沿CD方向以每秒 个单位长度的速度运动,当点Q到达终点时,两点同时停止运动.设运动时间为t,当△NPQ是等腰三角形时,请直接写出t的值.
【思维教练】根据题意用含t的式子表示出
QN,PQ,PN,由于不确定△NPQ的底和腰.
所以分下列三种情况讨论:
①NQ=NP,②NQ=PQ,③NP=PQ求解即可.
例2题图⑤
【解法提示】由点的坐标易得AC= ,CD=2 ,AD=5.
由勾股定理逆定理得AC2+CD2=AD2,∴∠ACD=90°.
根据题意可知,AQ= t,CP= t,∴CQ= - t,
∴PQ2=CQ2+CP2=( - t)2+( t)2= t2-5t+5,
Q
G
H
P
易得AG= t,QG=t,∴NG=2- t,
则NQ2=QG2+NG2= t2-2t+4,
同理可得NP2=5t2-8t+5,
其中t的取值范围是0≤t≤2.
如解图②,过点Q作QG⊥x轴于点G,过点P作PH⊥x轴于点H,
当△NPQ是等腰三角形时,则分以下几种情况:
①当NQ=NP时, t2-2t+4=5t2-8t+5,
整理得15t2-24t+4=0,解得t= 或t= ;
②当NQ=PQ时, t2-2t+4= t2-5t+5,
整理得5t2-3t+1=0,此方程无解,则此时t不存在;
例2题图⑤
Q
G
H
P
③当NP=PQ时,5t2-8t+5= t2-5t+5,
整理得5t2+12t=0,解得t=0或t=- (舍去).
综上所述,当△NPQ是等腰三角形时,t的值为 或 或0.
(5)t的值为 或 或0.
例2题图⑤
Q
G
H
P
综合训练
三阶
1.(2023抚顺新抚区一模)如图,直线y=- x+2与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A,B两点,P为x轴上的动点,P与A,O不重合,PC∥OB交抛物线于C,交直线AB于D,连接BC.
(1)求抛物线的解析式;
第1题图
备用图
解:(1)∵直线y=- x+2与x轴交于点A,与y轴交于点B,
当y=0时,x=4,
∴点A的坐标是(4,0),
当x=0时,y=2,
∴点B的坐标是(0,2),
又∵抛物线y=-x2+bx+c经过A,B两点,
∴ ,解得,
∴抛物线的解析式是y=-x2+ x+2;
第1题图
(2)当∠BCD=45°时,求点P的坐标;
(2)设点C的坐标是(x,y),当点C在第一象限时,
∵∠BCD=45°,
∴y-2=x,
∴y=-x2+ x+2=x+2,
∴x1= ,x2=0(不合题意,舍去),
∴点P的坐标是( ,0),
当点C在第四象限时,2-y=x,
∴y=-x2+ x+2=-x+2,
∴x1= ,x2=0(不合题意,舍去),
∴点P的坐标是 ( ,0),
综上所述,点P的坐标是( ,0)或( ,0);
第1题图
(3)当△BCD为等腰三角形时,直接写出点P的坐标.
E
则点E是等腰三角形△BCD的边DC中点,
则有yE= (yC+yD),
即2= (-m2+ m+2- m+2),
解得m1=3,m2=0(不合题意,舍去),
此时点P的坐标是(3,0);
【解法提示】设点P的坐标是(m,0),则点D的坐标是(m,- m+2),
当0<m<4时,若△BCD为等腰三角形时,则有以下情况:
①如解图①,当BC=BD时,过点B作BE⊥CD交CD于点E,
②当BC=CD时,
BC= , = =
CD=yC-yD=(-m2+ m+2)-(- m+2)=-m2+4m,
∵BC2=CD2,
∴m2(m2-7m+ )=m2(m2-8m+16),
解得m1= ,m2=0(不合题意,舍去),
∴此时点P的坐标是( ,0);
第1题图
E
第1题解图②
③当BD=CD时,
BD= = ,
CD=yC-yD=(-m2+ m+2)-(- m+2)=-m2+4m,
∴ m=-m2+4m,
解得m1= ,m2=0(不合题意,舍去),
∴此时点P的坐标是( ,0),
当m>4时,只有BD=CD,才能使△BCD为等腰三角形,如解图②,
则有CD=yD-yC=(- m+2)-(-m2+ m+2)=m2-4m,
解之得:m1= ,m2=0(舍去),
∴此时点P的坐标是( ,0);
综上所述,点P的坐标是(3,0)或( ,0)或( ,0)或P4( ,0).
(3)点P的坐标为(3,0)或( ,0)或( ,0)或( ,0).
∴ m=m2-4m,
第1题解图②
第2题图
2.如图,在平面直角坐标系中,抛物线y=ax2-x+c(a≠0)与x轴交于A(-1,0)、B(3,0)两点,直线AC与y轴交于点C,与抛物线交于点D,OA=OC.
(1)求该抛物线与直线AC的解析式;
备用图
解:(1)把A(-1,0)、B(3,0)代入y=ax2-x+c,得
解得
∴抛物线的解析式为y= x2-x- ;
∵OC=OA=1,
∴C(0,1),
设直线AC的解析式为y=kx+1(k≠0),则-k+1=0,解得k=1,
∴直线AC的解析式为y=x+1
设E(x, x2-x- )(-1<x<3),则G(x,x+1),
∴EG=x+1-( x2-x- )=- x2+2x+ .
∵OA=OC=1,∠AOC=90°,
∴∠OCA=45°,AC= = ,
第2题图
(2)若点E是x轴下方抛物线上一动点,连接AE、CE.求△ACE面积的最大值及此时点E的坐标;
(2)如解图①,作EG⊥x轴交直线AC于点G,作EH⊥AD于点H.
G
H
∵∠HGE=∠OCA=45°,
∴EH=EG·sin45°= (- x2+2x+ ),
第2题图
G
H
∴S△ACE= = =
∵ <0,且-1<2<3,
∴当x=2时,S△ACE最大= ,
此时E(2, ).
∴△ACE面积的最大值为 ,此时点E的坐标为(2, );
(3)将原抛物线沿射线AD方向平移2 个单位长度,得到新抛物线:y1=a1x2+b1x+c1(a≠0),新抛物线与原抛物线交于点F,在直线AD上是否存在点P,使以点P、D、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
第2题图
备用图
第2题解图②
【解法提示】如解图②,在直线AC上取一点A′,使它的横坐标为1,则A′(1,2),AA′= = ,
∴点A′即为抛物线平移后点A的对应点,
可知抛物线向右、向上各平移2个单位长度.
∵
∴平移后的抛物线为 ,其顶点坐标为(3,0);
∵原抛物线与新抛物线都经过点B(3,0),
∴点B即为新抛物线与原抛物线的交点F.
作A′K⊥x轴于点K,则∠AKA′=∠FKA′=90°,AK=A′K=FK=2,
∴∠AA′K=∠FA′K=45°,
∴∠AA′F=90°.
由 ,解得 或 (不符合题意,舍去)
∴D(5,6),
∴FD= .
①当FP1=FD时,则点P1与点D关于点A′对称,
∴P1(-3,-2);
②当P2D=FD= 时,
∵CD= ×5=5 ,
∴CP2= - ,
∴xp= ,yp= ,
P2( , );
第2题解图②
③当DP3=FP3时,
∵∠P3DF=∠FDP1,∠DFP3=∠DP1F,
∴△P3DF∽△FDP1,∴ ,
∵DP1= ×(5+3)=8 ,
∴ ,
∴CP3= ,
∴xp= ,yp= ,∴P3( , );
第2题解图②
④当P4D=FD=2 时,则CP4= ,
∴xp= ,
yp= ,
∴P4( , ).
综上所述,点P的坐标为(-3,-2)或( , )或( , )或( , ).
(3)存在,点P的坐标为(-3,-2)或( , )或( , )或
( , ).
第3题图
3.如图,抛物线y=ax2+x+c与x轴交于A,B(4,0)两点(点A在点B的左侧),与y轴交于点C(0,4),直线BC经过B,C两点,点P是第一象限内抛物线上的一个动点,连接PB,PC.
(1)求抛物线的函数表达式;
解:(1)由题意,将B(4,0),C(0,4)代入抛物线
y=ax2+x+c,得 解得
∴抛物线的函数表达式为y=- x2+x+4;
第3题图
第3题图
(2)设点P的横坐标为n,四边形OBPC的面积为S,求S的最大值并求出此时点P的坐标;
(2)如解图①,过点P作PE⊥x轴于点E,交BC于点F.
∵B(4,0),C(0,4),
∴OB=OC=4.
易得直线BC的表达式为y=-x+4.
∵点P的横坐标为n,
∴P(n,- n2+n+4),F(n,-n+4).
∴PF=- n2+n+4-(-n+4)=- n2+2n,
E
F
∴S四边形OBPC=S△BOC+S△PBF+S△PCF= = =
= ×4×4+ ×( n2+2n)×4=-n2+4n+8=-(n-2)2+12
∵-1<0,0<n<4.
∴当n=2时,S有最大值,S最大=12,
此时- n2+n+4=- ×22+2+4=4,
∴此时点P的坐标为(2,4);
第3题图
E
F
第3题图
(3)在(2)的条件下,当S取最大值时,在PC的垂直平分线上是否存在一点M,使△BPM是等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【解法提示】∵P(2,4),C(0,4),
∴PC∥x轴,PC=2,
∴PC的垂直平分线⊥x轴且为直线x=1,
∴点M的横坐标为1,
∴可设点M的坐标为(1,y).
又∵B(4,0),P(2,4),
∴PM2=(1-2)2+(y-4)2=y2-8y+17,
MB2=(1-4)2+y2=y2+9,
PB2=(4-2)2+(0-4)2=20.
当△BPM是等腰三角形时,如解图②,
可分三种情况进行讨论:
①当PM=MB,即PM2=MB2时,
y2-8y+17=y2+9,解得y1=1,
∴此时点M的坐标为(1,1);
第3题解图②
②当PM=PB,即PM2=PB2时,
y2-8y+17=20,
解得y2=4+ ,y3=4- ,
∴此时点M的坐标为(1,4+ )或(1,4- );
③当MB=PB,即MB2=PB2时,
y2+9=20,
解得y4= ,y5=- ,
∴此时点M的坐标为(1, )或(1,- ).
第3题解图②
综上所述,在PC的垂直平分线上存在一点M,使△BPM是等腰三角形,此时点M的坐标为(1,1)或(1,4+ )或(1,4- )或(1, )或(1,- ).
第3题解图②
(3)存在,点M的坐标为(1,1)或(1,4+ )
或(1,4- )或(1, )或(1,- ).
第4题图
4. 如图,抛物线与x轴交于B、C两点,与y轴交于A点,其中A、B、C三点构成直角三角形,∠BAC=90°,AB=2 ,AC=4 .
(1)求经过点A、B、C的抛物线的解析式;
解:(1)∵∠BAC=90°,AB=2 ,AC=4 ,
∴BC=10,
∵S△ABC= ×AB×AC= ×BC×AO,
即2 ×4 =10×AO,
∴AO=4,
则OC= =8,BO=2,
即B(-2,0),C(8,0),A(0,4),
设经过点A、B、C的抛物线的解析式为y=a(x+2)(x-8),
将A(0,4)代入得,4=a(0+2)(0-8),
解得a=- ,
故y=- (x+2)(x-8)=- x2+ x+4;
第4题图
(2)点P为x轴上方的抛物线上的一个动点,连接PA、PC,设所得△PAC的面积为S,求S等于多少时,相应的点P有且只有2个?
(2)设直线AC对应的函数解析式为y=kx+b(k≠0),
∴ ,解得 ,
∴直线AC对应的函数解析式为y=- x+4,
设P(m,- m2+ m+4),则Q(m,- m+4).
如解图①,过P作PH⊥OC,垂足为H,
交直线AC于点Q,连接PC、PA.
第4题图
H
P
Q
①当0<m<8时,
PQ= = ,
S=S△APQ+S△CPQ= ×8×(- m2+2m)=-(m-4)2+16,
∴0<S≤16;
②当-2≤m<0时,
PQ=(- m+4)-(- m2+ m+4)= m2-2m,
S=S△CPQ-S△APQ= ×8×( m2-2m)
=(m-4)2-16,
∴0<S<20;
第4题图
H
P
Q
∴当0<S<16时,0<m<8中有m两个值,-2≤m<0中m有一个值,此时有三个;
当16<S<20时,-2≤m<0中m只有一个值;
当S=16时,m=4或m=4-4 这两个.
故当S=16时,相应的点P有且只有两个;
第4题图
H
P
Q
(3)在直线AC上是否存在一点Q,使△QBC为等腰三角形?若存在,直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
【解法提示】如解图②所示.①当BQ=QC时,∵B(-2,0),C(8,0)
∴Q点横坐标为3,
则y=- ×3+4= ,
故此时Q点坐标为(3, );
②当BC=CQ1时,
设Q1(x,- x+4),
第4题解图②
过点Q1作Q1D⊥x轴于点D,
则DC=x-8,DQ1= x-4,
故DC2+Q1D2=Q1C2=BC2,
即(x-8)2+( x-4)2=100,
解得:x1=8+4 ,x2=8-4 ,
故y=-2 或2 ,
可得Q1(8+4 ,-2 ),
Q2(8-4 ,2 );
第4题解图②
③当BQ3=BC时,作Q3F⊥x轴于F,
同理可得:Q3F=- x+4,FB=-2-x,
故(-2-x)2+(- x+4)2=100,
解得:x1=8(不合题意舍去),x2=-8,
则y=8,
故Q3(-8,8),
综上所述,使△QBC为等腰三角形的所有符合条件的点Q的坐标分别为(3, ),(8+4 ,-2 ),(8-4 ,2 ),(-8,8).
第4题解图②
(3)存在,符合条件的点Q的坐标为(3, )或(8+4 ,-2 )或
(8-4 ,2 )或(-8,8).
第4题解图②
例1题图
微技能——分类讨论思想确定动点位置
一阶
一题多设问
例1 已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C.连接AC.
微专题:二次函数与等腰三角形问题
探究1:在抛物线对称轴上找一点P使得△ACP为等腰三角形.
(1)若AC为等腰三角形的底边时,AP=PC;在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例1题解图①
解:探究1:(1)满足条件的点P如解图①所示.
(2)若AC为等腰三角形的腰时,AC=________或AC=________;在图②中画出所有满足条件的点P的示意图(保留作图痕迹);
PC
AP
(2)满足条件的点P如解图②、③所示.
例1题解图②
例1题解图③
探究2:在抛物线上找一点E使得△BCE为等腰三角形.在图③中画出所有满足条件的点E的示意图(保留作图痕迹).
例1题图④
探究2:满足条件的点E如解图④、⑤所示.
例1题图⑤
【作图依据】______________________________________________
线段垂直平分线上的点到线段两端点的距离相等.
【方法总结】等腰三角形的存在性一般要分情况讨论:常以已知边为______或______讨论;以探究1为例,已知边AC为底时,可以作已知边的______________________,所找点即为__________________的交点;若已知边AC为腰时,作图方法为:_______________________________,所找点即为____________________
腰
底边
垂直平分线(中垂线)
垂直平分线和对称轴
圆与对称轴的交点.
AC的长为半径画圆
分别以点A、C为圆心,
三点共线时,不能构成三角形,须忽略.
●
易错警示
【思考】若动点在y轴上、x轴上时,确定动点位置有什么不同呢?
一题多设问
二阶
一题多设问
例2 如图①,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,顶点为M,对称轴与x轴交于点N.
例2题图①
(1)求抛物线的表达式及顶点M的坐标;
∴抛物线的表达式为y=- x2+ x+2
∴抛物线的对称轴为直线x= =
当x=1时,y=
∴顶点M的坐标为(1, );
解:(1)将点A(-1,0),B(3,0)代入抛物线y=- x2+bx+c中,
得 解得
例2题图①
例2题图②
(2)如图②,点P是抛物线上一点,当△PCO是以OC为底边的等腰三角形时,请直接写出点P的横坐标;
【思维教练】由于点P在抛物线上,△PCO是以OC为底边的等腰三角形,所以点P在OC的垂直平分线与抛物线的交点上.
例2题图②
令x=0,则y=2,∴C(0,2),∴OC=2,
∵△COP是以CO为底的等腰三角形,
∴CD=DO=1,
∴点P,P′的纵坐标为1,
当y=1时,- x2+ x+2=1,
P
P′
D
【解法提示】如解图①,作CO的垂直平分线交抛物线于点P和点P′,交CO于点D.连接CP、OP,OP′,CP′,△POC和△P′CO是以OC为底的等腰三角形.
解得x=1+ 或x=1- .
∴点P的横坐标为1+ ,
点P′的横坐标为1- .
即存在点P使△PCO是以OC为底边的等腰三角形,点P的横坐标为
1+ 或1- .
(2)点P的横坐标为1+ 或1-
例2题图②
P
P′
D
例2题图③
(3)如图③,点E是x轴上一点,当△ACE是等腰三角形时,请直接写出点E的坐标;
【思维教练】由于△ACE是等腰三角形,可分AC为底边,AC为腰两种情况分类讨论.
【解法提示】∵点E在x轴上,
∴设点E的坐标为(m,0).由(1)易得点C的坐标为(0,2),
∴AC= ,
∵△ACE是等腰三角形,
①当AE=AC时,
ⅰ.当点E在点A的右侧时,
∵AE=AC= ,
则EO= -1,
例2题图③
∴E的横坐标为 -1;
∴E( -1,0);
ⅱ.当点E在点A的左侧时,
∵AE=AC= ,则EO= +1,
∴点E的横坐标是- -1;
∴E(- -1,0);
②当AC=CE时,∵CO⊥AE,
∴点E在AO的延长线上,且AO=EO,
∴点E的横坐标为1;∴E(1,0);
例2题图③
③当AC为底时,则AE=CE时,则点E为AC的垂直平分线与x轴的交点.
∵AE=1+m,OE=m,
∴AE2=(1+m)2.
∵点C的坐标为(0,2),
∴OC=2.
∴CE2=m2+22.
∵CE=AE,∴22+m2=(1+m)2,
解得m=
例2题图③
∴E( ,0),
综上所述,点E的坐标为( -1,0)或(- -1,0)或(1,0)或
( ,0).
(3)点E的坐标为( -1,0)或(- -1,0)或(1,0)或( ,0);
例2题图③
例2题图④
(4)如图④,对称轴MN上一点是否存在点G,使得△CGB是等腰三角形,若存在,请直接写出点G的纵坐标;若不存在,请说明理由;
【思维教练】未明确说等腰三角形的腰和底,故要分类讨论:①CG=CB,②CG=BG,③BG=BC求解即可.
【解法提示】∵点G在对称轴上,∴设点G的坐标为(1,m),
∵点C(0,2),B(3,0),
∴BC2=22+32=13,CG2=1+(m-2)2,BG2=22+m2,
当△CGB是等腰三角形时,可分以下三种情况:
①当CG=CB时,1+(m-2)2=13,解得m=2+2 或m=2-2 ,
∴G(1,2+2 )或(1,2-2 );
②当CG=BG时,1+(m-2)2=22+m2,解得m= ,∴G(1, );
③当BG=BC时,22+m2=13,解得m=3或m=-3,
∴G(1,3)或(1,-3);
综上所述,当△CGB是等腰三角形时,点G的纵坐标为2+2 或
2-2 或 或3或-3.
(4)存在,点G的纵坐标为2+2 或2-2 或 或3或-3;
例2题图⑤
(5)如图⑤,点D的坐标为(4,0),动点Q从点A开始沿AC方向以每秒
个单位长度的速度运动,动点P从点C开始,沿CD方向以每秒 个单位长度的速度运动,当点Q到达终点时,两点同时停止运动.设运动时间为t,当△NPQ是等腰三角形时,请直接写出t的值.
【思维教练】根据题意用含t的式子表示出
QN,PQ,PN,由于不确定△NPQ的底和腰.
所以分下列三种情况讨论:
①NQ=NP,②NQ=PQ,③NP=PQ求解即可.
例2题图⑤
【解法提示】由点的坐标易得AC= ,CD=2 ,AD=5.
由勾股定理逆定理得AC2+CD2=AD2,∴∠ACD=90°.
根据题意可知,AQ= t,CP= t,∴CQ= - t,
∴PQ2=CQ2+CP2=( - t)2+( t)2= t2-5t+5,
Q
G
H
P
易得AG= t,QG=t,∴NG=2- t,
则NQ2=QG2+NG2= t2-2t+4,
同理可得NP2=5t2-8t+5,
其中t的取值范围是0≤t≤2.
如解图②,过点Q作QG⊥x轴于点G,过点P作PH⊥x轴于点H,
当△NPQ是等腰三角形时,则分以下几种情况:
①当NQ=NP时, t2-2t+4=5t2-8t+5,
整理得15t2-24t+4=0,解得t= 或t= ;
②当NQ=PQ时, t2-2t+4= t2-5t+5,
整理得5t2-3t+1=0,此方程无解,则此时t不存在;
例2题图⑤
Q
G
H
P
③当NP=PQ时,5t2-8t+5= t2-5t+5,
整理得5t2+12t=0,解得t=0或t=- (舍去).
综上所述,当△NPQ是等腰三角形时,t的值为 或 或0.
(5)t的值为 或 或0.
例2题图⑤
Q
G
H
P
综合训练
三阶
1.(2023抚顺新抚区一模)如图,直线y=- x+2与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A,B两点,P为x轴上的动点,P与A,O不重合,PC∥OB交抛物线于C,交直线AB于D,连接BC.
(1)求抛物线的解析式;
第1题图
备用图
解:(1)∵直线y=- x+2与x轴交于点A,与y轴交于点B,
当y=0时,x=4,
∴点A的坐标是(4,0),
当x=0时,y=2,
∴点B的坐标是(0,2),
又∵抛物线y=-x2+bx+c经过A,B两点,
∴ ,解得,
∴抛物线的解析式是y=-x2+ x+2;
第1题图
(2)当∠BCD=45°时,求点P的坐标;
(2)设点C的坐标是(x,y),当点C在第一象限时,
∵∠BCD=45°,
∴y-2=x,
∴y=-x2+ x+2=x+2,
∴x1= ,x2=0(不合题意,舍去),
∴点P的坐标是( ,0),
当点C在第四象限时,2-y=x,
∴y=-x2+ x+2=-x+2,
∴x1= ,x2=0(不合题意,舍去),
∴点P的坐标是 ( ,0),
综上所述,点P的坐标是( ,0)或( ,0);
第1题图
(3)当△BCD为等腰三角形时,直接写出点P的坐标.
E
则点E是等腰三角形△BCD的边DC中点,
则有yE= (yC+yD),
即2= (-m2+ m+2- m+2),
解得m1=3,m2=0(不合题意,舍去),
此时点P的坐标是(3,0);
【解法提示】设点P的坐标是(m,0),则点D的坐标是(m,- m+2),
当0<m<4时,若△BCD为等腰三角形时,则有以下情况:
①如解图①,当BC=BD时,过点B作BE⊥CD交CD于点E,
②当BC=CD时,
BC= , = =
CD=yC-yD=(-m2+ m+2)-(- m+2)=-m2+4m,
∵BC2=CD2,
∴m2(m2-7m+ )=m2(m2-8m+16),
解得m1= ,m2=0(不合题意,舍去),
∴此时点P的坐标是( ,0);
第1题图
E
第1题解图②
③当BD=CD时,
BD= = ,
CD=yC-yD=(-m2+ m+2)-(- m+2)=-m2+4m,
∴ m=-m2+4m,
解得m1= ,m2=0(不合题意,舍去),
∴此时点P的坐标是( ,0),
当m>4时,只有BD=CD,才能使△BCD为等腰三角形,如解图②,
则有CD=yD-yC=(- m+2)-(-m2+ m+2)=m2-4m,
解之得:m1= ,m2=0(舍去),
∴此时点P的坐标是( ,0);
综上所述,点P的坐标是(3,0)或( ,0)或( ,0)或P4( ,0).
(3)点P的坐标为(3,0)或( ,0)或( ,0)或( ,0).
∴ m=m2-4m,
第1题解图②
第2题图
2.如图,在平面直角坐标系中,抛物线y=ax2-x+c(a≠0)与x轴交于A(-1,0)、B(3,0)两点,直线AC与y轴交于点C,与抛物线交于点D,OA=OC.
(1)求该抛物线与直线AC的解析式;
备用图
解:(1)把A(-1,0)、B(3,0)代入y=ax2-x+c,得
解得
∴抛物线的解析式为y= x2-x- ;
∵OC=OA=1,
∴C(0,1),
设直线AC的解析式为y=kx+1(k≠0),则-k+1=0,解得k=1,
∴直线AC的解析式为y=x+1
设E(x, x2-x- )(-1<x<3),则G(x,x+1),
∴EG=x+1-( x2-x- )=- x2+2x+ .
∵OA=OC=1,∠AOC=90°,
∴∠OCA=45°,AC= = ,
第2题图
(2)若点E是x轴下方抛物线上一动点,连接AE、CE.求△ACE面积的最大值及此时点E的坐标;
(2)如解图①,作EG⊥x轴交直线AC于点G,作EH⊥AD于点H.
G
H
∵∠HGE=∠OCA=45°,
∴EH=EG·sin45°= (- x2+2x+ ),
第2题图
G
H
∴S△ACE= = =
∵ <0,且-1<2<3,
∴当x=2时,S△ACE最大= ,
此时E(2, ).
∴△ACE面积的最大值为 ,此时点E的坐标为(2, );
(3)将原抛物线沿射线AD方向平移2 个单位长度,得到新抛物线:y1=a1x2+b1x+c1(a≠0),新抛物线与原抛物线交于点F,在直线AD上是否存在点P,使以点P、D、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
第2题图
备用图
第2题解图②
【解法提示】如解图②,在直线AC上取一点A′,使它的横坐标为1,则A′(1,2),AA′= = ,
∴点A′即为抛物线平移后点A的对应点,
可知抛物线向右、向上各平移2个单位长度.
∵
∴平移后的抛物线为 ,其顶点坐标为(3,0);
∵原抛物线与新抛物线都经过点B(3,0),
∴点B即为新抛物线与原抛物线的交点F.
作A′K⊥x轴于点K,则∠AKA′=∠FKA′=90°,AK=A′K=FK=2,
∴∠AA′K=∠FA′K=45°,
∴∠AA′F=90°.
由 ,解得 或 (不符合题意,舍去)
∴D(5,6),
∴FD= .
①当FP1=FD时,则点P1与点D关于点A′对称,
∴P1(-3,-2);
②当P2D=FD= 时,
∵CD= ×5=5 ,
∴CP2= - ,
∴xp= ,yp= ,
P2( , );
第2题解图②
③当DP3=FP3时,
∵∠P3DF=∠FDP1,∠DFP3=∠DP1F,
∴△P3DF∽△FDP1,∴ ,
∵DP1= ×(5+3)=8 ,
∴ ,
∴CP3= ,
∴xp= ,yp= ,∴P3( , );
第2题解图②
④当P4D=FD=2 时,则CP4= ,
∴xp= ,
yp= ,
∴P4( , ).
综上所述,点P的坐标为(-3,-2)或( , )或( , )或( , ).
(3)存在,点P的坐标为(-3,-2)或( , )或( , )或
( , ).
第3题图
3.如图,抛物线y=ax2+x+c与x轴交于A,B(4,0)两点(点A在点B的左侧),与y轴交于点C(0,4),直线BC经过B,C两点,点P是第一象限内抛物线上的一个动点,连接PB,PC.
(1)求抛物线的函数表达式;
解:(1)由题意,将B(4,0),C(0,4)代入抛物线
y=ax2+x+c,得 解得
∴抛物线的函数表达式为y=- x2+x+4;
第3题图
第3题图
(2)设点P的横坐标为n,四边形OBPC的面积为S,求S的最大值并求出此时点P的坐标;
(2)如解图①,过点P作PE⊥x轴于点E,交BC于点F.
∵B(4,0),C(0,4),
∴OB=OC=4.
易得直线BC的表达式为y=-x+4.
∵点P的横坐标为n,
∴P(n,- n2+n+4),F(n,-n+4).
∴PF=- n2+n+4-(-n+4)=- n2+2n,
E
F
∴S四边形OBPC=S△BOC+S△PBF+S△PCF= = =
= ×4×4+ ×( n2+2n)×4=-n2+4n+8=-(n-2)2+12
∵-1<0,0<n<4.
∴当n=2时,S有最大值,S最大=12,
此时- n2+n+4=- ×22+2+4=4,
∴此时点P的坐标为(2,4);
第3题图
E
F
第3题图
(3)在(2)的条件下,当S取最大值时,在PC的垂直平分线上是否存在一点M,使△BPM是等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【解法提示】∵P(2,4),C(0,4),
∴PC∥x轴,PC=2,
∴PC的垂直平分线⊥x轴且为直线x=1,
∴点M的横坐标为1,
∴可设点M的坐标为(1,y).
又∵B(4,0),P(2,4),
∴PM2=(1-2)2+(y-4)2=y2-8y+17,
MB2=(1-4)2+y2=y2+9,
PB2=(4-2)2+(0-4)2=20.
当△BPM是等腰三角形时,如解图②,
可分三种情况进行讨论:
①当PM=MB,即PM2=MB2时,
y2-8y+17=y2+9,解得y1=1,
∴此时点M的坐标为(1,1);
第3题解图②
②当PM=PB,即PM2=PB2时,
y2-8y+17=20,
解得y2=4+ ,y3=4- ,
∴此时点M的坐标为(1,4+ )或(1,4- );
③当MB=PB,即MB2=PB2时,
y2+9=20,
解得y4= ,y5=- ,
∴此时点M的坐标为(1, )或(1,- ).
第3题解图②
综上所述,在PC的垂直平分线上存在一点M,使△BPM是等腰三角形,此时点M的坐标为(1,1)或(1,4+ )或(1,4- )或(1, )或(1,- ).
第3题解图②
(3)存在,点M的坐标为(1,1)或(1,4+ )
或(1,4- )或(1, )或(1,- ).
第4题图
4. 如图,抛物线与x轴交于B、C两点,与y轴交于A点,其中A、B、C三点构成直角三角形,∠BAC=90°,AB=2 ,AC=4 .
(1)求经过点A、B、C的抛物线的解析式;
解:(1)∵∠BAC=90°,AB=2 ,AC=4 ,
∴BC=10,
∵S△ABC= ×AB×AC= ×BC×AO,
即2 ×4 =10×AO,
∴AO=4,
则OC= =8,BO=2,
即B(-2,0),C(8,0),A(0,4),
设经过点A、B、C的抛物线的解析式为y=a(x+2)(x-8),
将A(0,4)代入得,4=a(0+2)(0-8),
解得a=- ,
故y=- (x+2)(x-8)=- x2+ x+4;
第4题图
(2)点P为x轴上方的抛物线上的一个动点,连接PA、PC,设所得△PAC的面积为S,求S等于多少时,相应的点P有且只有2个?
(2)设直线AC对应的函数解析式为y=kx+b(k≠0),
∴ ,解得 ,
∴直线AC对应的函数解析式为y=- x+4,
设P(m,- m2+ m+4),则Q(m,- m+4).
如解图①,过P作PH⊥OC,垂足为H,
交直线AC于点Q,连接PC、PA.
第4题图
H
P
Q
①当0<m<8时,
PQ= = ,
S=S△APQ+S△CPQ= ×8×(- m2+2m)=-(m-4)2+16,
∴0<S≤16;
②当-2≤m<0时,
PQ=(- m+4)-(- m2+ m+4)= m2-2m,
S=S△CPQ-S△APQ= ×8×( m2-2m)
=(m-4)2-16,
∴0<S<20;
第4题图
H
P
Q
∴当0<S<16时,0<m<8中有m两个值,-2≤m<0中m有一个值,此时有三个;
当16<S<20时,-2≤m<0中m只有一个值;
当S=16时,m=4或m=4-4 这两个.
故当S=16时,相应的点P有且只有两个;
第4题图
H
P
Q
(3)在直线AC上是否存在一点Q,使△QBC为等腰三角形?若存在,直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
【解法提示】如解图②所示.①当BQ=QC时,∵B(-2,0),C(8,0)
∴Q点横坐标为3,
则y=- ×3+4= ,
故此时Q点坐标为(3, );
②当BC=CQ1时,
设Q1(x,- x+4),
第4题解图②
过点Q1作Q1D⊥x轴于点D,
则DC=x-8,DQ1= x-4,
故DC2+Q1D2=Q1C2=BC2,
即(x-8)2+( x-4)2=100,
解得:x1=8+4 ,x2=8-4 ,
故y=-2 或2 ,
可得Q1(8+4 ,-2 ),
Q2(8-4 ,2 );
第4题解图②
③当BQ3=BC时,作Q3F⊥x轴于F,
同理可得:Q3F=- x+4,FB=-2-x,
故(-2-x)2+(- x+4)2=100,
解得:x1=8(不合题意舍去),x2=-8,
则y=8,
故Q3(-8,8),
综上所述,使△QBC为等腰三角形的所有符合条件的点Q的坐标分别为(3, ),(8+4 ,-2 ),(8-4 ,2 ),(-8,8).
第4题解图②
(3)存在,符合条件的点Q的坐标为(3, )或(8+4 ,-2 )或
(8-4 ,2 )或(-8,8).
第4题解图②
同课章节目录
