【七下专项突破讲练】专题10.14 用二元一次方程组解决问题(2)(分层练习)(基础练)(含解析)
文档属性
| 名称 | 【七下专项突破讲练】专题10.14 用二元一次方程组解决问题(2)(分层练习)(基础练)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 604.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 07:02:47 | ||
图片预览


文档简介
专题10.14 用二元一次方程组解决问题(2)(分层练习)(基础练)
一、选择题
【考点1】数字问题;
1.已知某首歌曲的歌词的字数是一个两位数,十位数字是个位数字的两倍,且十位数字比个位数字大4,则这首歌的歌词的字数是( )
A.84 B.48 C.41 D.148
2.一个两位数的两个数字之和为10,两个数字之差为6,求这个两位数,此题的解有( )
A.0个 B.1个 C.2个 D.4个
【考点2】年龄问题;
3.学生问老师:“您今年多大了”老师风趣地说:“我像你这么大的时候,你才出生,你到我这么大时,我已经36岁了,”那么老师和学生的年龄分别是( )
A.24、12 B.24、11 C.25、11 D.26、10
4.甲是乙现在的年龄时,乙8岁;乙是甲现在年龄时,甲20岁,则( )
A.甲比乙大6岁 B.乙比甲大6岁
C.甲比乙大4岁 D.乙比甲大4岁
【考点3】销售、利润问题;
5.某学校为了打造“书香校园”,丰富师生的业余文化生活,计划采购,两种图书,已知采购2本种图书和3本种图书共需110元,采购1本种图书和5本种图书共需160元,则,两种图书的单价分别为( )
A.10元、30元 B.30元、10元 C.25元、20元 D.60元、20元
6.春节前夕,某旅游景区的成人票和学生票均打折,李凯同学一家(个成人和个学生)去了该景区,门票共花费元,王玲同学一家(个成人和个学生)去了该景区,门票共花费元,则赵芸同学和妈妈去该景区游玩时,门票需要花费( )
A.元 B.元 C.元 D.元
【考点4】图表信息问题;
7.在“幻方拓展课程”探索中,小明在如图的方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则( )
6
0
A.2 B.4 C. D.6
8.某同学去蛋糕店买面包,面包有A,B两种包装,每个面包品质相同,且只能整盒购买,商品信息如下:
A包装盒 B包装盒
每盒面包个数(个) 3 8
每盒价格(元) 5 11
若某同学正好买了50个面包,则他最少需要花( )元;
A.71 B.74 C.75 D.81
【考点5】古代问题;
9.我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有16头,下有44足,问鸡兔各几何.”设鸡x只,兔y只,可列方程组( )
A. B.
C. D.
10.《孙子算经》中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,木长多少尺?若设绳子长x尺,木长y尺,所列方程组正确的是( )
A. B.
C. D.
【考点6】几何图形问题.
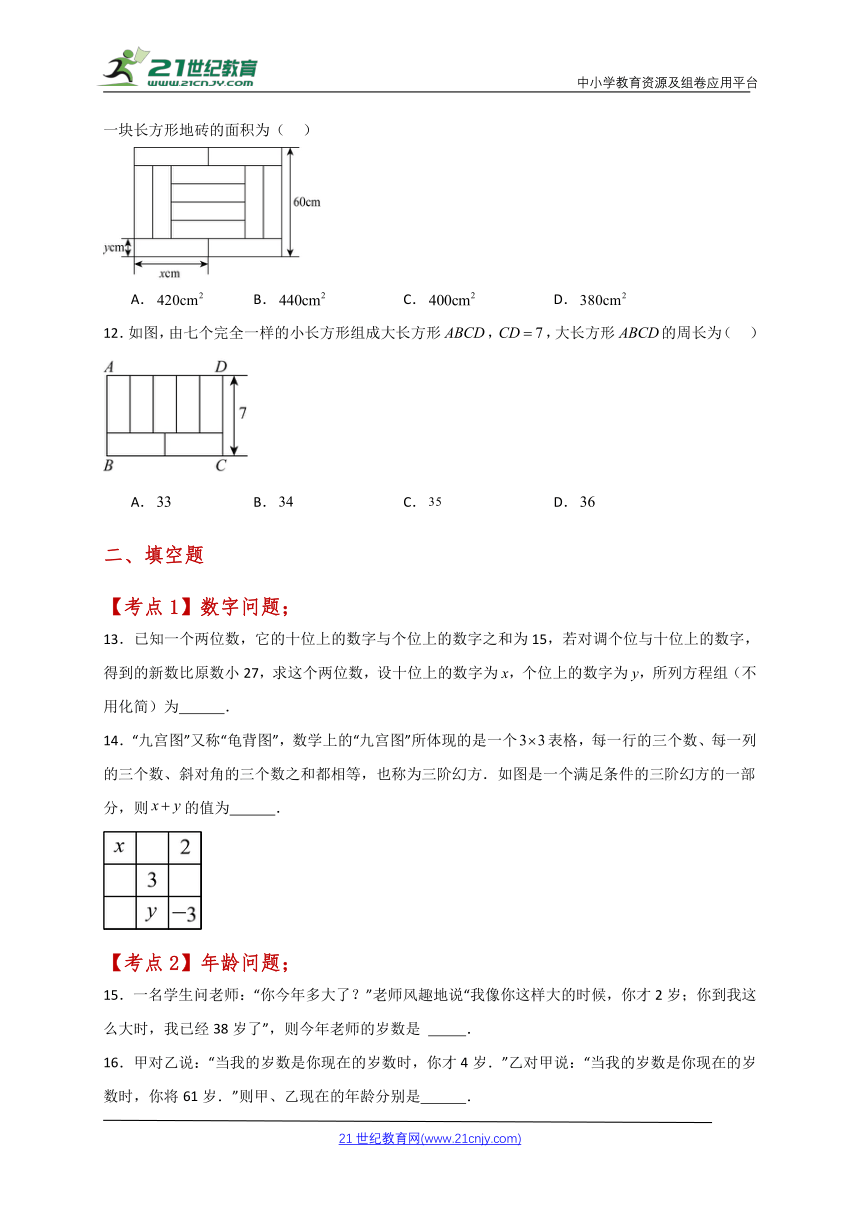
11.如图,用12块相同的长方形地砖拼成一个长方形.设一块长方形地砖的长和宽分别为和,一块长方形地砖的面积为( )
A. B. C. D.
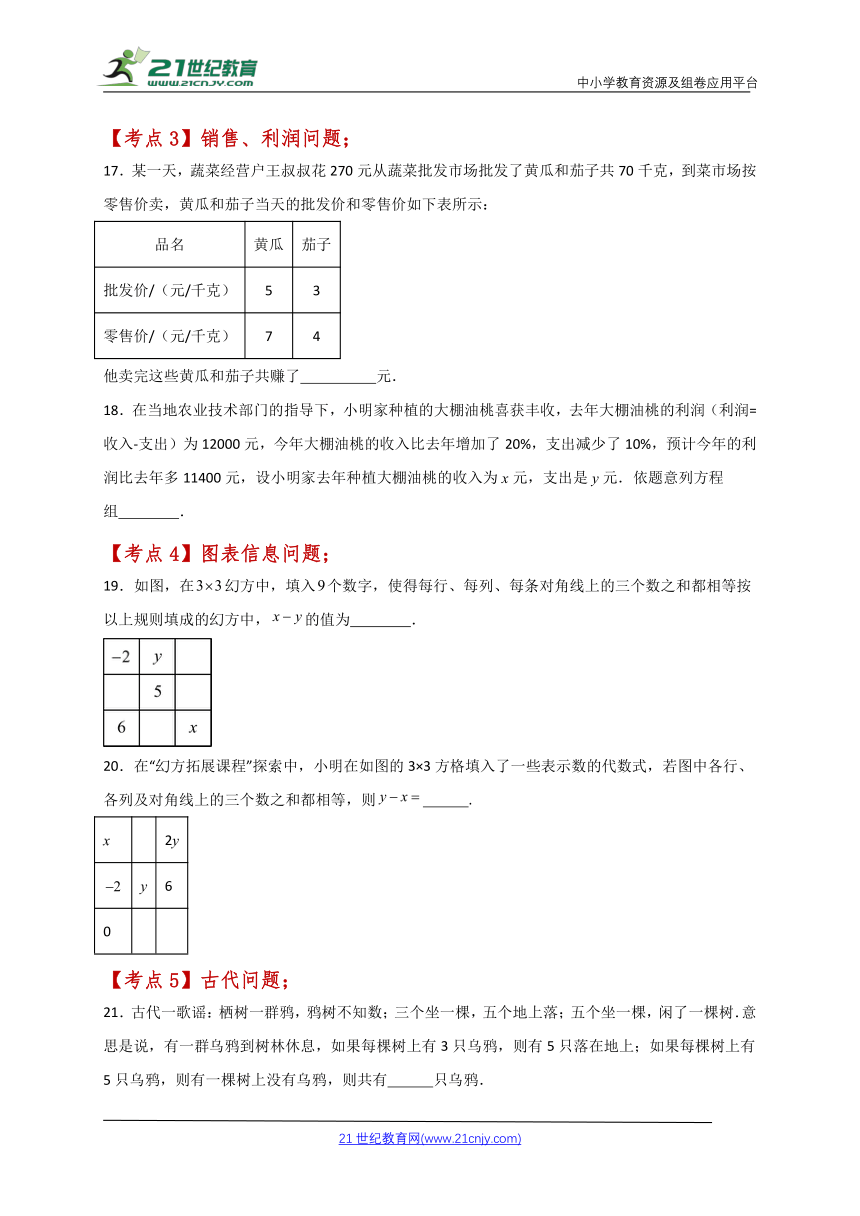
12.如图,由七个完全一样的小长方形组成大长方形,,大长方形的周长为( )
A. B. C. D.
二、填空题
【考点1】数字问题;
13.已知一个两位数,它的十位上的数字与个位上的数字之和为15,若对调个位与十位上的数字,得到的新数比原数小27,求这个两位数,设十位上的数字为x,个位上的数字为y,所列方程组(不用化简)为 .
14.“九宫图”又称“龟背图”,数学上的“九宫图”所体现的是一个表格,每一行的三个数、每一列的三个数、斜对角的三个数之和都相等,也称为三阶幻方.如图是一个满足条件的三阶幻方的一部分,则的值为 .
【考点2】年龄问题;
15.一名学生问老师:“你今年多大了?”老师风趣地说“我像你这样大的时候,你才2岁;你到我这么大时,我已经38岁了”,则今年老师的岁数是 .
16.甲对乙说:“当我的岁数是你现在的岁数时,你才4岁.”乙对甲说:“当我的岁数是你现在的岁数时,你将61岁.”则甲、乙现在的年龄分别是 .
【考点3】销售、利润问题;
17.某一天,蔬菜经营户王叔叔花270元从蔬菜批发市场批发了黄瓜和茄子共70千克,到菜市场按零售价卖,黄瓜和茄子当天的批发价和零售价如下表所示:
品名 黄瓜 茄子
批发价/(元/千克) 5 3
零售价/(元/千克) 7 4
他卖完这些黄瓜和茄子共赚了 元.
18.在当地农业技术部门的指导下,小明家种植的大棚油桃喜获丰收,去年大棚油桃的利润(利润=收入-支出)为12000元,今年大棚油桃的收入比去年增加了20%,支出减少了10%,预计今年的利润比去年多11400元,设小明家去年种植大棚油桃的收入为x元,支出是y元.依题意列方程组 .
【考点4】图表信息问题;
19.如图,在幻方中,填入个数字,使得每行、每列、每条对角线上的三个数之和都相等按以上规则填成的幻方中,的值为 .
20.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则 .
x 2y
y 6
0
【考点5】古代问题;
21.古代一歌谣:栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思是说,有一群乌鸦到树林休息,如果每棵树上有3只乌鸦,则有5只落在地上;如果每棵树上有5只乌鸦,则有一棵树上没有乌鸦,则共有 只乌鸦.
22.在《九章算术》中,一次方程组是由算筹布置而成的.图1所示的算筹图表示的是关于,的方程组,则图2所示的算筹图表示的方程组是 .
【考点6】几何图形问题.
23.如图,两根铁棒直立于桶底在水平面的木桶中,在桶中加入水后,一根露出水面的长度是它总长的,另一根露出水面的长度是它总长的.两根铁棒长度之和为,则两根铁棒的长度分别为 .
24.如图,长方形中放置9个形状,大小完全相同的小长方形,根据图中数据,求出图中阴影面积为 .
三、解答题
【考点1】数字问题;
25.一个两位数,十位上的数与个位上的数之和是8,个位数字与十位数字交换后所得新数比原数大.求这个两位数.
26.根据下列语句,分别设适当的未知数,列二元一次方程或方程组.
(1)甲数的比乙数的5倍大2;
(2)梯形的面积为,高是6cm,且下底比上底的2倍少1cm,求梯形上底和下底的长;
(3)如图,点C在直线上,的度数比的度数的3倍少,求和的度数.
【考点2】年龄问题;
27.5年前母亲的年龄是女儿年龄的15倍,15年后,母亲的年龄比女儿年龄的2倍多6岁.那么现在这对母女的年龄分别是多少?
28.10年前,小明妈妈的年龄是小明的6倍;10年后,小明妈妈的年龄将是小明的2倍.小明和他妈妈现在的年龄分别是多少?
【考点3】销售、利润问题;
29.某百货大楼购进商品后,加价作为销售价.五一黄金周快到了,商场搞优惠促销活动,决定A、B两种商品分别以折和折销售,某顾客购买A、B两种商品,共付款元.这两种商品原销售价之和为元,问这两种商品实际销售价格分别为多少元?
30.某海鲜排档购进一批大龙虾和海胆,它们的进货单价之和是360元.大龙虾零售单价比进货单价多40元,海胆零售单价比进货单价的1.5倍少60元,按零售单价购买大龙虾2只和海胆4个,共需要1200元.
(1)求大龙虾和海胆的进货单价;
(2)该海鲜排档平均每天卖出大龙虾20只和海胆12个.经调查发现,大龙虾零售单价每降低1元,平均每天就可多售出大龙虾2只,海鲜排档决定把大龙虾的零售单价下降元,海胆的零售单价和销量都不变,在不考虑其他因素的条件下,当a为多少时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元?
【考点4】图表信息问题;
31.某学校现有甲种材料,乙种材料,制作A,B两种型号的工艺品,用料情况如下表:
需甲种材料 需乙种材料
1件A型工艺品
1件B型工艺品
(1)利用这些材料能制作A,B两种型号的工艺品各多少件?
(2)若每千克甲、乙两种材料分别为8元和10元,问:制作A,B两种型号的工艺品各需材料费多少钱?
32.某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:若商场购进甲、乙两种型号的电视机共50台,用去9万元.
电视机型号 甲 乙
批发价(元/台) 1500 2500
零售价批发价(元/台) 2025 3640
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“国庆”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利,求甲种型号电视机打几折销售?
【考点5】古代问题;
33.《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣.其中下卷“雉兔同笼”流传尤为广泛.“雉兔同笼”题为:今有雉(鸡)兔同笼,上有三十五头,下有九十四足,问雉兔各几何?上述“雉兔同笼”问题中,鸡和兔各有多少只?
34.《九章算术》中记载:“今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?”意思是:今有人合伙买金,每人出钱400,会多出3400钱;每人出钱300,会多出100钱,问合伙人数、金价各是多少?
【考点6】几何图形问题.
35.列二元一次方程组解应用题:某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?
36.如图,这是某江滩公园正在修建的一运动场馆的规划示意图,运动场馆是一个长方形,长为120米,宽为90米,计划在甲、乙、丙三块形状及大小相同的小长方形地块上修建网球场,剩余两块形状及大小相同的空地铺设塑胶草坪,求每块草坪的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】设这首歌的歌词的字数的十位数字为x,个位数字为y,由题意:十位数字是个位数字的两倍,且十位数字比个位数字大4,列出二元一次方程组,解方程组即可.
【详解】解:设这个两位数的个位数是x,十位数是y.
根据题意,得
解得
则这首歌的歌词的字数是84个.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
2.C
【分析】设这个两位数为,依题意,则或,解方程组即可求解.
【详解】解:设这个两位数为,依题意,则或,
解得:或,
故选:C.
【点睛】本题考查了二元一次方程组的应用,根据题意列出方程组是解题的关键.
3.A
【分析】设老师现在的年龄是岁,学生现在的年龄是岁,抓住年龄差不变,根据此等量关系可列方程组求解.
【详解】解:设老师现在的年龄是岁,学生现在的年龄是岁,
由题意可得:,
解得:.
故老师现在的年龄是24岁,学生现在的年龄是12岁.
故选:A.
【点睛】本题考查了二元一次方程组的应用,关键是知道年龄差是不变的量从而可列方程求解.
4.C
【分析】根据题中已知量和未知量之间的等量关系,设未知数,列二元一次方程组即可解决.
【详解】解:设甲现在x岁,乙现在y岁.
根据题意,得,
解得,
∴
故选:C
【点睛】本题考查了列方程组解应用题的知识点,找出题中已知量和未知之间的等量关系是解题的关键.
5.A
【分析】
本题考查了二元一次方程组的应用,设,两种图书的单价分别为元,元,根据题意列出方程组,解方程组即可求解.
【详解】解:设,两种图书的单价分别为元,元,根据题意得,
解得:
即,两种图书的单价分别为10元、30元,
故选:A.
6.A
【分析】设成人票是元张,学生票是元张,根据“李凯同学一家个成人和个学生去了该景区,门票共花费元,王玲同学一家个成人和个学生去了该景区,门票共花费元”列出方程组,求得的值即可.
【详解】解:设成人票是元张,学生票是元张,
依题意得:
,
②①得:.
即赵芸同学和妈妈去该景区游玩时,门票需要花费元.
故选:A.
【点睛】本题考查了二元一次方程组的应用.此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为,另一个未知数用含的式子来表示,进而列并解方程即可.
7.C
【分析】本题考查了二元一次方程组的应用及求代数式的值,能根据题意列出方程组是解此题的关键.根据题意得出方程组,求出方程组的解,代入计算即可.
【详解】解:由题意得:,
解得:,
∴.
故选:C.
8.B
【分析】设购买A包装面包x盒,B包装面包y盒,由题意:某同学正好买了50个面包,结合表中信息列出二元一次方程,求出非负整数解,即可解决问题.
【详解】解:设购买A包装面包x盒,B包装面包y盒,
由题意得: 3x + 8y= 50,
∵x、y为非负整数
∴ 或 ,
∴当x=6,y= 8时,
费用为:5×6+11×4= 74(元);
当x= 14,y= 1时,费用为:5×14+11×1= 81(元);
∵74<81,
∴某同学正好买了50个面包,则他最少需要花74元
故选: B.
【点睛】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
9.A
【分析】本题考查了由实际问题抽象出二元一次方程组,解题的关键是找出等量关系.
设鸡x只,兔y只,根据上有16头,下有44足列出二元一次方程组即可.
【详解】设鸡x只,兔y只,
根据题意得,.
故选:A.
10.B
【分析】此题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程组是解答本题的关键.根据“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量木条,木头剩余1尺”,即可得出方程组即可.
【详解】解:∵用绳子去量长木,绳子还剩余4.5尺,
∴;
∵将绳子对折再量长木,长木还剩余1尺,
∴.
∴所列方程组为.
故选:B.
11.C
【分析】
本题主要考查了二元一次方程组的实际应用,设一块长方形地砖的长和宽分别为和,根据题意可知宽的两倍与长的和为,2个长与4个宽加一个长的长度相等,据此列出方程组求解即可.
【详解】解:由题意得,,
解得,
∴一块长方形地砖的面积为,
故选:C.
12.B
【分析】此题考查二元一次方程组的应用,正确的理解题意是解题的关键. 由图可看出本题的等量关系:小长方形的长小长方形的宽;小长方形的长+宽,据此可以列出方程组求解.
【详解】解:设小长方形的长为x,宽为y.
由图可知,
解得.
所以长方形的长为10,宽为7,
∴长方形的周长为,
故选B.
13.
【分析】本题考查二元一次方程组的应用,由“十位上的数字与个位上的数字之和为15”可得,这个两位数表示为,对调个位与十位上的数字表示为,根据“得到的新数比原数小27”可得方程“”,组成方程组即可.
【详解】解:根据“它的十位上的数字与个位上的数字之和为15,若对调个位与十位上的数字,得到的新数比原数小27”,
可得:
故答案为:.
14.17
【分析】根据三阶幻方的规则列出方程组求解x、y即可.
【详解】解:由题意,得,
解得,
∴,
故答案为:17.
【点睛】本题考查二元一次方程组的应用,理解题意,找出等量关系,正确列出方程组是解答的关键.
15.26
【分析】设今年老师的岁数是x岁,学生的岁数是y岁,根据学生今年年龄减年龄差等于2,老师今年年龄加年龄差等于38,列出二元一次方程组即可.
【详解】解:设今年老师的岁数是x岁,学生的岁数是y岁,
依题意得:,
解得:.
故答案为:26.
【点睛】本题考查二元一次方程组,设出恰当的未知数,准确抓住数量关系列出方程组是解题的关键.
16.42岁,23岁
【分析】设甲现在x岁,乙现在y岁,根据甲、乙年龄之间的关系,可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设甲现在x岁,乙现在y岁,
依题意,得:,
解得:.
答:甲现在42岁,乙现在23岁.
故答案为:42岁,23岁.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
17.100
【分析】
本题考查二元一次方程组的实际应用,设批发黄瓜千克,茄子千克,根据王叔叔花270元从蔬菜批发市场批发了黄瓜和茄子共70千克,列出方程组求出的值,再利用总利润等于单件利润乘以销量,求解即可.
【详解】解:设批发黄瓜千克,茄子千克,由题意,得:
,解得:,
∴(元);
故答案为:100.
18.
【分析】审题,明确等量关系,建立方程组.
【详解】解:由题意知,今年收入为,今年支出,故
故答案为:
【点睛】本题考查二元一次方程组的应用,根据题意明确等量关系是解题的关键.
19.
【分析】根据题意可知每行每列每对角线上的三个数之和都相等可知,即可得解;
【详解】∵每行每列每对角线上的三个数之和都相等,
∴,
解得,
故答案为:.
【点睛】本题考查了有理数的加法,二元一次方程的应用,根据表格,根据每行每列每对角线上的三个数之和都相等得知是解题的关键.
20.
【分析】根据图中各行、各列上的三个数之和都相等,即可得出关于x,y的二元一次方程组,求解后即可得出结果.
【详解】解:依题意得: ,
解得,
∴.
故答案为:.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
21.
【分析】本题考查二元一次方程组与实际问题.根据题意可设乌鸦有只,树有棵,然后列出方程组求解即可.
【详解】解:设乌鸦有只,树有棵,依题得
解得
故答案为:.
22.
【分析】
本题考查了由实际问题抽象出二元一次方程组以及数学常识,找准等量关系,正确列出二元一次方程组是解题的关键.
根据图1所表示方程组,可找出各算筹表示的数量:第一列表示x系数,第二列表示y系数,第三列表示常数项,进而可得出图2所表示的方程组
【详解】解:由题意,图2所示的算筹图表示的方程组是,
故答案为:.
23.,
【分析】本题主要考查了二元一次方程组的应用,解题的关键是设两根铁棒的长度分别为,,根据两根铁棒长度之和为,一根露出水面的长度是它总长的,另一根露出水面的长度是它总长的,列出方程组,解方程组即可.
【详解】解:设两根铁棒的长度分别为,,由题意得:
解得:,
故答案为:,.
24.18
【分析】本题考查了二元一次方程组的应用,设每个小长方形的长为x,宽为y,根据题意,得,结合计算即可.
【详解】设每个小长方形的长为x,宽为y,根据题意,得
,
解得
故,
故答案为:18.
25.这个两位数为
【分析】
本题考查了二元一次方程组的应用,设这个两位数的十位数字为x,个位数字为y.可列方程组求解.
【详解】解:设这个两位数的十位数字为x,个位数字为y.
依题意,得:
解得:
答:这个两位数为.
26.(1)
(2)
(3)
【详解】(1)设甲数为x,乙数为y,则.
(2)设梯形的上底为xcm,下底为ycm,则
(3)设和的度数分别为,,则
27.母亲现在年龄35岁,女儿现在7岁
【分析】设母亲现在年龄x岁,女儿现在y岁,然后根据5年前母亲的年龄是女儿年龄的15倍,15年后,母亲的年龄比女儿年龄的2倍多6岁,列出方程组求解即可.
【详解】解:设母亲现在年龄x岁,女儿现在y岁,则
解得
答:母亲现在年龄35岁,女儿现在7岁.
【点睛】本题主要考查了二元一次方程组的应用,解题的关键在于正确理解题意列出方程求解.
28.小明和他妈妈现在的年龄分别是15岁和40岁
【分析】根据题意,设小明和他妈妈现在的年龄分别是x岁和y岁,列二元一次方程组,解方程求解即可
【详解】设小明和他妈妈现在的年龄分别是x岁和y岁,根据题意,
得
解得
答:小明和他妈妈现在的年龄分别是15岁和40岁.
【点睛】本题考查了二元一次方程组的应用,根据题意列出方程组是解题的关键.
29.这两种商品实际销售价格分别为、元.
【分析】本题考查了二元一次方程组的应用,读懂题意,找出数量关系是解题关键.设这两种商品实际销售价格分别为、元,根据题意列二元一次方程组求解即可.
【详解】解:设这两种商品实际销售价格分别为、元,
由题意得:,
解得:,
答:这两种商品实际销售价格分别为、元.
30.(1)大龙虾进货单价为200元,海胆的进货单价为160元
(2)15
【分析】本题考查了一元二次方程的应用∶
(1)设大龙虾进货单价为x元,海胆的进货单价为y元,由它们的进货单价之和是360元和按零售单价购买大龙虾2只和海胆4个,共需要1200元,列出方程组,即可求解;
(2)由海鲜排档每天销售大龙虾和海胆获取的总利润为1490元,列出方程可求解.
【详解】(1)解:设大龙虾进货单价为x元,海胆的进货单价为y元,依题意有∶
,
解得:,
答:大龙虾进货单价为200元,海胆的进货单价为160元;
(2)依题意有,
解得.
故当a为15时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元.
31.(1)制作A种型号的工艺品30件,B种型号的工艺品20件
(2)306元,264元
【分析】
本题主要考查了二元一次方程组的应用,另外还涉及有理数混合运算的应用;
(1)设利用这些材料能制作A种型号的工艺品x件,B种型号的工艺品y件,根据等量关系:两种工艺品所需甲种材料为,两种工艺品所需乙种材料为,列出二元一次方程组,并求解即可;
(2)分别计算出制作1件两种型号的工艺品需要的费用,则可计算出制作A,B两种型号的工艺品各需材料费.
【详解】(1)解:设利用这些材料能制作A种型号的工艺品x件,B种型号的工艺品y件,
由题意,得,解得;
答:利用这些材料能制作A种型号的工艺品30件,B种型号的工艺品20件.
(2)解:制作1件A种型号的工艺品需要(元),
则制作A种型号的工艺品需材料费(元);
制作1件B种型号的工艺品需要(元),
则制作B种型号的工艺品需材料费(元).
答:制作A,B两种型号的工艺品各需材料费306元,264元.
32.(1)购进甲型号电视机35台,乙型号电视机15台
(2)8折
【分析】(1)设商场购进甲型号电视机台,乙型号电视机台,根据“商场购进甲、乙两种型号的电视机共50台,用去9万元”列出二元一次方程组,解方程组即可;
(2)设甲种型号电视机打折销售,根据“两种电视机销售完毕,商场共获利”列出一元一次方程,解方程即可.
【详解】(1)解:设商场购进甲型号电视机台,乙型号电视机台,
由题意得:,
解得:,
答:商场购进甲型号电视机35台,乙型号电视机15台;
(2)设甲种型号电视机打折销售,
由题意得:,
解得:,
答:甲种型号电视机打8折销售.
【点睛】本题考查了二元一次方程组和一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元一次方程.
33.鸡和兔各有23只,12只
【分析】本题主要考查了二元一次方程组的实际应用,设鸡有x只,兔有y只,根据共有三十五头可得方程,根据共有九十四足,可得方程,据此列出方程组求解即可.
【详解】解:设鸡有x只,兔有y只,
由题意得,,
解得,
答:鸡和兔各有23只,12只.
34.合伙人数是33人,金价是9800钱
【分析】
本题考查了二元一次方程组的应用以及数学常识.设共人合伙买金,金价为钱,根据“每人出400钱,会剩余3400钱;每人出300钱,会剩余100钱”,即可得出关于,的二元一次方程组,解之即可得出结论.
【详解】
解:设共人合伙买金,金价为钱,
依题意得:,
解得:.
答:共33人合伙买金,金价为9800钱.
35.预计花费75600元.
【分析】本题考查的是二元一次方程组的应用,根据长方形的性质列出方程组是解本题的关键.
设小长方形的长为米,宽为米,则根据长方形的性质可列方程组,再解方程组即可得到答案.
【详解】解:设小长方形的长为米,宽为米,
依题意得
解得
所以(元).
答:预计花费75600元.
36.3900平方米
【分析】本题考查了二元一次方程组的应用.三个小长方形的长为x米,宽为y米,根据题意,列出方程,可求出三个小长方形的总面积,再用大长方形的面积减去三个小长方形的总面积,即可求解.
【详解】解:设三个小长方形的长为x米,宽为y米,根据题意得:
,
解得:,
∴三个小长方形的总面积为平方米,
∴每块草坪的面积为平方米.
一、选择题
【考点1】数字问题;
1.已知某首歌曲的歌词的字数是一个两位数,十位数字是个位数字的两倍,且十位数字比个位数字大4,则这首歌的歌词的字数是( )
A.84 B.48 C.41 D.148
2.一个两位数的两个数字之和为10,两个数字之差为6,求这个两位数,此题的解有( )
A.0个 B.1个 C.2个 D.4个
【考点2】年龄问题;
3.学生问老师:“您今年多大了”老师风趣地说:“我像你这么大的时候,你才出生,你到我这么大时,我已经36岁了,”那么老师和学生的年龄分别是( )
A.24、12 B.24、11 C.25、11 D.26、10
4.甲是乙现在的年龄时,乙8岁;乙是甲现在年龄时,甲20岁,则( )
A.甲比乙大6岁 B.乙比甲大6岁
C.甲比乙大4岁 D.乙比甲大4岁
【考点3】销售、利润问题;
5.某学校为了打造“书香校园”,丰富师生的业余文化生活,计划采购,两种图书,已知采购2本种图书和3本种图书共需110元,采购1本种图书和5本种图书共需160元,则,两种图书的单价分别为( )
A.10元、30元 B.30元、10元 C.25元、20元 D.60元、20元
6.春节前夕,某旅游景区的成人票和学生票均打折,李凯同学一家(个成人和个学生)去了该景区,门票共花费元,王玲同学一家(个成人和个学生)去了该景区,门票共花费元,则赵芸同学和妈妈去该景区游玩时,门票需要花费( )
A.元 B.元 C.元 D.元
【考点4】图表信息问题;
7.在“幻方拓展课程”探索中,小明在如图的方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则( )
6
0
A.2 B.4 C. D.6
8.某同学去蛋糕店买面包,面包有A,B两种包装,每个面包品质相同,且只能整盒购买,商品信息如下:
A包装盒 B包装盒
每盒面包个数(个) 3 8
每盒价格(元) 5 11
若某同学正好买了50个面包,则他最少需要花( )元;
A.71 B.74 C.75 D.81
【考点5】古代问题;
9.我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有16头,下有44足,问鸡兔各几何.”设鸡x只,兔y只,可列方程组( )
A. B.
C. D.
10.《孙子算经》中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,木长多少尺?若设绳子长x尺,木长y尺,所列方程组正确的是( )
A. B.
C. D.
【考点6】几何图形问题.
11.如图,用12块相同的长方形地砖拼成一个长方形.设一块长方形地砖的长和宽分别为和,一块长方形地砖的面积为( )
A. B. C. D.
12.如图,由七个完全一样的小长方形组成大长方形,,大长方形的周长为( )
A. B. C. D.
二、填空题
【考点1】数字问题;
13.已知一个两位数,它的十位上的数字与个位上的数字之和为15,若对调个位与十位上的数字,得到的新数比原数小27,求这个两位数,设十位上的数字为x,个位上的数字为y,所列方程组(不用化简)为 .
14.“九宫图”又称“龟背图”,数学上的“九宫图”所体现的是一个表格,每一行的三个数、每一列的三个数、斜对角的三个数之和都相等,也称为三阶幻方.如图是一个满足条件的三阶幻方的一部分,则的值为 .
【考点2】年龄问题;
15.一名学生问老师:“你今年多大了?”老师风趣地说“我像你这样大的时候,你才2岁;你到我这么大时,我已经38岁了”,则今年老师的岁数是 .
16.甲对乙说:“当我的岁数是你现在的岁数时,你才4岁.”乙对甲说:“当我的岁数是你现在的岁数时,你将61岁.”则甲、乙现在的年龄分别是 .
【考点3】销售、利润问题;
17.某一天,蔬菜经营户王叔叔花270元从蔬菜批发市场批发了黄瓜和茄子共70千克,到菜市场按零售价卖,黄瓜和茄子当天的批发价和零售价如下表所示:
品名 黄瓜 茄子
批发价/(元/千克) 5 3
零售价/(元/千克) 7 4
他卖完这些黄瓜和茄子共赚了 元.
18.在当地农业技术部门的指导下,小明家种植的大棚油桃喜获丰收,去年大棚油桃的利润(利润=收入-支出)为12000元,今年大棚油桃的收入比去年增加了20%,支出减少了10%,预计今年的利润比去年多11400元,设小明家去年种植大棚油桃的收入为x元,支出是y元.依题意列方程组 .
【考点4】图表信息问题;
19.如图,在幻方中,填入个数字,使得每行、每列、每条对角线上的三个数之和都相等按以上规则填成的幻方中,的值为 .
20.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则 .
x 2y
y 6
0
【考点5】古代问题;
21.古代一歌谣:栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思是说,有一群乌鸦到树林休息,如果每棵树上有3只乌鸦,则有5只落在地上;如果每棵树上有5只乌鸦,则有一棵树上没有乌鸦,则共有 只乌鸦.
22.在《九章算术》中,一次方程组是由算筹布置而成的.图1所示的算筹图表示的是关于,的方程组,则图2所示的算筹图表示的方程组是 .
【考点6】几何图形问题.
23.如图,两根铁棒直立于桶底在水平面的木桶中,在桶中加入水后,一根露出水面的长度是它总长的,另一根露出水面的长度是它总长的.两根铁棒长度之和为,则两根铁棒的长度分别为 .
24.如图,长方形中放置9个形状,大小完全相同的小长方形,根据图中数据,求出图中阴影面积为 .
三、解答题
【考点1】数字问题;
25.一个两位数,十位上的数与个位上的数之和是8,个位数字与十位数字交换后所得新数比原数大.求这个两位数.
26.根据下列语句,分别设适当的未知数,列二元一次方程或方程组.
(1)甲数的比乙数的5倍大2;
(2)梯形的面积为,高是6cm,且下底比上底的2倍少1cm,求梯形上底和下底的长;
(3)如图,点C在直线上,的度数比的度数的3倍少,求和的度数.
【考点2】年龄问题;
27.5年前母亲的年龄是女儿年龄的15倍,15年后,母亲的年龄比女儿年龄的2倍多6岁.那么现在这对母女的年龄分别是多少?
28.10年前,小明妈妈的年龄是小明的6倍;10年后,小明妈妈的年龄将是小明的2倍.小明和他妈妈现在的年龄分别是多少?
【考点3】销售、利润问题;
29.某百货大楼购进商品后,加价作为销售价.五一黄金周快到了,商场搞优惠促销活动,决定A、B两种商品分别以折和折销售,某顾客购买A、B两种商品,共付款元.这两种商品原销售价之和为元,问这两种商品实际销售价格分别为多少元?
30.某海鲜排档购进一批大龙虾和海胆,它们的进货单价之和是360元.大龙虾零售单价比进货单价多40元,海胆零售单价比进货单价的1.5倍少60元,按零售单价购买大龙虾2只和海胆4个,共需要1200元.
(1)求大龙虾和海胆的进货单价;
(2)该海鲜排档平均每天卖出大龙虾20只和海胆12个.经调查发现,大龙虾零售单价每降低1元,平均每天就可多售出大龙虾2只,海鲜排档决定把大龙虾的零售单价下降元,海胆的零售单价和销量都不变,在不考虑其他因素的条件下,当a为多少时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元?
【考点4】图表信息问题;
31.某学校现有甲种材料,乙种材料,制作A,B两种型号的工艺品,用料情况如下表:
需甲种材料 需乙种材料
1件A型工艺品
1件B型工艺品
(1)利用这些材料能制作A,B两种型号的工艺品各多少件?
(2)若每千克甲、乙两种材料分别为8元和10元,问:制作A,B两种型号的工艺品各需材料费多少钱?
32.某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:若商场购进甲、乙两种型号的电视机共50台,用去9万元.
电视机型号 甲 乙
批发价(元/台) 1500 2500
零售价批发价(元/台) 2025 3640
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“国庆”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利,求甲种型号电视机打几折销售?
【考点5】古代问题;
33.《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣.其中下卷“雉兔同笼”流传尤为广泛.“雉兔同笼”题为:今有雉(鸡)兔同笼,上有三十五头,下有九十四足,问雉兔各几何?上述“雉兔同笼”问题中,鸡和兔各有多少只?
34.《九章算术》中记载:“今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?”意思是:今有人合伙买金,每人出钱400,会多出3400钱;每人出钱300,会多出100钱,问合伙人数、金价各是多少?
【考点6】几何图形问题.
35.列二元一次方程组解应用题:某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?
36.如图,这是某江滩公园正在修建的一运动场馆的规划示意图,运动场馆是一个长方形,长为120米,宽为90米,计划在甲、乙、丙三块形状及大小相同的小长方形地块上修建网球场,剩余两块形状及大小相同的空地铺设塑胶草坪,求每块草坪的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】设这首歌的歌词的字数的十位数字为x,个位数字为y,由题意:十位数字是个位数字的两倍,且十位数字比个位数字大4,列出二元一次方程组,解方程组即可.
【详解】解:设这个两位数的个位数是x,十位数是y.
根据题意,得
解得
则这首歌的歌词的字数是84个.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
2.C
【分析】设这个两位数为,依题意,则或,解方程组即可求解.
【详解】解:设这个两位数为,依题意,则或,
解得:或,
故选:C.
【点睛】本题考查了二元一次方程组的应用,根据题意列出方程组是解题的关键.
3.A
【分析】设老师现在的年龄是岁,学生现在的年龄是岁,抓住年龄差不变,根据此等量关系可列方程组求解.
【详解】解:设老师现在的年龄是岁,学生现在的年龄是岁,
由题意可得:,
解得:.
故老师现在的年龄是24岁,学生现在的年龄是12岁.
故选:A.
【点睛】本题考查了二元一次方程组的应用,关键是知道年龄差是不变的量从而可列方程求解.
4.C
【分析】根据题中已知量和未知量之间的等量关系,设未知数,列二元一次方程组即可解决.
【详解】解:设甲现在x岁,乙现在y岁.
根据题意,得,
解得,
∴
故选:C
【点睛】本题考查了列方程组解应用题的知识点,找出题中已知量和未知之间的等量关系是解题的关键.
5.A
【分析】
本题考查了二元一次方程组的应用,设,两种图书的单价分别为元,元,根据题意列出方程组,解方程组即可求解.
【详解】解:设,两种图书的单价分别为元,元,根据题意得,
解得:
即,两种图书的单价分别为10元、30元,
故选:A.
6.A
【分析】设成人票是元张,学生票是元张,根据“李凯同学一家个成人和个学生去了该景区,门票共花费元,王玲同学一家个成人和个学生去了该景区,门票共花费元”列出方程组,求得的值即可.
【详解】解:设成人票是元张,学生票是元张,
依题意得:
,
②①得:.
即赵芸同学和妈妈去该景区游玩时,门票需要花费元.
故选:A.
【点睛】本题考查了二元一次方程组的应用.此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为,另一个未知数用含的式子来表示,进而列并解方程即可.
7.C
【分析】本题考查了二元一次方程组的应用及求代数式的值,能根据题意列出方程组是解此题的关键.根据题意得出方程组,求出方程组的解,代入计算即可.
【详解】解:由题意得:,
解得:,
∴.
故选:C.
8.B
【分析】设购买A包装面包x盒,B包装面包y盒,由题意:某同学正好买了50个面包,结合表中信息列出二元一次方程,求出非负整数解,即可解决问题.
【详解】解:设购买A包装面包x盒,B包装面包y盒,
由题意得: 3x + 8y= 50,
∵x、y为非负整数
∴ 或 ,
∴当x=6,y= 8时,
费用为:5×6+11×4= 74(元);
当x= 14,y= 1时,费用为:5×14+11×1= 81(元);
∵74<81,
∴某同学正好买了50个面包,则他最少需要花74元
故选: B.
【点睛】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
9.A
【分析】本题考查了由实际问题抽象出二元一次方程组,解题的关键是找出等量关系.
设鸡x只,兔y只,根据上有16头,下有44足列出二元一次方程组即可.
【详解】设鸡x只,兔y只,
根据题意得,.
故选:A.
10.B
【分析】此题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程组是解答本题的关键.根据“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量木条,木头剩余1尺”,即可得出方程组即可.
【详解】解:∵用绳子去量长木,绳子还剩余4.5尺,
∴;
∵将绳子对折再量长木,长木还剩余1尺,
∴.
∴所列方程组为.
故选:B.
11.C
【分析】
本题主要考查了二元一次方程组的实际应用,设一块长方形地砖的长和宽分别为和,根据题意可知宽的两倍与长的和为,2个长与4个宽加一个长的长度相等,据此列出方程组求解即可.
【详解】解:由题意得,,
解得,
∴一块长方形地砖的面积为,
故选:C.
12.B
【分析】此题考查二元一次方程组的应用,正确的理解题意是解题的关键. 由图可看出本题的等量关系:小长方形的长小长方形的宽;小长方形的长+宽,据此可以列出方程组求解.
【详解】解:设小长方形的长为x,宽为y.
由图可知,
解得.
所以长方形的长为10,宽为7,
∴长方形的周长为,
故选B.
13.
【分析】本题考查二元一次方程组的应用,由“十位上的数字与个位上的数字之和为15”可得,这个两位数表示为,对调个位与十位上的数字表示为,根据“得到的新数比原数小27”可得方程“”,组成方程组即可.
【详解】解:根据“它的十位上的数字与个位上的数字之和为15,若对调个位与十位上的数字,得到的新数比原数小27”,
可得:
故答案为:.
14.17
【分析】根据三阶幻方的规则列出方程组求解x、y即可.
【详解】解:由题意,得,
解得,
∴,
故答案为:17.
【点睛】本题考查二元一次方程组的应用,理解题意,找出等量关系,正确列出方程组是解答的关键.
15.26
【分析】设今年老师的岁数是x岁,学生的岁数是y岁,根据学生今年年龄减年龄差等于2,老师今年年龄加年龄差等于38,列出二元一次方程组即可.
【详解】解:设今年老师的岁数是x岁,学生的岁数是y岁,
依题意得:,
解得:.
故答案为:26.
【点睛】本题考查二元一次方程组,设出恰当的未知数,准确抓住数量关系列出方程组是解题的关键.
16.42岁,23岁
【分析】设甲现在x岁,乙现在y岁,根据甲、乙年龄之间的关系,可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设甲现在x岁,乙现在y岁,
依题意,得:,
解得:.
答:甲现在42岁,乙现在23岁.
故答案为:42岁,23岁.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
17.100
【分析】
本题考查二元一次方程组的实际应用,设批发黄瓜千克,茄子千克,根据王叔叔花270元从蔬菜批发市场批发了黄瓜和茄子共70千克,列出方程组求出的值,再利用总利润等于单件利润乘以销量,求解即可.
【详解】解:设批发黄瓜千克,茄子千克,由题意,得:
,解得:,
∴(元);
故答案为:100.
18.
【分析】审题,明确等量关系,建立方程组.
【详解】解:由题意知,今年收入为,今年支出,故
故答案为:
【点睛】本题考查二元一次方程组的应用,根据题意明确等量关系是解题的关键.
19.
【分析】根据题意可知每行每列每对角线上的三个数之和都相等可知,即可得解;
【详解】∵每行每列每对角线上的三个数之和都相等,
∴,
解得,
故答案为:.
【点睛】本题考查了有理数的加法,二元一次方程的应用,根据表格,根据每行每列每对角线上的三个数之和都相等得知是解题的关键.
20.
【分析】根据图中各行、各列上的三个数之和都相等,即可得出关于x,y的二元一次方程组,求解后即可得出结果.
【详解】解:依题意得: ,
解得,
∴.
故答案为:.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
21.
【分析】本题考查二元一次方程组与实际问题.根据题意可设乌鸦有只,树有棵,然后列出方程组求解即可.
【详解】解:设乌鸦有只,树有棵,依题得
解得
故答案为:.
22.
【分析】
本题考查了由实际问题抽象出二元一次方程组以及数学常识,找准等量关系,正确列出二元一次方程组是解题的关键.
根据图1所表示方程组,可找出各算筹表示的数量:第一列表示x系数,第二列表示y系数,第三列表示常数项,进而可得出图2所表示的方程组
【详解】解:由题意,图2所示的算筹图表示的方程组是,
故答案为:.
23.,
【分析】本题主要考查了二元一次方程组的应用,解题的关键是设两根铁棒的长度分别为,,根据两根铁棒长度之和为,一根露出水面的长度是它总长的,另一根露出水面的长度是它总长的,列出方程组,解方程组即可.
【详解】解:设两根铁棒的长度分别为,,由题意得:
解得:,
故答案为:,.
24.18
【分析】本题考查了二元一次方程组的应用,设每个小长方形的长为x,宽为y,根据题意,得,结合计算即可.
【详解】设每个小长方形的长为x,宽为y,根据题意,得
,
解得
故,
故答案为:18.
25.这个两位数为
【分析】
本题考查了二元一次方程组的应用,设这个两位数的十位数字为x,个位数字为y.可列方程组求解.
【详解】解:设这个两位数的十位数字为x,个位数字为y.
依题意,得:
解得:
答:这个两位数为.
26.(1)
(2)
(3)
【详解】(1)设甲数为x,乙数为y,则.
(2)设梯形的上底为xcm,下底为ycm,则
(3)设和的度数分别为,,则
27.母亲现在年龄35岁,女儿现在7岁
【分析】设母亲现在年龄x岁,女儿现在y岁,然后根据5年前母亲的年龄是女儿年龄的15倍,15年后,母亲的年龄比女儿年龄的2倍多6岁,列出方程组求解即可.
【详解】解:设母亲现在年龄x岁,女儿现在y岁,则
解得
答:母亲现在年龄35岁,女儿现在7岁.
【点睛】本题主要考查了二元一次方程组的应用,解题的关键在于正确理解题意列出方程求解.
28.小明和他妈妈现在的年龄分别是15岁和40岁
【分析】根据题意,设小明和他妈妈现在的年龄分别是x岁和y岁,列二元一次方程组,解方程求解即可
【详解】设小明和他妈妈现在的年龄分别是x岁和y岁,根据题意,
得
解得
答:小明和他妈妈现在的年龄分别是15岁和40岁.
【点睛】本题考查了二元一次方程组的应用,根据题意列出方程组是解题的关键.
29.这两种商品实际销售价格分别为、元.
【分析】本题考查了二元一次方程组的应用,读懂题意,找出数量关系是解题关键.设这两种商品实际销售价格分别为、元,根据题意列二元一次方程组求解即可.
【详解】解:设这两种商品实际销售价格分别为、元,
由题意得:,
解得:,
答:这两种商品实际销售价格分别为、元.
30.(1)大龙虾进货单价为200元,海胆的进货单价为160元
(2)15
【分析】本题考查了一元二次方程的应用∶
(1)设大龙虾进货单价为x元,海胆的进货单价为y元,由它们的进货单价之和是360元和按零售单价购买大龙虾2只和海胆4个,共需要1200元,列出方程组,即可求解;
(2)由海鲜排档每天销售大龙虾和海胆获取的总利润为1490元,列出方程可求解.
【详解】(1)解:设大龙虾进货单价为x元,海胆的进货单价为y元,依题意有∶
,
解得:,
答:大龙虾进货单价为200元,海胆的进货单价为160元;
(2)依题意有,
解得.
故当a为15时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元.
31.(1)制作A种型号的工艺品30件,B种型号的工艺品20件
(2)306元,264元
【分析】
本题主要考查了二元一次方程组的应用,另外还涉及有理数混合运算的应用;
(1)设利用这些材料能制作A种型号的工艺品x件,B种型号的工艺品y件,根据等量关系:两种工艺品所需甲种材料为,两种工艺品所需乙种材料为,列出二元一次方程组,并求解即可;
(2)分别计算出制作1件两种型号的工艺品需要的费用,则可计算出制作A,B两种型号的工艺品各需材料费.
【详解】(1)解:设利用这些材料能制作A种型号的工艺品x件,B种型号的工艺品y件,
由题意,得,解得;
答:利用这些材料能制作A种型号的工艺品30件,B种型号的工艺品20件.
(2)解:制作1件A种型号的工艺品需要(元),
则制作A种型号的工艺品需材料费(元);
制作1件B种型号的工艺品需要(元),
则制作B种型号的工艺品需材料费(元).
答:制作A,B两种型号的工艺品各需材料费306元,264元.
32.(1)购进甲型号电视机35台,乙型号电视机15台
(2)8折
【分析】(1)设商场购进甲型号电视机台,乙型号电视机台,根据“商场购进甲、乙两种型号的电视机共50台,用去9万元”列出二元一次方程组,解方程组即可;
(2)设甲种型号电视机打折销售,根据“两种电视机销售完毕,商场共获利”列出一元一次方程,解方程即可.
【详解】(1)解:设商场购进甲型号电视机台,乙型号电视机台,
由题意得:,
解得:,
答:商场购进甲型号电视机35台,乙型号电视机15台;
(2)设甲种型号电视机打折销售,
由题意得:,
解得:,
答:甲种型号电视机打8折销售.
【点睛】本题考查了二元一次方程组和一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元一次方程.
33.鸡和兔各有23只,12只
【分析】本题主要考查了二元一次方程组的实际应用,设鸡有x只,兔有y只,根据共有三十五头可得方程,根据共有九十四足,可得方程,据此列出方程组求解即可.
【详解】解:设鸡有x只,兔有y只,
由题意得,,
解得,
答:鸡和兔各有23只,12只.
34.合伙人数是33人,金价是9800钱
【分析】
本题考查了二元一次方程组的应用以及数学常识.设共人合伙买金,金价为钱,根据“每人出400钱,会剩余3400钱;每人出300钱,会剩余100钱”,即可得出关于,的二元一次方程组,解之即可得出结论.
【详解】
解:设共人合伙买金,金价为钱,
依题意得:,
解得:.
答:共33人合伙买金,金价为9800钱.
35.预计花费75600元.
【分析】本题考查的是二元一次方程组的应用,根据长方形的性质列出方程组是解本题的关键.
设小长方形的长为米,宽为米,则根据长方形的性质可列方程组,再解方程组即可得到答案.
【详解】解:设小长方形的长为米,宽为米,
依题意得
解得
所以(元).
答:预计花费75600元.
36.3900平方米
【分析】本题考查了二元一次方程组的应用.三个小长方形的长为x米,宽为y米,根据题意,列出方程,可求出三个小长方形的总面积,再用大长方形的面积减去三个小长方形的总面积,即可求解.
【详解】解:设三个小长方形的长为x米,宽为y米,根据题意得:
,
解得:,
∴三个小长方形的总面积为平方米,
∴每块草坪的面积为平方米.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
