高中数学人教B版(2019)选择性必修第一册 第1章 1.1.2 空间向量基本定理 同步练习(含解析)
文档属性
| 名称 | 高中数学人教B版(2019)选择性必修第一册 第1章 1.1.2 空间向量基本定理 同步练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 717.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览




文档简介
人教B版(2019)数学高中选择性必修第一册
1.1.2 空间向量基本定理
一.选择题
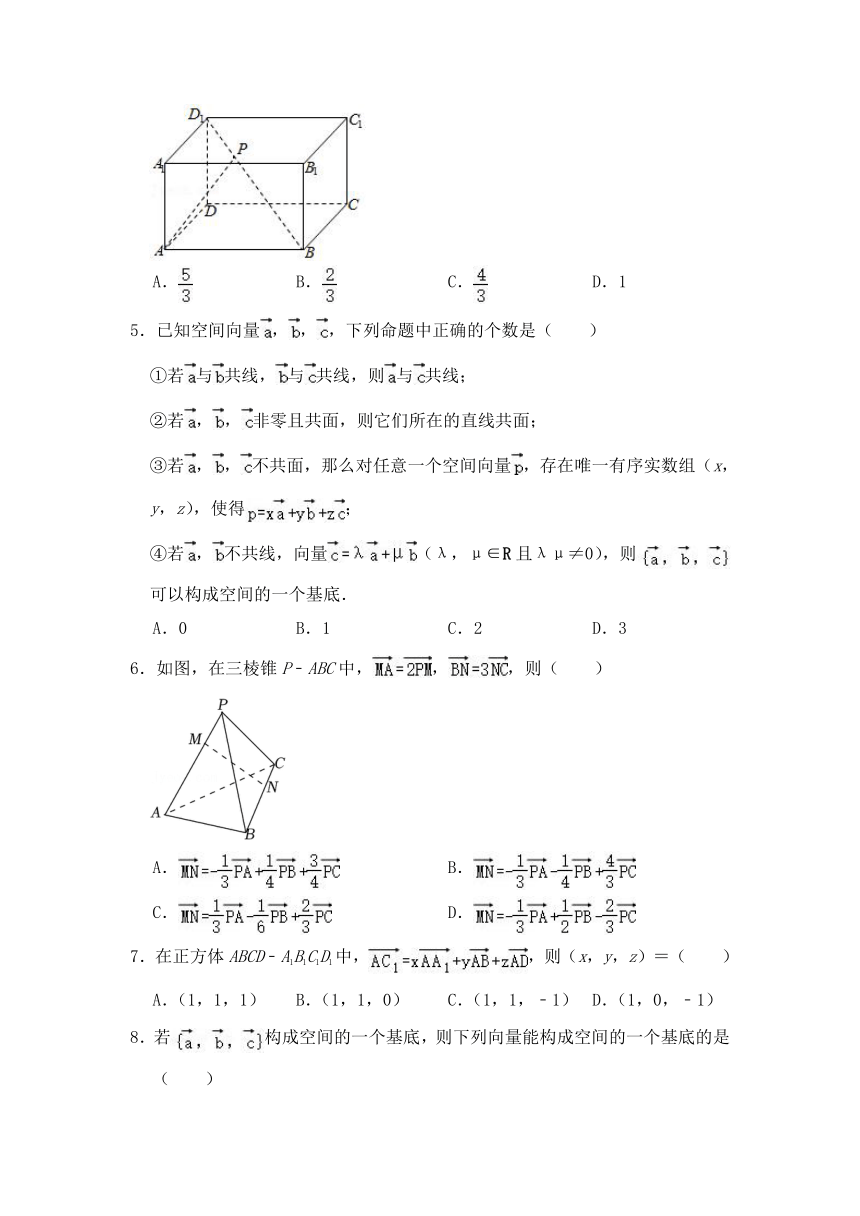
1.如图,在平行六面体ABCD﹣A1B1C1D1中,,,,则与向量相等的是( )
A. B. C. D.
2.《九章算术》中的“商功”篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵ABC﹣A1B1C1中,M,N分别是A1C1,BB1的中点,G是MN的中点,若=x+y+z,则x+y+z=( )
A.1 B. C. D.
3.在四面体O﹣ABC中,设=,=,=,=3,若F为BC的中点,P为EF的中点,则=( )
A.++ B.++ C.++ D.++
4.如图,在长方体ABCD﹣A1B1C1D1中,P是线段D1B上一点,且BP=2D1P,若=x+y+z,则x+y+z=( )
A. B. C. D.1
5.已知空间向量,,,下列命题中正确的个数是( )
①若与共线,与共线,则与共线;
②若,,非零且共面,则它们所在的直线共面;
③若,,不共面,那么对任意一个空间向量,存在唯一有序实数组(x,y,z),使得;
④若,不共线,向量(λ,μ∈R且λμ≠0),则可以构成空间的一个基底.
A.0 B.1 C.2 D.3
6.如图,在三棱锥P﹣ABC中,,,则( )
A. B.
C. D.
7.在正方体ABCD﹣A1B1C1D1中,,则(x,y,z)=( )
A.(1,1,1) B.(1,1,0) C.(1,1,﹣1) D.(1,0,﹣1)
8.若构成空间的一个基底,则下列向量能构成空间的一个基底的是( )
A.,, B.,, C.,, D.,,
9.已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且,,,则x+y+z=( )
A. B. C.1 D.
10.已知{,,}是空间的一个基底,{+,﹣,}是空间的另一个基底,一向量在基底{,,}下的坐标为(4,2,3),则向量在基底{+,﹣,}下的坐标是( )
A.(4,0,3) B.(3,1,3) C.(1,2,3) D.(2,1,3)
二.填空题
11.在平行六面体ABCD﹣A1B1C1D1中,用向量,,表示= .
12.如图所示,三棱柱ABC﹣A1B1C1中,M,N分别是A1B和B1C1上的点,且BM=3A1M,C1N=2B1N.设,则x+y+z的值为 .
13.已知向量,,可作为空间的一组基底{,,},若=3+4+,且在基底{(+2),(+3),(+)}下满足=x(+2)+y(+3)+z(+),则x= .
14.在长方体ABCD﹣A1B1C1D1中,若=3,=2,=5,则向量在基底{,,}下的坐标是 .
15.如图所示,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且AP=3PN,=,设,,则= (用来表示)
三.解答题
16.定义:设{,,}是空间的一个基底,若向量=x+y+z,则称有序实数组(x,y,z)为向量在基底{,,}下的坐标.
已知{,,}是空间的单位正交基底,{,﹣,}是空间的另一个基底,若向量在基底{,﹣,}下的坐标为(1,2,3).
(1)求向量在基底{,,}下的坐标;
(2)求向量的模.
17.对于任意空间四边形ABCD,E,F分别是AB,CD的中点.
(1)试证:与,共面;
(2)=,=,=,试用基底{,,}表示向量.
18.如图,在三棱锥P﹣ABC中,点G为△ABC的重心,点M在PG上,且PM=3MG,过点M任意作一个平面分别交线段PA,PB,PC于点D,E,F,若=m,=n,=t,求证:++为定值,并求出该定值.
人教B版(2019)数学高中选择性必修第一册
1.1.2 空间向量基本定理
参考答案与试题解析
一.选择题
1.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:根据题意,=+=++=+﹣=+﹣,
故选:A.
2.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:连接AM,AN,如下图:
由于G是MN的中点,
∴==,
根据题意知,
所以x+y+z=,
故选:C.
3.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:画出图形,如图所示,
则=+===
=+×=()
=.
故选:A.
4.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:∵BP=2D1P,
∴=2,
即﹣=2(﹣)=2﹣2,
即3=+2,
即,
所以,,,所以.
故选:A.
5.【考点】空间向量基本定理、正交分解及坐标表示;命题的真假判断与应用.
【解答】解:对于①,若与共线,与共线,则当时,与不共线,故①错误;
对于②,共面向量的定义是平行于同一平面的向量,
∴,,非零且共面,则表示这些向量的有向线段所在的直线不一定共面,故②错误;
对于③,由空间向量基本定理可知:
若,,不共面,那么对任意一个空间向量,存在唯一有序实数组(x,y,z),使得,故③正确;
④若,不共线,向量,
则共在,∴不可以构成空间的一个基底,故④错误.
故选:B.
6.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:∵,,
∴=++=+﹣+(﹣)
=﹣++,
故选:A.
7.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:∵正方体ABCD﹣A1B1C1D1,
∴=++=++,
∵,
∴(x,y,z)=(1,1,1),
故选:A.
8.【考点】空间向量基本定理、正交分解及坐标表示;平面向量的基本定理.
【解答】解:对于A,若向量,,共面,
则=,即,解得λ=﹣1,μ=2,
故向量,,共面,故A错误,
对于B,若向量,,共面,
则=,λ,μ无解,
故向量,,不共面,故B正确,
对于C,若向量,,共面,
则=,即,解得λ=2,μ=﹣1,
故向量,,共面,故C错误,
对于D,若向量,,共面,
则,解得λ=μ=1,
故向量,,共面,故D错误.
故选:B.
9.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:分别以AB、AD、AP为x、y、z轴,建立空间直角坐标系,如图所示:
设B=(a,0,0),D=(0,b,0),P=(0,0,C),
所以M=(a,b,c),N=(0,b,c),
所以=(a,b,﹣c)=+﹣,
所以x=,y=,z=﹣,
所以x+y+z=.
故选:B.
10.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:设向量在基底,{+,﹣,}下的坐标为(x,y,z),
则=4+2+3=x(+)+y(﹣)+z,
整理得:4+2+3=(x+y)+(x﹣y)+z,
∴,解得x=3,y=1,z=3,
∴向量在基底{+,﹣,}下的坐标是(3,1,3).
故选:B.
二.填空题
11.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:在平行六面体ABCD﹣A1B1C1D1中,
=++=.
故答案为:.
12.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:由题意三棱柱ABC﹣A1B1C1中,M、N分别是A1B、B1C1上的点,
且BM=3A1M,C1N=2B1N,
则=
=
=﹣
=,
∵,
∴x+y+z==1.
故答案为:1.
13.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:因为=3+4+,且=x(+2)+y(+3)+z(+)=(x+z)+(2x+y)+(3y+z),
则,
解得x=2,y=0,z=1.
故答案为:2.
14.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:在长方体ABCD﹣A1B1C1D1中,若=3,=2,=5,
则=.
故答案为:(3,2,5).
15.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:因为M是四面体OABC的棱BC的中点,所以=+,
因为=,
所以=+=+=+×(+)=﹣++,
因为AP=3PN,
所以==﹣++,
所以=+=﹣++=++.
故答案为:++.
三.解答题
16.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:向量在基底下的坐标为(1,2,3),则 ,
(1)所以向量在基底下的坐标为(6,﹣1,6),
(2)模为=.
17.【考点】空间向量基本定理、正交分解及坐标表示;共线向量与共面向量.
【解答】(1)证明:如图,连接AC,取AC的中点P,连接PE,PF.
∵P,F分别为AC,CD的中点,∴AD∥PF.
又∵PF 平面PEF,AD 平面PEF.
∴AD∥平面PEF.
同理可证,BC∥平面PEF.
∴向量与,共面;
(2)解:=
==.
18.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】证明:如图示:
连接AG并延长交BC于点H,
由题意可令{,,}为空间的一个基底,
故==(+)=+
=+ (+)=+(﹣)+(﹣)
=++,
连接DM,因为点D,E,F,M共面,
故存在实数λ,μ,使得=λ+μ,
即﹣=λ(﹣)+μ(﹣),
故=(1﹣λ﹣μ)+λ+μ=(1﹣λ﹣μ)m+λn+μt,
由空间向量基本定理知=(1﹣λ﹣μ)m,=λn,=μt,
故++=4(1﹣λ﹣μ)+4λ+4μ=4,为定值.
1.1.2 空间向量基本定理
一.选择题
1.如图,在平行六面体ABCD﹣A1B1C1D1中,,,,则与向量相等的是( )
A. B. C. D.
2.《九章算术》中的“商功”篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵ABC﹣A1B1C1中,M,N分别是A1C1,BB1的中点,G是MN的中点,若=x+y+z,则x+y+z=( )
A.1 B. C. D.
3.在四面体O﹣ABC中,设=,=,=,=3,若F为BC的中点,P为EF的中点,则=( )
A.++ B.++ C.++ D.++
4.如图,在长方体ABCD﹣A1B1C1D1中,P是线段D1B上一点,且BP=2D1P,若=x+y+z,则x+y+z=( )
A. B. C. D.1
5.已知空间向量,,,下列命题中正确的个数是( )
①若与共线,与共线,则与共线;
②若,,非零且共面,则它们所在的直线共面;
③若,,不共面,那么对任意一个空间向量,存在唯一有序实数组(x,y,z),使得;
④若,不共线,向量(λ,μ∈R且λμ≠0),则可以构成空间的一个基底.
A.0 B.1 C.2 D.3
6.如图,在三棱锥P﹣ABC中,,,则( )
A. B.
C. D.
7.在正方体ABCD﹣A1B1C1D1中,,则(x,y,z)=( )
A.(1,1,1) B.(1,1,0) C.(1,1,﹣1) D.(1,0,﹣1)
8.若构成空间的一个基底,则下列向量能构成空间的一个基底的是( )
A.,, B.,, C.,, D.,,
9.已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且,,,则x+y+z=( )
A. B. C.1 D.
10.已知{,,}是空间的一个基底,{+,﹣,}是空间的另一个基底,一向量在基底{,,}下的坐标为(4,2,3),则向量在基底{+,﹣,}下的坐标是( )
A.(4,0,3) B.(3,1,3) C.(1,2,3) D.(2,1,3)
二.填空题
11.在平行六面体ABCD﹣A1B1C1D1中,用向量,,表示= .
12.如图所示,三棱柱ABC﹣A1B1C1中,M,N分别是A1B和B1C1上的点,且BM=3A1M,C1N=2B1N.设,则x+y+z的值为 .
13.已知向量,,可作为空间的一组基底{,,},若=3+4+,且在基底{(+2),(+3),(+)}下满足=x(+2)+y(+3)+z(+),则x= .
14.在长方体ABCD﹣A1B1C1D1中,若=3,=2,=5,则向量在基底{,,}下的坐标是 .
15.如图所示,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且AP=3PN,=,设,,则= (用来表示)
三.解答题
16.定义:设{,,}是空间的一个基底,若向量=x+y+z,则称有序实数组(x,y,z)为向量在基底{,,}下的坐标.
已知{,,}是空间的单位正交基底,{,﹣,}是空间的另一个基底,若向量在基底{,﹣,}下的坐标为(1,2,3).
(1)求向量在基底{,,}下的坐标;
(2)求向量的模.
17.对于任意空间四边形ABCD,E,F分别是AB,CD的中点.
(1)试证:与,共面;
(2)=,=,=,试用基底{,,}表示向量.
18.如图,在三棱锥P﹣ABC中,点G为△ABC的重心,点M在PG上,且PM=3MG,过点M任意作一个平面分别交线段PA,PB,PC于点D,E,F,若=m,=n,=t,求证:++为定值,并求出该定值.
人教B版(2019)数学高中选择性必修第一册
1.1.2 空间向量基本定理
参考答案与试题解析
一.选择题
1.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:根据题意,=+=++=+﹣=+﹣,
故选:A.
2.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:连接AM,AN,如下图:
由于G是MN的中点,
∴==,
根据题意知,
所以x+y+z=,
故选:C.
3.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:画出图形,如图所示,
则=+===
=+×=()
=.
故选:A.
4.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:∵BP=2D1P,
∴=2,
即﹣=2(﹣)=2﹣2,
即3=+2,
即,
所以,,,所以.
故选:A.
5.【考点】空间向量基本定理、正交分解及坐标表示;命题的真假判断与应用.
【解答】解:对于①,若与共线,与共线,则当时,与不共线,故①错误;
对于②,共面向量的定义是平行于同一平面的向量,
∴,,非零且共面,则表示这些向量的有向线段所在的直线不一定共面,故②错误;
对于③,由空间向量基本定理可知:
若,,不共面,那么对任意一个空间向量,存在唯一有序实数组(x,y,z),使得,故③正确;
④若,不共线,向量,
则共在,∴不可以构成空间的一个基底,故④错误.
故选:B.
6.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:∵,,
∴=++=+﹣+(﹣)
=﹣++,
故选:A.
7.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:∵正方体ABCD﹣A1B1C1D1,
∴=++=++,
∵,
∴(x,y,z)=(1,1,1),
故选:A.
8.【考点】空间向量基本定理、正交分解及坐标表示;平面向量的基本定理.
【解答】解:对于A,若向量,,共面,
则=,即,解得λ=﹣1,μ=2,
故向量,,共面,故A错误,
对于B,若向量,,共面,
则=,λ,μ无解,
故向量,,不共面,故B正确,
对于C,若向量,,共面,
则=,即,解得λ=2,μ=﹣1,
故向量,,共面,故C错误,
对于D,若向量,,共面,
则,解得λ=μ=1,
故向量,,共面,故D错误.
故选:B.
9.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:分别以AB、AD、AP为x、y、z轴,建立空间直角坐标系,如图所示:
设B=(a,0,0),D=(0,b,0),P=(0,0,C),
所以M=(a,b,c),N=(0,b,c),
所以=(a,b,﹣c)=+﹣,
所以x=,y=,z=﹣,
所以x+y+z=.
故选:B.
10.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:设向量在基底,{+,﹣,}下的坐标为(x,y,z),
则=4+2+3=x(+)+y(﹣)+z,
整理得:4+2+3=(x+y)+(x﹣y)+z,
∴,解得x=3,y=1,z=3,
∴向量在基底{+,﹣,}下的坐标是(3,1,3).
故选:B.
二.填空题
11.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:在平行六面体ABCD﹣A1B1C1D1中,
=++=.
故答案为:.
12.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:由题意三棱柱ABC﹣A1B1C1中,M、N分别是A1B、B1C1上的点,
且BM=3A1M,C1N=2B1N,
则=
=
=﹣
=,
∵,
∴x+y+z==1.
故答案为:1.
13.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:因为=3+4+,且=x(+2)+y(+3)+z(+)=(x+z)+(2x+y)+(3y+z),
则,
解得x=2,y=0,z=1.
故答案为:2.
14.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:在长方体ABCD﹣A1B1C1D1中,若=3,=2,=5,
则=.
故答案为:(3,2,5).
15.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:因为M是四面体OABC的棱BC的中点,所以=+,
因为=,
所以=+=+=+×(+)=﹣++,
因为AP=3PN,
所以==﹣++,
所以=+=﹣++=++.
故答案为:++.
三.解答题
16.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】解:向量在基底下的坐标为(1,2,3),则 ,
(1)所以向量在基底下的坐标为(6,﹣1,6),
(2)模为=.
17.【考点】空间向量基本定理、正交分解及坐标表示;共线向量与共面向量.
【解答】(1)证明:如图,连接AC,取AC的中点P,连接PE,PF.
∵P,F分别为AC,CD的中点,∴AD∥PF.
又∵PF 平面PEF,AD 平面PEF.
∴AD∥平面PEF.
同理可证,BC∥平面PEF.
∴向量与,共面;
(2)解:=
==.
18.【考点】空间向量基本定理、正交分解及坐标表示.
【解答】证明:如图示:
连接AG并延长交BC于点H,
由题意可令{,,}为空间的一个基底,
故==(+)=+
=+ (+)=+(﹣)+(﹣)
=++,
连接DM,因为点D,E,F,M共面,
故存在实数λ,μ,使得=λ+μ,
即﹣=λ(﹣)+μ(﹣),
故=(1﹣λ﹣μ)+λ+μ=(1﹣λ﹣μ)m+λn+μt,
由空间向量基本定理知=(1﹣λ﹣μ)m,=λn,=μt,
故++=4(1﹣λ﹣μ)+4λ+4μ=4,为定值.
