高中数学人教B版(2019)选择性必修第一册 第1章 1.2.5 空间中的距离 同步练习(含解析)
文档属性
| 名称 | 高中数学人教B版(2019)选择性必修第一册 第1章 1.2.5 空间中的距离 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 542.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览




文档简介
人教B版(2019)数学高中选择性必修第一册
1.2.5 空间中的距离
一.选择题
1.已知空间向量=(2,3,6),=(3,﹣4,1),则<,>=( )
A. B. C. D.
2.已知空间向量=(1,﹣1,0),=(1,﹣1,1),则|+|=( )
A.3 B. C. D.
3.已知斜三棱柱ABC﹣A1B1C1所有棱长均为2,,点E、F满足,,则=( )
A. B. C.2 D.
4.已知,,且,则向量与的夹角为( )
A. B. C. D.
5.在空间直角坐标系O﹣xyz中,点A(3,4,5)在坐标平面Oxy,Oxz内的射影分别为点B,C,则=( )
A.5 B. C. D.
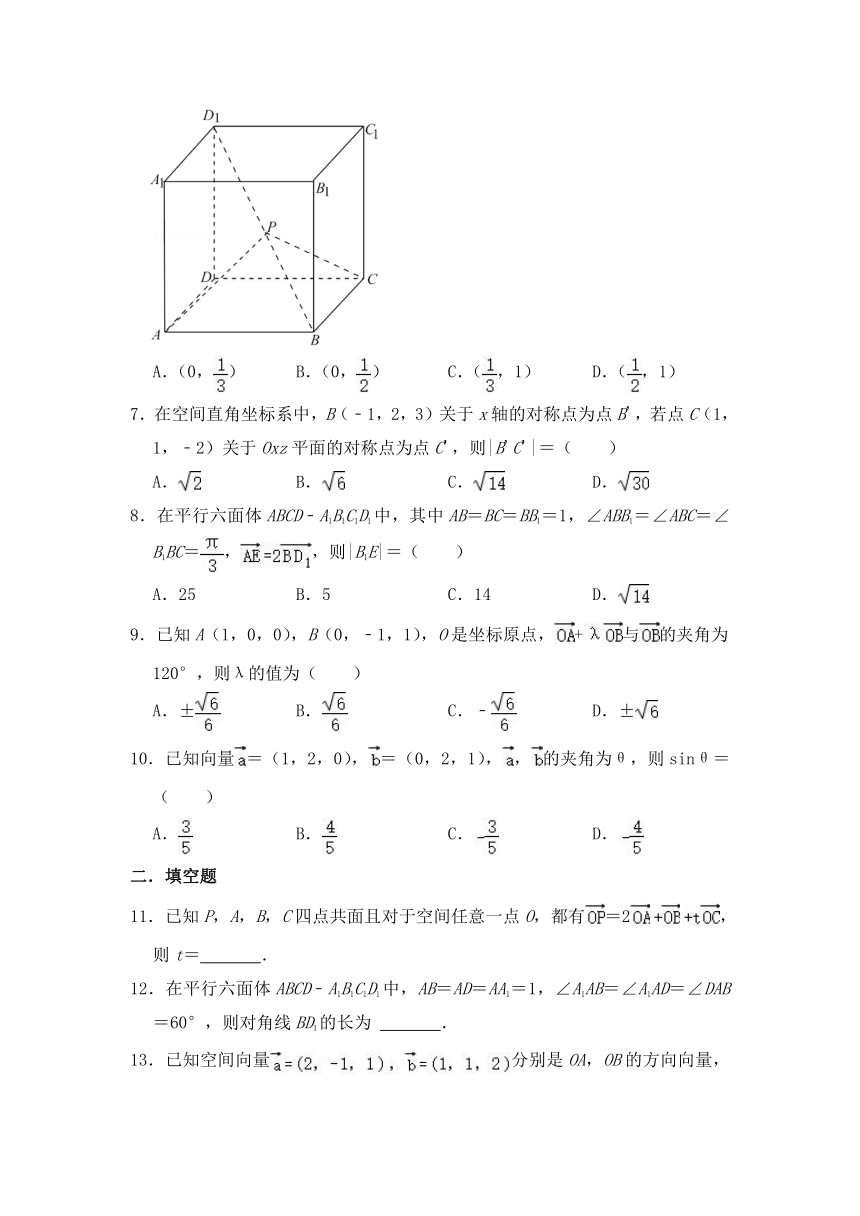
6.已知动点P在正方体ABCD﹣A1B1C1D1的对角线BD1(不含端点)上.设=λ,若∠APC为钝角,则实数λ的取值范围为( )
A.(0,) B.(0,) C.(,1) D.(,1)
7.在空间直角坐标系中,B(﹣1,2,3)关于x轴的对称点为点B',若点C(1,1,﹣2)关于Oxz平面的对称点为点C',则|B'C'|=( )
A. B. C. D.
8.在平行六面体ABCD﹣A1B1C1D1中,其中AB=BC=BB1=1,∠ABB1=∠ABC=∠B1BC=,,则|B1E|=( )
A.25 B.5 C.14 D.
9.已知A(1,0,0),B(0,﹣1,1),O是坐标原点,+与的夹角为120°,则λ的值为( )
A.± B. C.﹣ D.±
10.已知向量=(1,2,0),=(0,2,1),,的夹角为θ,则sinθ=( )
A. B. C. D.
二.填空题
11.已知P,A,B,C四点共面且对于空间任意一点O,都有=2,则t= .
12.在平行六面体ABCD﹣A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠DAB=60°,则对角线BD1的长为 .
13.已知空间向量分别是OA,OB的方向向量,则= ;向量与的夹角为 .
14.若,,则的值为 .
15.将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足=﹣+,则||的值为 .
三.解答题
16.已知:=(x,4,1),=(﹣2,y,﹣1),=(3,﹣2,z),∥,⊥,求:
(1),,;
(2)+与+所成角的余弦值.
17.已知=(1,1,0),=(﹣1,0,2),
(1)求|2|;
(2)若k与2的夹角为钝角,求实数k的取值范围.
18.如图,直三棱柱ABC﹣A1B1C1底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M是A1B1的中点.
(1)求cos<,>的值;
(2)求证:A1B⊥C1M.
人教B版(2019)数学高中选择性必修第一册
1.2.5 空间中的距离
参考答案与试题解析
一.选择题
1.【考点】空间向量的夹角与距离求解公式;空间向量的数量积运算.
【解答】解:∵空间向量=(2,3,6),=(3,﹣4,1),
∴cos<>==0,则<,>=.
故选:A.
2.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵空间向量=(1,﹣1,0),=(1,﹣1,1),
∴=(2,﹣2,1),
|+|==3.
故选:A.
3.【考点】空间向量的夹角与距离求解公式.
【解答】解:=++=+(﹣)﹣=+﹣,
∵斜三棱柱ABC﹣A1B1C1所有棱长均为2,,
点E、F满足,,
∴=+++ ﹣ ﹣
=1+1+1+×2×2×﹣2×1×﹣2×1×=2,
∴=,
故选:D.
4.【考点】空间向量的夹角与距离求解公式.
【解答】解:,,且,
可得x﹣2=﹣3,解得x=﹣1,
向量与的夹角为θ,cosθ==﹣,θ∈[0,π],
所以θ=.
故选:A.
5.【考点】空间向量的夹角与距离求解公式.
【解答】解:在空间直角坐标系O﹣xyz中,点A(3,4,5)在坐标平面Oxy,Oxz内的射影分别为点B,C,
则B(3,4,0),C(3,0,5),
∴=(0,﹣4,5),
∴||==.
故选:C.
6.【考点】空间向量的夹角与距离求解公式.
【解答】解:由题设,建立如图所示的空间直角坐标系D﹣xyz,
设正方体ABCD﹣A1B1C1D1的棱长为1,
则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1)
∴=(1,1,﹣1),∴设=(λ,λ,﹣λ),
∴==(﹣λ,﹣λ,λ)+(1,0,﹣1)=(1﹣λ,﹣λ,λ﹣1),
=+=(﹣λ,﹣λ,λ)+(0,1,﹣1)=(﹣λ,1﹣λ,λ﹣1),
由图知∠APC不是平角,∴∠APC为钝角等价于cos∠APC<0,
∴<0,
∴(1﹣λ)(﹣λ)+(﹣λ)(1﹣λ)+(λ﹣1)2=(λ﹣1)(3λ﹣1)<0,
解得<λ<1,
∴λ的取值范围是(,1).
故选:C.
7.【考点】空间向量的夹角与距离求解公式.
【解答】解:空间直角坐标系中,B(﹣1,2,3)关于x轴的对称点为点B'(﹣1,﹣2,﹣3),
点C(1,1,﹣2)关于Oxz平面的对称点为点C'(1,﹣1,﹣2),
所以|B'C'|==.
故选:B.
8.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵在平行六面体ABCD﹣A1B1C1D1中,其中AB=BC=BB1=1,
∠ABB1=∠ABC=∠B1BC=,,
∴==
=+2()
=,
∴=()2=4+9++2|2| |3|cos60°+2|| ||cos60°+2|3| ||cos60°
=4+9+1+6+2+3
=25,
∴|B1E|=||==5.
故选:B.
9.【考点】空间向量的夹角与距离求解公式.
【解答】解:因为+λ=(1,0,0)+λ(0,﹣1,1)=(1,﹣λ,λ),
所以=,
=,
(+λ) =2λ,
所以cos 120°==﹣,
所以λ<0,
且4λ=﹣,
解得:λ=﹣.
故选:C.
10.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵向量=(1,2,0),=(0,2,1),,的夹角为θ,
∴cosθ===,
∴sinθ===.
故选:A.
二.填空题
11.【考点】空间向量的夹角与距离求解公式.
【解答】解:=﹣=,=﹣=2,=﹣=2,
∵P,A,B,C四点共面,∴存在m,n∈R使得=m+n,
∴=m(2)+n[2]=(2m+2n)+n+(mt+nt﹣n),
∴,解得m=﹣,n=1,t=﹣2.
故答案为:﹣2.
12.【考点】空间向量的夹角与距离求解公式.
【解答】解:如图,=,
∴2=()2
=+2|| || cos60°+2|| ||cos120°+2|| || cos120°
=1+1+1+1﹣1﹣1
=2,
∴对角线BD1的长为.
故答案为:.
13.【考点】空间向量的夹角与距离求解公式;平面向量数量积的坐标表示、模、夹角.
【解答】解:根据题意,空间向量,
则+=(3,0,3),则|+|==3,
=2×1+(﹣1)×1+1×2=3,||==,||==,
则cos<,>==,
又由0°≤<,>≤180°,则<,>=60°,
故答案为:3,60°.
14.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵,,
∴,
∴=.
故答案为:5.
15.【考点】空间向量的夹角与距离求解公式.
【解答】解:分别取BC,BA,AD,BD的中点E,F,G,O,连接EF、FG、EG、AO、CO,
则AO⊥BD,CO⊥BD,EF∥AC,GF∥BD,
∵边长为1的正方形ABCD沿对角线BD折成直二面角,
∴BD==,AC===1,
∴EF=AC=,
∵AO∩CO=O,∴BD⊥平面AOC,∵AC 平面AOC,
∴AC⊥BD,∴EF⊥FG,∴,
=﹣+=++=+=,
∴||===.
故答案为:.
三.解答题
16.【考点】空间向量的夹角与距离求解公式;向量的数量积判断向量的共线与垂直.
【解答】解:(1)∵,
∴,
解得x=2,y=﹣4,
故=(2,4,1),=(﹣2,﹣4,﹣1),
又因为,所以=0,即﹣6+8﹣z=0,解得z=2,
故=(3,﹣2,2);
(2)由(1)可得=(5,2,3),=(1,﹣6,1),
设向量与所成的角为θ,
则cosθ==.
17.【考点】空间向量的夹角与距离求解公式.
【解答】解:(1)=(1,1,0),=(﹣1,0,2),
∴=(3,2,﹣2),
∴|2|==;
(2)k=(k﹣1,k,2),2=(3,2,﹣2),
∴(k) (2)=3k﹣3+2k﹣4=5k﹣7,
∵k与2的夹角为钝角,
∴(k) (2)=5k﹣7<0,且k≠﹣2,
解得k<,且k≠﹣2,
∴实数k的取值范围是(﹣∞,﹣2)∪(﹣2,).
18.【考点】空间向量的夹角与距离求解公式.
【解答】解:(1)以C为原点,CA,CB,CC1所在直线分别为x,y,z轴,建立空间直角坐标系,
A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),
=(1,﹣1,2),=(0,1,2),
∴cos<,>===.
证明:(2)A1(1,0,2),B(0,1,0),C1(0,0,2),M(),
=(﹣1,1,﹣2),=(,0),
=0,
∴A1B⊥C1M.
1.2.5 空间中的距离
一.选择题
1.已知空间向量=(2,3,6),=(3,﹣4,1),则<,>=( )
A. B. C. D.
2.已知空间向量=(1,﹣1,0),=(1,﹣1,1),则|+|=( )
A.3 B. C. D.
3.已知斜三棱柱ABC﹣A1B1C1所有棱长均为2,,点E、F满足,,则=( )
A. B. C.2 D.
4.已知,,且,则向量与的夹角为( )
A. B. C. D.
5.在空间直角坐标系O﹣xyz中,点A(3,4,5)在坐标平面Oxy,Oxz内的射影分别为点B,C,则=( )
A.5 B. C. D.
6.已知动点P在正方体ABCD﹣A1B1C1D1的对角线BD1(不含端点)上.设=λ,若∠APC为钝角,则实数λ的取值范围为( )
A.(0,) B.(0,) C.(,1) D.(,1)
7.在空间直角坐标系中,B(﹣1,2,3)关于x轴的对称点为点B',若点C(1,1,﹣2)关于Oxz平面的对称点为点C',则|B'C'|=( )
A. B. C. D.
8.在平行六面体ABCD﹣A1B1C1D1中,其中AB=BC=BB1=1,∠ABB1=∠ABC=∠B1BC=,,则|B1E|=( )
A.25 B.5 C.14 D.
9.已知A(1,0,0),B(0,﹣1,1),O是坐标原点,+与的夹角为120°,则λ的值为( )
A.± B. C.﹣ D.±
10.已知向量=(1,2,0),=(0,2,1),,的夹角为θ,则sinθ=( )
A. B. C. D.
二.填空题
11.已知P,A,B,C四点共面且对于空间任意一点O,都有=2,则t= .
12.在平行六面体ABCD﹣A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠DAB=60°,则对角线BD1的长为 .
13.已知空间向量分别是OA,OB的方向向量,则= ;向量与的夹角为 .
14.若,,则的值为 .
15.将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足=﹣+,则||的值为 .
三.解答题
16.已知:=(x,4,1),=(﹣2,y,﹣1),=(3,﹣2,z),∥,⊥,求:
(1),,;
(2)+与+所成角的余弦值.
17.已知=(1,1,0),=(﹣1,0,2),
(1)求|2|;
(2)若k与2的夹角为钝角,求实数k的取值范围.
18.如图,直三棱柱ABC﹣A1B1C1底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M是A1B1的中点.
(1)求cos<,>的值;
(2)求证:A1B⊥C1M.
人教B版(2019)数学高中选择性必修第一册
1.2.5 空间中的距离
参考答案与试题解析
一.选择题
1.【考点】空间向量的夹角与距离求解公式;空间向量的数量积运算.
【解答】解:∵空间向量=(2,3,6),=(3,﹣4,1),
∴cos<>==0,则<,>=.
故选:A.
2.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵空间向量=(1,﹣1,0),=(1,﹣1,1),
∴=(2,﹣2,1),
|+|==3.
故选:A.
3.【考点】空间向量的夹角与距离求解公式.
【解答】解:=++=+(﹣)﹣=+﹣,
∵斜三棱柱ABC﹣A1B1C1所有棱长均为2,,
点E、F满足,,
∴=+++ ﹣ ﹣
=1+1+1+×2×2×﹣2×1×﹣2×1×=2,
∴=,
故选:D.
4.【考点】空间向量的夹角与距离求解公式.
【解答】解:,,且,
可得x﹣2=﹣3,解得x=﹣1,
向量与的夹角为θ,cosθ==﹣,θ∈[0,π],
所以θ=.
故选:A.
5.【考点】空间向量的夹角与距离求解公式.
【解答】解:在空间直角坐标系O﹣xyz中,点A(3,4,5)在坐标平面Oxy,Oxz内的射影分别为点B,C,
则B(3,4,0),C(3,0,5),
∴=(0,﹣4,5),
∴||==.
故选:C.
6.【考点】空间向量的夹角与距离求解公式.
【解答】解:由题设,建立如图所示的空间直角坐标系D﹣xyz,
设正方体ABCD﹣A1B1C1D1的棱长为1,
则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1)
∴=(1,1,﹣1),∴设=(λ,λ,﹣λ),
∴==(﹣λ,﹣λ,λ)+(1,0,﹣1)=(1﹣λ,﹣λ,λ﹣1),
=+=(﹣λ,﹣λ,λ)+(0,1,﹣1)=(﹣λ,1﹣λ,λ﹣1),
由图知∠APC不是平角,∴∠APC为钝角等价于cos∠APC<0,
∴<0,
∴(1﹣λ)(﹣λ)+(﹣λ)(1﹣λ)+(λ﹣1)2=(λ﹣1)(3λ﹣1)<0,
解得<λ<1,
∴λ的取值范围是(,1).
故选:C.
7.【考点】空间向量的夹角与距离求解公式.
【解答】解:空间直角坐标系中,B(﹣1,2,3)关于x轴的对称点为点B'(﹣1,﹣2,﹣3),
点C(1,1,﹣2)关于Oxz平面的对称点为点C'(1,﹣1,﹣2),
所以|B'C'|==.
故选:B.
8.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵在平行六面体ABCD﹣A1B1C1D1中,其中AB=BC=BB1=1,
∠ABB1=∠ABC=∠B1BC=,,
∴==
=+2()
=,
∴=()2=4+9++2|2| |3|cos60°+2|| ||cos60°+2|3| ||cos60°
=4+9+1+6+2+3
=25,
∴|B1E|=||==5.
故选:B.
9.【考点】空间向量的夹角与距离求解公式.
【解答】解:因为+λ=(1,0,0)+λ(0,﹣1,1)=(1,﹣λ,λ),
所以=,
=,
(+λ) =2λ,
所以cos 120°==﹣,
所以λ<0,
且4λ=﹣,
解得:λ=﹣.
故选:C.
10.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵向量=(1,2,0),=(0,2,1),,的夹角为θ,
∴cosθ===,
∴sinθ===.
故选:A.
二.填空题
11.【考点】空间向量的夹角与距离求解公式.
【解答】解:=﹣=,=﹣=2,=﹣=2,
∵P,A,B,C四点共面,∴存在m,n∈R使得=m+n,
∴=m(2)+n[2]=(2m+2n)+n+(mt+nt﹣n),
∴,解得m=﹣,n=1,t=﹣2.
故答案为:﹣2.
12.【考点】空间向量的夹角与距离求解公式.
【解答】解:如图,=,
∴2=()2
=+2|| || cos60°+2|| ||cos120°+2|| || cos120°
=1+1+1+1﹣1﹣1
=2,
∴对角线BD1的长为.
故答案为:.
13.【考点】空间向量的夹角与距离求解公式;平面向量数量积的坐标表示、模、夹角.
【解答】解:根据题意,空间向量,
则+=(3,0,3),则|+|==3,
=2×1+(﹣1)×1+1×2=3,||==,||==,
则cos<,>==,
又由0°≤<,>≤180°,则<,>=60°,
故答案为:3,60°.
14.【考点】空间向量的夹角与距离求解公式.
【解答】解:∵,,
∴,
∴=.
故答案为:5.
15.【考点】空间向量的夹角与距离求解公式.
【解答】解:分别取BC,BA,AD,BD的中点E,F,G,O,连接EF、FG、EG、AO、CO,
则AO⊥BD,CO⊥BD,EF∥AC,GF∥BD,
∵边长为1的正方形ABCD沿对角线BD折成直二面角,
∴BD==,AC===1,
∴EF=AC=,
∵AO∩CO=O,∴BD⊥平面AOC,∵AC 平面AOC,
∴AC⊥BD,∴EF⊥FG,∴,
=﹣+=++=+=,
∴||===.
故答案为:.
三.解答题
16.【考点】空间向量的夹角与距离求解公式;向量的数量积判断向量的共线与垂直.
【解答】解:(1)∵,
∴,
解得x=2,y=﹣4,
故=(2,4,1),=(﹣2,﹣4,﹣1),
又因为,所以=0,即﹣6+8﹣z=0,解得z=2,
故=(3,﹣2,2);
(2)由(1)可得=(5,2,3),=(1,﹣6,1),
设向量与所成的角为θ,
则cosθ==.
17.【考点】空间向量的夹角与距离求解公式.
【解答】解:(1)=(1,1,0),=(﹣1,0,2),
∴=(3,2,﹣2),
∴|2|==;
(2)k=(k﹣1,k,2),2=(3,2,﹣2),
∴(k) (2)=3k﹣3+2k﹣4=5k﹣7,
∵k与2的夹角为钝角,
∴(k) (2)=5k﹣7<0,且k≠﹣2,
解得k<,且k≠﹣2,
∴实数k的取值范围是(﹣∞,﹣2)∪(﹣2,).
18.【考点】空间向量的夹角与距离求解公式.
【解答】解:(1)以C为原点,CA,CB,CC1所在直线分别为x,y,z轴,建立空间直角坐标系,
A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),
=(1,﹣1,2),=(0,1,2),
∴cos<,>===.
证明:(2)A1(1,0,2),B(0,1,0),C1(0,0,2),M(),
=(﹣1,1,﹣2),=(,0),
=0,
∴A1B⊥C1M.
