1.2.1盖斯定律课件(共20张PPT)人教版(2019)选择性必修1
文档属性
| 名称 | 1.2.1盖斯定律课件(共20张PPT)人教版(2019)选择性必修1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2024-04-15 00:17:29 | ||
图片预览






文档简介
(共20张PPT)
课时1
盖斯定律
第二节 反应热的计算
01
学习目标
CONTENT
盖斯定律的意义
02
盖斯定律的应用
03
典例分析
中和热
在25℃和101kPa下,
_________跟_______的______溶液发生中和反应生成_____________时所释放的热量为 57.3 kJ。
强酸
强碱
稀
1mol水
中和热
定义:101 kPa时,1 mol纯物质完全燃烧生成指定产物时所放出的热量,叫做该物质的燃烧热,单位为kJ/mol。
碳元素变为CO2(g) 、氢元素变为H2O(l)、
硫 元素变为SO2(g)、氮元素变为N2(g)等 。
CO(g) + O2(g) CO2(g) H= 283 kJ/mol
1
2
2CO(g) + O2(g) 2CO2(g) H= 566 kJ/mol
燃烧热
可燃物的化学计量数为“1”
下列数据△H1表示燃烧热吗?Why?
提供: H2O(g)=H2O(l) △H2=-44kJ/mol
H2(g)+1/2O2(g)=H2O(g) △H1= -241.8kJ/mol
H2(g)+1/2O2(g)=H2O(l)
△H=
那么,H2的燃烧热△H究竟是多少 如何计算
这是什么规律?
△H1+△H2
= - 285.8kJ/mol
H2SO4 H2SO4·H2O H2SO4·2H2O H2SO4·3H2O
G.H.Hess, 1802-1850
ΔH=ΔH1+ΔH2+ΔH3
ΔH1
ΔH2
ΔH3
化学家盖斯测量了许多化学反应的热效应。通过大量实验,盖斯发现:
ΔH
一个化学反应,不管是一步完成的还是分几步完成的,其反应热是相同的。即:在一定条件下,化学反应的反应热只与反应体系的始态和终态有关,而与反应进行的途径无关。
盖斯定律
反应热研究
反应热
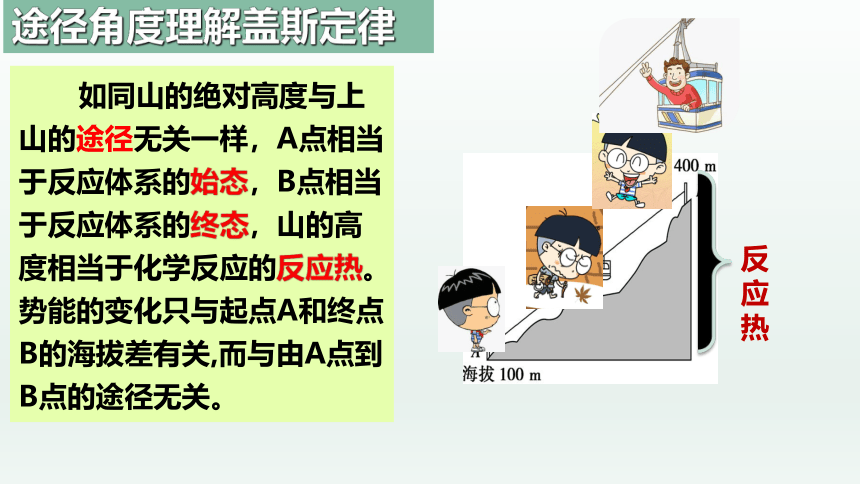
如同山的绝对高度与上山的途径无关一样,A点相当于反应体系的始态,B点相当于反应体系的终态,山的高度相当于化学反应的反应热。势能的变化只与起点A和终点B的海拔差有关,而与由A点到B点的途径无关。
途径角度理解盖斯定律
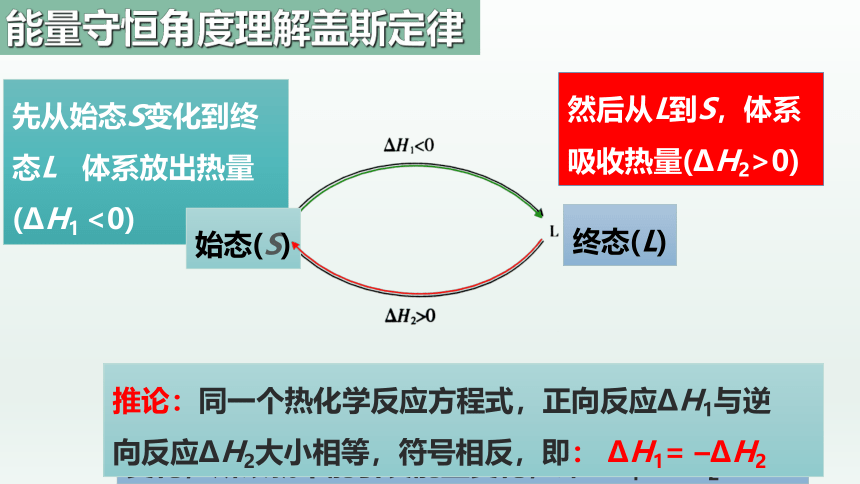
经过一个循环,体系仍处于S态,因为物质没有发生变化,所以就不能引发能量变化,即 H1+ H2=0
先从始态S变化到终态L 体系放出热量( H1 <0)
始态(S)
然后从L到S,体系吸收热量( H2>0)
终态(L)
推论:同一个热化学反应方程式,正向反应 H1与逆
向反应 H2大小相等,符号相反,即: H1= – H2
能量守恒角度理解盖斯定律
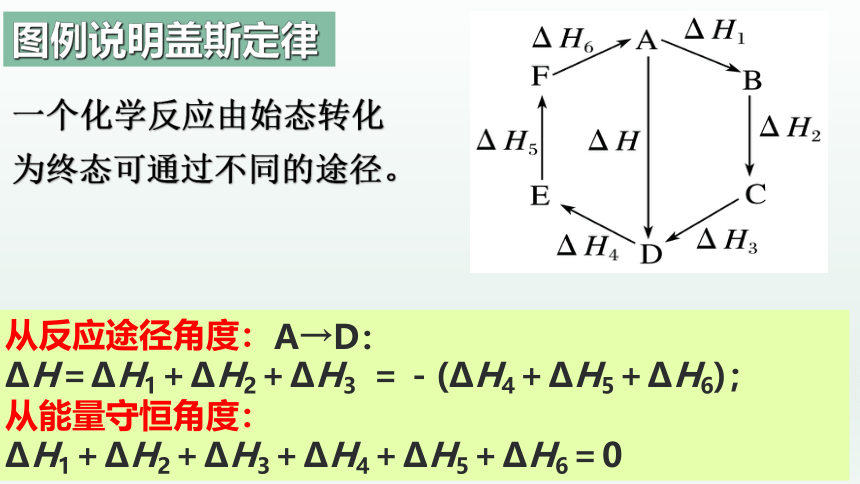
从反应途径角度:
ΔH=ΔH1+ΔH2+ΔH3 =-(ΔH4+ΔH5+ΔH6);
从能量守恒角度:
ΔH1+ΔH2+ΔH3+ΔH4+ΔH5+ΔH6=0
图例说明盖斯定律
一个化学反应由始态转化为终态可通过不同的途径。
A→D:
不能很好的控制反应的程度,故不能直接通过实验测得△H1
①C(s)+1/2O2(g)==CO(g) ΔH1=
②CO(g)+1/2O2(g)== CO2(g) ΔH2=-283.0kJ/mol
③C(s)+O2(g)==CO2(g) ΔH3=-393.5kJ/mol
如何测出下列反应的反应热:
C(s)+1/2O2(g)==CO(g) ΔH1=
【思考与讨论】
C(s)+ O2(g)
CO2(g)
△H1
△H3
△H1= △H2 + △H3
CO(g) + O2(g)
1
2
△H2
△H3 =△H1 - △H2
C(s)+1/2O2(g) = CO(g) △H1=?
物质 燃烧热
ΔH (kJ/mol)
C(s) 393.5
CO(g) 283.0
思路1:虚拟路径法
路径I
路径II
= 393.5 kJ/mol ( 283.0 kJ/mol)
= 110.5 kJ/mol
盖斯定律的应用
C(s) + O2(g) = CO(g) △H3=?
CO(g)+ O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s) + O2(g) = CO2(g) △H1=-393.5 kJ/mol
+)
△H3 =△H1 - △H2
= -393.5 kJ/mol -(-283.0 kJ/mol= -110.5 kJ/mol
1
2
1
2
C(s) + O2(g) = CO(g) △H3= -110.5 kJ/mol
1
2
即运用所给热化学方程式通过加减的方法得到所求热化学方程式。
思路2:加合法
查燃烧热表知:
①C(石墨,s)+O2(g)= CO2(g) △H1=-393.5kJ/mol
②C(金刚石,s)+O2(g)= CO2(g) △H2=-395.0kJ/mol
解:①- ②得:C(石墨,s)= C(金刚石,s) ; △H=+1.5kJ/mol
写出石墨变成金刚石的热化学方程式 (25℃,101kPa时)
根据盖斯定律书写热化学方程式的方法:
(1)确定待求反应的热化学方程式;
(2)找出待求热化学方程式中各物质出现在已知方程式中的位置(是同侧还是异侧);
(3)利用同侧相加、异侧相减进行处理;
(4)分析目标方程式中各物质的化学计量数,通过乘除来调整已知反应的化学计量数,并消去中间产物;
(5)实施叠加并确定反应热的变化。
① CO(g) + 1/2 O2(g) = CO2(g) ; ΔH1= -283.0 kJ/mol
② H2(g) + 1/2 O2(g) = H2O(l) ; ΔH2= -285.8 kJ/mol
③ C2H5OH(l) + 3 O2(g) = 2 CO2(g) + 3H2O(l); ΔH3=-1370 kJ/mol
试计算: ④ 2CO(g)+ 4 H2(g) = H2O(l)+ C2H5OH (l) 的ΔH
【解】:①×2 + ②×4 - ③ = ④
ΔH=ΔH1×2 +ΔH2×4 -ΔH3
=-283.2×2 -285.8×4 +1370 =-339.2 kJ/mol
【课堂练习】
1、热化学方程式同乘以一个数时,反应热数值也必须同乘以该数值;
2、热化学方程式相加减时,同种物质之间可相加减,反应热也随之相加减;
3、将一个热化学方程式颠倒, △H的符号也要随之改变
盖斯定律的小规则
同素异形体相互转化的反应热相当小,而且转化速率较慢,有时还很不完全,测定反应热很困难。现在可根据盖斯定律来计算反应热。
已知 P4(s,白磷)+5O2(g)=P4O10(s) ΔH =-2 983.2 kJ·mol-1①
4P(s,红磷)+5O2(g)=P4O10(s) ΔH=-2954 kJ·mol-1②
则白磷转化为红磷的热化学方程式为
_ ___________________________________________________________;
相同状况下,能量状态较低的是________;白磷的稳定性比红磷______(填“高”或“低”)。
P4(s,白磷)=4P(s,红磷) ΔH=-29.2 kJ·mol-1
红磷
低
【课堂练习】
1.实验中不能直接测出由石墨和氢气生成甲烷反应的ΔH,但可测出CH4燃烧反应的ΔH1,根据盖斯定律求ΔH4 。
CH4(g)+2O2(g)=CO2(g)+2H2O(l) ΔH1=-890.3kJ·mol-1 ①
C(石墨)+O2(g)=CO2(g) ΔH2=-393·5kJ·mol-1 ②
H2(g)+ O2(g)=H2O(l) ΔH3=-285.8kJ·mol-1 ③
C(石墨)+2H2(g)=CH4(g) ΔH4 ④
ΔH4 =-74.8kJ·mol-1
-① + ② + ③ ×2= ④
【课堂练习】
①H2O(g)=H2O(l) ΔH1=Q1 kJ·mol-1
②C2H5OH(g)=C2H5OH(l) ΔH2=Q2 kJ·mol-1
③C2H5OH(g)+3O2(g)=2CO2(g)+3H2O(g)
ΔH3=Q3 kJ·mol-1
则反应C2H5OH(l)+3O2(g)=2CO2(g)+3H2O(l)的反应热ΔH为( )
A.(Q1+Q2+Q3) kJ·mol-1 B.(3Q1+Q2+Q3) kJ·mol-1
C.(Q1-3Q2+Q3) kJ·mol-1 D.(3Q1-Q2+Q3) kJ·mol-1
典例分析
D
3.已知胆矾溶于水时溶液温度降低,胆矾分解的热化学方程式为CuSO4 5H2O(s) = CuSO4(s)+5H2O(l) △H=+Q1kJ/mol
室温下,若将1mol无水硫酸铜溶解为溶液 时放热Q2kJ,则( )
A.Q1>Q2 B.Q1=Q2 C.Q1A
△H=Q1+(-Q2)>0
【课堂练习】
理解与证明
课时1
盖斯定律
第二节 反应热的计算
01
学习目标
CONTENT
盖斯定律的意义
02
盖斯定律的应用
03
典例分析
中和热
在25℃和101kPa下,
_________跟_______的______溶液发生中和反应生成_____________时所释放的热量为 57.3 kJ。
强酸
强碱
稀
1mol水
中和热
定义:101 kPa时,1 mol纯物质完全燃烧生成指定产物时所放出的热量,叫做该物质的燃烧热,单位为kJ/mol。
碳元素变为CO2(g) 、氢元素变为H2O(l)、
硫 元素变为SO2(g)、氮元素变为N2(g)等 。
CO(g) + O2(g) CO2(g) H= 283 kJ/mol
1
2
2CO(g) + O2(g) 2CO2(g) H= 566 kJ/mol
燃烧热
可燃物的化学计量数为“1”
下列数据△H1表示燃烧热吗?Why?
提供: H2O(g)=H2O(l) △H2=-44kJ/mol
H2(g)+1/2O2(g)=H2O(g) △H1= -241.8kJ/mol
H2(g)+1/2O2(g)=H2O(l)
△H=
那么,H2的燃烧热△H究竟是多少 如何计算
这是什么规律?
△H1+△H2
= - 285.8kJ/mol
H2SO4 H2SO4·H2O H2SO4·2H2O H2SO4·3H2O
G.H.Hess, 1802-1850
ΔH=ΔH1+ΔH2+ΔH3
ΔH1
ΔH2
ΔH3
化学家盖斯测量了许多化学反应的热效应。通过大量实验,盖斯发现:
ΔH
一个化学反应,不管是一步完成的还是分几步完成的,其反应热是相同的。即:在一定条件下,化学反应的反应热只与反应体系的始态和终态有关,而与反应进行的途径无关。
盖斯定律
反应热研究
反应热
如同山的绝对高度与上山的途径无关一样,A点相当于反应体系的始态,B点相当于反应体系的终态,山的高度相当于化学反应的反应热。势能的变化只与起点A和终点B的海拔差有关,而与由A点到B点的途径无关。
途径角度理解盖斯定律
经过一个循环,体系仍处于S态,因为物质没有发生变化,所以就不能引发能量变化,即 H1+ H2=0
先从始态S变化到终态L 体系放出热量( H1 <0)
始态(S)
然后从L到S,体系吸收热量( H2>0)
终态(L)
推论:同一个热化学反应方程式,正向反应 H1与逆
向反应 H2大小相等,符号相反,即: H1= – H2
能量守恒角度理解盖斯定律
从反应途径角度:
ΔH=ΔH1+ΔH2+ΔH3 =-(ΔH4+ΔH5+ΔH6);
从能量守恒角度:
ΔH1+ΔH2+ΔH3+ΔH4+ΔH5+ΔH6=0
图例说明盖斯定律
一个化学反应由始态转化为终态可通过不同的途径。
A→D:
不能很好的控制反应的程度,故不能直接通过实验测得△H1
①C(s)+1/2O2(g)==CO(g) ΔH1=
②CO(g)+1/2O2(g)== CO2(g) ΔH2=-283.0kJ/mol
③C(s)+O2(g)==CO2(g) ΔH3=-393.5kJ/mol
如何测出下列反应的反应热:
C(s)+1/2O2(g)==CO(g) ΔH1=
【思考与讨论】
C(s)+ O2(g)
CO2(g)
△H1
△H3
△H1= △H2 + △H3
CO(g) + O2(g)
1
2
△H2
△H3 =△H1 - △H2
C(s)+1/2O2(g) = CO(g) △H1=?
物质 燃烧热
ΔH (kJ/mol)
C(s) 393.5
CO(g) 283.0
思路1:虚拟路径法
路径I
路径II
= 393.5 kJ/mol ( 283.0 kJ/mol)
= 110.5 kJ/mol
盖斯定律的应用
C(s) + O2(g) = CO(g) △H3=?
CO(g)+ O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s) + O2(g) = CO2(g) △H1=-393.5 kJ/mol
+)
△H3 =△H1 - △H2
= -393.5 kJ/mol -(-283.0 kJ/mol= -110.5 kJ/mol
1
2
1
2
C(s) + O2(g) = CO(g) △H3= -110.5 kJ/mol
1
2
即运用所给热化学方程式通过加减的方法得到所求热化学方程式。
思路2:加合法
查燃烧热表知:
①C(石墨,s)+O2(g)= CO2(g) △H1=-393.5kJ/mol
②C(金刚石,s)+O2(g)= CO2(g) △H2=-395.0kJ/mol
解:①- ②得:C(石墨,s)= C(金刚石,s) ; △H=+1.5kJ/mol
写出石墨变成金刚石的热化学方程式 (25℃,101kPa时)
根据盖斯定律书写热化学方程式的方法:
(1)确定待求反应的热化学方程式;
(2)找出待求热化学方程式中各物质出现在已知方程式中的位置(是同侧还是异侧);
(3)利用同侧相加、异侧相减进行处理;
(4)分析目标方程式中各物质的化学计量数,通过乘除来调整已知反应的化学计量数,并消去中间产物;
(5)实施叠加并确定反应热的变化。
① CO(g) + 1/2 O2(g) = CO2(g) ; ΔH1= -283.0 kJ/mol
② H2(g) + 1/2 O2(g) = H2O(l) ; ΔH2= -285.8 kJ/mol
③ C2H5OH(l) + 3 O2(g) = 2 CO2(g) + 3H2O(l); ΔH3=-1370 kJ/mol
试计算: ④ 2CO(g)+ 4 H2(g) = H2O(l)+ C2H5OH (l) 的ΔH
【解】:①×2 + ②×4 - ③ = ④
ΔH=ΔH1×2 +ΔH2×4 -ΔH3
=-283.2×2 -285.8×4 +1370 =-339.2 kJ/mol
【课堂练习】
1、热化学方程式同乘以一个数时,反应热数值也必须同乘以该数值;
2、热化学方程式相加减时,同种物质之间可相加减,反应热也随之相加减;
3、将一个热化学方程式颠倒, △H的符号也要随之改变
盖斯定律的小规则
同素异形体相互转化的反应热相当小,而且转化速率较慢,有时还很不完全,测定反应热很困难。现在可根据盖斯定律来计算反应热。
已知 P4(s,白磷)+5O2(g)=P4O10(s) ΔH =-2 983.2 kJ·mol-1①
4P(s,红磷)+5O2(g)=P4O10(s) ΔH=-2954 kJ·mol-1②
则白磷转化为红磷的热化学方程式为
_ ___________________________________________________________;
相同状况下,能量状态较低的是________;白磷的稳定性比红磷______(填“高”或“低”)。
P4(s,白磷)=4P(s,红磷) ΔH=-29.2 kJ·mol-1
红磷
低
【课堂练习】
1.实验中不能直接测出由石墨和氢气生成甲烷反应的ΔH,但可测出CH4燃烧反应的ΔH1,根据盖斯定律求ΔH4 。
CH4(g)+2O2(g)=CO2(g)+2H2O(l) ΔH1=-890.3kJ·mol-1 ①
C(石墨)+O2(g)=CO2(g) ΔH2=-393·5kJ·mol-1 ②
H2(g)+ O2(g)=H2O(l) ΔH3=-285.8kJ·mol-1 ③
C(石墨)+2H2(g)=CH4(g) ΔH4 ④
ΔH4 =-74.8kJ·mol-1
-① + ② + ③ ×2= ④
【课堂练习】
①H2O(g)=H2O(l) ΔH1=Q1 kJ·mol-1
②C2H5OH(g)=C2H5OH(l) ΔH2=Q2 kJ·mol-1
③C2H5OH(g)+3O2(g)=2CO2(g)+3H2O(g)
ΔH3=Q3 kJ·mol-1
则反应C2H5OH(l)+3O2(g)=2CO2(g)+3H2O(l)的反应热ΔH为( )
A.(Q1+Q2+Q3) kJ·mol-1 B.(3Q1+Q2+Q3) kJ·mol-1
C.(Q1-3Q2+Q3) kJ·mol-1 D.(3Q1-Q2+Q3) kJ·mol-1
典例分析
D
3.已知胆矾溶于水时溶液温度降低,胆矾分解的热化学方程式为CuSO4 5H2O(s) = CuSO4(s)+5H2O(l) △H=+Q1kJ/mol
室温下,若将1mol无水硫酸铜溶解为溶液 时放热Q2kJ,则( )
A.Q1>Q2 B.Q1=Q2 C.Q1
△H=Q1+(-Q2)>0
【课堂练习】
理解与证明
