初中数学苏科版九年级下册 7.1 正切 课件(共20张PPT)
文档属性
| 名称 | 初中数学苏科版九年级下册 7.1 正切 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 11:29:27 | ||
图片预览




文档简介
(共20张PPT)
7.1 正切
单击此处添加副标题
同学们,你们知道今天的日期吗?
你们知道古人是如何确定日期的吗?
01
单击此处添加标题
单击此处添加文本具体内容
02
单击此处添加标题
单击此处添加文本具体内容
一、创设情境
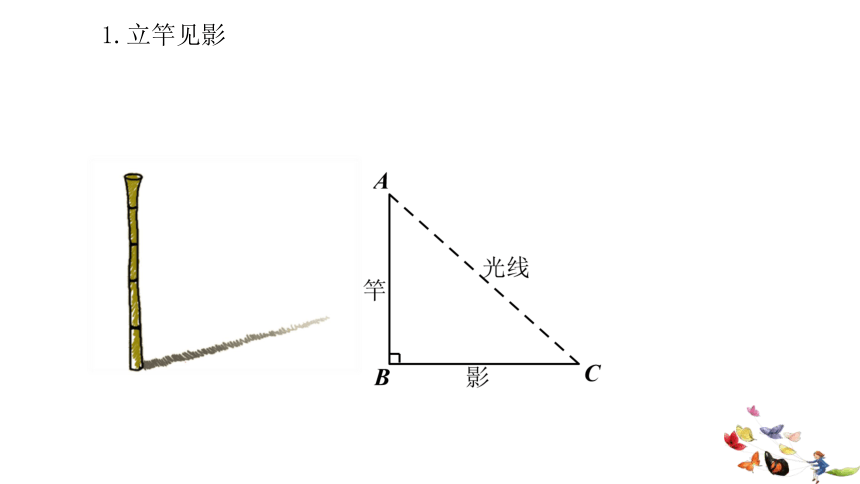
1.立竿见影
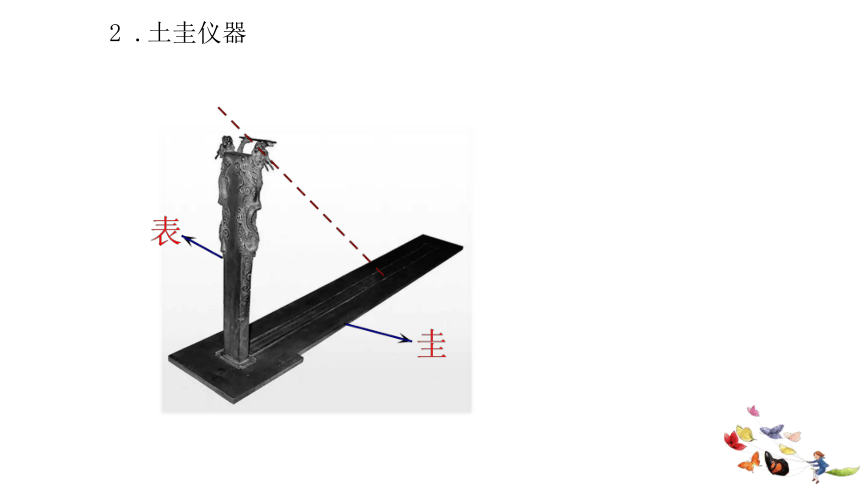
2 .土圭仪器
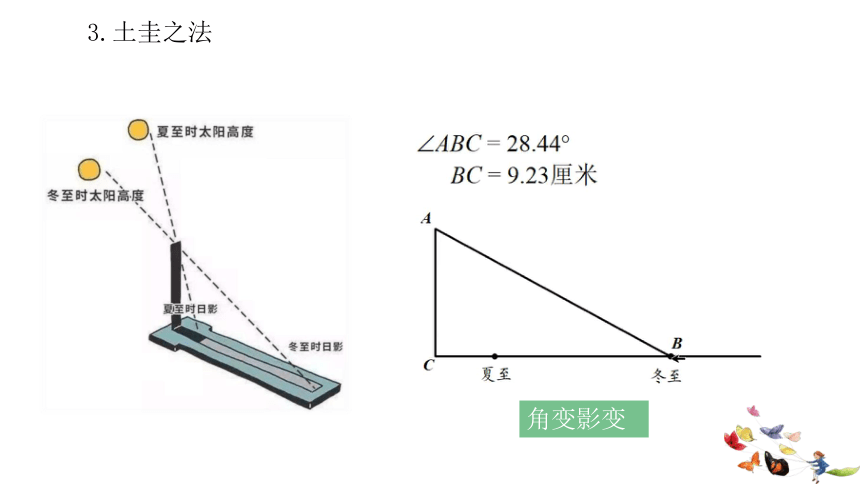
角变影变
3.土圭之法
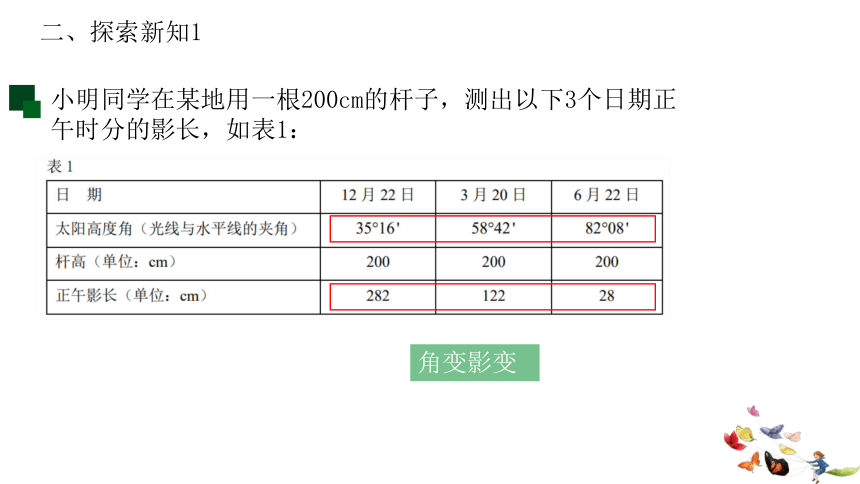
小明同学在某地用一根200cm的杆子,测出以下3个日期正午时分的影长,如表1:
角变影变
二、探索新知1
小明、小丽和小红三位同学分别使用200cm、100cm和50cm
的竿子,于12月22日这天正午时分在某地测得一组数据,如表2:
角定比定
二、探索新知2
如图, ∠A的大小确定
二、探索新知2
角定比定
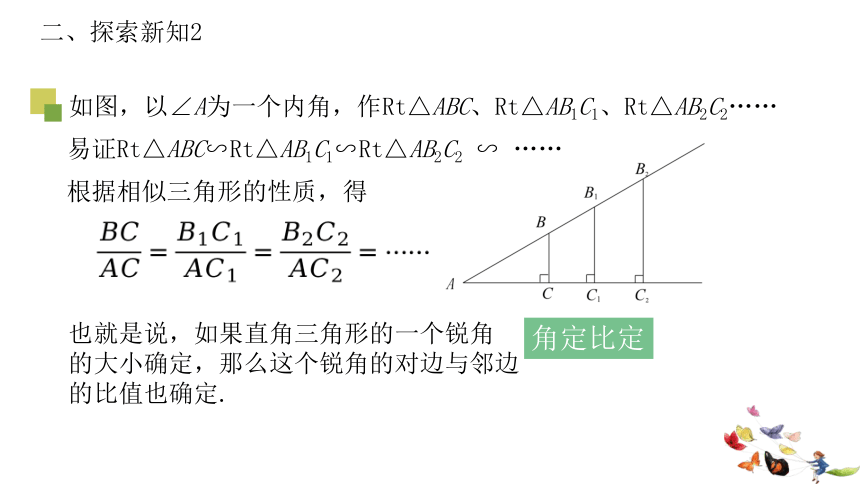
如图,以∠A为一个内角,作Rt△ABC、Rt△AB1C1、Rt△AB2C2……
易证Rt△ABC∽Rt△AB1C1∽Rt△AB2C2 ∽ ……
根据相似三角形的性质,得
也就是说,如果直角三角形的一个锐角
的大小确定,那么这个锐角的对边与邻边
的比值也确定.
二、探索新知2
小明、小丽和小红三位同学分别使用200cm、100cm和50cm的竿子,在同一地方测出以下3个日期正午时分的影长,如表3:
角变比变
二、探索新知3
如图,在Rt△ABC中,∠C=90°.
我们把∠A的对边a与邻边b的比叫做∠A的正切(tangent),
tanA=.
记作tan A ,即
三、归纳概念
下列说法正确的是( )
A.在Rt△ABC中,∠C=90°,若tanA= ,则BC=3,AC=4
B.在△ABC中,若BC=3,AC=4,则tanA=
C.在Rt△ABC中,∠C=90°,若BC和AC都扩大10倍,
则tanA也扩大10倍
D.在Rt△ABC中,∠C=90°, tanA tanB =1
四、概念辨析
X
缺少直角
X
比值
X
比值不变
tanA tanB =
D
.
五、史海拾贝
问题1 下表是我国唐代天文学家一行(公元683-727年)制作的正切表(部分).
.
五、以史为鉴
解:如图,作Rt△ABC,∠C=90°,∠A=45°,∠B=∠A=45°,
所以AC=BC,
tan45°=
.
例1 求45 °角的正切值.
六、典例精析
答:45°角的正切值为1.
古今对照,你有什么发现?
.
六、典例精析
1古度约为0.9856度
解:如图,作Rt△ABC,∠C=90°,∠A=30°,设BC=k,则AB=2 k,在Rt△ABC中,
根据勾股定理,得
同理可求,
六、典例精析
例2 求30 °、60 °角的正切值.
k
2k
将上面求得的正切函数值填入下表
六、典例精析
基础知识、基本技能
基本思想方法、基本活动经验
7.1 正切(1)
控制变量法、
数形结合思想、
函数思想、
定性研究-定量研究、
观察-猜想-证明
在Rt△ABC中,若∠C=90°,tanA =
tan30°=,tan45°=1,tan60° =.
抽象能力、
运算能力、
推理能力…
六、课堂小结
古人的智慧
同学们再见
单击此处添加副标题
7.1 正切
单击此处添加副标题
同学们,你们知道今天的日期吗?
你们知道古人是如何确定日期的吗?
01
单击此处添加标题
单击此处添加文本具体内容
02
单击此处添加标题
单击此处添加文本具体内容
一、创设情境
1.立竿见影
2 .土圭仪器
角变影变
3.土圭之法
小明同学在某地用一根200cm的杆子,测出以下3个日期正午时分的影长,如表1:
角变影变
二、探索新知1
小明、小丽和小红三位同学分别使用200cm、100cm和50cm
的竿子,于12月22日这天正午时分在某地测得一组数据,如表2:
角定比定
二、探索新知2
如图, ∠A的大小确定
二、探索新知2
角定比定
如图,以∠A为一个内角,作Rt△ABC、Rt△AB1C1、Rt△AB2C2……
易证Rt△ABC∽Rt△AB1C1∽Rt△AB2C2 ∽ ……
根据相似三角形的性质,得
也就是说,如果直角三角形的一个锐角
的大小确定,那么这个锐角的对边与邻边
的比值也确定.
二、探索新知2
小明、小丽和小红三位同学分别使用200cm、100cm和50cm的竿子,在同一地方测出以下3个日期正午时分的影长,如表3:
角变比变
二、探索新知3
如图,在Rt△ABC中,∠C=90°.
我们把∠A的对边a与邻边b的比叫做∠A的正切(tangent),
tanA=.
记作tan A ,即
三、归纳概念
下列说法正确的是( )
A.在Rt△ABC中,∠C=90°,若tanA= ,则BC=3,AC=4
B.在△ABC中,若BC=3,AC=4,则tanA=
C.在Rt△ABC中,∠C=90°,若BC和AC都扩大10倍,
则tanA也扩大10倍
D.在Rt△ABC中,∠C=90°, tanA tanB =1
四、概念辨析
X
缺少直角
X
比值
X
比值不变
tanA tanB =
D
.
五、史海拾贝
问题1 下表是我国唐代天文学家一行(公元683-727年)制作的正切表(部分).
.
五、以史为鉴
解:如图,作Rt△ABC,∠C=90°,∠A=45°,∠B=∠A=45°,
所以AC=BC,
tan45°=
.
例1 求45 °角的正切值.
六、典例精析
答:45°角的正切值为1.
古今对照,你有什么发现?
.
六、典例精析
1古度约为0.9856度
解:如图,作Rt△ABC,∠C=90°,∠A=30°,设BC=k,则AB=2 k,在Rt△ABC中,
根据勾股定理,得
同理可求,
六、典例精析
例2 求30 °、60 °角的正切值.
k
2k
将上面求得的正切函数值填入下表
六、典例精析
基础知识、基本技能
基本思想方法、基本活动经验
7.1 正切(1)
控制变量法、
数形结合思想、
函数思想、
定性研究-定量研究、
观察-猜想-证明
在Rt△ABC中,若∠C=90°,tanA =
tan30°=,tan45°=1,tan60° =.
抽象能力、
运算能力、
推理能力…
六、课堂小结
古人的智慧
同学们再见
单击此处添加副标题
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
